基于模式分离的兰姆波逆时偏移成像∗

张海燕 杨杰 范国鹏 朱文发 柴晓冬

1)(上海大学通信与信息工程学院,上海 200444)

2)(上海工程技术大学城市轨道交通学院,上海 201620)

基于模式分离的兰姆波逆时偏移成像∗

张海燕1)†杨杰1)范国鹏1)朱文发1)2)柴晓冬2)

1)(上海大学通信与信息工程学院,上海 200444)

2)(上海工程技术大学城市轨道交通学院,上海 201620)

(2017年5月31日收到;2017年6月30日收到修改稿)

兰姆波,逆时偏移,环形阵列,模式分离

1 引 言

超声波具有长距离传播特性和无损优势,由此应运而生的超声波地震勘探叠前偏移技术,近年来在地球物理勘探领域已经得到广泛应用.基于此,研究者又将该技术推广到工程结构的缺陷识别和健康监测领域[1].超声叠前偏移技术可检测板材结构表面或埋藏缺陷,对于小尺寸缺陷的检测可通过提高激励信号频率来实现[2].然而,一方面,传感器接收到的超声波信号存在较大分散性和随机性;另一方面,各向异性材料中多缺陷的散射信号相互影响的复杂机理导致计算量大,从而限制了叠前偏移检测技术的运用.常规叠前偏移技术已越来越难以满足业界需求,逆时偏移(reverse time migration,RTM)技术应运而生[3−10].

RTM的思想最早由Whitemore[3]提出.随后,RTM成像技术广泛应用于生物医学工程、工业无损检测、地球物理等领域.Arnal等[4]利用RTM对超声刀(HIFU)治疗的组织弹性硬度变化进行横波成像.Anderson等[5]提出基于RTM和时间反转[6]相结合的方法,由激发源产生声波,在感兴趣区域用激光测振仪接收波形,并利用时间反转镜将接收波形反转发射,激光测振仪再次接收信号,将两次接收信号进行互相关算法成像,成功定位出了铝板中的缺陷位置.Müller等[7]采用RTM方法仿真计算圆孔缺陷及台阶结构的声传播,并获得圆孔轮廓和台阶图像.马方正等[8]基于有限差分解微分方程,运用最小二乘技术进行反偏移数据重构,为岩性储层估计提供更加保真的、高分辨率反射系数成像.

目前国内外在RTM领域的研究工作主要集中在基于波动方程的逆时延拓算法和偏移成像条件两个方面.Lin和Yuan[9]将地震勘探领域中已经比较成熟的偏移方法引入到基于板中导波的损伤识别中,给出了板中低阶曲波模态A0波的控制方程.通过在板上均匀布置的传感器阵列依次激发和接收信号,并采用偏移法叠加对板材中不同形状单缺陷进行了成像.但是,这种偏移法叠加只利用了包含损伤信息的散射信号,未利用入射场的相关信息,致损伤成像精度较低.郑莉和郭建中[10]将线形阵元改进为圆环形阵元,并利用相控阵原理设计由径向振动的圆环形阵元组成的换能器阵列,在三维空间中构建了圆环形聚焦声场.

由于模式转换,兰姆波散射信号中一般包含多个模式的混叠,直接对其进行RTM成像必定会出现伪像[11].因此,首先对散射信号进行模式分离预处理,提取出单模态信号,再进行RTM成像,消除其他模态信号产生的伪像.采用频率域RTM方法,应用格林函数正向传播激励信号得到监测区域声场信息,反向传播时间反转后的散射信号得到监测区域声场信息,两次传播的声场信息互相关处理后成像,提高缺陷重构精度.为充分利用缺陷的全方位散射信息,采用环形阵列,全角度获取缺陷的散射信号,优化缺陷重建效果.

2 频域RTM理论

RTM,顾名思义,即逆时延拓和偏移的操作.其中,偏移是指计算机处理反演的过程[12].偏移方法可认为是一种试图将扭曲失真的影像恢复为正确影像的校正技术.偏移方法是基于惠更斯原理:波阵面上所有的点都可视作球面波的第二波源.如图1所示,波源S出发的波阵面信号在时刻t传播至接收器R并被记录下来.再利用记录的散(反)射波信号向波源S回传,声波速度为v,经过时间Δt沿声波传播方向回传vΔt距离至t−Δt时刻波阵面.根据时间反转法具有空间聚焦特性[13],回传波的波阵面与波源重合时,重构函数幅值达到最大,从而重构出缺陷的信息.

如图1所示,散射源位置记为A,非散射源位置记为B,接收传感器位置记为O.设A位置位移场经路径AO传播至O处的位移场为

图1 RTM缺陷成像原理Fig.1.Principle of RTM imaging for damage.

其中,ˆ表示为时域声位移场的傅里叶变换,ρAO表示AO的长度,GAO(ω)=AAO(ω)e−ikρAO为传递函数,AAO(ω)表示幅值,k为波数,此过程对应图1中的过程1.O位置处位移场时间反转后,经路径OA传播至A处的位移场为

其中∗表示复共轭,AO与OA路径相同,则ρAO=ρOA,GOA(ω)=GAO(ω),式中一项是实、偶、正函数,它在时间零点的傅里叶反变换是同相迭加的,会得到主相关峰值[14],这样回传出的波形幅值上得到增强,此过程对应图1中的过程2.O位置处位移场时间反转后,经路径OB传播至B处的位移场为

式中存在eik(ρAO−ρOB)相移分量,在时间零点傅里叶反变换并不能同相迭加,不能得到主相关峰值,幅值不会得到聚焦,此过程对应于图1中所示的过程3.实际缺陷监测过程中并不知道缺陷位置(A),但是O位置处位移场可以由接收传感器接收得到,时间反转处理后反向传播聚焦出缺陷位置.此外,A位置处的位移场为它是由激励信号传播至A位置后与缺陷相互散射产生,因此散射信号与入射场信号有很强的相关性,利用入射场信息可以明显提高缺陷重构效果,在3.3节中进行了数值验证.

O位置处位移场采集过程如图2所示,在板材上沿环线Xr装有阵列传感器,每个传感器既可以用作发射,也可以用作接收[15].在成像区域某位置处有一缺陷,如图2中阴影区域Σd所示.首先,在健康板上检测获取各个接收器的健康信号再在有缺陷的板上检测并记录各个接收器的总信号检测板材时,用一个激励传感器激发,同时所有接收传感器接收响应信号并记录.这样各传感器处的散射场为

其中,ˆ表示为时域声位移场的傅里叶变换.换一个激励传感器激励再重复上述步骤,从而俘获到各角度的缺陷信息.

图2 环形阵列结构示意图Fig.2.Schematic diagram of annular array structure.

RTM算法包含以下三个步骤[16]:1)单一激励源的声场正演传播;2)各个接收传感器接收到的散射波场时间反转后逆向回传外推;3)监测空间域互相关成像.第一步在激励传感器Xi处激发,在成像区域正演出各个点的位移场;第二步是将接收传感器Xj处频率域上的散射波场取共轭后逆向回传外推,得到成像区域各个点的位移场;第三步是在成像区域各点正演出的位移场与回传外推得到的位移场互相关处理,得出部分图像.再选取另外一个激励传感器激励并重复上述三个步骤,不同部分图像合成出最终图像.传播过程均运用格林函数进行传播,得到成像区域不同点处的位移场.假设由一对激励-接收传感器沿时间长度(0,T)记录的散射场经由逆向外推后的位移场为[16]

其中,φ表示对于给定点x的极角,如图2中所示.则由所有激励-接收传感器得到的合成图像为

后面的数值计算用(8)式进行缺陷重建.

3 数学建模

3.1 有限元模型建立

本文以商业有限元软件PZFlex构建有限元模型,如图3所示,数值仿真获取不同材料中缺陷的兰姆波散射信号,用RTM算法成像.

图3(a)中在厚度为2 mm的铝板(模型中d=1 mm,质量密度为2700 kg/m3,弹性模量70.753 GPa,泊松比0.33)上,在500 mm×500 mm的研究区域上向外延伸50 mm作为吸收边界,以此消除边界回波的影响,缺陷置于监测区域内.以板材几何中心为圆心,半径为200 mm处的圆上等间隔布置传感器,每个传感器既可以用作发射,也可以用作接收.传感器间隔为3.6°,3.6°方向传感器记为1号,依次记到360°(0°)方向传感器为100号.采用双元法激励[17],即在板上、下表面监测点上施加反对称载荷,实现单一S0模态Lamb波的激励.施加的激励信号选用中心频率为200 kHz的汉宁窗调制的5周期正弦波信号,在该频率下S0模式的波长λ=26.7 mm.图3(b)为碳纤维复合板材,铺层顺序为[0/45/90/−45]s,共8层,每层厚度0.25 mm,0°方向参数设定为:质量密度1200 kg/m3,c11=160.7,c12=6.44,c13=6.44,c22=13.92,c23=6.92,c33=13.92,c44=3.5,c55=7.07,c66=7.07,单位GPa.

图3 三维FE模型示意图 (a)铝板模型;(b)复合板材模型Fig.3.Schematic diagram of three-dimensional FE model:(a)Aluminum plate model;(b)composite plate model.

图4 铝板和复合板中S0模式的相速度曲线 (a)0°方向相速度频散曲线;(b)200 kHz时不同方向的相速度Fig.4.Phase velocity curves of S0mode in aluminum and composite plates:(a)Phase velocity dispersion curve in the 0°direction;(b)phase velocity in different directions at frequency 200 kHz.

图4给出了铝板和复合材料板中S0模式的相速度曲线.可以看到,S0模式在两种板材中的相速度频散曲线不同,如图4(a)所示.在相同激发频率下,S0模式在各向同性铝板与各向异性复合材料板中不同方向的相速度变化也不相同:在铝板中各个方向上的相速度相同,在复合材料板中各个方向的相速度不同,在30°和210°方向相速度较大,而150°和330°方向相速度较小,相速度的测量可参考文献[19].从图4(a)可以看出,激发频率200 kHz处铝板和复合板的相速度分别为5.3 km/s和7.38 km/s,与图4(b)极坐标中0°方向的相速度cp值符合.通过对两种板材中S0模式的相速度进行研究,得到Lamb波在不同传播方向上相速度的差异性,为后期在铝板和复合板上的缺陷成像奠定了基础.

3.2 模式分离预处理

当检测频率小于高阶模态的截止频率,以S0模态入射时,若缺陷为盲孔,将会在缺陷处产生模式转换,散射信号会包含S0,A0和SH0这三种模态信号的混叠.这三种模态信号在板材中的传播速度不同,若直接用于RTM成像将会有伪像影响,所以有必要进行模式分离预处理.可以利用其模态位移场的对称与反对称性,在上、下表面相对应的点设置两个信号采集点,将采集到的上、下表面信号投影到柱坐标系中,首先分离出面内位移中垂直于波传播方向的SH0模态信号,再对上、下表面位移作差和求和运算分离出S0和A0模态信号,实现兰姆波模态的分离[17].图5给出的是在第100号传感器激励,20,40,60,80,100号传感器接收的散射信号模式分离前后的时、频域信号.图5(a)是散射信号模式分离前的时域信号,其中存在S0,A0和SH0三种模态信号,由于单一S0模态激励,散射信号中S0模态信号占主要地位.图5(a)变换到频域后如图5(b)所示,A0和SH0等其他模态信号的干扰使波形产生振荡.但是经过模式分离处理后,分离出如图5(c)所示的S0单模态分量时域信号,将此信号变换到图5(d)所示的频域,消除了其他模式信号的干扰而产生的振荡,从而为后期的缺陷重构提供了保障.

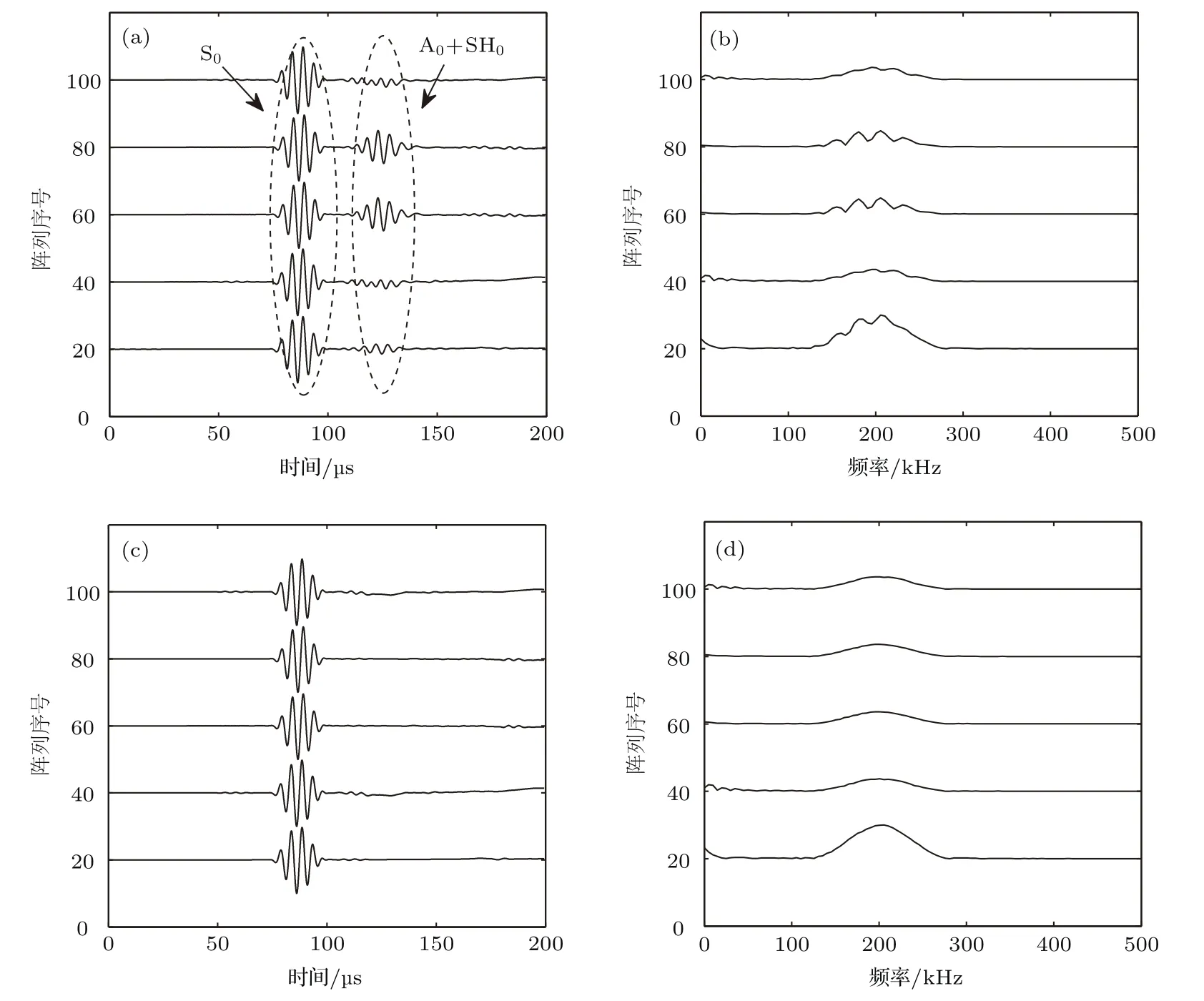
图5 模式分离前后的时、频域散射信号 (a)模式分离前的时域散射信号;(b)(a)的频域信号;(c)模式分离后的S0模态时域散射信号;(d)(c)的频域信号Fig.5.Scattering signals of time and frequency domains before and after mode separation:(a)Time domain scattering signal before mode separation;(b)frequency domain signals of(a);(c)S0mode time domain scattering signal after mode separation;(d)frequency domain signals of(c).

模式分离预处理对于RTM算法缺陷重构中伪像的消除具有显著作用,图6直观地对比了RTM算法有无模式分离预处理的缺陷重构效果.图6(a)为对于半径8 mm的位于铝板几何中心位置的圆形缺陷,直接用接收到的散射信号进行RTM缺陷重构的三维结果.图6(b)为图6(a)中的散射信号经模式分离后,用提取的S0模态散射信号进行RTM缺陷重构的三维结果.图6(c)给出了对于半径均为8 mm位于复合板中的邻近双圆形缺陷,直接用接收到的散射信号进行RTM缺陷重构的三维结果.图6(d)为图6(c)中的散射信号经模式分离后,用提取的S0模态散射信号RTM重构缺陷三维结果,坐标刻度为波长λ的整数倍.对于单缺陷,如图6(a)所示,重构缺陷结果已经出现了不可忽视的伪像;对于邻近双缺陷,如图6(c)所示,非S0模态散射信号经过RTM重构后会形成很多伪像,严重影响了缺陷的定位.从重建结果可以看到,经过模式分离预处理,将分离后的散射模态信号再进行RTM缺陷重构,可以有效减少干扰模态散射信号产生的伪像,为后期的复合板材中邻近缺陷,甚至不同深度的邻近缺陷的识别与重建提供了保障.

图6 有、无模式分离预处理的RTM算法缺陷三维重构结果 (a)无模式分离的铝板中心缺陷;(b)有模式分离的铝板中心缺陷;(c)无模式分离的复合板邻近双缺陷;(d)有模式分离的复合板邻近双缺陷Fig.6.Three-dimensional reconstruction results of damage by RTM algorithm with and without mode separation preprocessing:(a)Center damage in aluminum plate without mode separation;(b)center damage in aluminum plate with mode separation;(c)adjacent double damage in composite plate without mode separation;(d)adjacent double damage in composite plate with mode separation.

3.3 RTM成像机理数值分析

以半径8 mm位于铝板模型几何中心的圆形缺陷为例,图7揭示了频率域RTM成像的物理机理.图中给出的是第100号传感器激励,20,40,60,80,100号传感器接收信号的处理过程.图7(a)为第100号传感器激励,在非缺陷位置(−4λmm,0 mm)和缺陷位置(0 mm,0 mm)观测到的时域波形,图7(b)为对应图7(a)的频域波形,此过程为RTM中第一步;图7(c)为100号传感器激励,在20,40,60,80,100号传感器接收到的散射信号模式分离后,得到的S0单模态散射信号经时间反转后再在各自的传感器上加载,在非缺陷位置(−4λmm,0 mm)和缺陷位置(0 mm,0 mm)观测到频域波形,此过程为RTM中第二步;图7(d)为图7(b)与图7(c)中各信号相乘后得到的频域波形,此过程对应于RTM中第三步.其中,红色与蓝色曲线分别为非缺陷和缺陷处两个观测位置的信号波形.可以看到,图7(c)中,缺陷位置比非缺陷位置处的信号幅值大,这是传统时间反转成像的原理.经过互相关处理后,图7(d)中,缺陷位置比非缺陷位置的幅值明显增大,缺陷处得到了更好的聚焦.因此,综合利用入射场信息与散射场信息的RTM算法相比于仅用散射场信息的时间反转算法在缺陷重构上且有优越性.

图7 频率域RTM成像过程 (a)激励信号传播到观测点处的时域波形;(b)(a)的频率域波形;(c)散射信号时间反转后回传至观测点处的频域波形;(d)(b)与(c)中各信号互相关后的频域波形Fig.7.Frequency domain RTM imaging process:(a)The time domain waveform of an emitting signal propagating to an observation point;(b)frequency domain waveform of(a);(c)frequency domain waveforms of scattering signals backpropagating to the observation point;(d)frequency domain waveforms after(b)cross-correlation with each signal of(c).

3.4 不同缺陷RTM成像

为了进一步研究频域RTM算法对于不同位置多缺陷的识别潜力,这里给出了铝板和复合板内不同缺陷的重构结果.在图3模型上进行有限元数值模拟,针对不同位置的缺陷依次给出了铝板内非中心位置双缺陷以及复合板中相同深度、不同深度的邻近双缺陷重构结果.

图8所示为铝板内(−25 mm,−25 mm)和(−25 mm,25 mm)两个位置半径均为8 mm,深1.5 mm的双圆形缺陷重构结果.图8(a)为缺陷重构三维结果.图8(b)是截取图8(a)中y=1.0λ所得的剖面曲线,图8(c)是截取图8(a)中y=−1.0λ所得的剖面曲线,图8(d)是截取图8(a)中x=−0.9λ所得的剖面曲线,图中的虚线表示真实缺陷的尺寸与位置.从图8可以直观地判断出两缺陷位置分别为(−0.9λmm,−1.0λmm)(约 (−24.03 mm,−26.70 mm)) 和 (−0.9λmm,1.0λmm)(约(−24.03 mm,26.70 mm)). 从归一化的幅值大小对可以反应出两缺陷相同的深度情况.图8中各个剖面图,根据图示波峰宽度可以得出缺陷横向和纵向半径大小均近似为0.29λ(7.69 mm),接近于虚线所示实际半径8 mm的圆形缺陷,验证了频域RTM算法对于多缺陷的定位与信息重构的可实现性.

基于铝板的缺陷重建效果,本文拓展至复合材料探究频域RTM算法的重建效果.此时参考图4中复合板在200 kHz下,0°方向Lamb波传播相速度约为7.38 km/s,对应的波长λ约为36.8 mm,以此波长为成像坐标刻度.图9所示为复合板材上位于(−15 mm,−15 mm)和(−15 mm,15 mm),半径均为8 mm深1.5 mm的邻近双圆形缺陷重构结果.图9(a)为缺陷重构三维结果,图9(b)是截取图9(a)中y=0.51λ所得的剖面曲线,图9(c)是截取图9(a)中y=−0.51λ所得的剖面曲线,图9(d)是截取图9(a)中x=−0.51λ所得的剖面曲线,图中的虚线表示真实缺陷的尺寸与位置.从图9可以直观地判断出两缺陷位置分别为(−0.51λmm,−0.51λmm)(约为(−18.77 mm,−18.77 mm)),(−0.51λmm,0.51λmm)(约为(−18.77 mm,18.77 mm)).从归一化的幅值大小可以反应出两缺陷相同的深度情况.图9中各个剖面图,根据图示波峰宽度可以得出缺陷横向和纵向半径大小均近似为0.24λ(8.83 mm),接近于虚线所示实际半径8 mm.结果验证了频域RTM方法成功在复合板材上邻近双缺陷的定位与信息重构的可实现性.

图8 铝板内双圆形缺陷重构 (a)三维图像;(b)y=1.0λ剖面线;(c)y=−1.0λ剖面线;(d)x=−0.9λ剖面线Fig.8.Reconstruction of double circular damage in aluminum plate:(a)Three-dimensional result;(b)pro fi le view at y=1.0λ;(c)pro fi le view at y=−1.0λ;(d)pro fi le view at x=−0.9λ.

图9 复合板内邻近双圆形缺陷重构 (a)三维图像;(b)y=0.51λ剖面线;(c)y=−0.51λ剖面线;(d)x=−0.51λ剖面线Fig.9.Reconstruction of double circular adjacent damage in composite plate:(a)Three-dimensional result;(b)pro fi le view at y=0.51λ;(c)pro fi le view at y=−0.51λ;(d)pro fi le view at x=−0.51λ.

图10 复合板材不同深度双圆形缺陷重构 (a)三维图像;(b)y=0.51λ剖面线;(c)y=−0.51λ剖面线;(d)x=−0.51λ剖面线Fig.10.Reconstruction of double circular damage in composite plate with different depths:(a)Three-dimensional result;(b)pro fi le view at y=0.51λ;(c)pro fi le view at y=−0.51λ;(d)pro fi le view at x=−0.51λ.

图10所示为复合板材上位于(−15 mm,−15 mm)和(−15 mm,15 mm),半径均为8 mm、深度分别为h1=1.5 mm,h2=1 mm(h2=0.67h1)的邻近双圆形缺陷重构结果.图10(a)为缺陷重构三维结果,图10(b)是截取图10(a)中y=0.51λ所得的剖面曲线,图10(c)是截取图10(a)中y=−0.51λ所得的剖面曲线,图10(d)是截取图10(a)中x=−0.51λ所得的剖面曲线,图中的虚线表示真实缺陷的尺寸与位置. 从重构结果的x/y剖面图可以看出,缺陷位置分别为(−0.49λmm,−0.50λmm)(约(−18.32mm,−18.40mm))和(−0.51λmm,0.50λmm)(约(−18.77 mm,18.40 mm)),深度为1.5 mm的缺陷半径大小近似为0.24λ(8.83 mm)接近于虚线所示实际半径8 mm,而深度为1 mm的缺陷纵向半径约为0.16λ(5.89 mm)相比于真实缺陷半径偏小.同时,对比x剖面的图10(b)和图10(c)的波峰幅值与y剖面的图10(d)中双缺陷波峰幅值,可以得到重构出的缺陷深度h2约为0.7h1,符合实际缺陷的深度信息h2=0.67h1.如图10(a)和图10(d)所示,当两个缺陷深度不同时,不仅会影响缺陷的重建精度,而且会在两缺陷之间会产生伪像,这是因为S0模态传播至不同深度缺陷时,在两缺陷处发生不同程度的散射,这两部分散射信号相互作用,又会在两缺陷边界重新产生二次甚至多次散射信号.

4 结 论

本文建立了超声兰姆波与缺陷相互作用的有限元仿真模型,并利用环形阵列传感器激发声场和接收缺陷散射信号.在声场分析方面:应用格林函数分析了兰姆波的正向传播过程,以及缺陷散射波的反向传播过程,并在频域分析对比损伤处与非损伤处的波形,观察到利用入射场信息的RTM算法较传统时间反转算法增强了损伤位置波场的幅值.在缺陷重构方面:分别对比有无模式分离的频域RTM算法对铝板内中心圆形缺陷以及复合板材内邻近双缺陷的重构效果;采用频域RTM方法对铝板内不同位置的双缺陷进行重构,拓展频域RTM方法对复合板材内位置相近、深度相同以及深度不同的双缺陷重构.数值结果表明,模式分离预处理能有效消除干扰模态散射信号造成的伪像.而且环形阵列布置方式由于能充分利用缺陷的全角度散射信号,因而更加精确地重现了缺陷形貌.

[1]Monkhouse R S C,Wilcox P D,Cawley P 1997Ultrasonics35 489

[2]Lin X,Yuan F G 2001AIAA J.39 2206

[3]Whitmore N D 19831983 SEG Annual MeetingLas Vegas,Nevada,USA,September 11–15,1983 p382

[4]Arnal B,Pernot M,Tanter M 20102010 IEEE Ultrasonics Symposium(IUS)San Diego,USA,October 11–14,2010 p1039

[5]Anderson B E,Gri ff a M,Bas P Y L,Ulrich T J,Johonson P A 2011J.Acoust.Soc.Am.129 EL8

[6]Fink M 1992IEEE Trans.Ultrason.Ferr.39 555

[7]Müller S,Niederleithinger E,Bohlen T 2012Int.J.Geophys.2012 128465

[8]Ma F Z,Guo S J,Wang J 2016Prog.Geophys.31 741(in Chinese)[马方正,郭书娟,王杰 2016地球物理学进展31 741]

[9]Lin X,Yuan F G 2005Struct.Health.Monit.4 341

[10]Zheng L,Guo J Z 2016Acta Phys.Sin.65 044305(in Chinese)[郑莉,郭建中 2016物理学报 65 044305]

[11]Xu Y F,Hu W X 2014Acta Phys.Sin.63 154302(in Chinese)[徐琰锋,胡文祥 2014物理学报 63 154302]

[12]Claerbout J F 1971Geophysics36 467

[13]Qiu L,Yuan S F,Zhang X Y,Wang Q,Zhang B L,Yang W W 2010Acta Mater.Compos.Sin.27 101(in Chinese)[邱雷,袁慎芳,张逍越,王强,张炳良,杨伟伟2010复合材料学报27 101]

[14]Wang Q,Yuan S F,Qiu L,Sun Y J 2008Chin.J.Sci.Instrum.29 1816(in Chinese)[王强,袁慎芳,邱雷,孙亚杰2008仪器仪表学报29 1816]

[15]Rose L R F,Wang C H,Chan E 2015Wave Motion58 222

[16]Xu K,Zhou B,McMechan G A 2010Geophysics75 61

[17]Zheng Y,Zhou J J 2014Eng.Plast.Appl.31 21(in Chinese)[郑阳,周进节 2014工程力学 31 21]

[18]Chan E,Rose L R F,Wang C H 2015Ultrasonics59 1

[19]Wang L,Yuan F G 2005Struct.Health.Monit.4 3

PACS:43.20.+g,43.35.+d DOI:10.7498/aps.66.214301

*Project supported by the National Natural Science Foundation of China(Grant Nos.11674214,11474195,51478258)and the Key Technology R&D Project of Shanghai Committee of Science and Technology,China(Grant No.16030501400).

†Corresponding author.E-mail:hyzh@shu.edu.cn

Reverse time migration Lamb wave imaging based on mode separation∗

Zhang Hai-Yan1)†Yang Jie1)Fan Guo-Peng1)Zhu Wen-Fa1)2)Chai Xiao-Dong2)

1)(School of Communication and Information Engineering,Shanghai University,Shanghai 200444,China)
2)(School of Urban Railway Transportation,Shanghai University of Engineering Science,Shanghai 201620,China)

d 31 May 2017;revised manuscript

30 June 2017)

Frequency domain reverse time migration method is used to reconstruct damages in isotropic and anisotropic plates.Considering multimode overlapping,the Lamb wave signals scattered by the defects may result in artifacts in defect imaging.The scattering signals are thus pre-processed by using a mode separation method based on the vibration symmetry di ff erence between the fundamental guided modes.Based on the multi-element array ultrasonic technique,a numerical study is carried out for defect imaging of aluminum and composite plates by using the frequency reverse time migration method.This paper is organized as follows.Firstly,in order to capture multi-directional information about damages,scattering Lamb wave signals caused by the defects are numerically collected by an annular array of transducers through using the finite element simulation.Secondly,after the pre-processing of mode separation,the separated scattering signals are time-reversed and used to stimulate the corresponding receivers.The Green’s function is utilized to back-propagate the scattering Lamb signals in frequency domain,so that the back-propagated acoustic field information of monitored area can be obtained.Finally,the defect images are reconstructed by the cross-correlation between the incident acoustic field and the back-propagated acoustic field.To illustrate the in fluence of mode separation,the numerical experiments are carried out on an aluminum plate with single defect and on another composite plate with two adjacent identical defects.The reconstructed results from frequency domain reverse time migration method with and without mode separation are compared.The comparison indicates the importance of mode separation.Furthermore,the method is extended to detecting the double adjacent defects with different depths in the composite plate.The imaging result illustrates that the presupposed two adjacent defects with different depths are successfully identified.Numerical results demonstrate that the pre-processing of mode separation helps to effectively remove the artifacts resulting from the multimode interference in the imaging process.The proposed frequency reverse time migration method presents a strong potential for detecting and imaging defects in isotropic and anisotropic plates,which is capable of accurately measuring multi-site defects with information about geometry,size and depth.

Lamb wave,reverse time migration,ring sensor array,mode separation

应用频率域逆时偏移方法实现各向同性和各向异性板中缺陷的兰姆波成像.由于缺陷引起的多模态散射信号会在重建图像中形成伪像,根据基本导波模式振动对称性的差别进行了模式分离预处理.基于多元阵列超声技术,开展了铝板和复合板内缺陷频率域逆时偏移超声成像方法的数值仿真研究.首先,建立有限元模型,采用环形传感器数值采集由缺陷引起的兰姆波散射信号,然后,将采集到的多模式散射信号进行模式分离处理,再将模式分离后的兰姆波散射信号经时间反转后并在相应的接收器处重新激励,在频域中运用格林函数反向传播兰姆波散射信号,获取监测区域的声场信息,与正向传播声场进行互相关,重建缺陷图像.首先对铝板中单缺陷以及复合材料板中相邻的两个相同缺陷进行数值仿真,对比有无模式分离处理的缺陷逆时偏移成像效果,体现出模式分离的重要性.在此基础上,采用逆时偏移方法对复合板材内位置邻近、深度不同的双缺陷进行识别.数值结果表明,模式分离预处理后的缺陷重建图像能够有效去除多模式干扰产生的伪像.文中提出的成像方法对各向同性板和各向异性板内缺陷的检测和成像具有很好的发展潜力,可以准确地探测多个缺陷的形状、尺寸和深度.

10.7498/aps.66.214301

∗国家自然科学基金(批准号:11674214,11474195,51478258)和上海市科委重点支撑项目(批准号:16030501400)资助的课题.

†通信作者.E-mail:hyzh@shu.edu.cn

©2017中国物理学会Chinese Physical Society