实现粒子布居高效转移的两种激光脉冲时序方案的理论研究∗
2017-11-10张露严璐瑶鲍洄含柴晓茜马丹丹吴倩楠夏凌晨姚丹钱静
张露 严璐瑶 鲍洄含 柴晓茜 马丹丹 吴倩楠 夏凌晨 姚丹 钱静
(华东师范大学物理与材料科学学院,光与原子量子所,上海 200062)
实现粒子布居高效转移的两种激光脉冲时序方案的理论研究∗
张露 严璐瑶 鲍洄含 柴晓茜 马丹丹 吴倩楠 夏凌晨 姚丹 钱静†
(华东师范大学物理与材料科学学院,光与原子量子所,上海 200062)
(2017年5月23日收到;2017年7月11日收到修改稿)
受激拉曼绝热通道,布居转移,绝热条件,纠缠态
1 引 言
相干布居转移的目的是在各分离量子态之间通过适当的耦合场有效地转移粒子布居数,通常由受激拉曼绝热通道(stimulated Raman adiabatic passage,STIRAP)实现.STIRAP的成功一方面在于抑制了转移过程中中间能级的作用,甚至在转移时间远大于中间能级寿命的情况下也有望获得极高的效率;另一方面它极大地消除了实验条件如光场幅值、脉冲时序、激光波形等的微小变化带来的影响.因此,STIRAP技术凭借其得天独厚的优势,自Gaubatz等[1]提出以来已在原子分子光物理(AMO)、化学、工程技术学的一些领域广泛应用.
STIRAP技术的物理本质是通过施加一对逆序列的(光)脉冲耦合相应的量子态,抽运光作用于初始态和中间态,斯托克斯光作用于中间态和末态,且斯托克斯光超前抽运光(逆序列),从而构造一个只包含初末量子态的绝热本征态(也称暗态).当体系始终跟随暗态发生演化时,能够消除中间激发态自发辐射的影响,使初末态之间粒子布居数完全转移.基于简单的Λ或梯型三能级结构实现STIRAP的基本理论已经有了完备的阐述[1],随着研究深入,逐渐在复杂的多能级系统里设计出多种STIRAP结构来满足不同性质粒子转移的需求.现有的特殊结构有:Straddle-STIRAP[2,3],Tripod-STIRAP[4,5],Chainwise-STIRAP[6,7]等.除了这些复杂结构之外,STIRAP的成功实现对AMO领域的发展有特别重要的意义.它可以用于实现目标原子态的相干囚禁和电子激发[8−10]、超冷基态分子的制备[11,12]、离子的相干囚禁和测量[13,14]、原子光学器件(原子镜、原子分束器、原子干涉仪)的研发[15,16]以及腔量子电动力学系统的操控[17,18].尤为值得一提的是,利用STIRAP技术在实验上将磁Feshbach共振(FR)下产生的弱束缚分子高效相干地转移到分子基态上,成功制备了异核极性超冷基态分子KRb[19,20](由美国JILA实验室的Jun Ye和D.S.Jin小组于2008年完成),毋庸置疑地推动了之后冷分子物理的飞速发展.迄今为止,实验上成功制备的超冷分子包括同核分子Rb2[21],Sr2[22],Cs2[11],Na2[23]和异核分子KRb[19,24],RbCs[25,26],NaK[27],RbSr[12],NaRb[28]等.Amsterdam大学的Schtrck小组[29]最新的实验工作将光缔合(photoassociation,PA)后的Sr原子对经由STIRAP相干转移到分子基态,效率达80%以上,比2012年文献[22]报道的结果提高了2.5倍.针对某些磁FR不适合的原子种类或能级来说,使用PA技术(光学方法)产生弱束缚分子无外乎是另一条途径.
目前,制备超冷基态分子常用的方法是PA+STIRAP和FR+STIRAP,取决于分子的能级结构和自身属性.与原子相比,分子能级更加复杂,实验上倾向于采用多能级级联的构型来转移PA或FR产生的弱束缚分子,既增强能级间的耦合强度又减小所需的光功率.2010年,Innsbruck大学的Danzl等[11]利用五能级M型能级结构将磁FR产生的Cs2从高振动态|v=155〉逐步转移到振转基态|v=0,J=0〉.为此目的,实验中他们采用了两种不同的STIRAP方案,即所施加四束激光的时序和种类(连续性、脉冲型)不同,分别为四光子型STIRAP(4p-STIRAP,简称4p)和连续型STIRAP(s-STIRAP,简称s),获得的转移效率均在0.60左右.文献[11]中虽然对光晶格深度、分子能级寿命、能级失谐量等重要参量做了讨论,但未能详细地解释效率较低的原因,对两种方案物理本质的异同点也未做比较和论述.
本文系统地研究了两种方案实现粒子布居数相干有效转移的基本原理,详细探讨了转移效率与能级性质和光场参数的依赖关系.通过比较激发态和亚稳态能级的自发辐射率、激发态能级的失谐、脉冲激光之间的时间间隔和幅值等物理参量对转移效率的影响,在符合绝热条件的基础上提出优化各参量实现最佳粒子布居转移的可能性.分析可知,与理论预测的最佳效率0.97相比,激发态能级的自发辐射率过大是限制实验获得高转移效率的关键因素.值得注意的是,虽然本方案始于Cs2实验,但在文中我们对该模型作更加普适的研究,故以“粒子”替代“分子”的说法.最后,对方案可行性的分析和在纠缠态制备方面的论述进一步加深了本文的研究意义.
2 模 型
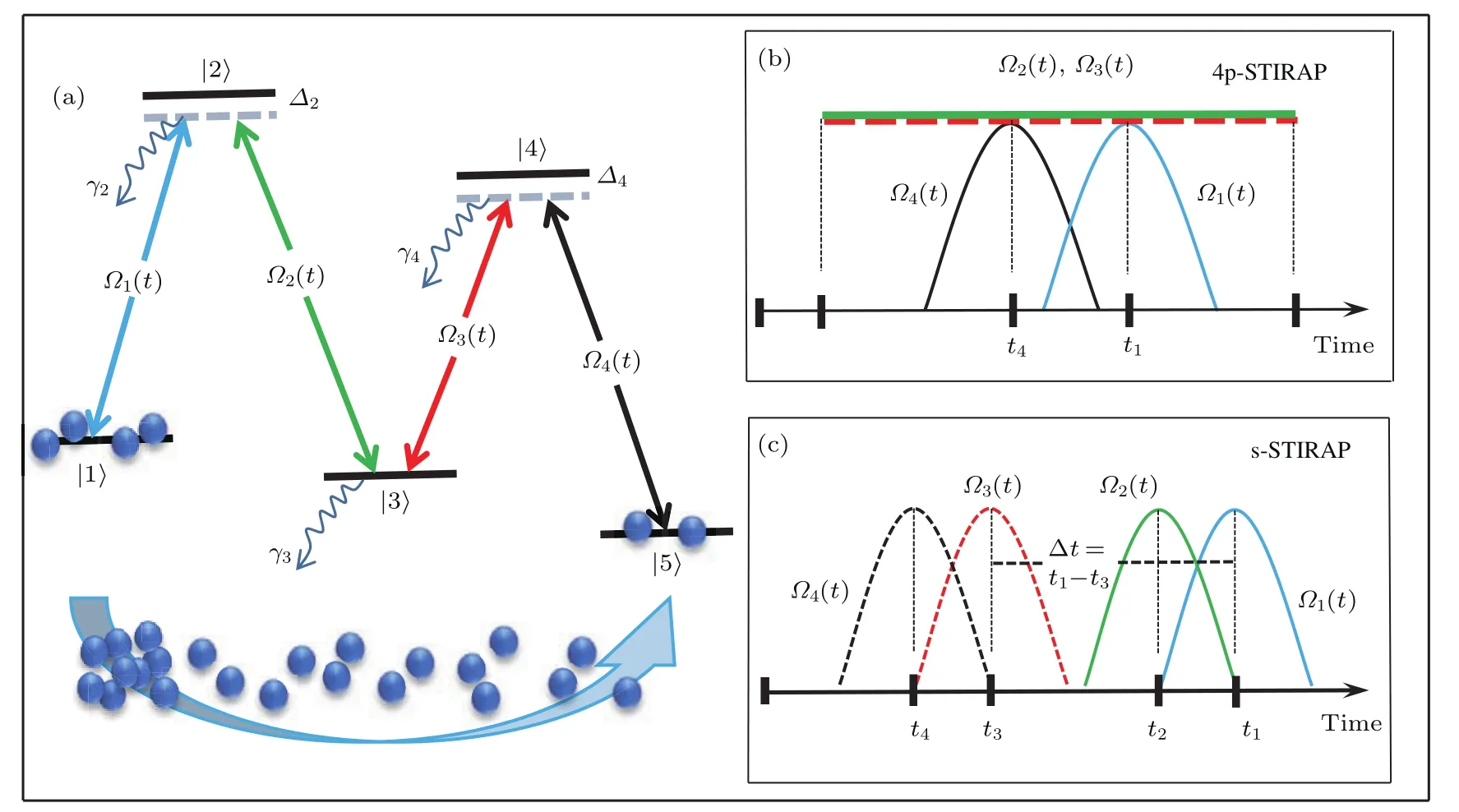
图1 (网刊彩色)(a)M型五能级系统的示意图;(b)4p-STIRAP型激光脉冲时序图;(c)s-STIRAP型激光光脉冲时序图;具体的参数详见正文Fig.1.(color online)(a)Schematic representation of a M-type fi ve-level system;time-dependence of the adopted laser Rabi frequencies Ωi(t)(i=1,···,4)are described in(b)4p-STIRAP-type scheme and(c)s-STIRAP-type scheme.See main texts for relevant parameter descriptions.
考虑一个五能级级联系统,如图1(a)所示,包含粒子能级|i〉(i=1,2,···,5),其中|1〉,|5〉,|3〉分别对应初末态和亚稳态,|2〉和|4〉对应激发态.利用外加激光场Ωi(t)(i=1,···,4)耦合能级|i〉和|i+1〉,Δi表示能级|i〉的失谐量.假定初始态|1〉和目标态|5〉都是绝对稳定的,而中间态|2〉,|3〉,|4〉能级寿命有限,用自发辐射率γi(i=2,3,4)表示.研究目的是将初始制备在态|1〉上的粒子经过一系列中间能级转移到更加稳定的末态|5〉上.在整个过程中,不仅要求极大地抑制中间能级|2〉,|3〉,|4〉上的布居数,而且尽可能实现最大的转移效率η(η~P5,t→∞/P1,t→0,Pi,t表示t时刻|i〉上的布居).为此目的,我们采用两种不同的STIRAP方案,通过优化激光场脉冲的时序建立初末两态之间的直接关联,实现粒子布居的高效转移[30].值得注意的是,能级寿命与其自发辐射率成反比例,这类多能级STIRAP若转移过程时间与能级寿命相当可导致大量粒子由激发态能级的自发辐射损失.另外,多能级级联的光耦合方式相较于三能级Λ方案实验操作相对复杂,包含超精细能级,但有望解决自由-束缚能级之间偶极跃迁矩阵元(Franck-Condon系数)太小的缺点,在超冷分子产生方面有十分广泛的应用[31,32].
基于以上的分析,系统的哈密顿量可以写成(ħ=1)
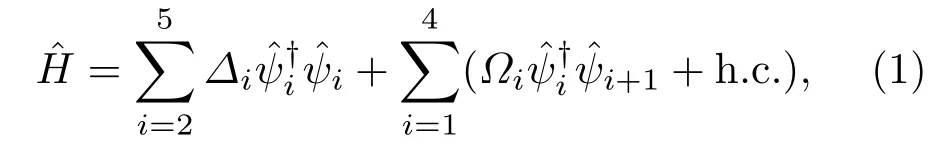
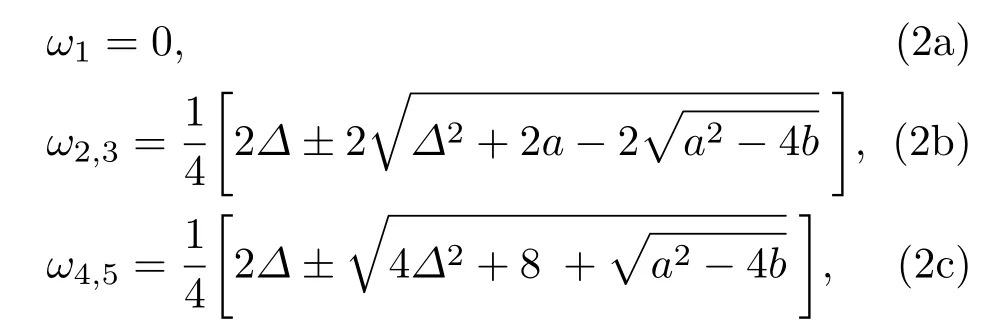
(2b)和(2c)式中,a=在推导过程中,运用了双(四)光子共振条件:Δ3=Δ5=0,并设定单(三)光子失谐量为Δ2=Δ4=Δ.显然,本征能量ω1=0对应的本征态|ω1〉即STIRAP过程依赖的“准暗态”, 而|ωj〉(j=2,···,5)称为亮态[33,34].这里,定义“准暗态”的原因是区别传统三能级Λ或梯型系统中构建的直接联系初末两态,完全不受中间态影响的相干布居囚禁态(即暗态)[6].各能量本征态的具体表达式如下(为简化解析表示,暂令Δ=0):
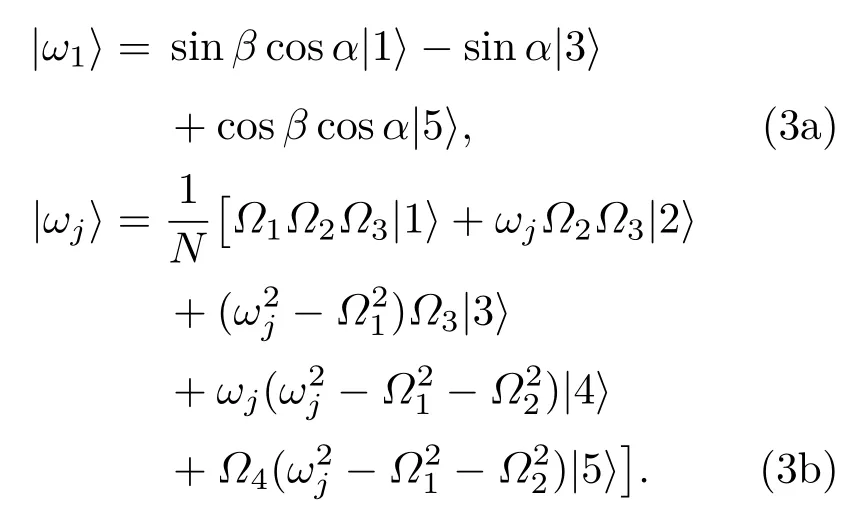
(3b)式中,N是归一化常数;(3a)式中,α和β为包含光场拉比频率的混合角,具体形式是
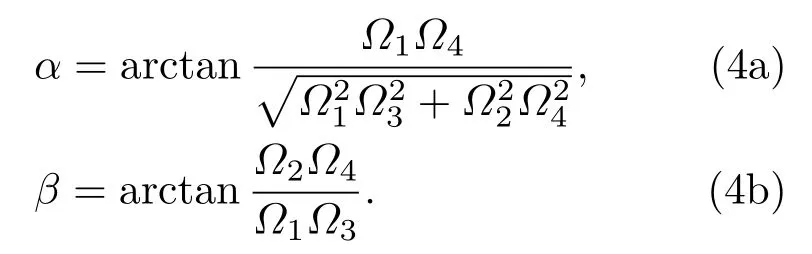
与亮态|ωj〉不同, 准暗态|ω1〉只包含裸态|1〉,|3〉,|5〉,故不受中间激发态|2〉,|4〉的影响,但亚稳态|3〉在绝热演化中起着至关重要的作用.因为布居在态|3〉上粒子数概率~|sinα|2持续以γ3的速率损失,这也是|ω1〉被称之为“准暗态”的原因.为了抑制这种损耗必须保持sinα≈0(α≈0),根据α的定义需要满足条件:Ω3≫Ω4或Ω2≫Ω1.在此基础上,|ω1〉可化简为
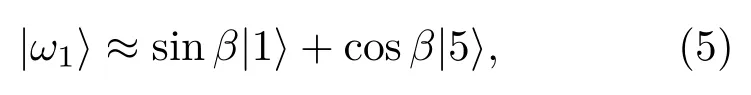
结合β的定义式(4b)与(5)式可知,若适当优化并操控激光脉冲的时序便可以实现粒子布居数在态|1〉和|5〉之间的高效转移,同时若β可于[0,π/2]之间任意调控,将有望实现可控量子纠缠态的制备.
由上述分析并结合实验结果[11],采用两种激光脉冲时序方案:1)4p方案和2)s方案,脉冲时序分别如图1(b)和图1(c).在4p方案中,Ω1(t)和Ω4(t)构成一对逆序的STIRAP光脉冲(Ω4(t)部分超前于Ω1(t)),Ω2(t)和Ω3(t)是两束等幅连续光且它们的幅值远大于Ω1(t)和Ω4(t).这样的设计能够有效确保粒子布居沿着单一的绝热本征态|ω1〉转移,而辅助的较强的中间连续光也抑制了亚稳态能级|3〉的布居.在s方案中,施加两对连续的STIRAP脉冲分两步完成|1〉→|5〉的跃迁,它们分别是:Ω1(t)和Ω2(t)完成|1〉→|3〉的跃迁,Ω3(t)和Ω4(t)完成|3〉→|5〉的跃迁.两对脉冲对之间相对时间间隔定义为Δt=t1−t3,通过改变并优化Δt实现对亚稳态上布居数的抑制,从而提高转移效率.因此,s方案的关键在于控制光脉冲对之间的相对时差,而4p方案只需严格控制脉冲光的开关时间即可,实验操作上相对容易.
在数值计算中,采用高斯型脉冲光场,光场拉比频率可表示为
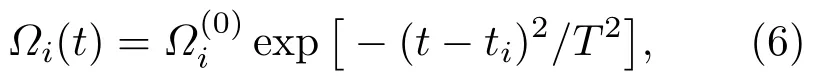
3 数值模型
3.1 绝热参数
4p(s)方案光脉冲时序的设计本质上都是基于准暗态|ω1〉的存在.理想情况下,若系统的真实动力学演化能够完美地跟随|ω1〉,粒子布居数从|1〉→|5〉的转移应是绝对的.考虑真实情况,由于外界扰动、体系退相干等诸多因素的影响,即便再微小的扰动也有可能破坏绝热性,导致体系的演化无法绝对地跟随|ω1〉,存在一定概率被激发到临近本征态上,如|ω2〉,|ω3〉. 而亮态|ωj〉受到激发态能级寿命的牵制,极大地影响了转移效率.注意到实验[11]中基态Cs2的产生效率均只有0.6左右.为了定量衡量体系绝热演化偏离准暗态的程度,引入绝热参数r(t)表示亮态|ωj〉上的总布居数[35].
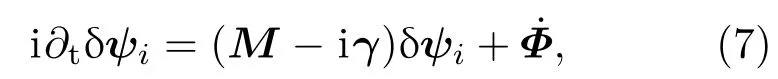
式中,
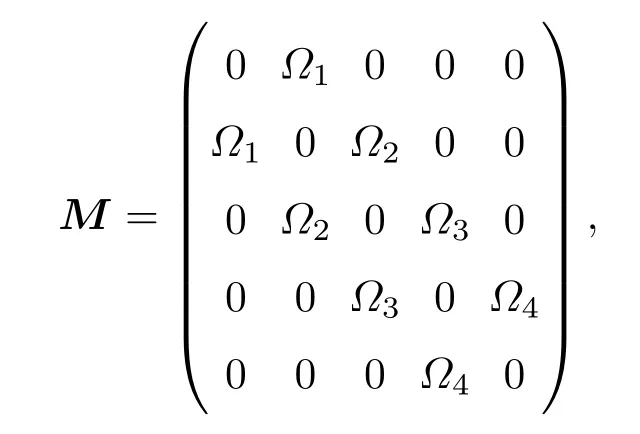
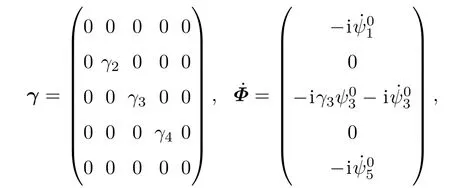
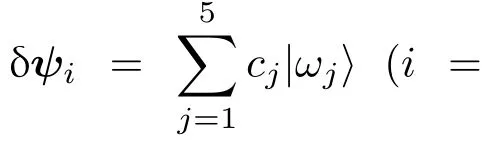
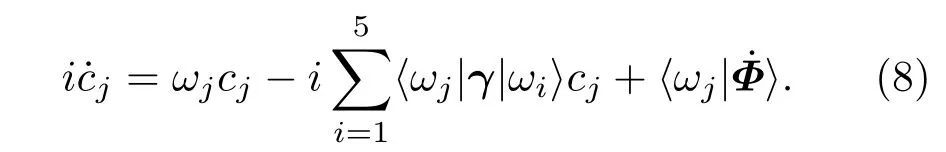
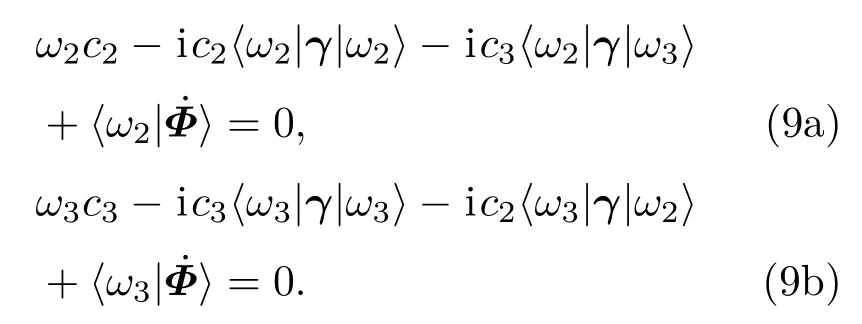
因此,绝热参数r(t)可定义为[35]
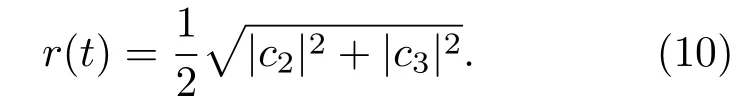
直接求解(9a)和(9b)式,并将结果代入(10)式可导出绝热参数r(t)的解析表达式.由于该形式较复杂,需要在数值上进行研究.r(t)≪1表示系统的绝热性非常好,大多数粒子都可以保持在准暗态|ω1〉演化而不被激发到临近的亮态上.
3.2 转移效率

系统的粒子布居转移效率可定义为Pi,t≡|ψi(t)|2表示t时刻|i〉上的布居数.考虑总粒子数概率归一且守恒,η实则表示末时刻|5〉上的布居.取γ2=γ4≡Γ,令Γ(Γ−1)作为系统无量纲的频率(时间)单位.相关参量的定义如下:=1.6×2π.其余参数分别为(上标4p或s对应方案名):
1)4p方案中,
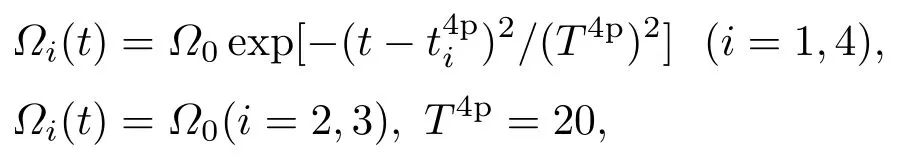
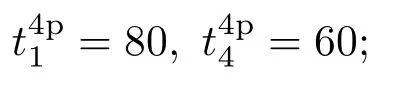
2)s方案中,
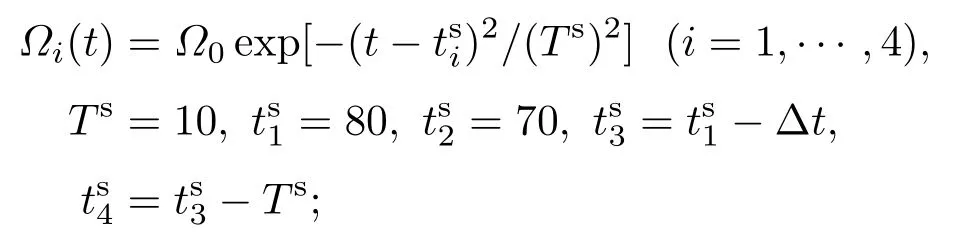
改变Δt可移动光脉冲Ω3(t)和Ω4(t)的中心位置,而它们的部分重合区始终不变;同理,Ω1(t)和Ω2(t)的相对位置也固定.
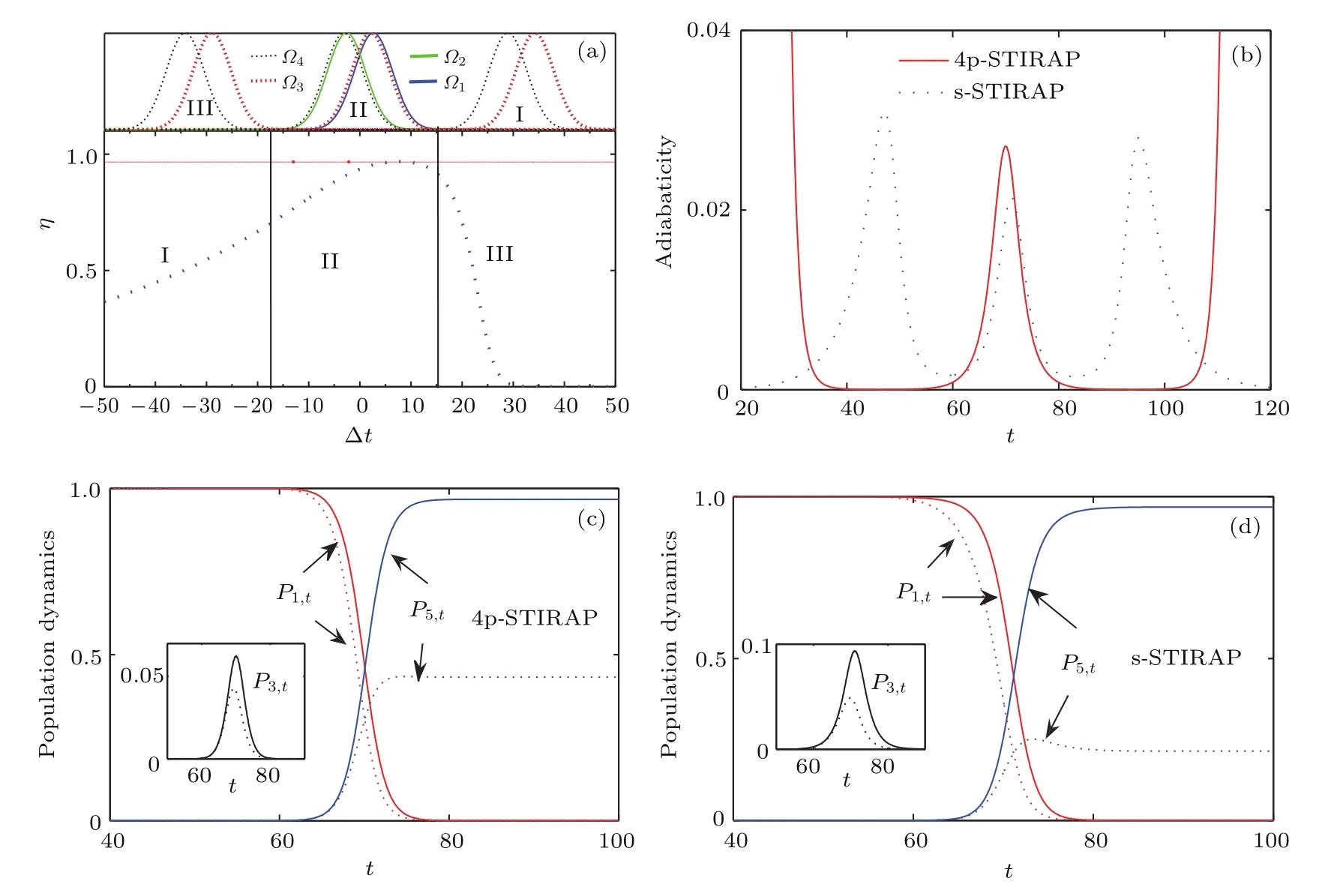
图2 (网刊彩色)(a)转移效率η与脉冲时间间隔Δt的依赖关系,内插图表示在区域I,II,III中激光脉冲的时间顺序,其中Ω1和Ω2位置固定;(b)4p和s方案下绝热参数r(t)的比较,取s方案下Δt=7.8(最佳值,区域II中);(c),(d)各能级布居数P1,t(红色实线和虚线),P3,t(插图,黑色实线和虚线),P5,t(蓝色实线和虚线)随时间的演化;为便于比较,实线和虚线分别表示γ=0.01和γ=1两种情况Fig.2.(color online)(a)Transfer efficiency η as a function of the pulse delay Δt=t1−t3for 4p(red solid)and s(blue dashed)schemes.The inset shows the time order of the laser pulses in regions I,II,III,where Ω1and Ω2are fi xed.(b)Adiabaticity versus time for 4p(red solid)and s(blue dashed)schemes.In s-STIRAP scheme,we choose Δt=7.8(optimal).(c)In 4p scheme,time-dependent population dynamics of initial state P1,t(red lines),metastable state P3,t(black lines)and fi nal state P5,t(blue lines).Two cases of γ =0.01(solid lines)and γ =1(dashed lines)are compared.Same results are shown in(d)except for the s scheme.All frequencies are scaled by Γ.
基于以上的参数设定,对两种方案下的系统动力学演化进行定量研究.首先重点关注光脉冲对的相对时差Δt在s方案中的作用.为了方便比较,同时呈现了相同参数下4p方案下的结果.图2(a)描绘了η-Δt关系曲线,红色实线(蓝色虚线)表示4p(s)方案的结果.根据定义,4p方案的η与Δt无关,只要优化其余激光参数值就能获得极高的效率,在这组参数下,效率可高达η≈0.97.但s方案中,区域II内的最大效率可达η≈0.97(Δt≈7.8),增加或者减小Δt都使η明显降低.尤其是在区域III(Δt>15)中,η迅速降为0.分析其原因,在区域II中,光脉冲的时序满足Ω4-Ω2-Ω3-Ω1这样的逆序列关系(Ω4超前Ω3,Ω2超前Ω1),且它们之间的重叠面积非常大.但是在区域I和III中,脉冲序列Ω1和Ω2,Ω3和Ω4虽各自都满足逆序关系,两对脉冲对之间重叠面积却大大缩小.尤其是区域III,先施加的Ω3和Ω4在亚稳态|3〉和末态|5〉之间构建起关联,但是当Ω1和Ω2到来时,Ω3和Ω4已经降为零,几乎没有作用.所以,绝大多数粒子最终停留在态|3〉而不会被转移到目标态|5〉,导致转移效率η大大降低.为了说明体系的演化保持着很好的绝热性,图2(b)比较了两种方案下绝热参数r(t)的大小,发现不论4p(红色实线)或是s(蓝色虚线)方案,在光-粒子相互作用区(60<t<80)都表现出非常好的绝热性,满足r(t)≈0.02≪1,与图2(a)的结果非常符合.这说明在优化的光场参数下,它们都沿着准暗态做绝热演化,实现高保真度的粒子布居数转移.
结合图2(a)和图2(b)的计算结果,两种方案下系统真实的布居数随时间演化规律可参见图2(c)和图2(d).初始态、中间亚稳态、末态上的布居数P1,t,P3,t(见插图)和P5,t分别用红线、黑线、蓝线表示,实线和虚线对应γ=0.01和γ=1.0两种情形.由准暗态表达式(3a)可知,态|3〉的自发辐射率γ必定影响η,所以在图2(c)和图2(d)中考虑了不同γ值下的动力学演化,通过比较P5,t→∞对γ变化的敏感程度可以定性上判定态|3〉布居的大小.由图2(c)和图2(d)可知,当γ=0.01时,两种方案下η都非常高.然而,γ增加到1.0时,s方案较4p方案P5,t→∞的降幅更大,从而可以反推s方案下态|3〉上的布居数更大.这与图2(c)和图2(d)内插图给出的P3,t的结果完全一致,因为此外,中间激发态的布居数P2,t和P4,t始终非常小,约10−3,故在图上没有给出.
综上所述,可以得到以下初步结论:
1)在适当参数的选取下,两种方案均能实现高效的粒子布居转移,理论上预估的最佳值均达η~0.97;
2)转移效率随中间亚稳态自发辐射率γ的增大明显减小,但相同条件下,s方案对γ的依赖程度更大一些;
3)绝热参数r(t)能够作为表征转移效率高低的定性判据,在光-粒子相互作用区,r(t)≪1表示系统的动力学跟随准暗态本征态演化,可实现较高的转移效率.
4 结果与讨论
在4p(s)方案中,考虑其他相关参量,包括能级的失谐量、激发态的自发辐射率、激光脉冲的幅值等都会对两种方案的运作造成不同的影响,下面逐一分析.
4.1 激发态能级失谐量
由(2a)—(2c)式可知,能量本征值均与Δ有关.Δ=0时,ω2,3的分布与ω1(=0)之间上下对称且相距较远,粒子不易被激发到|ω2〉或|ω3〉上. 随着|Δ|的增加,ω2,3随之发生能级平移,致使ω2或ω3更加接近ω1(=0),因此布居转移偏离|ω1〉的可能性变大,绝热条件被破坏,转移效率也将随之降低.
图3(a)描绘了η-Δ的关系曲线,与上述定性分析一致,随着|Δ|的增加,η确实明显减小,且4p方案(红色实线)与s方案(蓝色虚线)相比,η的降速更快.这与实验结果(文献[11]中图3(a)和图3(c))及理论分析都完全符合,即最佳的转移效率出现在共振Δ=0处.此外,始终满足η4p<ηs,尤其是在|Δ|>50大失谐区域,η4p随|Δ|增加而下降的速率远大于ηs.要理解这一点,可以比较两种方案在Δ=0和Δ=50两处的绝热参数曲线,如图3(b1)和图3(b2)所示.
当Δ=0时,在光-粒子相互作用区(60<t<80),绝热参数r(t)的最大值均小于0.03(满足r(t)≪1的条件),故粒子布居的转移效率很高,η~0.97.但当Δ增加到50时,r(t)提高了一个数量级.尤其在作用区,我们发现r4p>rs,表明4p方案下绝热性被破坏的程度更高(有部分粒子被激发到亮态本征态),相应的η4p也更小.这与图3(a)所示的η4p<ηs的结果十分符合.
4.2 能级自发辐射率
在数值模型中已经对4p(s)方案下η对中间亚稳态自发辐射率γ的不同依赖程度做了初步的解释,下面进一步讨论激发态和亚稳态能级自发辐射率γ和Γ对STIRAP过程的不同作用.理想情况,若准暗态|ω1〉被绝对地跟随,根据定义转移效率仅仅与γ有关.真实的动力学演化不可避免地会有部分粒子被激发,相应地这些激发能级的自发辐射率Γ也会影响转移效率.直觉上,η与γ和Γ应成反关联,即增加γ和Γ都导致η的减小.这一结论也可以从绝热参数的解析解中得到对应.
图4(a)和图4(b)分别呈现η-γ和η-Γ的依赖关系.总体而言,伴随γ或Γ的增加,η均急剧减小至0,与理论预估的结论非常符合.因为能级自发辐射率的增加必然破坏体系绝热性,导致大量粒子的损失从而降低了η.比较图4(a)和图4(b)还可以发现更多有趣的结果.
1)γ较Γ能更快促使η→0.原因是准暗态|ω1〉只显含态|3〉,并不包含|2〉和|4〉,所以理想情况η不依赖Γ的变化,而必须依赖γ.η对Γ变化敏感主要来自于系统真实演化无法绝对跟随准暗态的变化所致.通常,布居数P2,t和P4,t始终非常小,约10−3,而P3,t与之相比可达0.1.
2)ηs(γ)<η4p(γ). 中间亚稳态|3〉在s方案中起到了连接两个Λ-STIRAP的作用,所以在|3〉上必然存在一定的布居概率(P3,t如图2(d)内插图所示),它受γ的影响较4p方案要大一些.类似地,在4p方案中,中间能级之间以连续强光耦合发生跃迁,可以有效减小P3,t,降低η对γ的敏感程度从而提高效率.
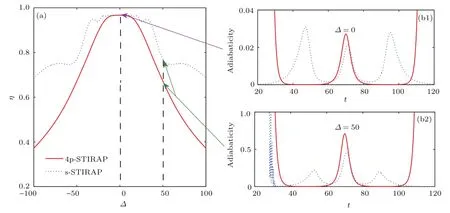
图3 (网刊彩色)(a)转移效率η随激发态失谐量Δ 的变化;(b1)和(b2)分别表征在Δ=0和Δ=50两处的绝热参数r(t);4p和s方案下的结果分别由红色实线和蓝色虚线表示;其他相关参数为Δt=7.8(s方案),γ=0.01Fig.3.(color online)(a)The transfer efficiency η as a function of detuning Δ;(b1),(b2)adiabaticity in the cases of Δ =0 and Δ =50.Results from 4p-STIRAP and s-STIRAP are presented by red solid and blue dashed lines,respectively.Other relevant parameters are Δt=7.8(s-STIRAP),γ =0.01.
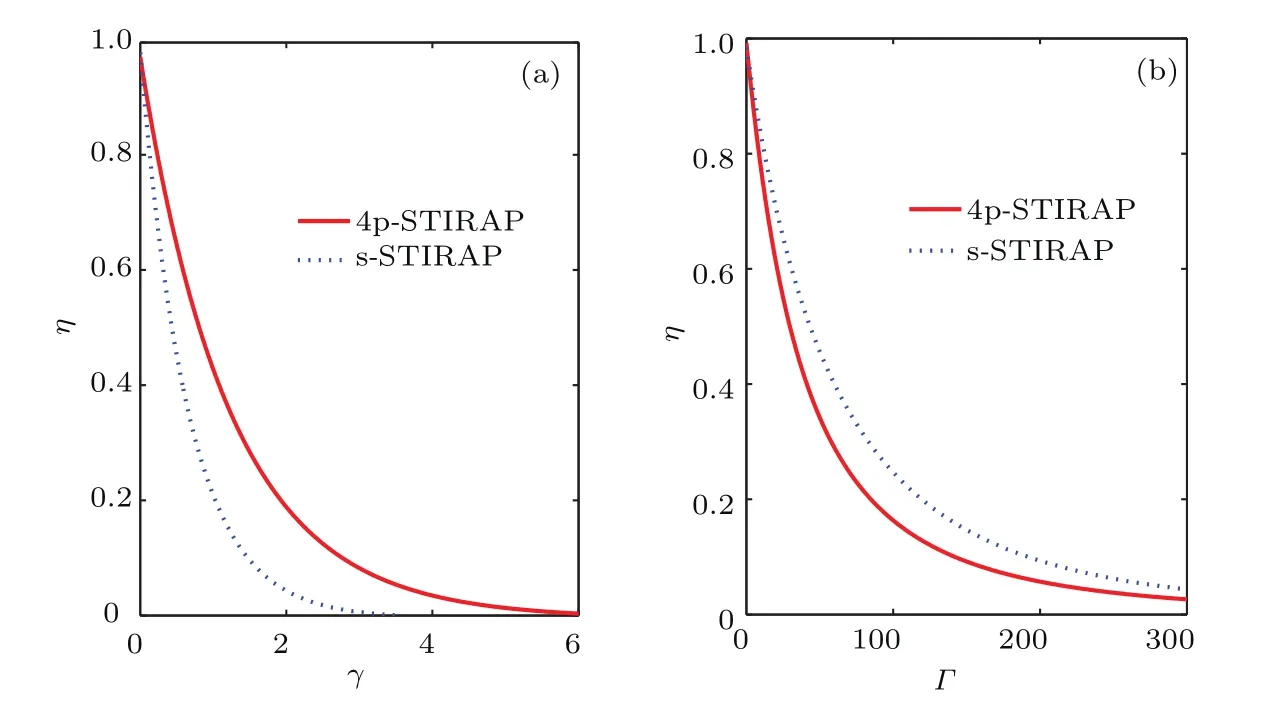
图4 (a)转移效率η随亚稳态自发辐射率γ的变化;(b)转移效率η随激发态自发辐射率Γ的变化;红色实线和蓝色虚线分别对应4p和s方案下的结果Fig.4.The variations of transfer efficiency η with(a)spontaneous decay rate γ of the metastable state and(b)spontaneous decay rate Γ of the excited states.Results from 4p-STIRAP and s-STIRAP are presented by red solid and blue dashed lines,respectively.
3)η4p(Γ)<ηs(Γ). 在s方案中,两对连续的逆序列激光脉冲对构成级联型STIRAP,分别用于实现|1〉→|3〉,|3〉→|5〉的布居数转移.脉冲对在各自的Λ-STIRAP中抑制了激发态上的布居,如|2〉上的布居被一对逆序列的Ω1和Ω2光脉冲作用所抑制.所以s方案受Γ的影响较4p方案略小,转移效率也较高.
4.3 激光脉冲幅值
从原理上来说,提高激光脉冲的幅值可直接促使能级之间耦合强度的增强,有效改善相干布居数的转移过程,因此,研究两种方案下光脉冲幅值的变化对布居转移的影响是非常必要的.鉴于两种方案下均存在四束激光,在模拟计算中做如下定义.
4p方案:令ε4p=,调节可改变比值ε4p,见图5(a)内插图所示.
s方案: 令εs=比值εs的调谐可以通过改变实现,见图5(b)插图所示.
图5(a)展示了4p方案下η4p-ε4p的关系曲线,取Ω0=100(蓝色实线)、10(红色虚线)、5(绿色点划线),发现随着ε4p从0.01增加到100,η4p的变化趋势相同,即先急速增加到峰值再缓慢减小.ε4p过大(ε4p≫1)或过小(ε4p≪1)都不易于布居数的转移,这表明实现效率最佳值要求脉冲幅值之比ε4p为1.0附近,此时数值相当,确保了Ω1(t)和Ω4(t)之间的部分重叠面积较合适.另一方面,增加幅值Ω0明显提高效率,满足η4p(Ω0=100)>η4p(Ω0=10)>η4p(Ω0=5).这是因为亮态本征态的能量正比于光脉冲的拉比频率,增大幅值能够有效抑制在亮态的布居数促使体系的动力学演化绝对符合准暗态的变化.这种解释对s方案也适用.所以,我们的结论是激光脉冲幅值Ω0对两种方案下的η都起到关键作用(Ω0与η成正关联),在Ω0给定的情况下,适当调谐比值ε4p可以获得η4p的最佳值.

图5 (网刊彩色)(a)4p方案中,η随ε4p的变化,蓝色实线、红色虚线和绿色点划线分别对应Ω0=100,10,5;(b)s方案中,η随εs和Δt的变化,Ω0=10;图(b)中白色虚线标注出不同幅值下实现最大转移效率所对应Δt的值;图(a)和(b)的内插图为激光的幅值示意图Fig.5.(color online)The relationship of η-ε4pis plotted in(a)with Ω0=100(blue solid),10(red dashed),5(green dash-dotted),and η in the space of(Δt,εs)is displayed in panel(b),here Ω0=10.The white dashed line in(b)points to exact Δt values when η attains its local maximum under different εsvalues.The insets of(a)and(b)show the amplitude of the lasers.
由于s方案下研究激光幅值的影响相对复杂,除脉冲幅值之比εs外脉冲对间的时差Δt也是重要的考虑参量.这里,假定绝对值Ω0=10不变,研究转移效率ηs与比值εs和时间Δt的依赖关系,结果见图5(b).发现,当εs(εs∈(0.1,100))和Δt(Δt∈(−30,30))同时变化时ηs随之变化,全局最大值ηs≈0.971出现在εs≈1.6,Δt≈8.2处,偏离该处都使得ηs明显减小.尤其是当Δt>20时ηs迅速减小为0,不依赖于εs的变化,原因是两个脉冲对之间重叠面积几乎为零,布居在经过第一个Λ-STIRAP后无法继续第二个Λ-STIRAP过程,最终经由态|3〉的自发辐射损失.图5(b)中白色虚线标注了给定εs值下ηs的局域最大值所对应Δt数值的轨迹,满足−10<Δt<10.因为该范围内激光脉冲对的重叠面积较合适,易实现布居的顺利转移.所以,与4p方案不同,s方案的关键是控制光脉冲对的时间间隔Δt,这是实现高效转移的必要条件.此外,选择合适的脉冲幅值之比εs在1.0附近有利于搜寻到ηs的全局最大值.
5 方案可行性分析与应用
5.1 实验可行性
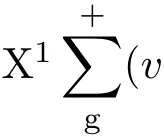
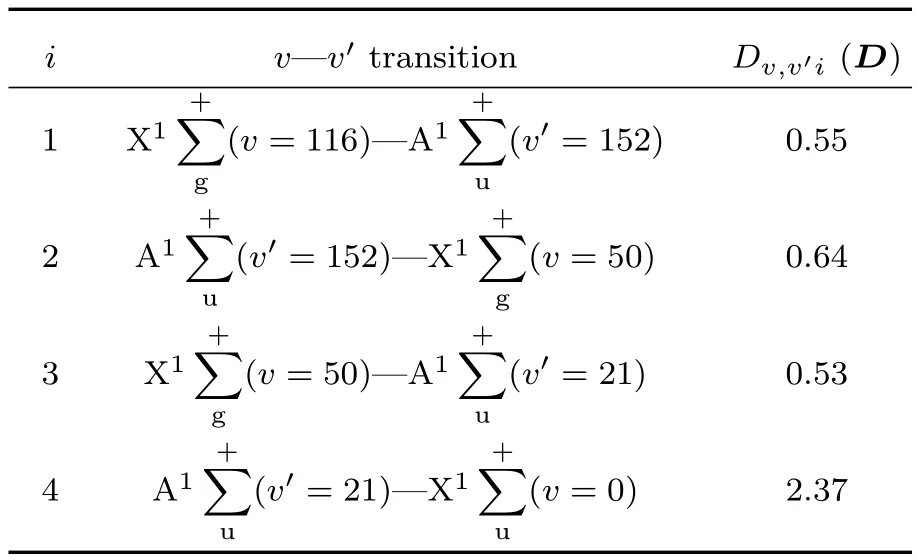
表1 87Rb2分子跃迁通道以及对应的电偶极矩Table 1.Energy levels for the transition and the corresponding dipole moments in87Rb2.
已知能级的自发辐射率分别为γ=6×104Hz,Γ=3×107Hz,光脉冲拉比频率的幅值均为根据光功率的表达式其中c为真空中的光速,ħ为普朗克常量.可计算实验上使用的激光幅值功率:I1~0.17 W/cm2,I2~0.13 W/cm2,I3~0.19 W/cm2和I4~0.01 W/cm2.因此求得4p(s)方案下实际的转移效率为:η4p≈0.473,ηs≈0.56(计算中激光的时序参数均取优化数值).此数值与实验文献[11]的结果较符合,却与理论预估的最佳值η~0.97相距甚远,主要原因是Γ的实际数值扩大了30倍(理论计算Γ=106Hz),导致一部分粒子布居经由激发态快速的自发辐射过程损失.解决问题的方法是选择更稳定的中间激发态能级,例如,里德伯分子能级.据目前实验测量里德伯分子能级寿命均在20µs左右(Γ~106Hz)[37,38],能够确保粒子布居的转移效率达0.90以上.
5.2 纠缠态的制备
纠缠态已被广泛应用于很多光学操控系统中,例如,利用STIRAP技术实现囚禁原子与单光子之间的纠缠[39],基于暗态在两原子系统中实现三态纠缠[40]等.由(5)式可知,约化后的准暗态|ω1〉≈sinβ|1〉+cosβ|5〉是可控纠缠态的标准形式.根据β的定义:β=arctan(Ω2Ω4/(Ω1Ω3)),调节激光脉冲幅值即可改变β的数值,不同的β值对应态|1〉,|5〉上不同的布居分配比,产生任意纠缠态.极限的情况下,当β=π/2或0时,|ω1〉≈|1〉或|ω1〉≈|5〉非纠缠;当β在(0,π/2)之间连续改变时,有望实现任意纠缠态的制备.
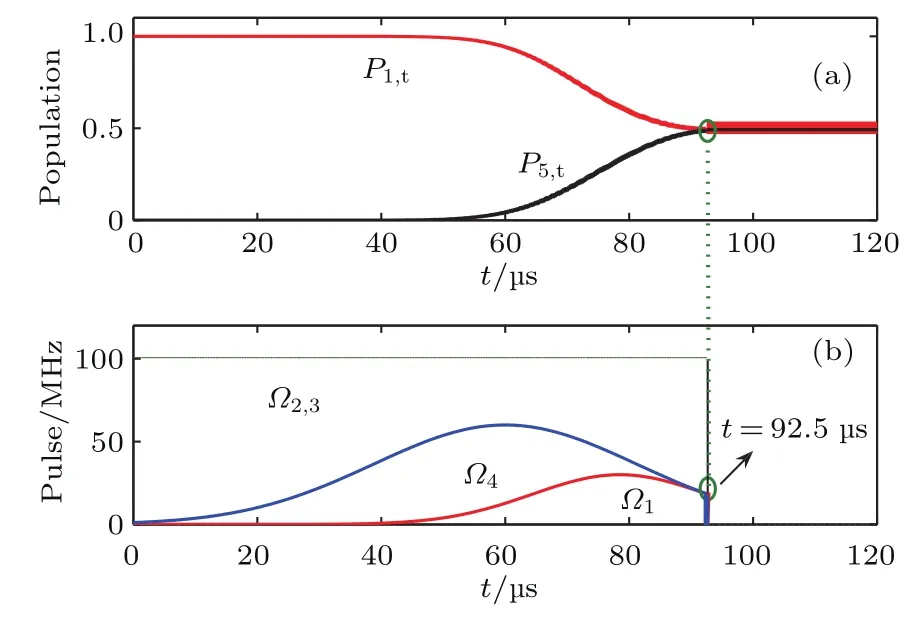
图6 (网刊彩色)(a)粒子布居数P1,t(红色)和P5,t(黑色)随时间演化的曲线,当t>92.5µs时,最终可实现粒子数的分布是P1,∞ =P5,∞ =0.5;(b)该过程所需的激光脉冲时序分布图;具体的激光参数为:Ω2=Ω3=100 MHz,Ωi(t)=exp[−(t−ti)2/(Ti)2] (i=1,4),其中,=30 MHz,=60 MHz,t1=78.5µs,t4=60µs,T1=20µs,T4=30µs;当t=92.5µs时,关闭所有激光,之后的布居数保持不变Fig.6. (color online)(a)Time-dependent population dynamics during the process of entangled state preparation.Populations P1,tand P5,tare respectively marked by red and black lines.The fi nal stable population distribution is P1,∞ =P5,∞ =0.5 after t=92.5µs.(b)The required light pulse sequences with laser parameters:Ω2=Ω3=100 MHz,Ωi(t)=exp[−(t−ti)2/(Ti)2](i=1,4)where=30 MHz,=60 MHz,t1=78.5 µs,t4=60µs,T1=20µs,T4=30µs.At t=92.5µs,all lasers are turned o ff,giving rise to stable population distributions.
下面举例说明如何产生最大纠缠态|ω1〉≈初始条件下,粒子完全制备在态|1〉上,即|ω1〉≈|1〉(P1,t=1.0). 若β从π/2调至π/4,便能实现P1,t=P5,t=0.5完成制备.由(4a)和(4b)式中α和β的定义可得(采用4p方案),假设Ω1和Ω4是一对下降沿部分重叠的高斯光,Ω2和Ω3是等幅的连续光且幅值远大于Ω1和Ω4.光脉冲的时序如图6(b)所示,具体的激光参数详见注释.初始情况P1,t=1.0,P5,t=0,粒子与激光场发生相互作用,当t=92.5µs时关闭所有激光,此时布居数恰好均匀分配在态|1〉和|5〉,使得P1,∞=P5,∞=0.5即得目标纠缠态|ω1〉. 图6(a)描绘了P1,t和P5,t随时间演化的关系曲线.
6 结 论
基于一个五能级级联系统,详细研究了4p(s)两种激光脉冲时序方案实现粒子布居高效转移的过程.通过解析求解系统的准暗态本征态和对应的绝热条件,详细讨论了各种实验参量包括激发态能级失谐量、中间能级的自发辐射率、激光脉冲的幅值以及光脉冲对之间的相对时差对转移效率的影响.研究重点旨在比较4p和s方案在实施过程的区别和各自优缺点,利用理论分析对实验结果进行解释和预测.研究发现,实验中观测到Cs2转移效率较低的主要原因是受激发态能级自发辐射率的影响,粒子在转移过程中无法绝对地绝热跟随准暗态,存在部分粒子因激发而损失的情况.
在两种方案的实际操作上,4p方案可控参量少,相对简单,对中间亚稳态能级自发辐射率的依赖程度小,缺点是准暗态的绝热性易受激发态能级失谐量的影响;s方案可控参量较多操作相对复杂,因为它依赖于两个Λ-STIRAP的级联,受中间亚稳态能级性质的影响较大,优点是绝热性相对稳定,不易受激发态能级失谐量的影响.除此之外,两种方案下都可以利用参量优化实现理论预期的最佳值η4p=ηs≈0.97.通过对方案的可行性和纠缠态制备的讨论,我们认为该STIRAP技术在目前的量子信息领域有一定的应用前景,如实现高保真度的量子可控纠缠态.因此下一步的研究目标可以放在继续拓展它们在量子信息、量子纠缠、精密测量相关领域的应用,也为实验上进一步探索超冷(极性)分子的产生方法提供了更多理论上的依据.
[1]Gaubatz U,Rudecki P,Schiemann S,Bergmann K 1990J.Chem.Phys.92 5363
[2]Vitanov N V,Rangelov A A,Shore B W,Bergmann K 2017Rev.Mod.Phys.89 015006
[3]Yun J,Li C,Chung H,Choi J,Cho M 2015Chem.Phys.Lett.627 20
[4]Vewinger F,Heinz M,Garcia-Fernandez R,Vitanov N V,Bergmann K 2003Phys.Rev.Lett.91 213001
[5]Toyoda K,Uchida K,Noguchi A,Haze S,Urabe S 2013Phys.Rev.A87 052307
[6]Qian J,Zhang W,Ling H Y 2010Phys.Rev.A81 013632
[7]Zhai J,Zhang L,Zhang K,Qian J,Zhang W 2015J.Opt.Soc.Am.B32 2164
[8]Di Stefano P G,Paladino E,Pope T J,Falci G 2016Phys.Rev.A93 051801
[9]Jamonneau P,Hétet G,Dréau,Roch J F,Jacques V 2016Phys.Rev.Lett.116 043603
[10]Yale C G,Buckley B B,Christle D,Burkard G,Heremans F J,Bassett L C,Awschalom D D 2013PNAS110 7595
[11]Danzl J G,Mark M J,Haller E,Gustavsson M,Hart R,Aldegunde J,Hutson J M Nägerl H C 2010Nat.Phys.6 265
[12]Chen T,Zhu S,Li X,Qian J,Wang Y 2014Phys.Rev.A89 063402
[13]Møller D,Sørensen J L,Thomsen J B,Drewsen M 2007Phys.Rev.A76 062321
[14]Webster S C,Weidt S,Lake K,McLoughlin J J,Hensinger W K 2013Phys.Rev.Lett111 140501
[15]Theuer H,Bergmann K 1998Eur.Phys.J.D2 279
[16]Kulin S,Saubamea B,Peik E,Lawall J,Hijmans T W,Leduc M,Cohen-Tannoudji C 1997Phys.Rev.Lett.78 4185
[17]Nölleke C,Neuzner A,Reiserer A,Hahn C,Rempe G,Ritter S 2013Phys.Rev.Lett.110 140403
[18]Novikov S,Sweeney T,Robinson J E,Premaratne S P,Suri B,Wellstood F C,Palmer B S 2015Nat.Phys.12 75
[19]Ospelkaus S,Pe’Er A,Ni K K,Zirbel J J,Neyenhuis B,Kotochigova S,Jin D S 2008Nat.Phys.4 622
[20]Ni K K,Ospelkaus S,de Miranda M H G,Pe’Er A,Neyenhuis B,Zirbel J J,Ye J 2008Science322 231
[21]Lang F,Winkler K,Strauss C,Grimm R,Denschlag J H 2008Phys.Rev.Lett.101 133005
[22]Stellmer S,Pasquiou B,Grimm R,Schreck F 2012Phys.Rev.Lett.109 115302
[23]Shore B W 2011Manipulating Quantum Structures Using Laser Pulses(Cambridge:Cambridge University Press)pp57–60
[24]Aikawa K,Akamatsu D,Hayashi M,Oasa K,Kobayashi J,Naidon P,Inouye S 2010Phys.Rev.Lett.105 203001
[25]Molony P K,Gregory P D,Ji Z,Lu B,Köppinger M P,Le Sueur C R,Cornish S L 2014Phys.Rev.Lett.113 255301
[26]Ji Z,Zhang H,Wu J,Yuan J,Yang Y,Zhao Y,Jia S 2012Phys.Rev.A85 013401
[27]Park J W,Will S A,Zwierlein M W 2015Phys.Rev.Lett.114 205302
[28]Guo M,Zhu B,Lu B,Ye X,Wang F,Vexiau R,Wang D 2016Phys.Rev.Lett.116 205303
[29]Ciamei A,Bayerle A,Chen C C,Pasquiou B,Schreck F 2017Phys.Rev.A96 013406
[30]Liao W T,Pál ff y A,Keitel C H 2011Phys.Lett.B705 134
[31]Oreg J,Bergmann K,Shore B W,Rosenwaks S 1992Phys.Rev.A45 4888
[32]Viteau M,Chotia A,Allegrini M,Bouloufa N,Dulieu O,Comparat D,Pillet P 2008Science321 232
[33]Klein J,Beil F,Halfmann T 2007Phys.Rev.Lett.99 113003
[34]Du Y X,Liang Z T,Huang W,Yan H,Zhu S L 2014Phys.Rev.A90 023821
[35]Pu H,Maenner P,Zhang W,Ling H Y 2007Phys.Rev.Lett.98 050406
[36]Meystre P 2001Atom Optics(New York:Springer Science&Business Media)pp4–7
[37]Butscher B,Bendkowsky V,Nipper J,Balewski J B,Kukota L,Löw R,Rost J M 2011J.Phys.B:At.Mol.Opt.Phys.44 184004
[38]Bendkowsky V,Butscher B,Nipper J,Sha ff er J P,Löw R,Pfau T 2009Nature458 1005
[39]Volz J,Weber M,Schlenk D,Rosenfeld W,Vrana J,Saucke K,Weinfurter H 2006Phys.Rev.Lett.96 030404
[40]Zhen B Y,Huai Z W,Shi B Z 2010Chin.Phys.B19 094205
PACS:33.80.Be,42.50.Hz,32.80.Rm,42.65.Dr DOI:10.7498/aps.66.213301
*Project supported by the National Natural Science Foundation of China(Grant Nos.11474094,11104076).
†Corresponding author.E-mail:jqian1982@gmail.com
Theoretical research on an efficient population transfer based on two different laser pulse sequences∗
Zhang Lu Yan Lu-Yao Bao Hui-Han Chai Xiao-Qian Ma Dan-Dan Wu Qian-Nan Xia Ling-Chen Yao Dan Qian Jing†
(Quantum Institute for Light and Atoms,Department of Physics and Material Science,East China Normal University,Shanghai 200062,China)
d 23 May 2017;revised manuscript
11 July 2017)
A quantum gas of ultracold molecules,with long-range and anisotropic interactions,will enable a series of fundamental studies in physics and chemistry.In particular,samples of ground-state molecules at ultralow temperatures and high number densities will facilitate the explorations of a large number of many-body physical phenomena and applications in quantum information processing.However,due to the lack of efficiently cooling techniques such as laser cooling for atomic gases,high number densities for ultracold molecular samples are not readily attainable.Associating ultracold atoms to weakly bound dimer molecules via Feshbach resonance and subsequently transferring them to a wanted molecular ro-vibronic ground state by a stimulated Raman adiabatic passages(STIRAP)have proved to be an effective way in producing ideal ultracold molecular samples.As a typical illustration,in a recent study(2010Nat.Phys.6 265)Danzl et al.experimentally realized the preparation of Cs2molecule into its ro-vibronic ground state via two different multi-level STIRAPs:one is based on a single conversion route and the others are based on a cascade-connected route(labeled by 4p-STIRAP and s-STIRAP,respectively).In this work,we present a theoretical study for these two STIRAP schemes,focusing on the di ff erences in physical principle and realistic performance between them.On the one hand,according to the theoretical approach of quasi-dark eigenstates,we conclude that a highly efficient population transfer is achievable in both schemes.On the other hand,by systematically studying the in fluences of the relevant parameters,including the spontaneous decays and the detunings from the intermediate states,and the temporal sequence and the amplitude of the laser pulses,we disclose their respective advantages and weaknesses in the realistic implementation.We theoretically predict that for both schemes their maximal conversion efficiencies each can attain 0.97 as long as the spontaneous decays from the intermediate excited states are sufficiently suppressed.Yet considering the fact that the already implemented efficiency is only around 0.6 for both schemes,there is still room for optimization,e.g.using stable Rydberg energy levels in future experiment.Furthermore,the success of these two schemes can provide a new route to the controllable entanglement preparation,opening more applications in the fields of quantum logic gate and so on.
stimulated Raman adiabatic process,population transfer,adiabatic condition,entangled state
基于最近实验工作的结果(2010Nat.Phys.6 265)即Danzl等在五能级M型级联系统中分别利用连续型和四光子型受激拉曼绝热通道(stimulated Raman adiabatic passage,STIRAP)实现了将Feshbach态上弱束缚的Cs2有效转移到其振转基态,本文理论研究了两种STIRAP方案实施的基本条件,解析推导系统的准暗态、绝热参数的具体形式并分析其存在的必要性,详细讨论布居转移效率对相关参量的依赖关系.通过比较激光脉冲的时序、中间能级的失谐量和自发辐射率、光场脉冲的幅值等诸多参量的不同影响,讨论方案各自的优缺点,找到了参量优化的方法以实现最高效的粒子布居数转移.与前人的实验结果相比,本文研究表明,实验观测值(约0.60)均低于理论预估最佳值(约0.97)的主要原因是受限于激发态能级的自发辐射率过大.该理论方案还可用于制备量子纠缠态,在量子逻辑门操控、量子信息传输等领域都有潜在的应用.
10.7498/aps.66.213301
∗国家自然科学基金(批准号:11474094,11104076)资助的课题.
†通信作者.E-mail:jqian1982@gmail.com
©2017中国物理学会Chinese Physical Society
