基于投入产出法的全要素生产率评估研究

张海伟，李 平

(山东理工大学 经济学院，山东 淄博 255000)

基于投入产出法的全要素生产率评估研究

张海伟，李 平

(山东理工大学 经济学院，山东 淄博 255000)

以40个国家1995—2011年的数据为样本，运用投入产出法测算全要素生产率，并将结果与采用传统生产要素测算的原始结果进行比较，表明运用投入产出法测得全要素生产率明显低于原始结果，主要原因是技术效率存在高估；前者测算结果相对平稳，且当全要素生产率变动较大时，两种结果也相差较大；运用DEA测算方法可得到发展中国家与发达国家技术差距逐渐收敛的结论。

投入产出法；全要素生产率；DEA

一、引言

1957年，Solow提出全要素生产率(TFP)概念后便引起学术界高度关注，TFP至今仍是衡量一国GDP、经济增长和经济波动的重要指标。然而，TFP测算法始终没有得到一致认可。学者对TFP测算的质疑使该指标衡量一国或地区经济发展水平的可靠性下降，测算结果对经济现实的说服力不足，合理的测算方法显得尤为重要。目前，学界对TFP测度的质疑主要在现实条件是否满足计量模型核算的前提假设及生产要素数据测算是否存在误差等。比如作为TFP衡量的重要指标，GDP存在数据失真、折算不准确等被高估情况，成为TFP测算结果偏大的因素之一。

针对以上不足，学者纷纷提出对TFP测算的改进方法。除找到具有权威性和准确性的测量方法外，尽量减少投入要素数据测算误差，是减少TFP测量偏误的重中之重。目前关于TFP测量数据改进和处理的文献很多，遗憾的是现有研究对于数据选取和折算仍然无法统一。具体表现为：在资本存量估算改进的文献中，学者对使用资本的界定和盘存方法各持己见[1]369-401；在劳动力改进的文献中，劳动质量的衡量指标存在差异，如何实现数据选取和折算统一成为我们研究的重点。Jorgenson和Nishimizu(1978)提出基于国民经济核算上的KLEMS方法，将投入产出法与TFP相联系，给我们研究提供了思路。我们认为相对于传统数据选取和计算方法不统一的缺陷，利用世界投入产出表中数据作为编制国民收入的重要部分，能够使各个国家的投入有统一衡量标准，减少数据偏差。同时，相比传统生产要素投入，以货币化衡量的生产投入能更好地考虑要素质量问题，从而有效地解决现有数据测量偏误问题。

基于此，我们重点采用投入产出数据对各国TFP进行测算。文章的创新点在于避开“改进资本、劳动等有形生产要素测算来完善TFP”的传统思路，将世界投入产出表中各个国家作为投入中间品生产的决策部门，建立一个系统完整的投入产出框架，用货币化的中间品投入代替单纯的要素投入数量，由中间品的投入总量和配置方法决定一个国家的技术进步率。与传统测量方法相比，我们所用方法不仅可以避免不同数据选取的误差，还可以综合考虑国内外投入要素的质与量，在全球价值链的基础上衡量内涵与外延的技术进步。根据我们测度方法，如果一个国家的实际产出和潜在产出相一致，我们可认为这个国家的技术是有效的，否则视为无效。进一步将最终结果与普通测算TFP方法的所得结果进行对比，从中验证它们之间的吻合程度及差别，并探寻其测算差异的原因。

二、研究方法

目前，TFP测算方法主要分为参数估计法和非参数估计法两种。参数估计法主要包括收入配额法、计量经济学方法和随机边界法，它们均涉及参数函数估计，并假设研究对象在技术上是有效的。非参数估计方法主要包括数据包络法(Data Envelopment Analysis，即DEA)和指数法等不涉及参数函数估计，也不需要假设技术有效[2]56-64。通过表1我们可以看出，各种衡量TFP的估计方法都有使用的局限性。数据包络法虽然可能使得每个决策单元缺乏可比性，却具有简明性、应用性和易操作性强等特点，得到广泛应用。针对TFP的数据特征，采用数据包络(DEA)测算方法对投入产出数据进行测度进而评估TFP是相对合适的。

表1 TFP不同测算方法的比较

类别估计方法存在的弊端参数估计法收入配额法资本盘存困难，没有考虑投入要素质量问题计量经济学方法生产要素无法准确估计，技术进步与全要素生产率无法剥离随机边界法投入指标存在相关性时，易产生偏差非参数估计法DEA每个决策单元的特性缺乏可比性指数法难以确定企业的技术生产结构，使得指数选取偏离实际生产结构

在操作过程中，我们选择将世界投入产出表中的中间产品作为投入指标，其主要原因在于：第一，不限制投入要素数量与种类。传统TFP测算方法对投入的生产要素考虑不够全面，在进行实证检验过程中，更多利用的是资本、就业等有限生产要素，但事实上生产产品所用的生产要素多种多样，在测算过程中投入要素不可能罗列穷尽，而投入产出法在全球价值链的基础上将中间品作为投入指标，综合考虑国内外投入要素情况，不再涉及投入要素的种类和数量问题，相对于生产要素数量投入而言更为精确和贴近现实。第二，综合考虑到内涵和外延的技术进步。传统TFP测算方法无法同时测算内涵和外延技术进步。内涵的技术进步又包括两种：一种是各个生产要素的数量不变，质量发生变化；另一种是生产要素与生产要素之间的组合变得更完美。而外延的技术进步则考虑生产要素的量而非质。如今大多数研究者采用的是利用就业人数、资本存量等进行测算，劳动的质量被忽略[3]16-35，这说明生产要素投入分析的仅仅是外延技术进步，测算结果有很大偏差。而投入产出法中货币化的中间产品投入，可以综合考虑投入要素的质与量，即同时考虑到内涵与外延的技术进步。第三，避免使用数据不一致。传统TFP测算方法数据来源不一致和计算方法不统一使得计量结果出现偏差，而利用投入产出法则可避免采用资本盘存等不真实数据核算，且数据均出自同一种处理方法，减小了误差。因此，相比传统测算方法，利用投入产出法测算的TFP更真实，且TFP测算过程中存在投入要素遗漏、忽视要素投入质等问题可能导致测度结果夸大。根据以上推断我们可以得出初步结论：传统测量结果存在一定误差，会使TFP被高估。为了验证我们的观点，进一步进行实证检验。

三、模型选取与数据说明

(一)模型选取

由于投入产出法假定每个产品部门只生产一种同质产品，不同产品部门的产品之间不能相互替代，并且对于任何一个部门而言，其投入与产出为正比例变动关系，收益增加速度等于规模扩大的幅度，这一假定保证了各个部门生产规模报酬的不变性。因此，我们把投入量作为基本决策变量，选择投入导向并且规模报酬不变的CRS模型。在利用CRS模型测算技术效率得分后，进一步利用Malmquist模型计算全要素生产率变动、技术变动以及技术效率变动等指数。

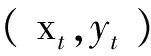
(二)数据处理

1.世界投入产出数据

我们采用WIOT中提供的1995—2011年世界投入产出数据，鉴于其最早年份为1995年，我们择取1995年为基期，研究美国、日本、韩国、中国、俄罗斯等世界投入产出表中列出的40个国家。Cooper等(2000)指出，DEA对所有决策单元投入与输出数据必须为正数，而利用投入产出表中数据不可避免存在许多0值现象，因此，必须对投入数据进行非负处理[4]1-25。结合DEA特点即各个决策单元的同一指标数据同时加上相同的正数或者适当减去相同的正数(aj,bj)>0时，其DEA有效性不变。已有许多文献利用该特点对其数据进行处理。例如，崔晓东和郑玉华(2011)对数据的非负处理是对该项投入或产出直接加上一个常数[5]72-78。我们在此基础上，利用数据归一的原理，将投入产出表中的数据处理在 0，1 之间，以此满足DEA对数据的要求。

2.资本存量及其他变量

由于我们的目的是比较利用投入产出法和传统方法测算全要素生产率，因此各国总产出、资本存量和劳动投入是DEA模型分析中所必须选择的三个变量。我们以各国GDP来表示总产出，为消除价格影响，选用2005年不变美元计价的实际GDP；劳动投入以各国就业人数来表示；各国1995—2011年的资本存量则使用Goldsmith(1951)开创的永续盘存法来估计资本存量。

四、测算结果与分析

(一)CRS结果比较

我们测算了1995—2011年40个国家的全要素技术效率得分，由于数据较多，所以仅列出最后3年及各国均值进行比较，结果如表2。其中，DEA1和DEA2分别表示用投入中间品和投入生产要素测得的技术效率得分(以下均用DEA1和DEA2表示投入中间产品与投入生产要素后的结果)。

由表2看到，总体来说，DEA1效率得分普遍小于DEA2，DEA1的总平均值0.67小于DEA2测得的0.717，说明用生产要素测得的技术效率普遍高于中间产品投入测得的技术效率。具体而言：首先，对于各个国家，DEA1小于DEA2的国家占72.5%，仅有27.5%的国家不符合预期。其次，从时间角度看，2009、2010、2011年各年平均测得的DEA1均小于DEA2，并且它们之间的差距是逐年增加的，高于总的平均差距，说明这三年各个国家技术效率相对之前几年有较大提升，且DEA2提升的幅度高于DEA1。最后，从波动幅度来看，DEA1总体标准差0.181小于DEA2测得的0.189，说明总体DEA1数据稳定性高于DEA2。

(二)Malmquist指数测算

通过CRS测算可以得到各个国家历年技术效率得分情况，但是数据波动较大，不容易得出可比较总结的规律，因此进一步利用Malmquist指数将全要素生产率变动分解并利用其测得的均值来说明问题，具体结果见表3。

表3给出了从1995到2011年全要素生产效率指数的均值，可以看出，DEA1与DEA2测得的技术效率变动与技术进步变动率存在不一致性。第一，DEA1测得的技术效率变动普遍小于DEA2测得结果。除德国、法国、意大利、日本和台湾地区外，其余35个国家技术变动效率均表现为DEA1小于DEA2，说明绝大多数国家普遍存在技术效率高估现象；第二，DEA1与DEA2测得的各国技术进步变动指数大小关系不容易总结。值得注意的是：在40个国家中，有6个国家利用不同方法测算的技术进步变动一致，有18个国家测得的指数是DEA1大于DEA2，其余16个国家测得的是DEA1小于DEA2，但是两种方法测算出来的数据差距很小，这一点可以从总均值中更好体现出来，其两种方法总均值为DEA1= DEA2=1.009，两者持平，说明两种方法测算的技术进步变动差距不明显，这有助于我们找到TFP被夸大的源头；第三，DEA1测得TFP变动普遍小于DEA2测得结果，除意大利、立陶宛和台湾地区外，其余37个国家均存在TFP被高估。此外，针对DEA1与DEA2分别测得的技术进步指数与技术效率指数来看，技术进步指数普遍大于技术效率指数，说明TFP的提升主要依靠的是技术进步，这与许多学者的观点一致[6]31-35。综上所述，虽然技术进步是提升TFP的主要原因，但是TFP被高估的原因却主要在于各个国家的技术效率在一定程度被高估。

表2 2009—2011年世界各国全要素技术效率得分

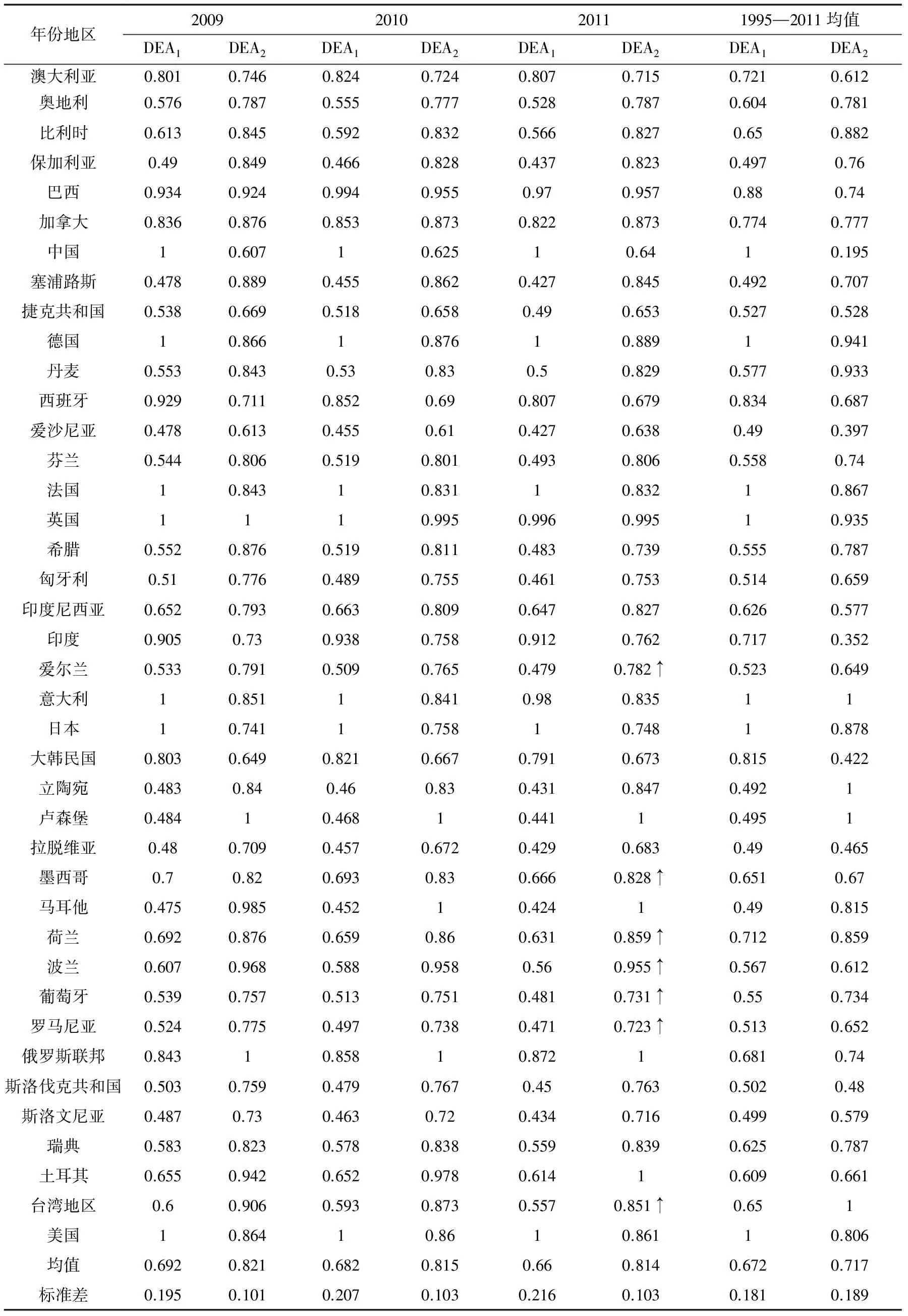
年份地区2009201020111995—2011均值DEA1DEA2DEA1DEA2DEA1DEA2DEA1DEA2澳大利亚0．8010．7460．8240．7240．8070．7150．7210．612奥地利0．5760．7870．5550．7770．5280．7870．6040．781比利时0．6130．8450．5920．8320．5660．8270．650．882保加利亚0．490．8490．4660．8280．4370．8230．4970．76巴西0．9340．9240．9940．9550．970．9570．880．74加拿大0．8360．8760．8530．8730．8220．8730．7740．777中国10．60710．62510．6410．195塞浦路斯0．4780．8890．4550．8620．4270．8450．4920．707捷克共和国0．5380．6690．5180．6580．490．6530．5270．528德国10．86610．87610．88910．941丹麦0．5530．8430．530．830．50．8290．5770．933西班牙0．9290．7110．8520．690．8070．6790．8340．687爱沙尼亚0．4780．6130．4550．610．4270．6380．490．397芬兰0．5440．8060．5190．8010．4930．8060．5580．74法国10．84310．83110．83210．867英国1110．9950．9960．99510．935希腊0．5520．8760．5190．8110．4830．7390．5550．787匈牙利0．510．7760．4890．7550．4610．7530．5140．659印度尼西亚0．6520．7930．6630．8090．6470．8270．6260．577印度0．9050．730．9380．7580．9120．7620．7170．352爱尔兰0．5330．7910．5090．7650．4790．782↑0．5230．649意大利10．85110．8410．980．83511日本10．74110．75810．74810．878大韩民国0．8030．6490．8210．6670．7910．6730．8150．422立陶宛0．4830．840．460．830．4310．8470．4921卢森堡0．48410．46810．44110．4951拉脱维亚0．480．7090．4570．6720．4290．6830．490．465墨西哥0．70．820．6930．830．6660．828↑0．6510．67马耳他0．4750．9850．45210．42410．490．815荷兰0．6920．8760．6590．860．6310．859↑0．7120．859波兰0．6070．9680．5880．9580．560．955↑0．5670．612葡萄牙0．5390．7570．5130．7510．4810．731↑0．550．734罗马尼亚0．5240．7750．4970．7380．4710．723↑0．5130．652俄罗斯联邦0．84310．85810．87210．6810．74斯洛伐克共和国0．5030．7590．4790．7670．450．7630．5020．48斯洛文尼亚0．4870．730．4630．720．4340．7160．4990．579瑞典0．5830．8230．5780．8380．5590．8390．6250．787土耳其0．6550．9420．6520．9780．61410．6090．661台湾地区0．60．9060．5930．8730．5570．851↑0．651美国10．86410．8610．86110．806均值0．6920．8210．6820．8150．660．8140．6720．717标准差0．1950．1010．2070．1030．2160．1030．1810．189

表3 Malmquist分解的指数均值

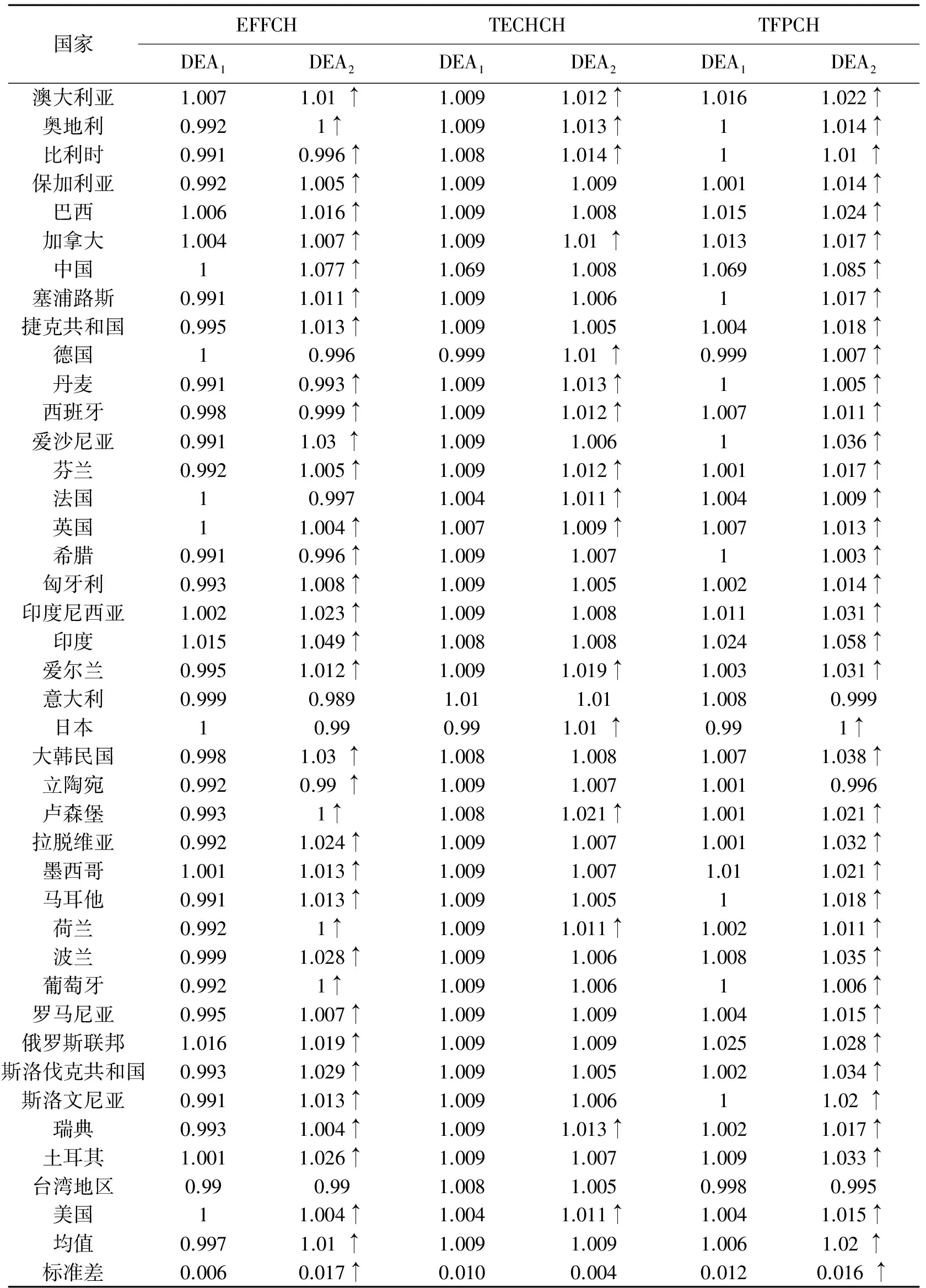
国家EFFCHTECHCHTFPCHDEA1DEA2DEA1DEA2DEA1DEA2澳大利亚1．0071．01↑1．0091．012↑1．0161．022↑奥地利0．9921↑1．0091．013↑11．014↑比利时0．9910．996↑1．0081．014↑11．01↑保加利亚0．9921．005↑1．0091．0091．0011．014↑巴西1．0061．016↑1．0091．0081．0151．024↑加拿大1．0041．007↑1．0091．01↑1．0131．017↑中国11．077↑1．0691．0081．0691．085↑塞浦路斯0．9911．011↑1．0091．00611．017↑捷克共和国0．9951．013↑1．0091．0051．0041．018↑德国10．9960．9991．01↑0．9991．007↑丹麦0．9910．993↑1．0091．013↑11．005↑西班牙0．9980．999↑1．0091．012↑1．0071．011↑爱沙尼亚0．9911．03↑1．0091．00611．036↑芬兰0．9921．005↑1．0091．012↑1．0011．017↑法国10．9971．0041．011↑1．0041．009↑英国11．004↑1．0071．009↑1．0071．013↑希腊0．9910．996↑1．0091．00711．003↑匈牙利0．9931．008↑1．0091．0051．0021．014↑印度尼西亚1．0021．023↑1．0091．0081．0111．031↑印度1．0151．049↑1．0081．0081．0241．058↑爱尔兰0．9951．012↑1．0091．019↑1．0031．031↑意大利0．9990．9891．011．011．0080．999日本10．990．991．01↑0．991↑大韩民国0．9981．03↑1．0081．0081．0071．038↑立陶宛0．9920．99↑1．0091．0071．0010．996卢森堡0．9931↑1．0081．021↑1．0011．021↑拉脱维亚0．9921．024↑1．0091．0071．0011．032↑墨西哥1．0011．013↑1．0091．0071．011．021↑马耳他0．9911．013↑1．0091．00511．018↑荷兰0．9921↑1．0091．011↑1．0021．011↑波兰0．9991．028↑1．0091．0061．0081．035↑葡萄牙0．9921↑1．0091．00611．006↑罗马尼亚0．9951．007↑1．0091．0091．0041．015↑俄罗斯联邦1．0161．019↑1．0091．0091．0251．028↑斯洛伐克共和国0．9931．029↑1．0091．0051．0021．034↑斯洛文尼亚0．9911．013↑1．0091．00611．02↑瑞典0．9931．004↑1．0091．013↑1．0021．017↑土耳其1．0011．026↑1．0091．0071．0091．033↑台湾地区0．990．991．0081．0050．9980．995美国11．004↑1．0041．011↑1．0041．015↑均值0．9971．01↑1．0091．0091．0061．02↑标准差0．0060．017↑0．0100．0040．0120．016↑

为进一步阐释基于两种测算方法下各国TFP的不一致性，我们将比较1995—2011年DEA1与DEA2所测数据的动态变化，以1995年为基期，Malmquist生产率指数连乘，可以得到历年相对于1995年累积全要素生产率的变化。如图1所示，可以看出历年DEA1均位于DEA2下方，表示DEA1测得的指数均小于DEA2，再次证实使用生产要素投入测算的结果是被高估的。观察数据走势可得，在1995—2000年，二者差距较大，主要原因是1998年金融危机发生，DEA2一直呈现上升趋势，而DEA1则出现明显下降，表明该次金融危机对DEA1的影响大于对DEA2的影响，极大影响了各国新技术的运用效率。在2000年之后，两者变动方向基本一致。值得注意的是，在2008—2010年，DEA1与DEA2均出现下降，DEA1下降的幅度小于DEA2，说明2008年的金融危机对生产要素投入的影响较大，极大影响了各国新技术的研发。此外，从数据波动的情况看，可以看出DEA1比DEA2增长的更平缓。具体表现为：在2001—2008年，两者均呈上升趋势，并且DEA2比DEA1增长速度更快；在2009—2010年，DEA1与DEA2均出现下降情况，同样DEA2下降的幅度明显超过DEA1。由图1，我们进一步验证了通过表2得到的结论，即DEA2在一定程度上夸大了全要素生产率的变动，并且DEA1测得的数据比DEA2更稳定。

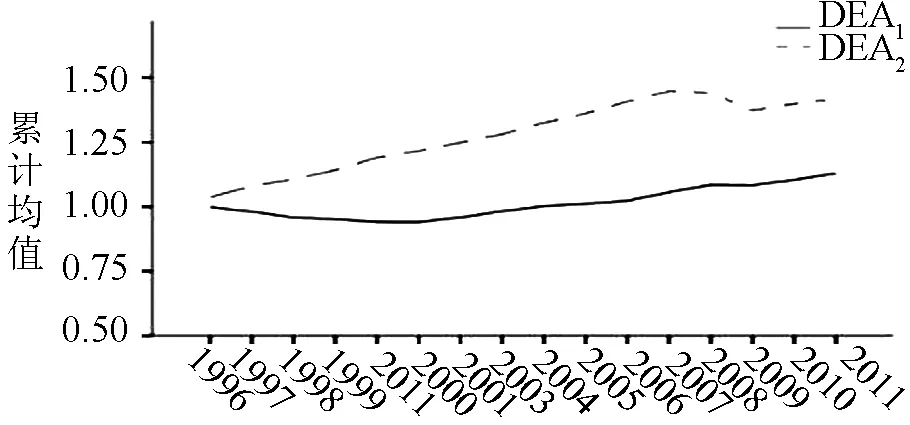
图1 1995-2011累计Malmquist生产率指数均值

为进一步验证DEA1与DEA2测算结果在各国家、地区的差别，可以根据两种方法测算得到的结果对国家地区进行排名，来分析两种方法的差距。具体操作是将两种方法测得40个国家和地区的平均TFP排名，并列出排名前十位与排名后十位的国家或地区，以方便分析比较。如表4所示，在排名前十位的国家中，DEA1与DEA2测得结果均在前十位的国家共有5个，其中，排名一致的有1个为印度尼西亚；在排名后十位的国家中，DEA1与DEA2均出现的国家共有7个，并且排名一致的有4个，分别为印度、斯洛文尼亚、波兰和法国。通过对比分析，我们可以看出，在排名后十位的国家中，DEA1与DEA2之间的排名情况差距较小，而对于排名前十位的国家，DEA1与DEA2之间的差距较大。这说明，TFP变动率越大的国家，DEA1与DEA2的差异越大，其可能是受到影响TFP变动的外部因素，使得该国家投入生产要素与中间产品出现较大差距。

表4 各国TFP变动率均值排名

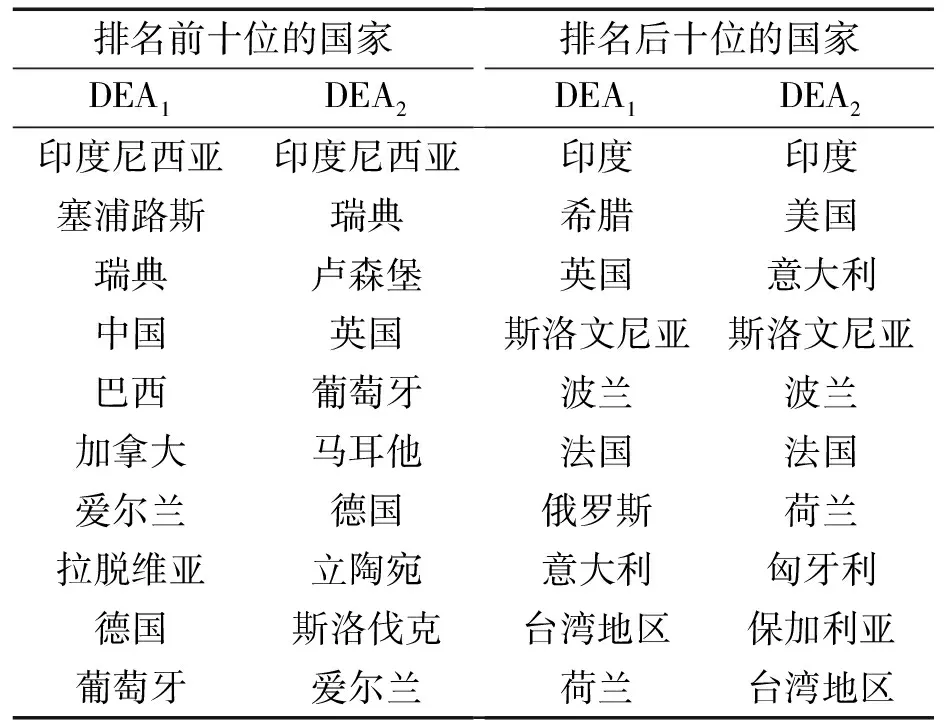
排名前十位的国家排名后十位的国家DEA1DEA2DEA1DEA2印度尼西亚印度尼西亚印度印度塞浦路斯瑞典希腊美国瑞典卢森堡英国意大利中国英国斯洛文尼亚斯洛文尼亚巴西葡萄牙波兰波兰加拿大马耳他法国法国爱尔兰德国俄罗斯荷兰拉脱维亚立陶宛意大利匈牙利德国斯洛伐克台湾地区保加利亚葡萄牙爱尔兰荷兰台湾地区

(三)对发达国家与发展中国家TFP变动的对比

技术进步是世界经济增长的重要因素，是提高一国软实力的重要保证，在对各国经济分析的过程中，技术进步是不可忽略的因素。通过上述验证，我们将投入产出法结合DEA的测度方法具有可信度。用该方法测度的结果表明，现有TFP存在明显高估和不准确的情况。结合现实情况可知，任何国家与地区都不能仅仅依靠自身力量进行科技创新，衡量各个国家TFP更不可以局限于国内有限的生产要素方面。在全球价值链日益升级优化的同时，索罗余值等测算方法仅仅考虑到本国投入的生产要素质与量，测量结果应存在高估，相对而言，DEA1方法利用投入产出法，综合考虑生产一种产品所需要的各个国家中间产品投入。这不禁引发新的思考，传统方法测度发达国家和发展国家技术差距是否可信？为解决该问题，我们进一步将40个国家进行分类比较，测算颇具争议的发达国家与发展中国家TFP差距问题。

为使测算结果更加准确，我们利用投入产出表中各个国家和地区总投入与总产出的权重，加权核算发达国家与发展中国家的TFP变动。如图2和图3所示，利用DEA1得到的发达国家与发展中国家TFP变动的差距有逐渐减小的趋势，这与李平、随洪光(2006)的观点相吻合[7]50-59，而DEA2测得的结果却与之相反。可见，DEA2不仅夸大了各国TFP，同时夸大发达国家与发展中国家之间技术进步率的差距。值得注意的是，无论用哪种方法，测得的发达国家TFP变动均位于发展中国家下方，表明近年发达国家的技术进步速度低于发展中国家。但DEA1与DEA2不同的是：第一，DEA1测得发达国家在2008年TFP变动是小于1的，说明在2008年之前，历年TFP有不同程度下降，而发展中国家TFP变动则在1附近波动；第二，发达国家与发展中国家在2001年TFP均值开始上升，可能的原因是部分国家加入WTO，有利于提升该国的TFP水平，且这一变化对发达国家影响较大，具体表现为TFP变动率突然增大，但是仍未突破1。因此，正是由于1996-2008年之间发达国家TFP下降与发展中国家TFP上升，才导致发达国家与发展中国家TFP差距呈逐渐减小趋势。相反，对于DEA2的结果，可以看出，在2000年之前，发达国家TFP变动小于1与发展中国家TFP变动大于1在一定程度上起到缩小TFP差距的作用，在2000年之后，发达国家与发展中国家都以稳定的比率逐年上升，因此，发展中国家与发达国家TFP差距越来越大。

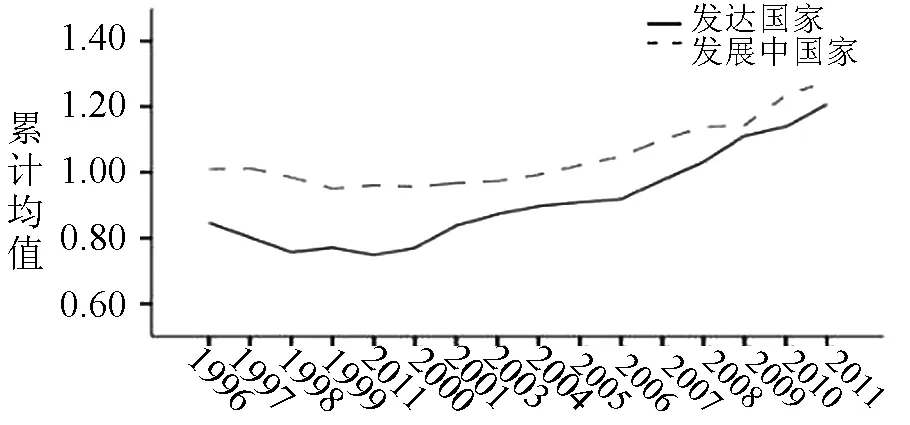
图2 DEA1测得发达国家与发展中国家

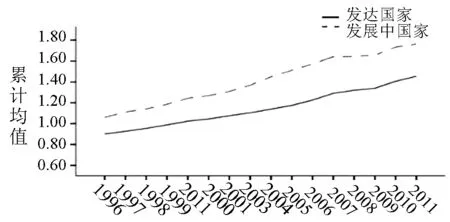
图3 DEA2测得发达国家与发展中国家

五、结论

我们采用投入产出法与DEA方法分析1995—2011年40个国家和地区TFP的变动，以期提供更为真实的结果。研究结论如下：第一，利用CRS模型得到历年平均技术效率得分情况，用投入产出法测得的TFP普遍小于用生产要素投入测得的TFP，且前者稳定性高于后者；第二，将Malmquist生产指数分解得到的TFP变动指数、技术效率指数与技术进步指数进行对比可得，用生产要素投入数量测算的TFP存在一定程度高估，其主要原因在于技术效率被高估，这说明传统方法可衡量的投入要素数量有限，在产出一定的情况下，最小化投入的能力被夸大。同时，将Malmquist生产指数连乘，同样可以看出历年TFP变动均呈现DEA1小于DEA2；第三，通过DEA1与DEA2测得结果对国家和地区进行排名，可以看出前十名的国家吻合度较差，后十名的国家吻合度较高，由此得出TFP变动率越大的国家，两种测算方法测算的差距越大；第四，对DEA1与DEA2结果分类处理，发现发达国家与发展中国家的技术差距是逐渐减小的。减小的原因在于在相当一段时间内，发达国家技术进步率呈现下降趋势，给发展中国家追赶的机会和空间。

根据测算结果分析，我国同样存在TFP被高估情况。DEA1测得的TFP变动为1.069，小于DEA2测得的1.085，同时技术效率变动也被高估(前者为1，后者为1.077)且在40个国家和地区中高估程度相对较高，探究TFP被高估的深层原因尤为重要。考虑到我们测算方法的局限性，即鉴于DEA的局限性，只能将世界投入产出表中各个行业层次整合为国家层次进行测算，无法提供一个国家TFP更详尽的信息。因此，在下一步研究中，宜将针对中国的投入产出数据，测算具体行业的TFP变动，检测我国TFP真实水平并探寻其提升路径，为我国全面提高全要素生产率水平提供决策参考。

[1]Marrocu E, Paci R. Education or Creativity: What Matters Most for Economic Performance?[J]. Economic Geography, 2012, 88(4).

[2]李小平，朱钟棣．中国工业行业的全要素生产率测算——基于分行业面板数据的研究[J].管理世界，2005，(4)．

[3]Oyeranti A. Concept and Measurement of Productivity. Productivity and Capacity Building in Nigeria[C].Proceedings of the Ninth Annual Conference of the Zonal Research Units of the Central Bank of Nigeria，2000.

[4]Cooper W, Seiford M, Zhu J. A Unified Additive Model Approach for Evaluating Inefficiency and Congestion with Associated Measures in DEA[J]. Socio-Economic Planning Sciences, 2000, 34(1).

[5]崔晓东，郑玉华．基于RAM的我国财险公司效率与偿付能力关系研究[J].统计研究，2011，(3)．

[6]冯蕾．2005-2007年我国省际能源效率研究——基于DEA方法非意愿变量CRS模型的测度[J].统计研究，2009，(11)．

[7]李平，随洪光．国际技术扩散与经济增长：收敛模型[J].南开经济研究，2006，(6)．

2017-06-21

张海伟，女，山东济宁人，山东理工大学经济学院副教授，经济学博士；李平，男，浙江宁波人，山东理工大学经济与管理学部主任、教授，经济学博士。

F223

A

1672-0040(2017)05-0005-07

(责任编辑鲁守博)