不同浪向下超大型船舶载荷响应特征的模型试验研究
2017-11-06陈占阳李志鹏哈尔滨工业大学
陈占阳,李志鹏(哈尔滨工业大学
(威海) 船舶与海洋工程学院,山东 威海 264209)
不同浪向下超大型船舶载荷响应特征的模型试验研究
陈占阳,李志鹏(哈尔滨工业大学
(威海) 船舶与海洋工程学院,山东 威海 264209)
探寻超大型船振动响应随不同浪向的变化规律对预报真实海况和后期的结构评估具有重要意义。在拖曳水池对某超大型集装箱船进行了分段船模斜浪试验,详细介绍了船模设计原则和斜浪试验测试系统,并通过改变船模分段数量来探究船体弹性效应对振动响应的影响,结果表明船体自身的弹性效应对颤振影响很大,船体固有频率小,更容易出现颤振现象。研究了各浪向下的弯矩响应和砰击压力时历曲线,并对不同成分的弯矩响应和砰击压力随浪向和波长船长比的变化规律进行了分析,经分析发现,迎浪是发生高频颤振最严重的浪向,而斜浪时的最大弯矩多发生在λ/(L·cosβ)=1.0附近。相对于低频波浪弯矩,高频载荷响应对浪向的变化更加敏感。
超大型船舶;分段模型试验;波浪载荷;砰击;颤振
2015年11月,六艘当今世界最大、最新型的2.1万标准箱集装箱船在江南长兴重工基地同时开工。这预示我国对于超大型船舶的建造进入一个新的阶段。
由于这类船舶的主尺度过大,常规的计算方法无法精准地预报其载荷响应,因此,模型试验通常是研究这类船舶的重要手段之一。由于分段船模试验能够计及船体弹性振动变形对周围流场载荷的影响,因此得到广泛的应用[1-2]。近年来试验方式从拖航[3]发展到自航[4],龙骨梁从等截面梁[5]发展到变截面梁[6],分段数量也逐渐增多[7-8],试验对象更是涵盖军品和民品中的各类船型。其中,Jiao等[9]对大尺度分段船模进行海事实验,分别将测量结果与拖曳水池中的小尺度船模试验结果和数值计算结果进行了对比。
尽管相关学者对该项试验技术的掌握已日趋成熟,但由于受到试验场地和试验技术等方面的限制,目前已发表的关于分段船模试验的文献主要还是针对迎浪状态。
但众所周知,真实海况瞬息万变,海浪的方向充满很多不确定因素,因此,单纯的研究迎浪下的载荷响应,虽然能够在一定程度上为设计载荷的确定提供参考,但是无法获知斜浪中船体的载荷特性。特别是近年来不同海况下颤振响应随浪向的变化规律已越发引起人们的关注[10-12]。
因此,不同浪向下的超大型船舶载荷响应的试验研究对真实海况预报和后期结构强度评估,具有更加重要的实际意义。本文基于分段船模试验,对某13 000箱集装箱船在斜浪中的弯矩响应、砰击压力进行了测量,详细介绍了船模设计原则和斜浪试验测试系统。研究了各浪向下的弯矩响应和砰击压力时历曲线,并分析了不同成分弯矩响应和砰击压力随波长船长比、浪向和船长的变化规律。
1 分段船模试验介绍
1.1分段船模简介
传统的拖曳水池在长度上虽然能够满足船模迎浪航行要求,但无法实现不同浪向下的测量,为此本次斜浪试验是在哈尔滨工程大学(HEU)综合水池进行。该水池主尺度为50 m×30 m×10 m,XY航车X方向(水池长度方向)最高车速3 m/s,Y方向(水池宽度方向)最高车速2 m/s,航车测桥可360°转动,可以开展任意浪向(β=0°~ 360°)试验。图1为综合试验水池。

图1 哈尔滨工程大学综合试验水池Fig.1 The comprehensive test tank of HEU
模型缩尺比为1∶75,本次试验为验证船体弹性程度对高频颤振响应的影响,将船模先后分别切为二分段(在第10站即船舯分段)、六分段(在第2、4、6、8、10站分段)、十分段(在第2、4、6、8、10、12、14、16、18站分段),分段间隙约为1 cm,由变截面方钢龙骨梁连接,船壳仅作为提供浮力和将流体动力传递给龙骨梁的元件。表1为船模主尺度。图2为不同分段的模型示意图。
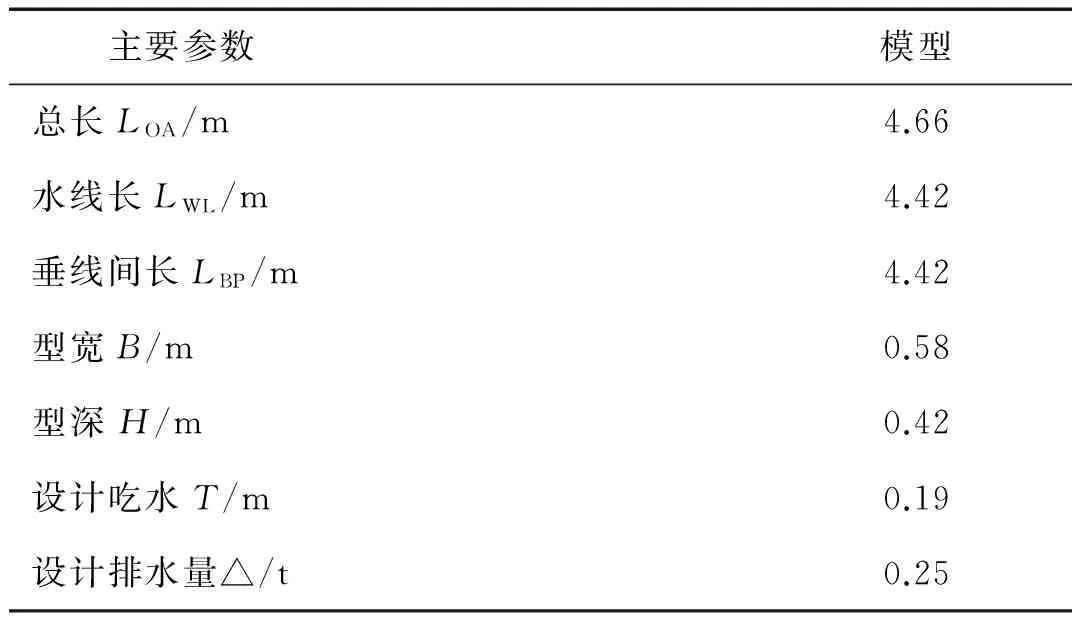
表1 模型主尺度Tab.1 Main parameters of the model
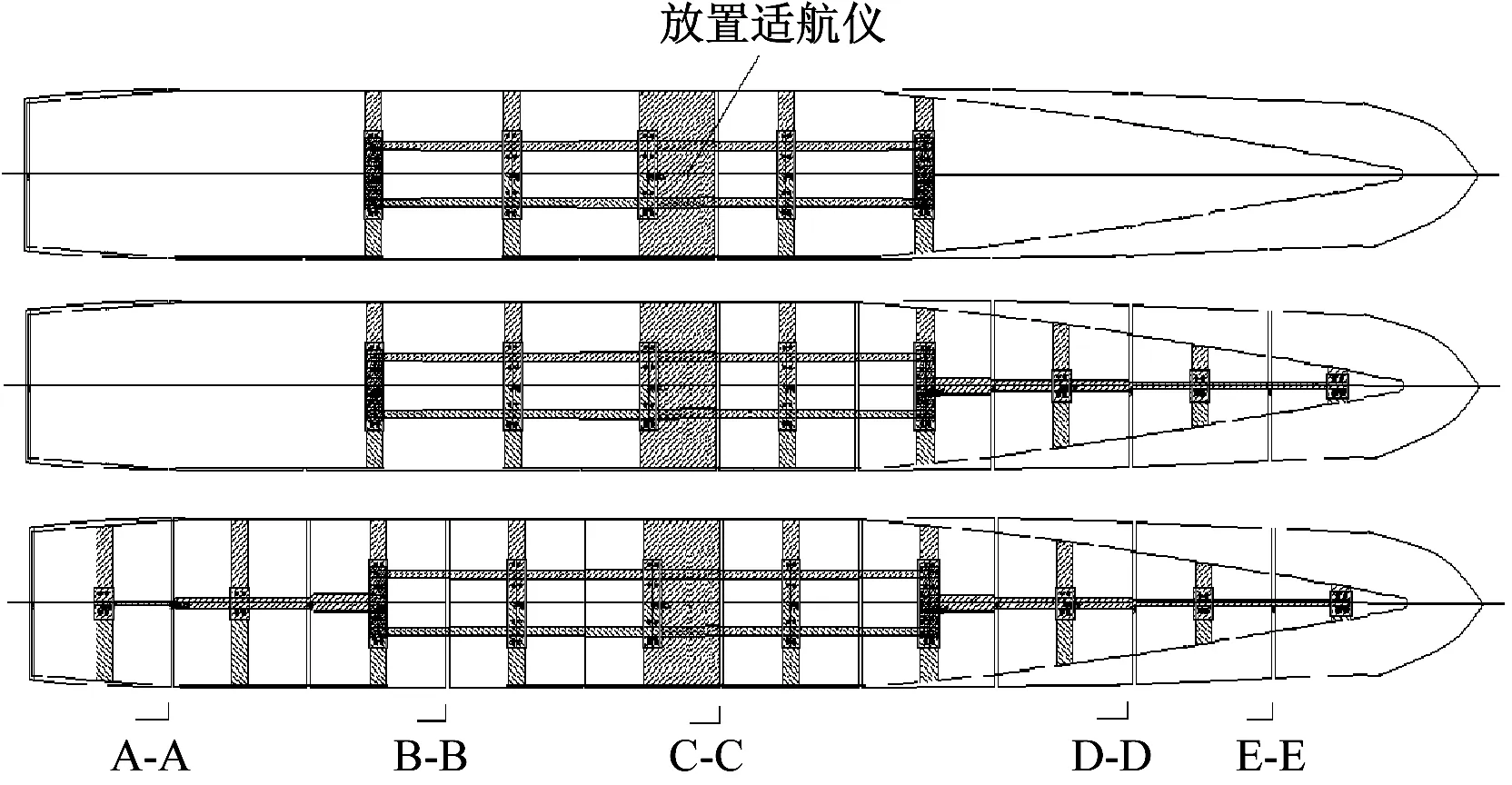
图2 不同分段的模型示意图Fig.2 The ship model with different segments
研究船体的振动响应,龙骨梁的设计是关键。首先分别基于迁移矩阵法(Transfer Matrix Method,TMM)和有限元法(Finite Element Method,FEM),对实船的模态进行分析,图3为基于这两种方法得到的前三阶固有振型沿船长的变化。本文是根据有限元法得到的实船首阶固有频率,确定龙骨梁的尺寸。
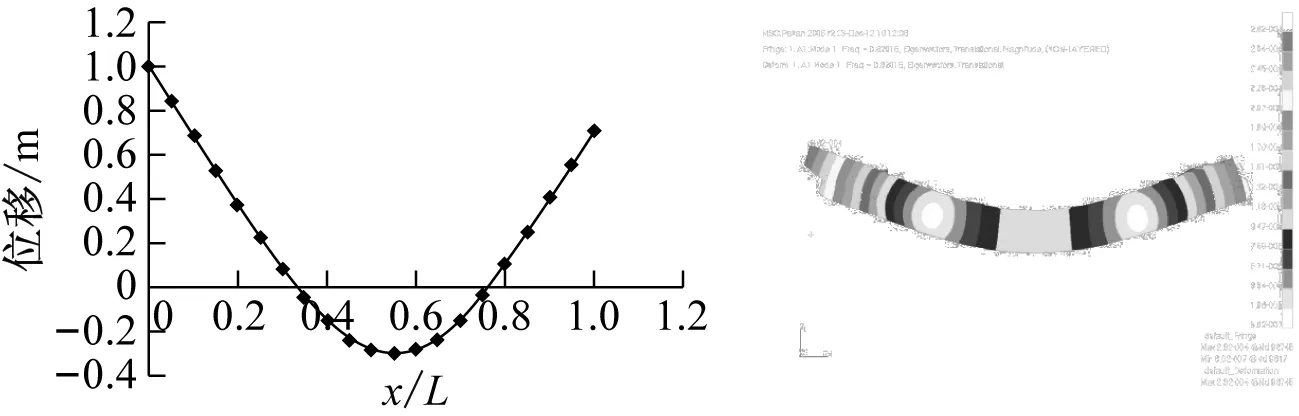
(a) 第一阶固有振型
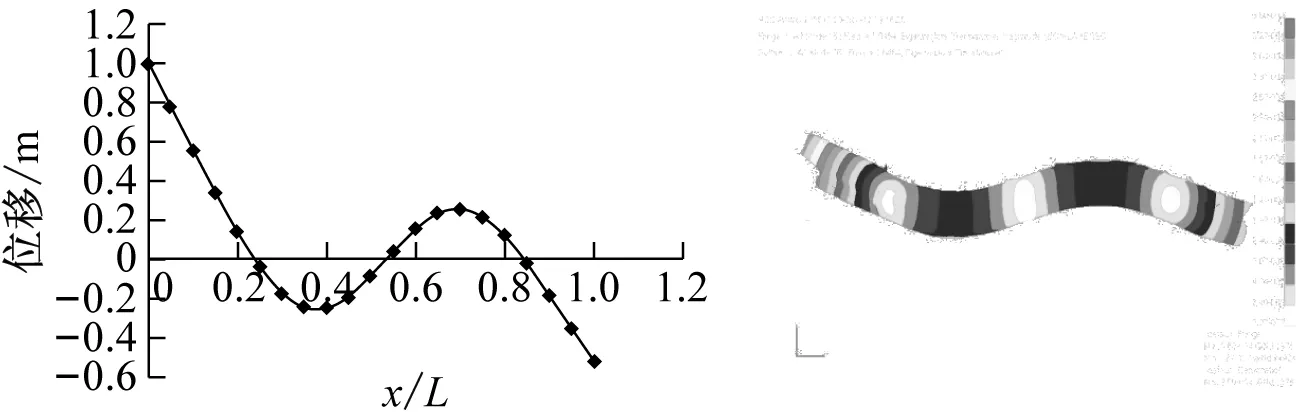
(b) 第二阶固有振型
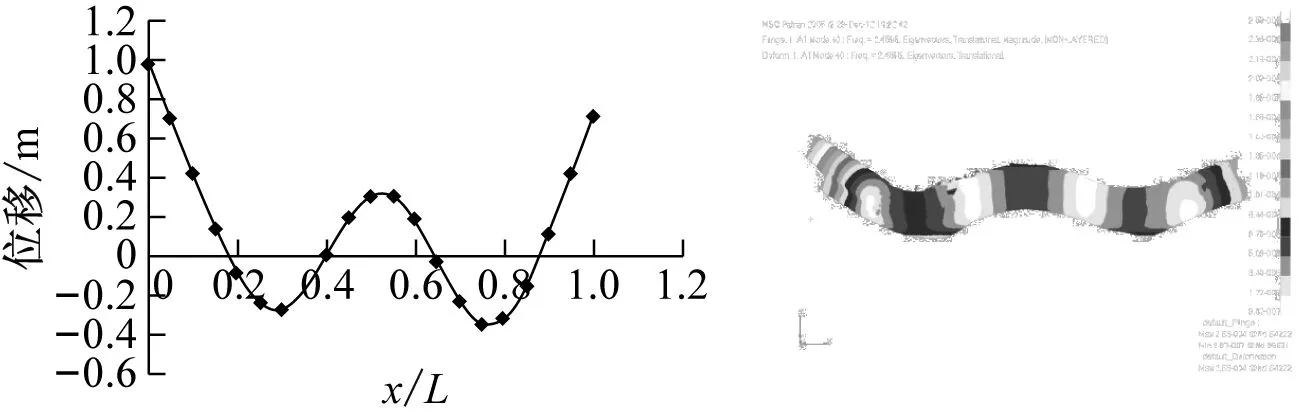
(c) 第三阶固有振型图3 基于迁移矩阵法和有限元法固有振型沿船长的变化Fig.3 The natural vibration mode along ship based on TMM and FEM
船模下水后,需先验证龙骨梁的设计是否满足要求。本文通过对船模艏部施加激振力,采集得到静水中的船舯垂向弯曲应力时历曲线,再由傅里叶变换得到船模湿模态下垂向振动固有频率。表2是不同分段的船模测量结果与理论值的比较。
表2中的理论值是基于有限元方法得到的实船湿模态固有频率,试验值是船模在水中测量值换算到实船的结果。误差1、误差2和误差3分别为二分段、六分段和十分段模型测量值与理论值的比较结果。从表中可以看出,测量结果均比理论指偏大,且随着频率阶数增高误差也随之增大,十分段的是从1.58%~10.57%;而同一模态下的固有频率,模型分段越少误差越大,仅第一阶的误差就从1.58%~43.11%。此外,模型分段数量少,不仅误差变大,同时无法测得高阶频率。分析原因是因为船模分段数量过少无法体现出高阶变形,因此建议在试验条件允许的前提下,尽可能的将船模分段增多,以获得更准确的试验结果。

表2 船模固有频率的理论值与测量值的比较Tab.2 Comparison between theoretical and Experimental natural frequency of the model
1.2测试系统简介
本次试验测控系统主要包括两大部分:拖车部分和船模部分,拖车部分以载荷信号采集器、运动信号采集器和视频采集器为测控平台;船模部分以测量对象不同,分为不同模块,将测量信号分别传输到拖车上的采集平台,图4系统组成示意图。
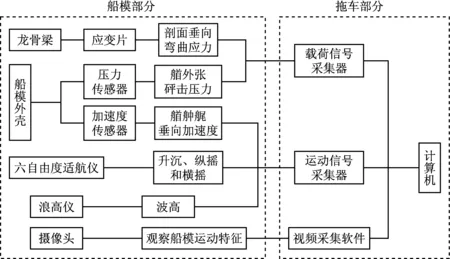
图4 试验测试系统集成示意图Fig.4 Test system integration schemes
本次试验测量工况均为规则波工况,浪向角分别为0°(迎浪)、30°、45°、60°、90°(横浪)、120°、150°。本文中对于浪向的规定见图5。
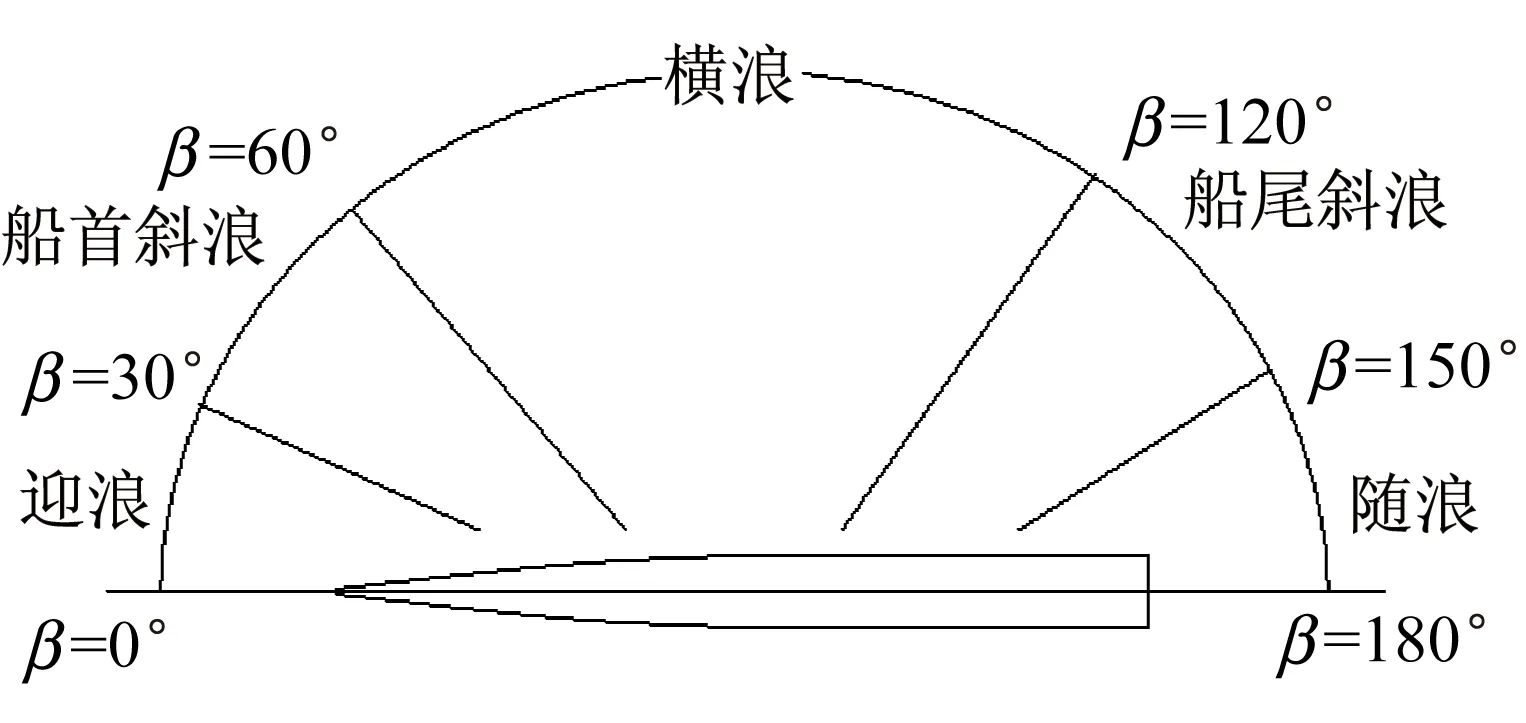
图5 浪向角的规定Fig.5 The rule of the wave direction angle
试验测量内容及所用测试仪器如下:
(1) 造波机为摇板式造波机,可以产生2D长峰规则或不规则波、3D短峰波,规则波最大波高0.4 m,不规则波有义波高最大0.3 m,造波周期0.5~4.0 s;
(2) 为了测量剖面弯曲应力,本次试验采用“全桥法”,在图2中的A~E剖面粘贴应变片;
(3) 六自由度适航仪采集升沉、纵摇、横摇等运动数据,图6是六自由度适航仪照片;
(4) 波浪由定点浪高仪测量;
(5) 分别在船模艏外飘,右舷侧布置四路压力传感器,图7是砰击压力点测试位置示意图,图8船模试验现场照片。
2 弯矩响应试验结果分析
2.1船体弹性效应对结果的影响
图9是迎浪工况(航速v=20 kn,波高h=6 m, 波长船长比λ/L=1.0)各分段状态下船舯弯矩时历曲线。通过数字滤波技术将测得的合成弯矩分离成低浪弯矩成分、高频弯矩成分。从图中可以看出,无论采用哪种分段船模,船舯弯矩都可以分为按遭遇频率变化的低频波浪弯矩和按船体梁首阶固有频率变化的高频弯矩。随着船模分段数量增多,三种模型测得的高频弯矩特性的均有明显增大,但低频波浪弯矩几乎不变。

图6 六自由度适航仪的吊装Fig.6 6-dof seaworthiness
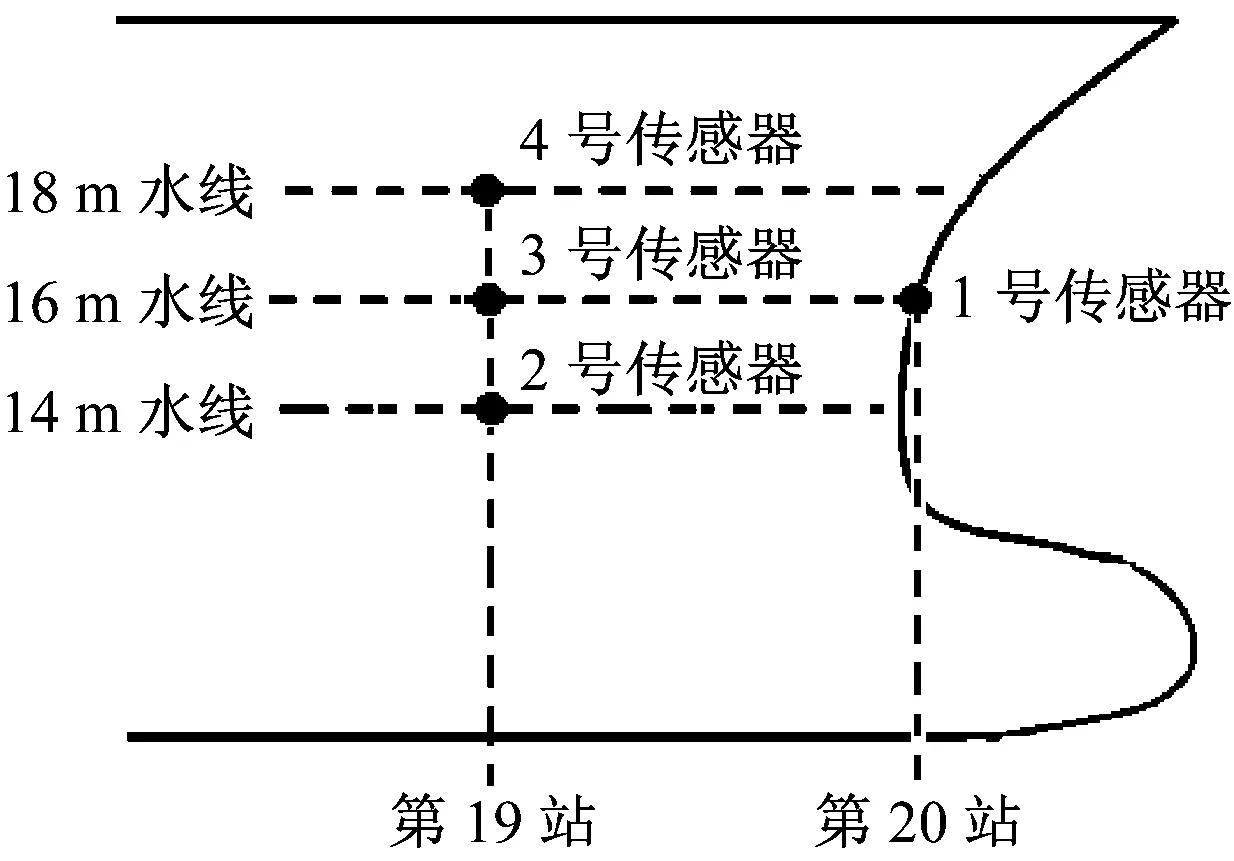
图7 砰击压力点测试位置Fig.7 Test position of slamming pressure

图8 试验现场照片Fig.8 Picture of the ship model in waves
其中图9(c)中十分段的高频弯矩表现出明显的颤振特性,即高频弯矩谷值总是发生在合成弯矩的谷值同一时刻,也就是遭遇砰击的时刻。砰击是一种瞬时冲击现象,当船体梁受到振源(砰击力) 作用的瞬间,船体梁产生的振动幅值最大,随后会在流体阻尼和结构阻尼下逐渐衰减,直至下一次砰击到来。
值得注意的是图9是在同一工况下测得的结果,却只有十分段出现了明显的颤振现象,在比较不同分段船模所受的砰击压力后发现,船模分段数量对砰击压力没有影响,说明三种模型遭遇的砰击程度是一样的,仅仅是由于船体自身的弹性效应发生了变化,就导致了不同的结果。可以断定固有频率越小的船,越容易出现颤振现象且颤振响应越大;固有频率越大的船,越不易出现颤振现象或颤振响应越小。
为更清晰地研究船体振动响应,本文接下来仅对十分段船模的测量结果进行分析。
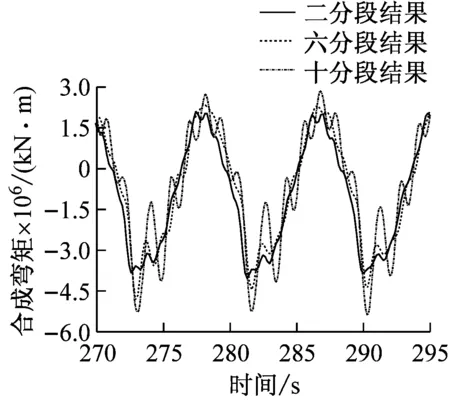
(a) 合成弯矩
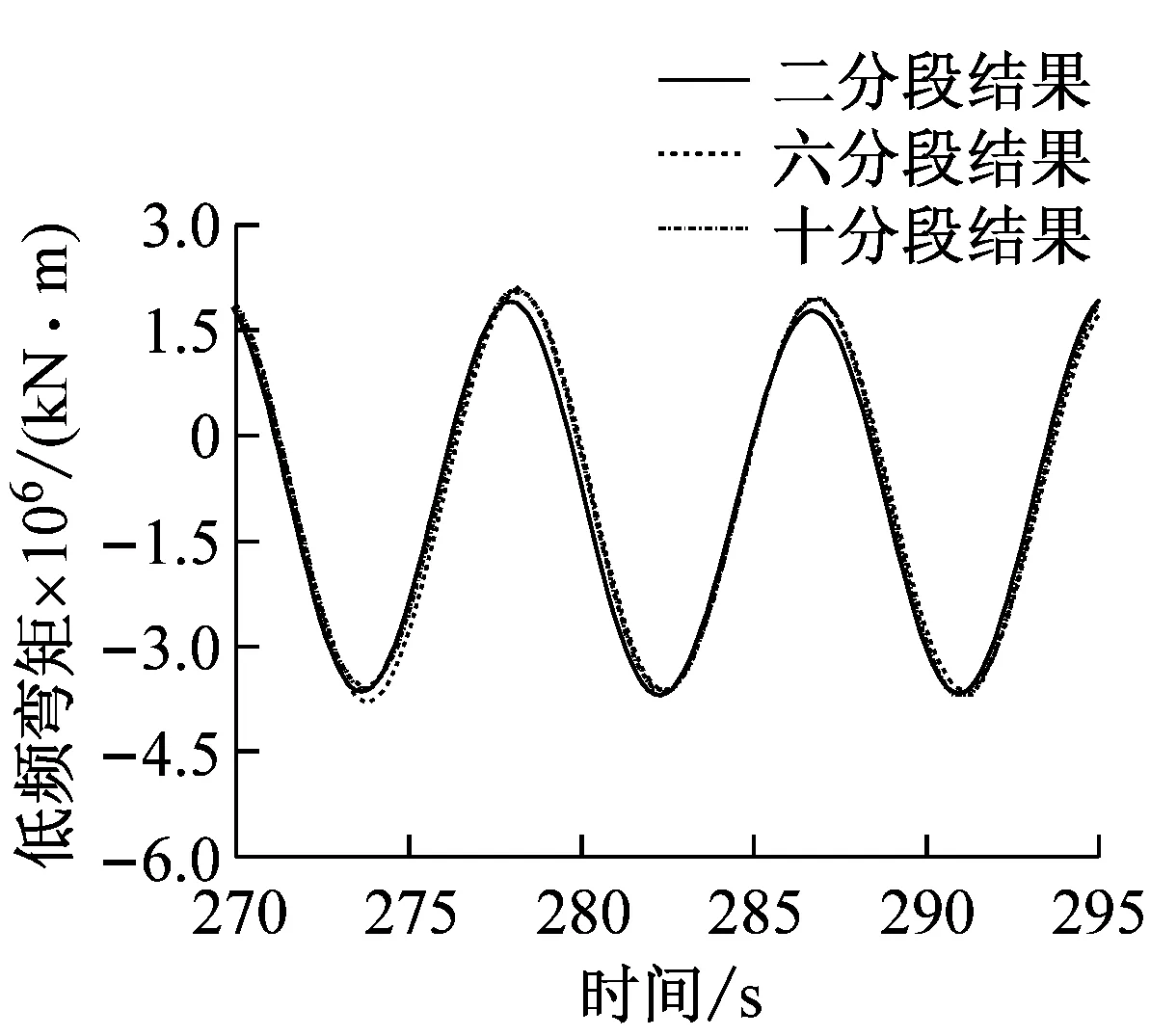
(b) 低频波浪弯矩
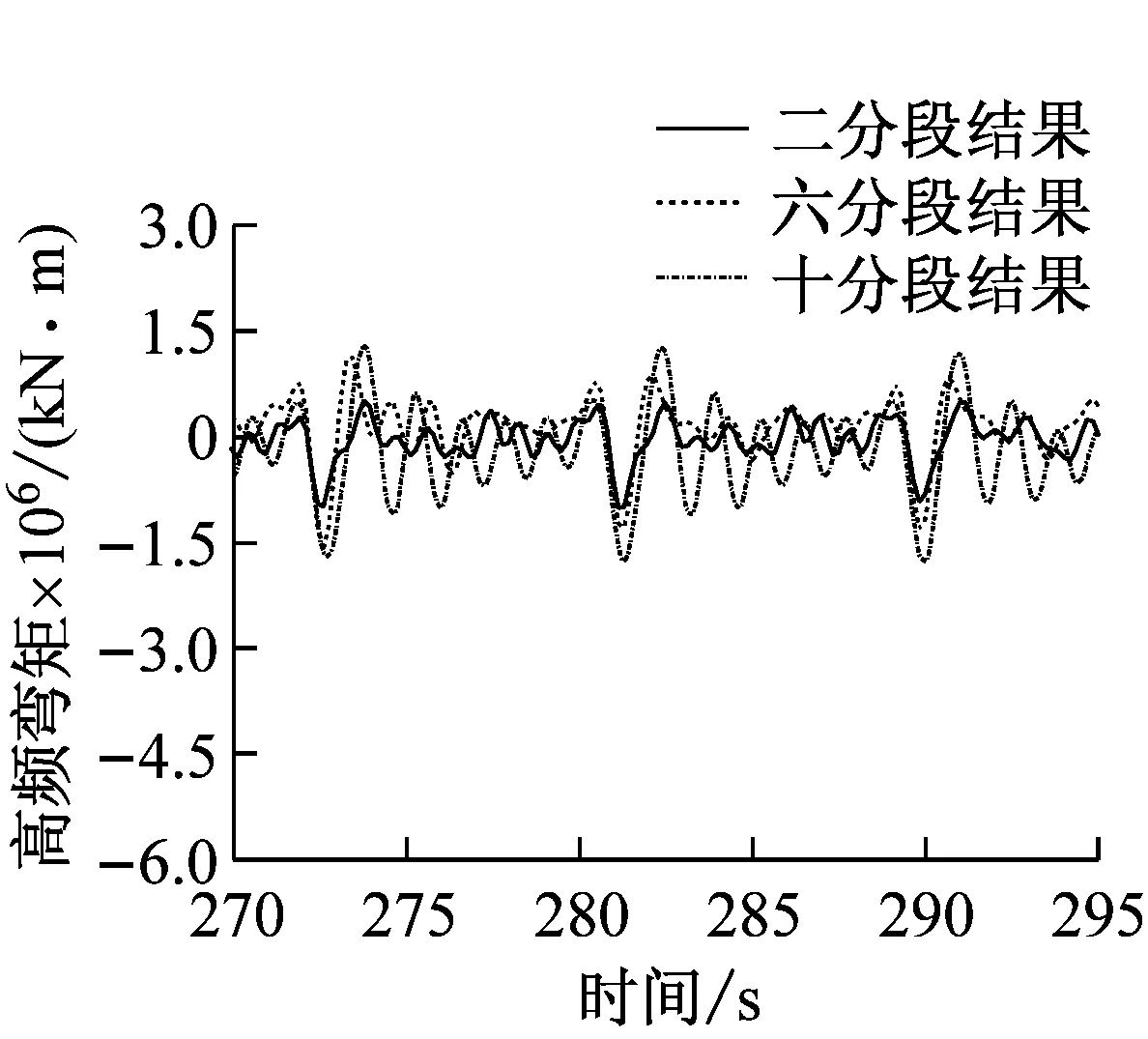
(c) 高频砰击弯矩图9 不同分段模型的船舯弯矩时历曲线比较Fig.9 The time trace of VBM with different segmented models
2.2随波长船长比的变化
图10是两个典型工况下λ/L=1.0时不同浪向角下的船舯弯矩的时历曲线。可以看出,不同浪向下的船舯弯矩时历曲线均呈周期性往复变化,但遭遇频率却不尽相同。在同一个时段内艏斜浪要比艉斜浪遭遇更多的波浪,迎浪曲线最为紧密,随着浪向角的增大,载荷响应曲线逐渐稀疏。
图中艏斜浪β=30°时的合成弯矩结果最大,但高频振动特性还是迎浪时最为显著,且随着浪向角的增大,高频振动特性越不明显。
尽管航速、波高相同的情况下,载荷响应中的高频特性受浪向的影响依然很大。这是因为随浪遭遇频率要比迎浪小,由式(1)可知,随着浪向角的增大,遭遇频率逐渐减小,距离船体固有频率频带(f1st=6.41 Hz→f2nd=16.02 Hz→f3rd=29.40 Hz) 越来越远。由此可见,在航速、波高不变的情况下,固有频率与遭遇频率的“距离”是影响高频振动响应的直接原因。
(1)
此外,随着海况增大,迎浪和艏斜浪下的高频响应成分明显增加,而艉斜浪时的变化很小,横浪下几乎不变。
图11是两个典型工况下船舯弯矩全幅值无因次化结果随浪向和波长船长比的变化。弯矩的无因次化方法为M/ρgζL2B,式中ρ为水的密度,g为重力加速度,ζ为波幅,L为水线长,B为型宽。
从图中可以看出,对于不同波长船长比而言,船舯垂向弯矩随浪向的变化规律基本一致,当β=0°~90°时,测量结果随着浪向角的递增而减小;当β=90°~150°时,结果随着浪向角的递增而增大。当β=90°时,测量结果达到最小。
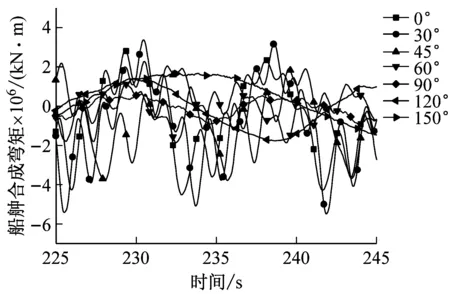
(a) v=20 kn,h=6 m

(b) v=9 kn,h=14 m图10 不同浪向船舯弯矩时历曲线Fig.10 The time trace of VBM under different wave directions
而对于不同浪向下,船舯垂向弯矩随波长船长比的变化规律有所不同。当β=0°时,最大值发生在λ/L=1.0;当β=30°和150°时,最大值发生在λ/L=0.9;当β=45°时,最大值发生在λ/L=0.7;当β=60°和120°时,最大值发生在λ/L=0.6。斜浪状态下的这一变化规律与迎浪工况明显不同,经分析后发现斜浪中垂向弯矩测试结果的最大值是在λ/(L·cosβ)=1.0附近。
2.3沿船长变化
从图10的时历曲线中看出浪向对高频成分也有显著的影响,为分析船体不同剖面各成分弯矩随浪向的变化,将v=9 kn,h=14 m,λ/L=1.0时不同浪向下各成分载荷响应无因次化结果沿船长变化进行统计,见表3。表中M1~M5分别为图2中剖面A~E的弯矩响应。MHF表示高频振动响应所占的比重,MLF表示高频波浪弯矩响应所占的比重。
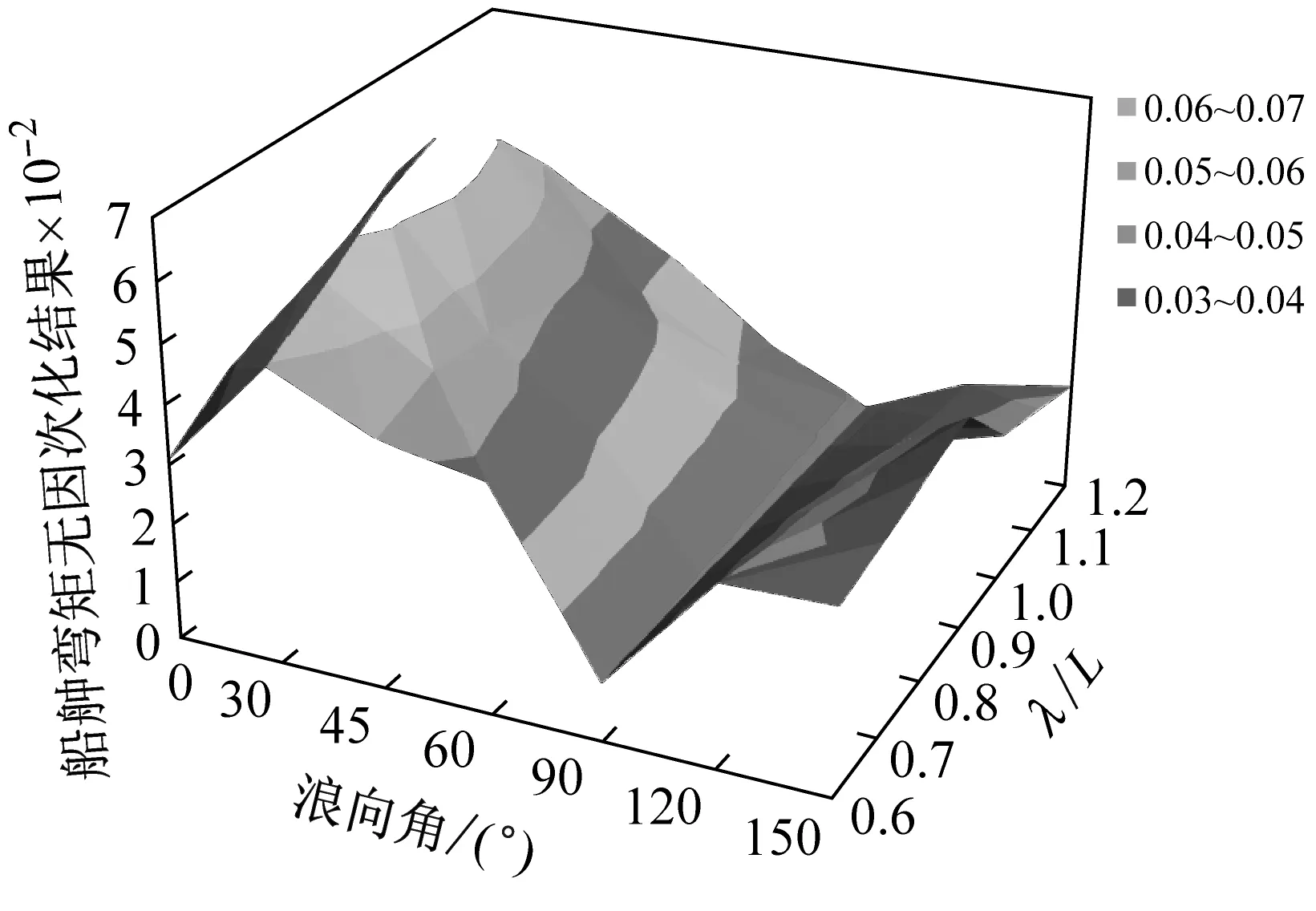
(a) v=20 kn,h=6 m
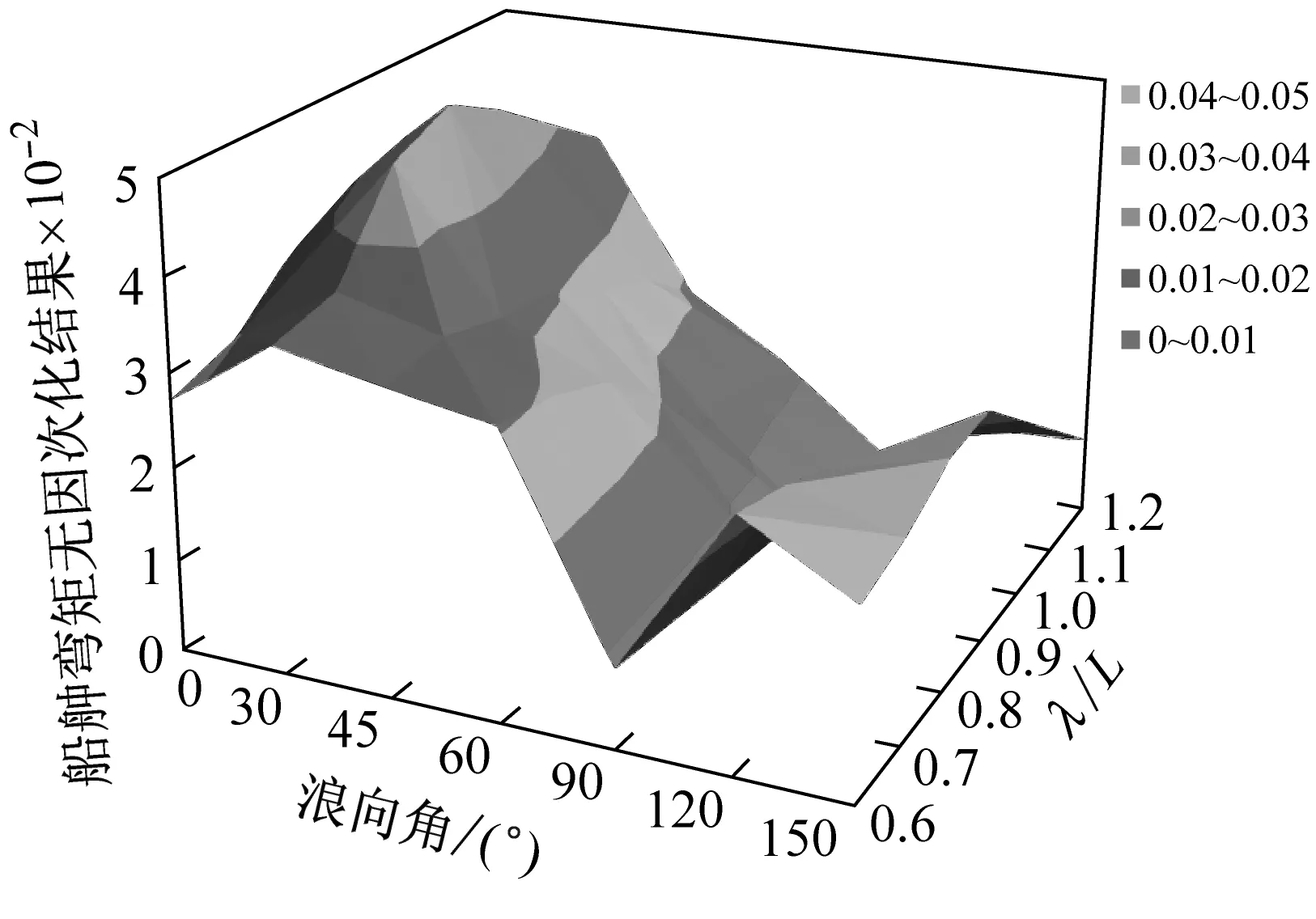
(b) v=9 kn,h=14 m图11 船舯弯矩随浪向和波长船长比的变化趋势图Fig.11 The change of VBM with the wave direction and ratio of wave length to ship length
从图中可以看出,船舯处的高频砰击弯矩始终为最大的。然后逐渐向两端递减。由于测量的是垂向弯矩,越是接近横浪,高频弯矩就越小。同样的波高和航速下,迎浪船舯高频砰击弯矩成分比例达58.73%,而横浪时仅为17.17%,其他的剖面也呈现出这一趋势。当浪向角超过90°时,各剖面的高频弯矩成分均呈上升趋势。由此可见浪向对高频成分影响不容忽视。
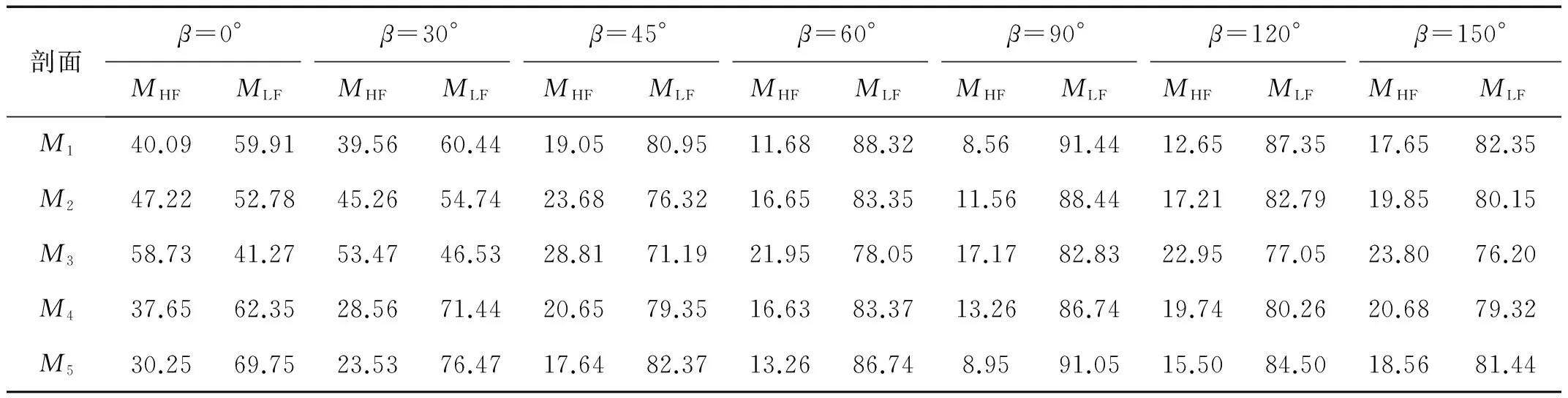
表3 不同浪向下各成分载荷响应沿船长变化统计Tab.3 Statisics of longitudinal distribution of ship bending moments under different wave directions %
3 砰击压力试验结果分析
图12~图15是v=20 kn,h=6 m,λ/L=1.0的在β=0°、β=30°和β=45°时各点砰击压力时历曲线。迎浪时,压力值最大的点是1号传感器,舷侧测量点(2号~4号传感器)的砰击特性不如艏外飘处的明显,测得的砰击压力峰值没有出现“尖点”。
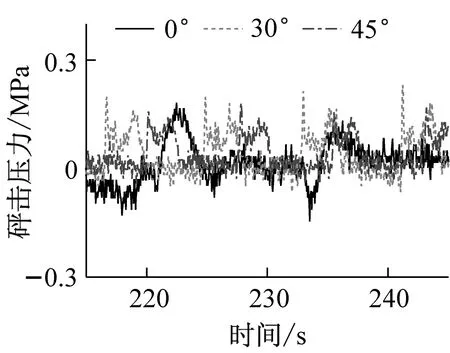
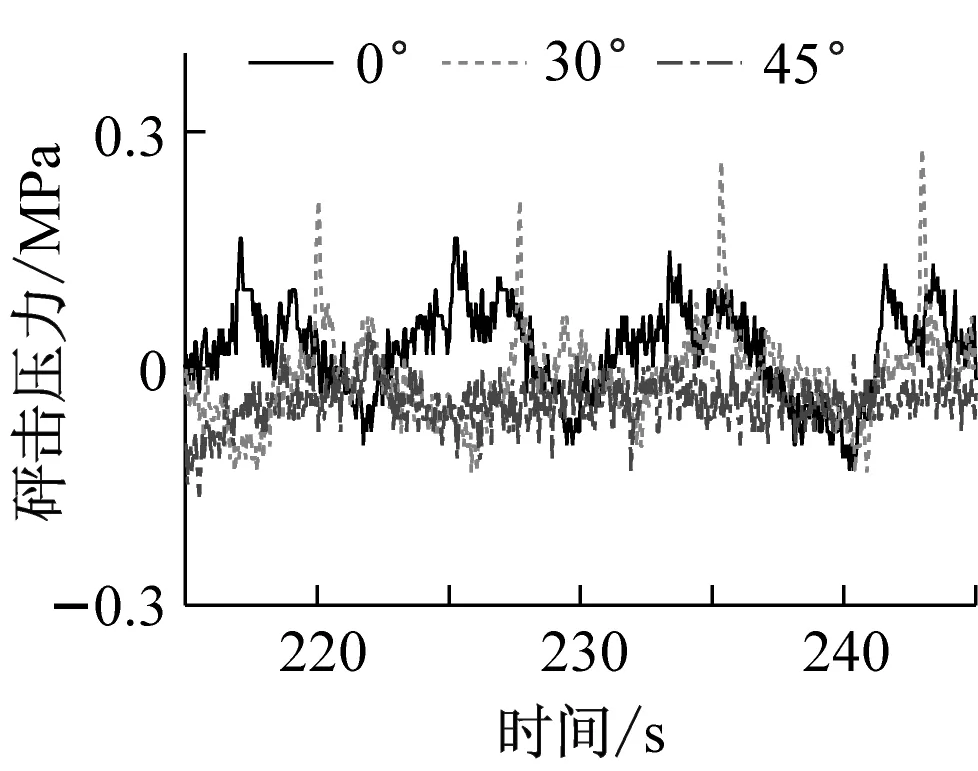
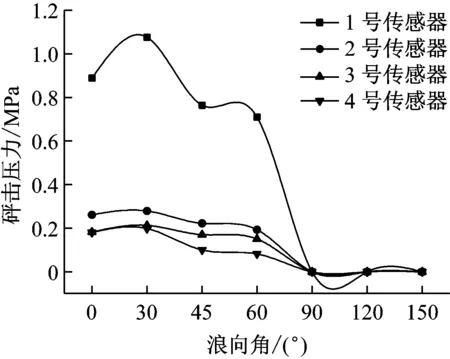
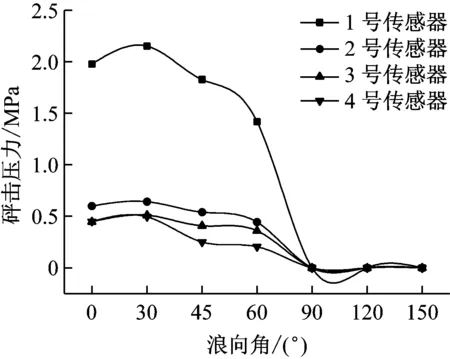
对于舷侧砰击压力,有P4 图12 1号传感器砰击压力时历曲线 图13 2号传感器砰击压力时历曲线Fig.13 Time trace of the slamming pressure of No 2 图14 3号传感器砰击压力时历曲线Fig.14 Time trace of the slamming pressure of No 3 图15 4号传感器砰击压力时历曲线Fig.15 Time trace of the slamming pressure of No 4 图16 砰击压力随浪向变化(v=20 kn,h=6 m)Fig.16 The change of slamming pressure with the wave direction (v=20 kn,h=6 m) 图17 砰击压力随浪向变化(v=9 kn,h=14 m)Fig.17 The change of slamming pressure with the wave direction (v=9 kn,h=14 m) 从图中可以看出,1号传感器的砰击压力始终最大,且发生最大的砰击压力的浪向为β=30°的时候,这与弯矩结果相同。但随着浪向角的增大,舷侧的压力虽然都呈减小的趋势,但与1号测量结果的差距却越来越小,斜浪时要注意舷侧的外张砰击压力。 此外,本次试验中横浪和随浪状态(β=90°)各点均没有采集到砰击压力值。 本文基于分段船模斜浪试验分析了不同浪向下船体载荷响应特性,较为详尽的介绍了分段船模的设计原则和斜浪测量方法,通过对试验结果的分析得到以下结论: (1) 分段试验的船模设计关键是首阶固有频率是否满足要求,通过检验发现,船模分段越少误差越大,且无法测得高阶的固有频率,该特性同样也反映在载荷响应测量当中。因此建议在试验条件允许的情况下,增多船模分段,以获得更精准的试验结果。 (2) 船体自身的弹性效应对颤振影响很大,越“软”的船(固有频率越小),越容易出现颤振现象且颤振响应越大;越“硬”的船(固有频率越大),越不易出现颤振现象或颤振响应越小。 (3) 本次试验中发生颤振最严重的是迎浪,发生最大弯矩的剖面为船舯剖面。斜浪时的最大弯矩多发生在λ/(L·cosβ)=1.0附近。相对于低频波浪弯矩,高频载荷响应对浪向的变化更加敏感,船舯高频成分占总弯矩的58.73%,高频成分最小的是横浪,仅为17.17%。 (4) 即使是在斜浪状态,艏外飘处正中位置的砰击压力也是最大的,舷侧的砰击特性不够明显,但随着浪向角的增大,与艏外飘测量结果差距减小。 本文中仅就不同浪向下的载荷响应进行了测量分析,而对于不同浪向下颤振响应对船体极限强度的影响将会在以后的工作中进行研究。 [2] LEE K H, CHO S, KIM K T, et al. Hydroelastic analysis of floating structures with liquid tanks and comparison with experimental tests [J]. Applied Ocean Research, 2015, 52: 167-187. [3] LAVROFF J, DAVIS M R, HOLLOWAY D S, et al. The whipping vibratory response of a hydroelastic segmented catamaran model[C]∥Ninth International Conference on Fast Sea Transportation. Shanghai: FAST, 2007. [4] JIAO J L, REN H L, ADENYA C A. Experimental and numerical analysis of hull girder vibrations and bow impact of a large ship sailing in waves[J]. Shock and Vibration, 2015(3): 1-10. [5] ROUSSET J M, FERRANT P, ALESSANDRINI B. Experiments on a segmented ship model in directional irregular waves[C]//The 25th the International Workshop on Water Waves and Floating Bodies.Harbin:[s.n.],2010. [6] CHEN Zhanyang,REN Huilong,LI Hui,et al. Experimental and numerical analysis of bow slamming and whipping in different sea states [J].Journal of Ship Mechanics, 2012, 16(3):246-253. [7] DRUMMENA I, WU M K, MOANL T. Experimental and numerical study of containership responses in severe head seas [J]. Marine Structures, 2009, 22(2):172-193. [8] SENJANOVIC I, MALENICA S, TOMASEVIC S. Hydroelasticity of large container ships [J]. Marine Structures, 2009,22(2):287-314. [9] JIAO J L, REN H L, SUN S Z, et al. Investigation of a ship’s hydroelasticity and seakeeping performance by means of large-scale segmented self-propelling model sea trial [J]. Journal of Zhejiang University-Science A (Applied Physics & Engineering), 2015, 16(5): 387-404. [10] 翟钢军,程勇,马哲. 超大型浮式储油船的水弹性响应预报[J]. 振动与冲击,2014,33(1):141-148. ZHAI Gangjun, CHENG Yong, MA Zhe. Hydroelastic response prediction of very large floating oil storage vessel [J]. Journal of Vibration and Shock, 2014, 33(1):141-148. [11] KIM J H, KIM Y, YUCK R H. Comparison of slamming and whipping loads by fully coupled hydroelastic analysis and experimental measurement[J]. Journal of Fluids and Structures, 2014,52: 145-165. [12] 陈占阳,任慧龙,李辉. 水弹性理论与分段模型试验在船 体振动响应分析中的应用[J]. 振动与冲击,2012,31(24):119-124. CHEN Zhanyang,REN Huilong,LI Hui. Application of hydroelasticity theory and segmented model test in hull vibration response analysis [J]. Journal of Vibration and Shock, 2012, 31(24):119-124. Experimentalmodelanalysisofloadresponsesofultra-largevesselsunderdifferentdirectionwaves CHEN Zhanyang, LI Zhipeng (College of Naval Architecture and Ocean Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China) It is of great importance to evaluate the vibration responses of ultra-large vessels under different wave directions. The segmented ship model test of an ultra-large container ship under oblique wave was carried out in a towing tank. The design principle of the segmented ship model and oblique wave test system were introduced detailedly. Changing the number of segments of the model, the influence of the hull elasticity on vibration responses was studied. The experimental results show that the elastic effect of hull has great influence on the whipping, and the lower the natural frequency of hull is, the earlier the whipping phenomenon occurs. The time histories of bending moments and slamming pressure under different direction waves were discussed, and the responses of different bending moment components and the slamming pressure under different direction waves and with different ratios of wave length to ship length were analyzed.It is shown that the most serious whipping occurs under head waves, and the maximum bending moment under oblique wave is near byλ/(L·cosβ)=1.0. Compared with low frequency wave moments, high frequency load responses are more sensitive to the change of wave direction. ultra-large vessel; segmented model experiment; wave load; slamming; whipping U661.44 A 10.13465/j.cnki.jvs.2017.19.017 2015年国际自然科学基金(51509062);2014年山东省自然科学基金(ZR2014EEP024);中央高校基本科研业务费专项资金资助(HIT.NSRIF.201727);威海市科技发展计划项目(2015DXGJMS009) 2016-04-08 修改稿收到日期:2016-07-27 陈占阳 男,博士,讲师,1984年生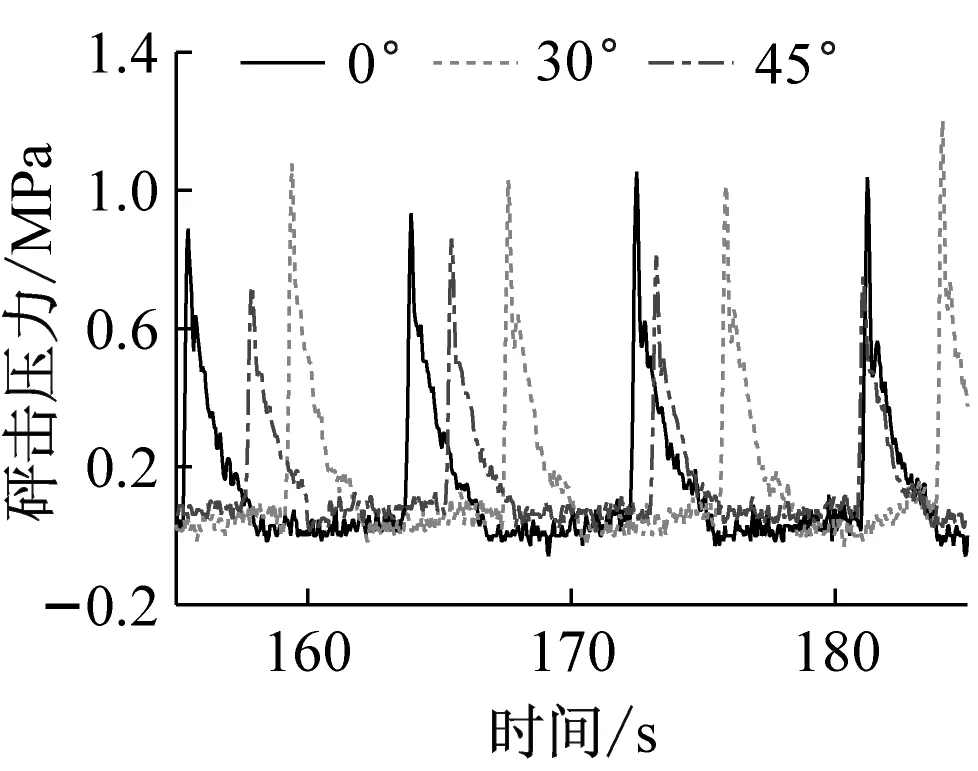
Fig.12 Time trace of the slamming pressure of No 1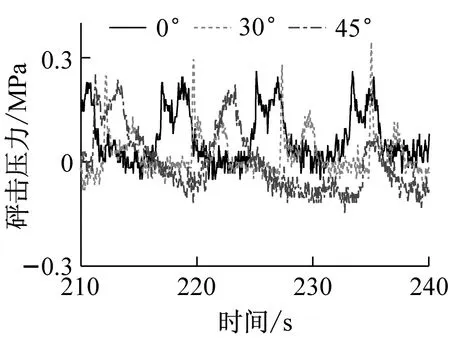
4 结 论
