新型密封偏心自适应调节方法与减振实验研究

李 宽，何立东，涂 霆

(北京化工大学 化工安全教育部工程研究中心，北京 100029)

新型密封偏心自适应调节方法与减振实验研究

李 宽，何立东，涂 霆

(北京化工大学 化工安全教育部工程研究中心，北京 100029)

针对转子偏心引起的密封流体激振问题，设计了一种新型偏心自适应调节密封结构。该结构可自适应地减小转子偏心量，抑制密封流体激振。对其抑振机理进行探究，得出当偏心自调结构的固有频率和转子密封系统的激励频率一致时，其抑振效果最好；随着两者差值增大，其抑振效果变弱。以水作为密封介质，测量了不同弹簧刚度下偏心自调结构的固有频率，并改变转子转频，对其抑振规律进行实验研究。结果表明该结构固有频率随弹簧刚度增大而增大，但与激励频率差别较大，振动降幅只在10%～20%。将偏心自调结构浸于水，测量其固有频率，对其抑振规律进行实验研究。结果表明浸在水中时该结构固有频率值依然随弹簧刚度增大而增大，但比在空气中时减小了约40%，更加接近激励频率，抑制效果显著，振动降幅最大可达41.27%。

非接触密封；密封流体激振；偏心自适应调节；固有频率

密封流体激振[1]是导致高速旋转机械转子剧烈振动的重要原因之一，目前针对密封激振的控制方法研究，有被动控制和主动控制两大类。被动控制采用不同形式的阻尼密封、阻旋栅(Swirl Brakes)等结构来抑制激振。主动控制则运用反旋流技术、可控吸气技术和合成射流等技术控制激振。

阻尼密封是用粗糙静子面来消耗流体周向流动速度，包括蜂窝密封、孔型密封、袋型密封、锯齿密封、三角形密封、菱窝密封和刷式密封等。其中蜂窝密封和孔型密封的理论相对成熟，在实际中都有很大的运用与发展，其余几种阻尼密封在制造方面和使用性能等方面都存在一些不成熟的地方。1985年，美国航天飞机主引擎的高压液氧涡轮泵中，通过把阶梯状迷宫密封(齿在转子上)更换成为恒定间隙的光滑转子面蜂窝密封后消除了转子的同步振动和亚同步振动问题[2]。孔型密封的泄漏量曾被Childs等[3]证明是光滑密封的1/3，且交叉刚度系数减小了20%。国内外对孔型密动力特性系数及密封性能有较多理论和实验研究。Childs等设计了一种孔深沿轴向变化的孔型密封，确定了最佳的孔深变化规律，发现这种孔深变化的孔型密封有效阻尼系数比传统孔型密封大1.6倍以上，且泄漏量小于传统孔型密封。Nielsen等[4]采用基于CFD(Computational Fluid Dynamics)的非定常扰动模型分析和计算了蜂窝密封和孔型密封在转子轴心随时间扰动情况下的激振力，并得到了不同激励频率下两种密封的动力特性系数，发现偏心率达到0.9时，转子稳定性大幅下降，实验和理论结果吻合较好，证明了该模型预测孔型密封动力特性系数的准确性。 阻旋栅是一种在密封入口沿周向布置的栅板，其结构简单，可以改变密封入口流体方向，有效降低入口预旋，减小密封流体激振力。阻旋栅多用于高压离心压缩机和航空发动机级间密封和口环密封。Da Soghe等[5]应用CFD方法建立阻旋栅密封静力特性求解模型，研究了单一形式阻旋栅对迷宫密封泄漏量与流场特性的影响。Childs等[6]研究了反向阻旋栅(Negative-Swirl Brake)的有效阻尼系数和交叉刚度系数，发现反向阻旋栅与普通阻旋栅相比有更高的有效阻尼系数，并且交叉刚度系数变为负数，能大大提升转子稳定性，且可以应用于多种密封场合。

反旋流技术是在迷宫密封腔内导入一股与转子旋转方向相反的汽流，抵消密封腔气流的周向运动，破坏激振漩涡，达到抑制振动的目的。反旋流技术在上世纪90年代初已有应用，吕成龙等[7]通过实验研究发现合适的喷射流量和喷射位置才能对密封流体激振起到抑制作用，从而降低转轴的振动；且喷射流量与转子不平衡质量的大小有着密切关系，一般情况下，不平衡质量越大，喷射流量需越大；由于单喷嘴的喷射流量限制，双喷嘴减振效果要优于单喷嘴。尹德志[8]研究的一种吸气减振技术，与反旋流的喷入办法相反，通过在密封间隙周向高压的位置吸出流体，以减小压力不平衡问题。合成射流技术机理是利用振动膜的振动改变腔体压强，带动主流场流体进出孔或狭缝，产生进入流场的涡对或涡环，起到流动控制作用[9]，但它设计复杂，在密封流体激振控制方面的应用研究较少。

综上所述，现如今主要是通过增加静子面的粗糙度、喷射相反方向的流体等减小流体周向速度的方法来抑制密封流体激振，对导致激振的另一原因——转子偏心并未改善，密封中的转子依然处于偏心状态，仍然会产生流体激振力。另外，现今密封减振领域对于调节和控制密封腔内转子偏心的技术研究也较少，基于此背景，本论文设计了一种新型偏心自适应调节密封结构，以下简称偏心自调结构。通过实验的方法，研究了未安装与安装偏心自调结构时转子密封系统的振动情况，分析了本结构对密封流体激振的抑制机理。

1 新型偏心自适应调节密封结构设计

所设计的偏心自调结构主要由密封内环、弹簧和密封外环组成。密封内环是一个不锈钢薄壁圆筒，其内侧与转子形成密封间隙，外侧套有一个周向带孔圆环，用于连接弹簧一端；弹簧周向均布四个，其另一端与密封外环相连；密封外环为静子，其周向也打有孔，每隔90°孔内旋有一个尾部带孔的螺栓，用于连接弹簧的另一端。可通过旋出螺栓来拉紧弹簧，使得传统结构中的密封外环静子中增加了一个可动的密封内环，构成了偏心自调结构。其结构如图1所示。

图1 偏心自调密封结构Fig.1 The eccentricity self-adjusting seal structure

偏心自调结构的设计旨在解决工业非接触密封中由转子偏心引起的强烈流体激振问题，主要特点是在原密封静子内增加一个可动的密封内环(不改变原有密封间隙)，通过周向偶数个弹簧连接在密封外环静子上，使其能根据转子的振动状态自适应地调整密封内环的径向位置，一方面减小转子偏心量，改善密封间隙周向压力的不均匀分布情况，减小激振力；另一方面，转子的振动可通过流体传递，变为密封内环的振动，把转子的振动能量转移给密封内环，提高转子稳定性。

2 偏心自调结构减振机理探究

2.1偏心自适应调节

一般认为，传统密封结构产生密封流体激振的因素主要有两方面，即转子的偏心和密封腔流体的周向流动。由于轴系因制造、安装、偏磨或旋转产生涡动运动等因素而偏心，导致密封间隙周向不均匀，进而导致周向压力分布不均，形成高压区和低压区，如图2(a)所示，图中ω为转子转频。流体在密封腔中的螺旋形流动又使周向压力分布的变化与密封间隙变化不完全对应，最高压力区滞后密封腔最小间隙一定角度，形成激振力。当激振力超过一定值时，就会使转子强烈振动。

基于以上的密封流体激振机理，本文在传统密封结构的密封静子中增加一个密封内环，用周向四个弹簧将密封内环连接到密封外环静子上，如图2(b)所示。当转子偏心时，密封腔内的不均匀压力迫使密封内环向转子偏心方向移动，使临近高压区的小间隙增大，临近低压区的大间隙减小，周向间隙和周向压力分布趋于均匀，实现对转子偏心量的自适应调节，抑制密封流体激振，提高转子密封系统的稳定性。一般情况下，减小偏心量则可以相应地减少泄漏量[10]，故偏心自调结构在减小转子偏心量的同时也有助于密封性能的提升。

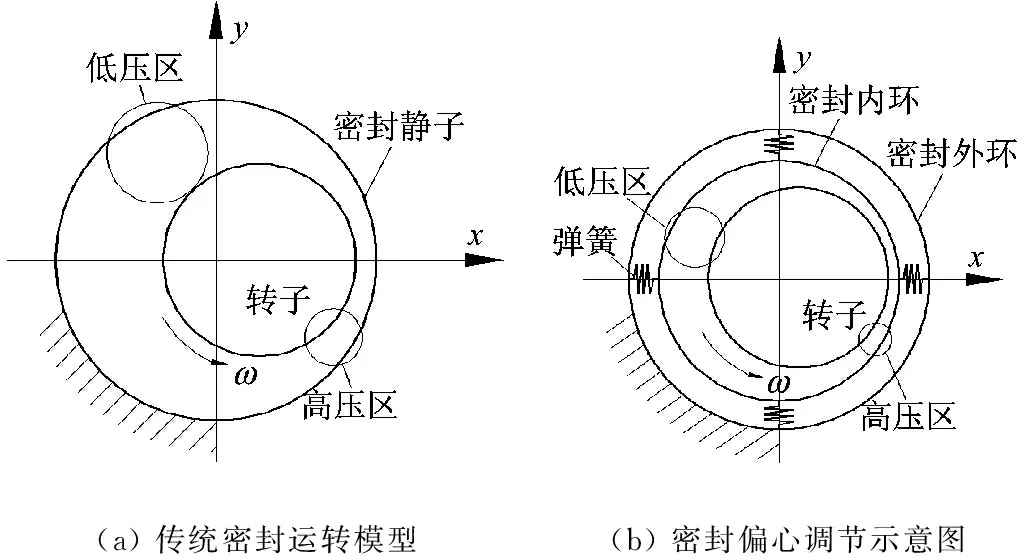
(a)传统密封运转模型(b)密封偏心调节示意图

需要注意的是，偏心自调结构中密封内环的运动直接受到其外侧弹簧的影响，从而影响偏心自调结构的减振效果。故需确定不同弹簧刚度下偏心自调结构的减振规律，寻求合适的弹簧刚度。

2.2偏心自调结构动力学分析

为确定弹簧刚度对偏心自调结构减振效果的影响规律，本文进一步建立了如图3所示的偏心自调结构动力学模型，从动力学角度分析由转子至密封内环的振动传递率与弹簧刚度的关系。图3中：m1为转子质量，m2为密封内环质量；k1为密封腔内流体的刚度，k为螺旋弹簧的刚度；x1为转子位移，x2为密封内环位移；F1为激励力。

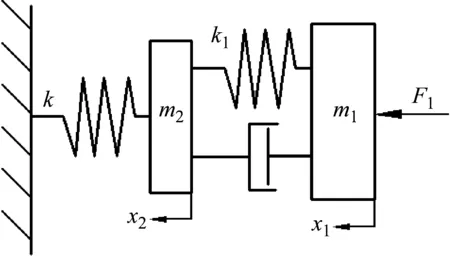
图3 偏心自调结构动力学模型Fig.3 Eccentricity self-adjusting structure dynamic model

得到偏心自调结构的运动微分方程

(1)

设激振力F1的激励频率为ω，将F1简化为简谐激励力|F1|ejω，激励力使转子产生的位移为x1=X1ejω，密封内环产生的位移为x2=X2ejω，在不考虑阻尼的情况下，振动传递系数为[11]

(2)

式中：ω1为转子的固有频率;ω2为偏心自调结构的固有频率。由于ω1固定不变，故在此只讨论ω2与振动传递系数Tf的关系。由式(2)可知，当ω2与激励频率ω越接近，即1-(ω/ω2)2越小，振动传递系数Tf越大，振动由转子传递至密封内环的效果越好，转子越稳定。反之，若1-(ω/ω2)2越大，振动传递系数Tf越小，则越不利于转子稳定。

本模型中，偏心自调结构的固有频率为

(3)

由式(3)可知，ω2的大小可通过改变弹簧刚度k来调节，使其与激励力频率ω接近，增大振动传递系数Tf，以减小转子振动。所以，为了使密封偏心自调结构的减振效果达到最好，需根据具体工况和具体结构确定合适的弹簧刚度k。

3 偏心自调结构抑制流体激振实验研究

3.1实验台参数

为验证理论分析，本文搭建了密封实验台，设计了五种弹簧刚度为1.08 N/mm、2.0 N/mm、3.2 N/mm、6.12 N/mm和9.03 N/mm的偏心自调结构，以水为密封介质，开展了本结构对转子密封系统的抑振规律实验研究。实验台主要由电机、不锈钢薄壁圆筒、盛水容器、偏心自调结构、电涡流传感器、LC8008振动信号分析仪、计算机等组成，如图4(a)所示。实验转子和密封内环分别是一个外径为150 mm和一个内径为160 mm的不锈钢薄壁圆筒，二者之间构成密封腔。其中密封内环是偏心自调结构的一部分，偏心自调结构与盛水容器固定，转子与电机主轴通过螺纹连接。当密封内环与转子同心时，两个薄壁圆筒壁面之间距离即密封间隙为5 mm，密封长度为70 mm。实验台实物见图4(b)。

为模拟转子偏心造成周向压力分布不均以致激振的工况，将图4中转子的右侧设定为最小间隙，用塞尺测量，使转子偏心量为2 mm，最小密封间隙为3 mm。电机架上安装有位移传感器，用于测量转子密封系统的振动位移。电涡流传感器测出转子振幅后通过LC8008信号分析仪进行信号转换，由计算机显示振动数据。所用位移传感器为LC-18电涡流位移传感器，其分辨率为1 μm，灵敏度为8 mV/μm，线性电压范围为0 V～24 V, 有效测量范围为0 μm～1 500 μm。

(a) 实验台示意图

(b) 实验台实物图图4 偏心自调密封结构试验台Fig.4 Eccentricity self-adjusting seal structure test rig

3.2偏心自调结构减振规律实验研究

根据理论分析，偏心自调结构的抑振效果与频率比ω/ω2的值是否接近1有关，故实验测试了弹簧刚度值k为1.08 N/mm、2.0 N/mm、3.2 N/mm、6.12 N/mm和9.03 N/mm时偏心自调结构的固有频率ω2。由于转子一般以不平衡振动为主，转频即为激励频率，测试了转频ω为3.8 Hz和5.2 Hz时转子密封系统的振幅，研究了不同弹簧刚度下偏心自调结构对转子密封系统振动的抑制规律。

3.2.1 偏心自调结构固有频率测试

实验采用敲击法测试了五组不同弹簧刚度的偏心自调结构固有频率ω2，所使用的测试仪器为德国SCHENCK公司的SMARTBALANCER 现场动平衡仪中的撞击测试模块，其加速度传感器测量精度为6 000 m/s2(p-p) / ± 1%，可测频率范围为0.5 Hz～40 kHz。测试工况如图5所示，密封介质为水，密封内环外围均为空气。敲击测试中的加速度衰减曲线例如图6所示，测试所得固有频率数据如表1所示。

由表1可知，偏心自调结构的固有频率随弹簧刚度的增大而增大。由式(3)可知，该实验结果符合理论计算。

图5 偏心自调结构安装示意图Fig.5 Eccentricity self-adjusting structure installation schematic diagram

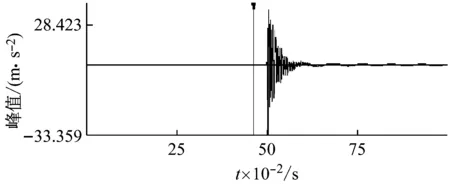
图6 偏心自调结构加速度衰减曲线Fig.6 Eccentricity self-adjusting structure acceleration attenuation curve

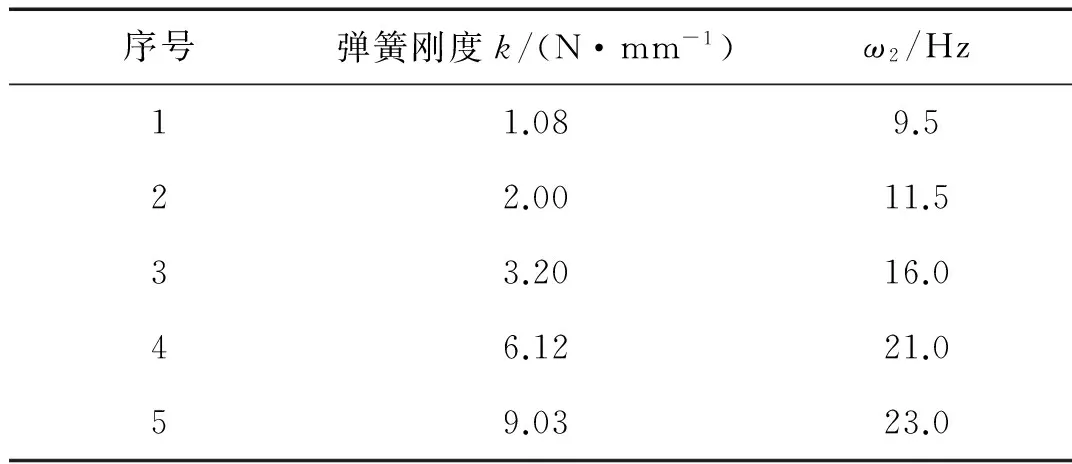
表1 偏心自调结构固有频率表Tab.1 Eccentricity self-adjusting structure natural frequency

3.2.2 转频3.8 Hz时偏心自调结构减振规律实验研究

对转子密封系统的原始振动和安装偏心自调结构后的振动情况进行实验研究。其中原始振动为未安装偏心自调结构时密封系统的振动，此时密封内环外不安装弹簧，周向用螺栓卡紧，使其固定不动，其他实验条件不变。实验得到了如表2所示的转子密封系统的振动情况。将表2中数据做成曲线图，如图7所示。频率比ω/ω2和对应的振动降幅随弹簧刚度的变化趋势如图8所示。

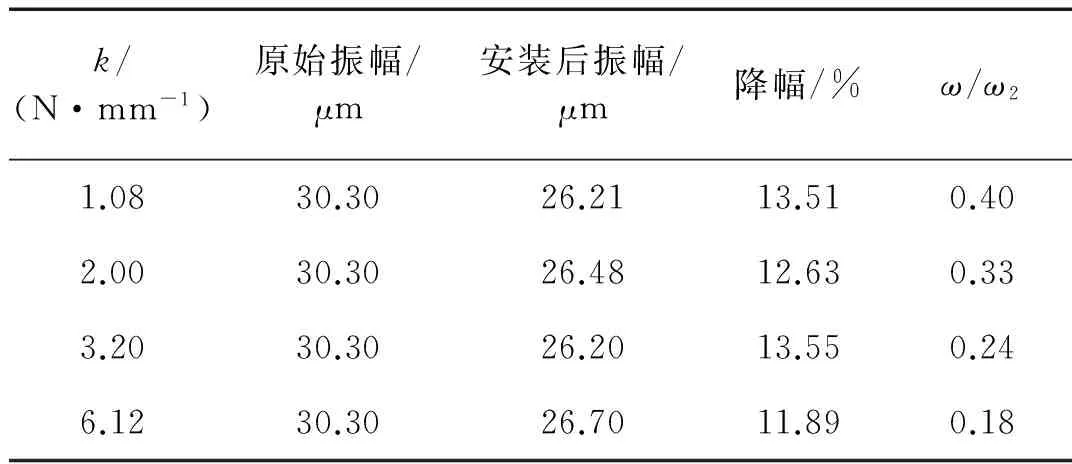
表2 转频为3.8 Hz时的振动数据Tab.2 The vibration data at rotating frequency 3.8 Hz

图7 转频为3.8 Hz时振幅随弹簧刚度变化曲线Fig.7 Vibration amplitude variation curve along with the spring stiffness at rotating frequency 3.8 Hz

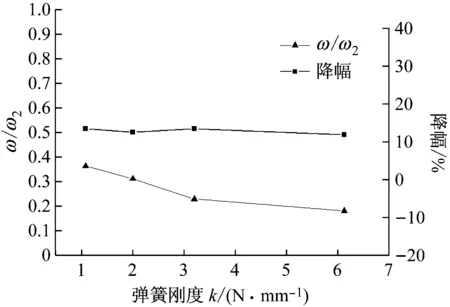
图8 转频为3.8 Hz时ω/ω2和降幅随弹簧刚度变化趋势Fig.8 ω/ω2 and amplitude decrease ratio variation curve along with the spring stiffness at rotating frequency 3.8 Hz

从图7中可以得知，安装偏心自调结构后的系统振幅较未安装时更小，偏心自调结构对转子密封系统的振动能够起到一定抑制作用。由图8可进一步看出，转子密封系统的振动降幅不大，仅维持在10%～15%。这是因为，频率比ω/ω2的值均在0.4以下，即ω和ω2相差较大，使得偏心自调结构对转子密封系统的影响较小，振动没有得到大幅传递，不能起到明显的抑振作用。

3.2.3 转频5.2 Hz时偏心自调结构减振规律实验研究

对转子在该转频下的原始振幅和安装偏心自调结构后的振幅进行实验研究，振动数据如表3所示。原始振幅和安装后振幅变化曲线如图9所示。ω/ω2和对应的振动降幅随弹簧刚度的变化趋势如图10所示。

从图9和图10中可以看出，转频5.2 Hz时，转子密封系统的振动得到了一定程度的抑制。但频率比ω/ω2的值在0.55以下，ω和ω2依然相差较远，转子密封系统的振动降幅也只维持在10%～20%，振动降幅随弹簧刚度变化不明显。

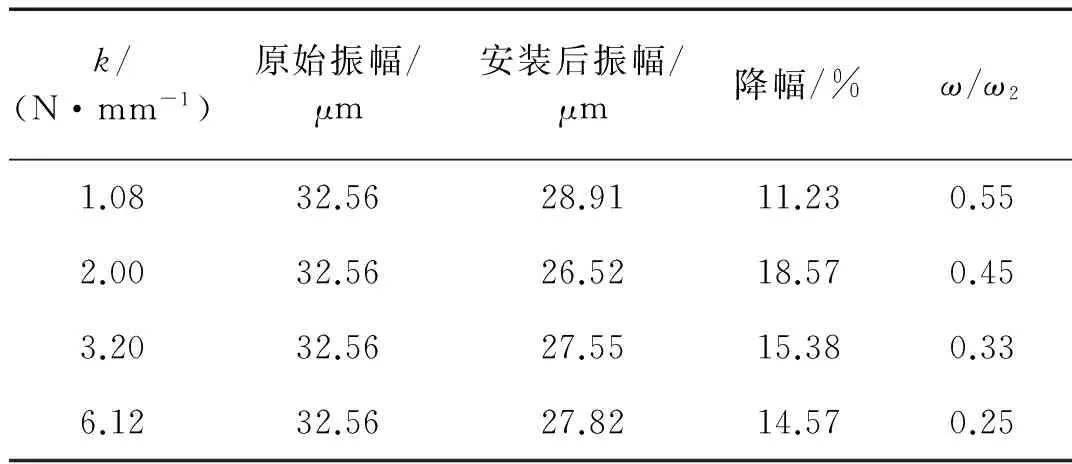
表3 转频为5.2 Hz时的振动数据Tab.3 Vibration data at rotating frequency 5.2 Hz

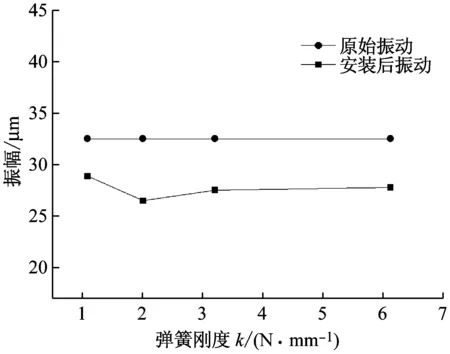
图9 转频为5.2 Hz时振幅随弹簧刚度变化曲线Fig.9 Vibration amplitude variation curve along with spring stiffness at rotating frequency 5.2 Hz

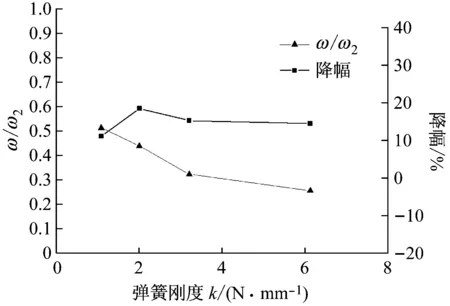
图10 转频为5.2 Hz时ω/ω2和降幅随弹簧刚度变化趋势Fig.10 ω/ω2 and amplitude decrease ratio trend along with the spring stiffness at rotating frequency 5.2 Hz

由以上实验结果可以得知，偏心自调结构能够对转子密封系统振动起到抑制作用，但振动降幅不甚明显，仅维持在10%～20%，振动降幅随弹簧刚度变化不大。其机理是由于激励频率ω与偏心自调结构固有频率ω2的比值均在0.55以下，1-(ω/ω2)2值较大，振动传递系数Tf较小，转子及流体传递到密封内环的振动较小，故减振效果不佳。

3.3密封偏心自调结构浸于水中时的减振规律实验研究

前文实验中转子的转频有3.8 Hz和5.2 Hz两种，且偏心自调结构的密封内环外围为空气，其固有频率远大于实验转频，两者差值较大，带来的减振效果并不明显。水作为附加质量[12]和阻尼元件[13]，对结构前五阶固有频率的影响因子c[14]一般为0.64～0.8，且会消耗一定的振动能量。故本文进一步考虑密封内环外围加水的影响，将偏心自调结构浸在水中，并增加一组转频为2.7 Hz的实验工况，进一步研究浸在水中的偏心自调结构对2.7 Hz、3.8 Hz和5.2 Hz三种转频下转子密封系统的减振规律。

3.3.1 密封偏心自调结构浸于水中时的固有频率测试

采用敲击法，对浸在水中的偏心自调结构进行模态测试，得到了其固有频率，实验工况如图11所示。将浸于水时偏心自调结构的固有频率用ω2w表示，测试数据如表4所示。表4中c=ω2w/ω2，为水对偏心自调结构固有频率的影响因子。

由表4可以看出，在所设计的几组弹簧中，偏心自调结构的固有频率仍然随弹簧刚度k的增大而增大，但是明显小于偏心自调结构在空气中时的固有频率ω2，水的影响影子c在0.6左右。水作为附加质量可以减小结构固有频率，这一结论再次得到验证，并且水对结构固有频率的影响因子与朱骁健等的试验结果较为接近。

图11 偏心自调结构浸于水示意图Fig.11 Eccentricity self-adjusting structure immersed in water schematic diagram

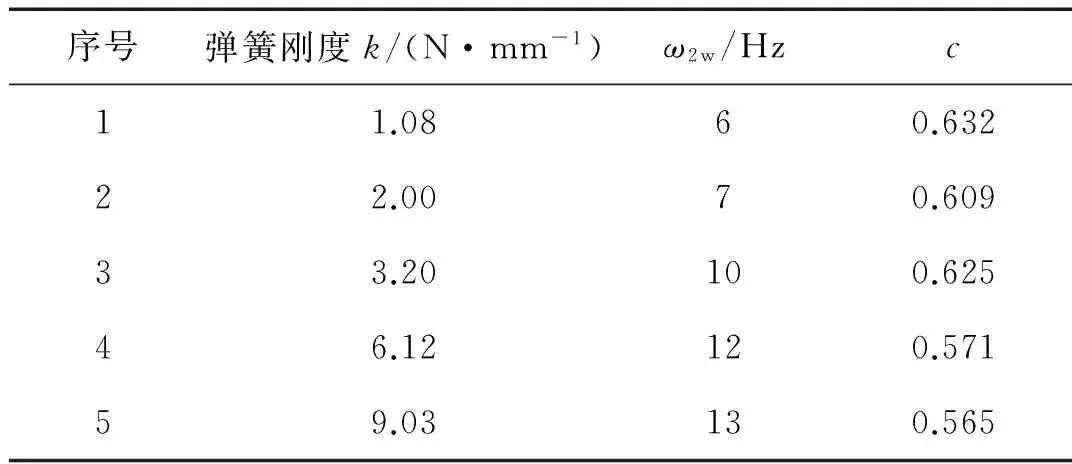
表4 浸于水时的偏心自调结构固有频率Tab.4 Eccentricity self-adjusting structure immersed in water frequency

3.3.2 转频为2.7 Hz时浸在水中的偏心自调结构减振规律实验研究

对转频2.7 Hz时的原始振幅和安装浸于水的偏心自调结构后转子密封系统的振幅进行实验研究，结果如表5所示。振幅随弹簧刚度的变化如图12所示。频率比ω/ω2w与对应的降幅随弹簧刚度的变化曲线如图13所示。

表5 转频为2.7 Hz偏心自调结构浸于水时的振动数据Tab.5 Vibration data at rotating frequency 2.7 Hz when structure immersed in water

图12 转频2.7 Hz结构浸于水时的振幅随弹簧刚度变化曲线Fig.12 Vibration amplitude variation curve along with spring stiffness at rotating frequency 2.7 Hz when the structure immersed in water

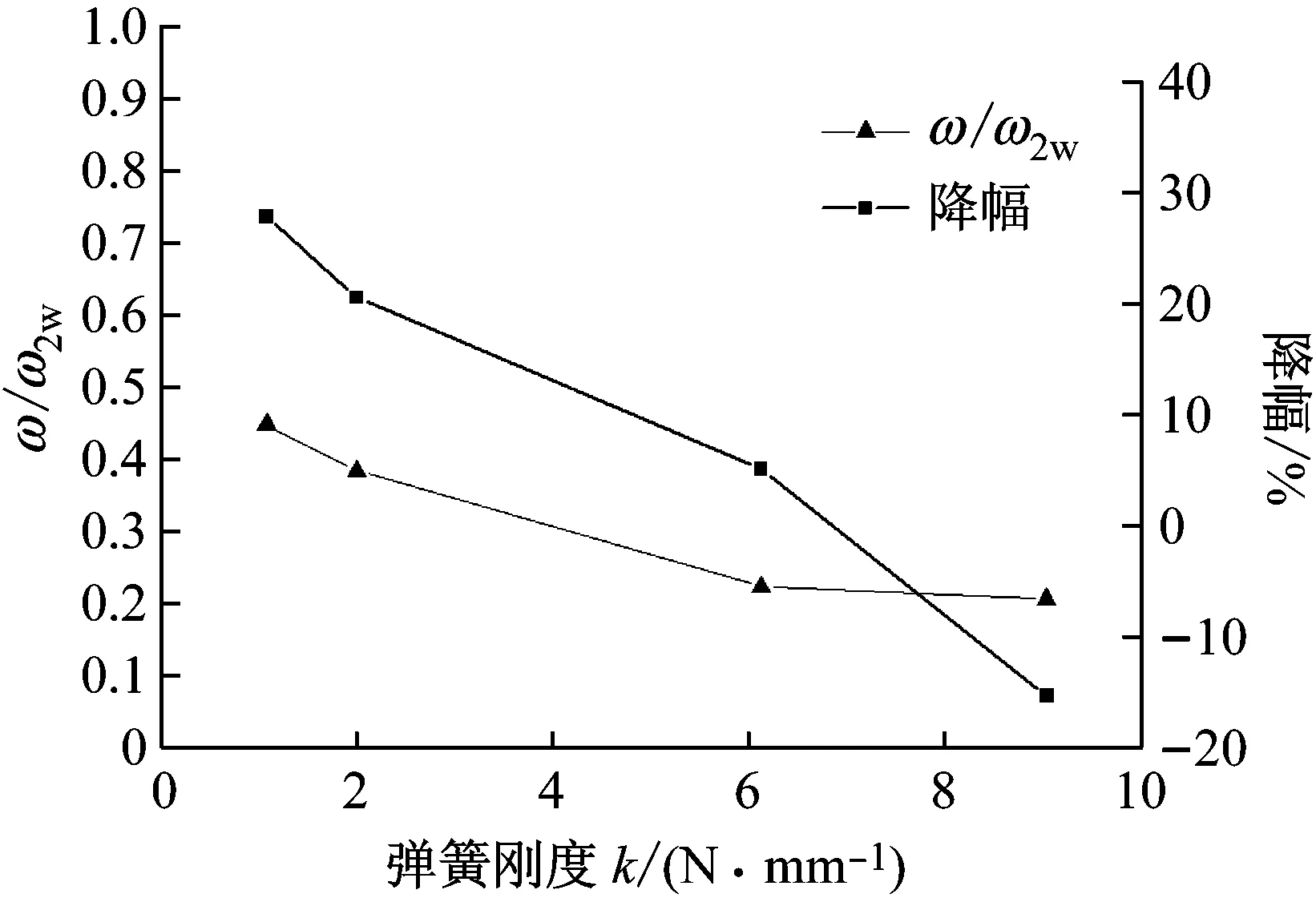
图13 转频为2.7 Hz时ω/ω2w和降幅随弹簧刚度变化趋势Fig.13 ω/ω2w and amplitude decrease ratio trend along with the spring stiffness at rotating frequency 2.7 Hz

由图12 可以看出，安装浸于水的偏心自调结构后，转子密封系统的振动成功得到抑制，并且随着弹簧刚度的减小，抑振效果加强。从图13中可以发现，随弹簧刚度减小，激励力频率ω与偏心自调结构的固有频率ω2w的比值逐渐接近0.5，系统的振动降幅随ω/ω2w的增大而增大，最大降幅为27.97%。

这一工况下的频率比ω/ω2w与转频为5.2 Hz、偏心自调结构密封内环外围为空气中时的几种频率比ω/ω2较为接近，但是抑振效果更好，分析认为其原因是密封内环外围的水作为阻尼元件，大大消耗了振动能量。

3.3.3 转频为3.8 Hz时浸在水中的偏心自调结构减振规律实验研究

对该转频下安装浸于水的偏心自调结构后不同弹簧刚度下的振幅进行测量，并与其原始振幅进行比较，结果如表6所示。转子密封系统的振幅变化曲线如图14所示。频率比ω/ω2w与降幅随弹簧刚度的变化趋势如图15所示。

表6 转频为3.8 Hz偏心自调结构浸于水时的振动数据Tab.6 Vibration data at rotating frequency 3.8 Hz when structure immersed in water

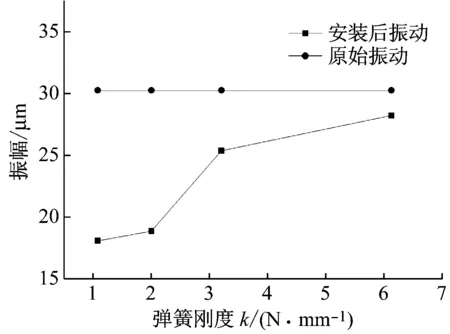
图14 转频3.8 Hz结构浸于水时的振幅随弹簧刚度变化曲线Fig.14 Vibration amplitude variation curve along with spring stiffness at rotating frequency 3.8 Hz when the structure immersed in water

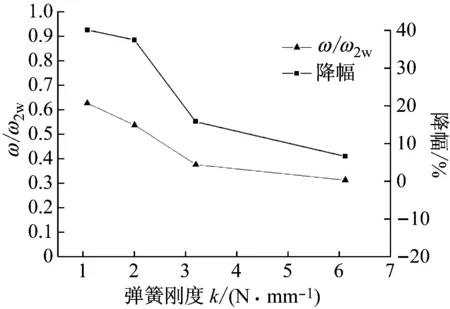
图15 转频为3.8 Hz时ω/ω2w和降幅随弹簧刚度变化趋势Fig.15 ω/ω2w and amplitude decrease ratio trend along with the spring stiffness at rotating frequency 3.8 Hz

图14表明，转子密封系统的振动得到了明显抑制，降幅随弹簧刚度的减小而增大。刚度为1.08 N/mm时降幅最大，抑振效果最好；而刚度为9.03N/mm时的振幅接近原始振动幅值。由图15可以看出，随弹簧刚度减小，ω/ω2w逐渐增大到0.63，更接近1，振动降幅也随之增大，最大为40.03%。ω/ω2w越接近1，1-(ω/ω2)2越小，振动传递系数Tf越大，所以减振效果越好，这一实验现象符合理论分析。

3.3.4 转频为5.2 Hz时浸在水中的偏心自调结构减振规律实验研究

同样对该转频下安装浸于水的偏心自调结构后不同弹簧刚度下的振幅变化进行研究，结果如表7所示。将表7中的振动数据做成曲线图，如图16所示。此时频率比ω/ω2w与振动降幅随弹簧刚度的变化趋势如图17所示。

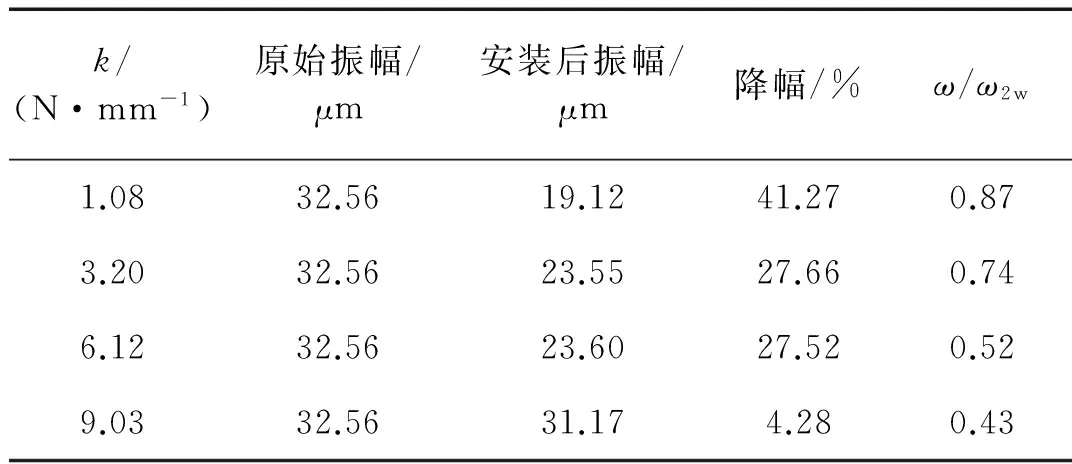
表7 转频为5.2 Hz偏心自调结构浸于水时的振动数据Tab.7 Vibration data at rotating frequency 5.2 Hz when structure immersed in water

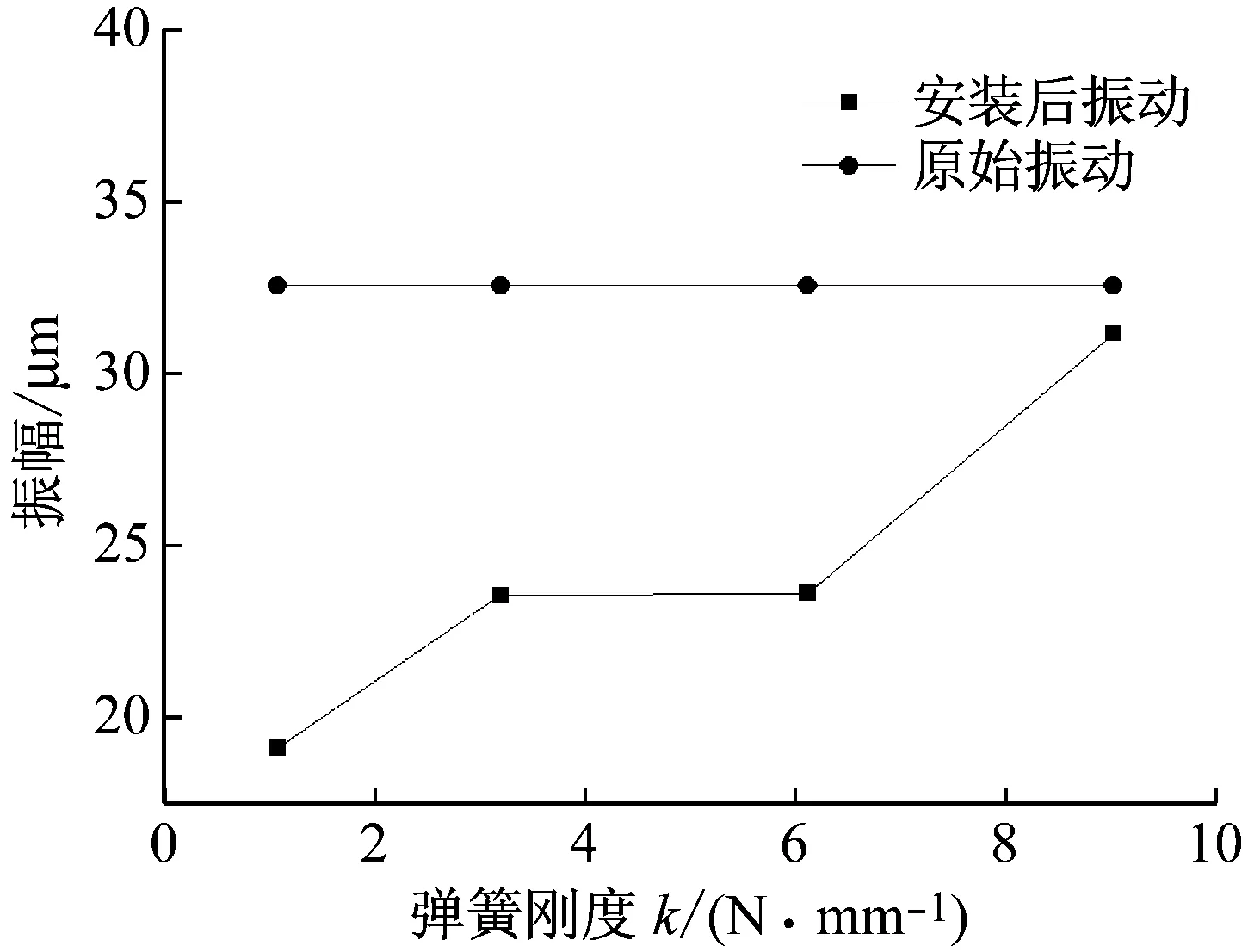
图16 转频5.2 Hz结构浸于水时的振幅随弹簧刚度变化曲线Fig.16 Vibration amplitude variation curve along with spring stiffness at rotating frequency 5.2 Hz when the structure immersed in water

由图16可以看出，安装浸于水的偏心自调结构后，转子密封系统的振动得到了大幅抑制，降幅依然随弹簧刚度的减小而增大。由图17知，随弹簧刚度减小，ω/ω2w值逐渐接近1，最大为0.87，振动降幅随之增大，最大为41.27%。原因是弹簧刚度k的减小使得偏心自调结构的固有频率ω2w越小，更为接近激励频率ω，两者的吻合使该结构的抑振效果达到最好。

以上实验结果表明，密封偏心自调结构浸在水中时，对转子密封系统的振动能够起到显著的抑制作用，且减振效果随弹簧刚度的变化较大。当弹簧刚度的变化使偏心自调结构的固有频率ω2w越接近激励频率ω，1-(ω/ω2)2值越小，振动传递系数Tf越大，振动能量传递越多，其抑振效果越好；反之，效果减弱。其中转频为5.2 Hz、弹簧刚度为1.08 N/mm时，ω/ω2w=0.87，1-(ω/ω2)2最小，振动降幅最大，为41.27%，结果与理论分析一致。

图17 转频为5.2 Hz时ω/ω2w和降幅随弹簧刚度变化趋势Fig.17 ω/ω2w and amplitude decrease ratio trend along with the spring stiffness at rotating frequency 5.2 Hz

4 结 论

针对由转子偏心引起的密封流体激振问题，本文设计了一种新型偏心自适应调节密封结构，对该结构的减振机理进行了探究，对其在不同工况下的固有频率进行了测试，研究了不同弹簧刚度和转频下该结构的抑振效果，获得以下结论：

(1) 所设计的偏心自调结构的减振效果与其激励频率和固有频率的比值ω/ω2有关，ω/ω2比值越接近1，减振效果越显著。

(2) 密封内环外围为空气时，偏心自调结构的固有频率ω2随弹簧刚度k的增大而增大。安装偏心自调结构后，转子密封系统的振动得到一定抑制。但由于频率比ω/ω2值与1差距较大，ω/ω2值的变化对降幅的影响不明显，降幅只维持在10%～20%。

(3) 偏心自调结构浸在水中时，其固有频率ω2w随弹簧刚度k的增大而增大，但均小于在空气中时的固有频率ω2。并且同频率比时，浸于水的偏心自调结构减振效果更好。原因是水作为附加质量减小了偏心自调结构的固有频率；作为阻尼元件，增加了振动能量的消耗。

(4) 安装浸于水的偏心自调结构后，由于ω/ω2w的值较接近1及水阻尼的耗能作用，转子密封系统的振动得到明显抑制，振动降幅最大达到41.27%。反之当ω/ω2w越远离1，振动降幅则越小，该实验结果符合理论分析。

[1] 陈佐一．流体激振[M]. 北京：清华大学出版社，1998．

[2] CHILDS D W. Test results for round-hole-pattern damper seals: optimum configurations and dimensions for maximum net damping[J]. Journal of Tribology，1986，108(4)：605-609．

[3] CHILDS D W，SHIN Y S, SEIFERT B. A design to improve the effective damping characteristics of hole-pattern-stator annular gas seals[J]. Journal of Engineering for Gas Turbines and Power，2008，130(1)：012505.

[4] NIELSEN K K，JØNCK K，UNDERBAKKE H. Hole-pattern and honeycom-b seal rotordynamic forces: validation of CFD-based predic-tion techniques[J]. Journal of Engineering for Gas Turbines and Power，2012，134(12)：122505-122514.

[5] DA SOGHE R，MICIO M，ANDREINI A，et al．Numerical Characterization of swirl brakes for high pressure centrifugal compressor[C]∥ASME Turbo Expo 2013: Turbine Technical Conference and Exposition．San Antonio：ASME，2013.

[6] CHILDS D W，MCLEAN J E，ZHANG M, et al. Rotordynamic performance of a negative-swirl-brake for a tooth-on-stator labyrinth seal[J]. Journal of Engineering for Gas Turbines and Power，2016，138(6)：062505.

[7] 吕成龙，何立东，涂霆. 反旋流抑制转子不平衡实验研究[J]. 液压气动与密封，2014，34(11)：16-18.

LÜ Chenglong, HE Lidong，TU Ting．Experimental study on suppressing the rotor unbalance with anti-swirl flow[J]．Hydraulics Pneumatics& Seals，2014，34(11)：16-18.

[8] 尹德志．密封腔吸水及可控吸气的减振实验研究[D]．北京：北京化工大学，2010．

[9] 罗振兵．合成射流流动机理及应用技术研究[D]．长沙：中国人民解放军国防科学技术大学，2002．

[10] GAMAL A J M, VANCE J M. Labyrinth seal leakage tests: tooth profile, tooth thickness, and eccentricity effects[J]. Journal of Engineering for Gas Turbines and Power，2008，130(1)：012510-012520.

[11] 孙京平，王开和，卢学军，等．水泵的双层隔振设计[J]. 机械设计与制造，2006(3)：5-7．

SUN Jingping，WANG Kaihe，LU Xuejun, et al．Design of water pump on two layers vibration isolation experiment[J]．Machinery Design &Manufacture，2006(3)：5-7．

[12] 张兆龙，高博青，杨宏康. 基于附加质量法的大型固定顶储液罐基底隔震分析[J]. 振动与冲击，2012，31(23): 31-38．

ZHANG Zhaolong，GAO Boqing，YANG Hongkang．S-eismic analysis of a large base-isolated liquid storage tank with fixed roof based on added mass method[J] ．Journal of Vibration and Shock，2012，31(23): 31-38．

[13] 朱骁健，杜成斌，陈玉泉．考虑库水阻尼耗能的重力坝地震响应分析[J]. 水电能源科学，2015，33(8)：72-74．

ZHU Xiaojian，DU Chengbin, CHEN Yuquan．Seismic response analysis of gravity dam considering damping of reservoir water[J]．Water Resources and Power，2015，33(8)：72-74．

[14] 张丽霞，张伟，潘际銮．基于流固耦合理论的混流式叶片动力学分析[J]．清华大学学报(自然科学版)，2008，48(5)：774-776．

ZHANG Lixia，ZHANG Wei, PAN Jiluan．Dynamic analysis of a francis turbine based on the fluid-structure interaction theorem[J]． Journal of Tsinghua University(Science and Technology)，2008，48(5)：774-776．

Newmethodfortheself-adjustingofsealeccentricityandexperimentalresearchonthesealvibrationcontrol

LI Kuan，HE Lidong，TU Ting

(Diagnosis and Self-recovering Research Center, Beijing University of Chemical Technology, Beijing 100029, China)

Aiming at reducing the seal fluid excitation caused by rotor eccentricity, a new eccentricity self-adjusting seal structure which can decrease the rotor eccentricity was designed and its vibration suppression mechanism was explored. It is concluded by the theoretical analysis that the vibration suppression effect will be the best only when the natural frequency of the designed structure is consistent with the rotor-seal exciting frequency. Using water as the sealing media, the natural frequencies of the designed structure with different spring stiffness were measured respectively. Changing the rotating frequency, the structural vibration suppression effect was experimentally investigated. The results show that the structural frequency increases with the increase of spring stiffness, but is much higher than the rotor-seal exciting frequency. The vibration amplitude reduction ratio is not notable, only between 10%～20%. Then the eccentricity structure was put into the water, its frequency in water was measured. and its vibration suppression effect in water was experimentally researched. The results demonstrate that the structural frequencies in water still increase with the increase of spring stiffness but are about 40% lower than in the air. So, the structural frequency in water is closer to the exciting frequency and the vibration suppression effect in this condition is more obvious. The maximum vibration amplitude reduction ratio reaches 41.27%.

non-contact seal；seal fluid excitation；rotor eccentricity self-adjusting；natural frequency

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.19.008

国家重点基础研究发展计划项目(973计划)(2012CB026000)；高等学校博士学科点专项科研基金资助课题(20110010110009)

2016-06-13 修改稿收到日期：2016-08-06

李宽 女，硕士生，1992年生

何立东 男，博士，研究员，博士生导师，1963年生