基于能量法的调谐黏性质量阻尼器地震响应预测式研究
2017-11-06裴星洙邱吉祥伏恬甜
裴星洙,邱吉祥,伏恬甜
(1. 江苏科技大学 土木工程与建筑学院,江苏 镇江 212003; 2. 江苏筑森建筑设计股份有限公司,江苏 常州 213000)
基于能量法的调谐黏性质量阻尼器地震响应预测式研究
裴星洙1,邱吉祥2,伏恬甜1
(1. 江苏科技大学 土木工程与建筑学院,江苏 镇江 212003; 2. 江苏筑森建筑设计股份有限公司,江苏 常州 213000)
建立附加调谐黏性质量阻尼器的多层钢框架结构,简要分析其力学模型。建立能量平衡方程,并给出主结构弹性振动能、阻尼器弹性振动能、阻尼器黏性阻尼耗能的表达式,推导出剪力系数和层间位移的预测式。提出质量阻尼能量分散系数和黏性阻尼能量分散系数的简化计算公式。利用时程分析法验证了预测式和简化计算公式的准确性。利用位移降低率和剪力降低率的不同线性组合得出不同使用要求下的阻尼器优化置放量。结果表明:① 简化计算公式能够近似地计算能量分散系数;② 本文的预测式包络时程分析法的结果,能够比较准确地预测结构的地震反应;③ 当采用优化分布规律,质量比为0.2,刚度比为0.8,阻尼器阻尼比为0.8时,各种使用要求下的减震效果最佳。
调谐黏性质量阻尼器;能量平衡方程;预测式;简化计算公式;能量分散系数;优化置放量
地震作用实际上是一种能量的输入、转化和消耗的过程[1],基于能量平衡的分析方法(简称能量法)从体系自身的能量消耗能力出发,综合考虑了结构自身的特性和地震运动的特点,对结构体系在地震作用过程中的安全性作出评价[2-3]。对于布置耗能阻尼器的结构,能量分析能更好地反映耗能阻尼器的工作效率[4]。
目前比较常见的阻尼器可以分为速度相关型阻尼器和位移相关型阻尼器[5],而调谐黏性质量阻尼器(Tuned Viscous Mass Damper, TVMD)是一种加速度相关型阻尼器,该阻尼器由滚珠丝杠副、内筒、外筒、质量块和黏弹性材料组成,利用滚珠丝杠副将水平运动转化为转动,在内筒和外筒之间填充黏弹性材料,消耗地震动输入的能量。井上範夫等[6]提出了调谐黏性质量阻尼器,介绍了其工作原理,并研究了其在地震动作用下的地震反应。文献[7]研究了单质点结构附加调谐黏性质量阻尼器在简谐波作用下的理论地震反应值,并提出了优化的设计参数。磯田和彦等[8]提出了不同阻尼器安装方案下的地震动输入能量计算公式。该阻尼器是日本学者近年提出的一种新型阻尼器,目前关于该阻尼器基于能量法的研究还比较少见。
在设计阻尼器时,需要进行多次的地震响应时程分析,利用所得到的层间剪力和层间位移等响应值,选择最合适的阻尼器参数。这样计算不仅耗费大量的时间和精力,而且如果最初的估计和预料偏差较大的话,还可能陷入设计值不收敛的情况。为了避免这种情况发生,在进行地震响应分析时程分析之前,我们可以利用简便的响应预测式,预先进行粗略的设计。本文提出的基于能量法的调谐黏性质量阻尼器的设计方法是该种阻尼器的一种简化设计方法,在具体的阻尼器设计之前,可以采用该方法进行粗略的设计,大大减少了阻尼器设计的工作量。
本文建立了附加调谐黏性质量阻尼器的钢框架结构在地震作用下的能量平衡方程,推导出该体系的地震响应预测式,并拟合了能量分散系数的简化计算公式。利用时程分析法验证了预测式和简化计算公式的准确性。最后分析了不同使用要求下的阻尼器优化置放量。
1 分析模型
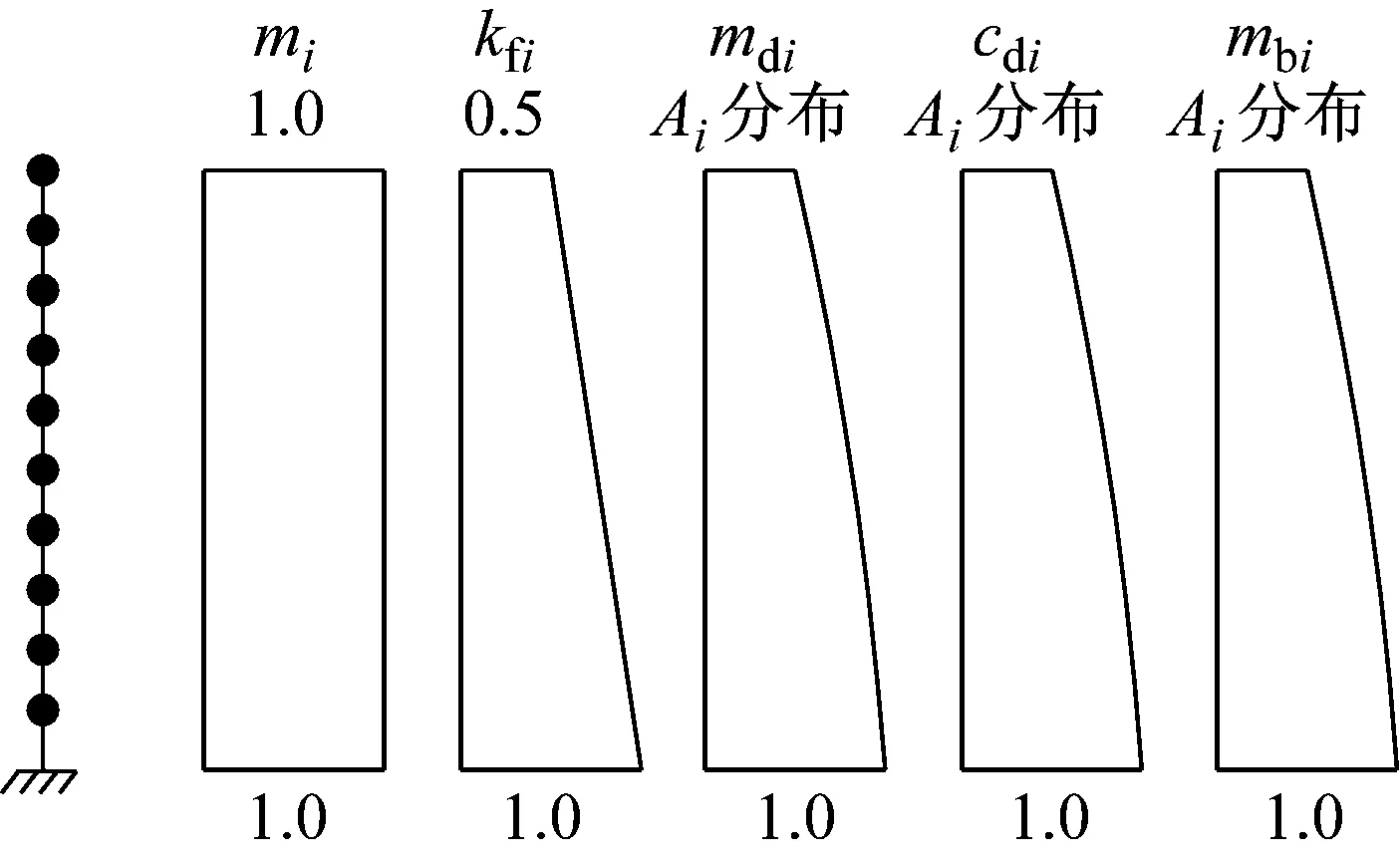
本文讨论多质点剪切型模型,在每一楼层上都附加调谐黏性质量阻尼器,计算模型如图1所示,m为主结构的质量,cf为主结构的阻尼系数,kf为主结构的水平抗侧刚度,cd为TVMD的等效阻尼系数,md为TVMD的等效质量,kb为支撑的抗侧刚度。如图2所示,TVMD由黏性阻尼和质量阻尼两部分并联组成,TVMD与支撑串联形成附加结构,附加结构与主结构并联形成计算模型,xd为阻尼器的水平相对位移,xb为支撑的水平相对位移,x为主结构的水平层间位移。在地震作用下,阻尼器消耗能量,主结构消耗的能量很少,认为主结构始终处于弹性状态;TVMD的恢复力模型如图3(a)所示,其可以分解为如图3(b)和图3(c)所示的两部分,Qd为TVMD的阻尼力,Qc为TVMD的黏性阻尼力,Qm为TVMD的质量阻尼力,xd,max为阻尼器的相对水平位移,ω为主结构的第一自振圆频率。附加结构与主结构并联,故附加结构的水平相对位移等于主结构的水平层间位移。阻尼器与支撑串联,故阻尼器的力等于支撑的力。为了保证阻尼器正常工作,支撑的刚度通常远大于阻尼器的等效刚度,故可以认为支撑的水平相对位移远小于阻尼器的水平相对位移。为简化计算,本文忽略支撑的水平相对位移,近似地认为xd,max=xmax。

图1 多质点体系模型计算简图Fig.1 Multi-mass models
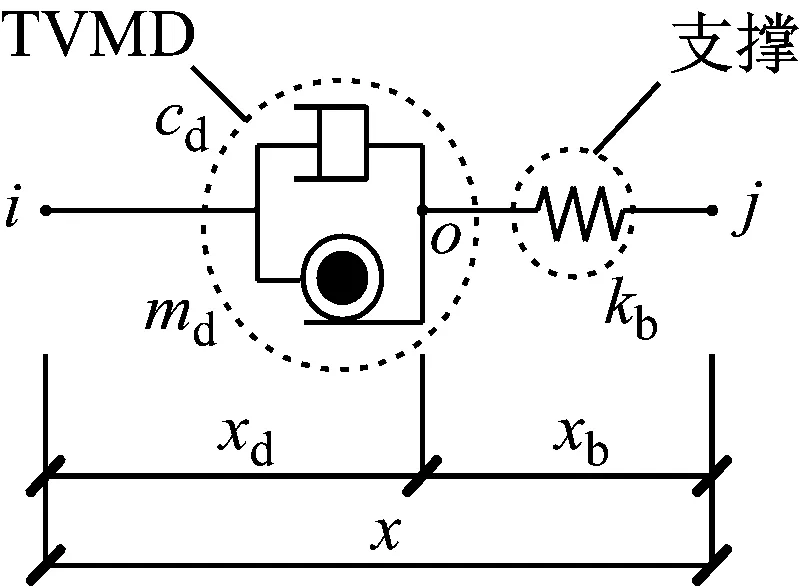
图2 附加结构计算简图Fig.2 Additional structure
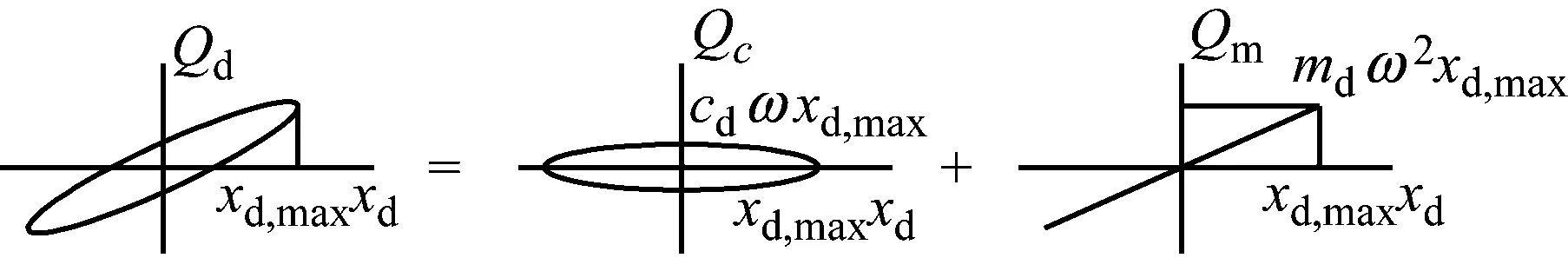
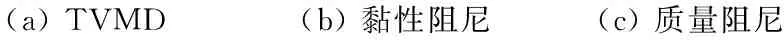
(a)TVMD (b)黏性阻尼 (c)质量阻尼
2 能量平衡方程
发生地震时,该体系的能量平衡方程为
(1)
式中:We为主结构的弹性振动能;Wh为主结构消耗的阻尼能;dWe为TVMD质量阻尼的弹性振动能;dWh为TVMD黏性阻尼消耗的阻尼能;Ein为地震动输入的能量;M为主结构的总质量;VE为能量谱速度换算值。
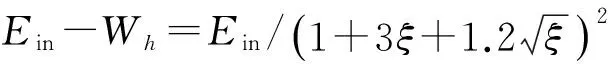
(2)
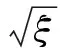
3 地震反应预测式的推导
3.1主结构弹性振动能
主结构第i层的弹性振动能为
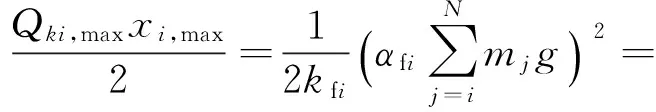
(3)
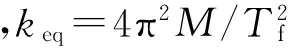
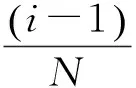
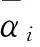
把主结构每层的弹性振动能累加,即为主结构的弹性振动能
(4)
式(4)可以近似地表示为
(5)
3.2阻尼器耗能
第i层的TVMD弹性振动能为
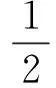
(6)
式中:Qmi,max为第i层TVMD的最大质量阻尼力;xdi,max为第i层TVMD两端的最大水平位移;αmi为第i层TVMD质量部分的剪力系数。
将所有TVMD弹性振动能与第k层的TVMD弹性振动能的比值,定义为第k层的质量阻尼能量分散系数γmk,则
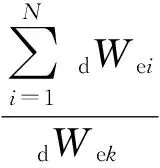
(7)
式中:dWek为第k层的TVMD弹性振动能;mdk为第k层TVMD的等效质量。
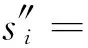
(8)
所有TVMD弹性振动能为
(9)
第i层TVMD的黏性阻尼耗能为
dWhi=πQci,maxxdi,maxn1=
(10)
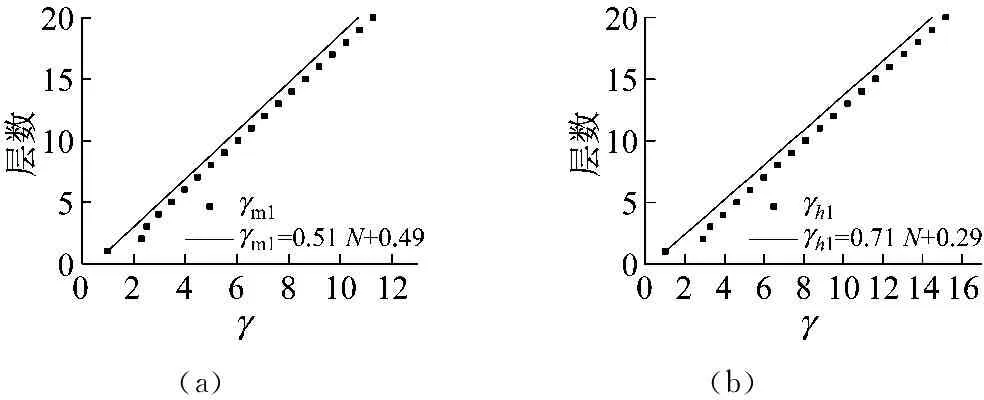
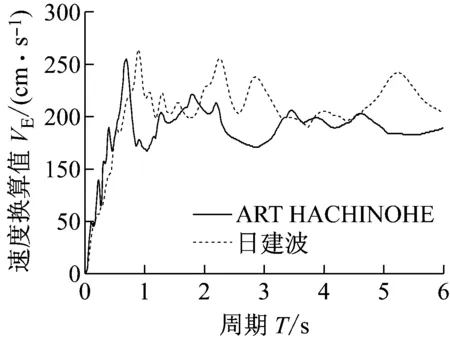
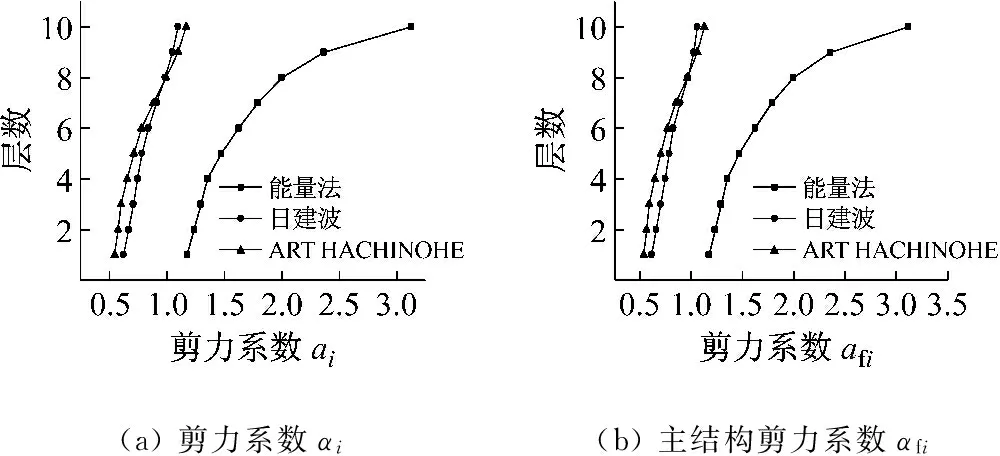
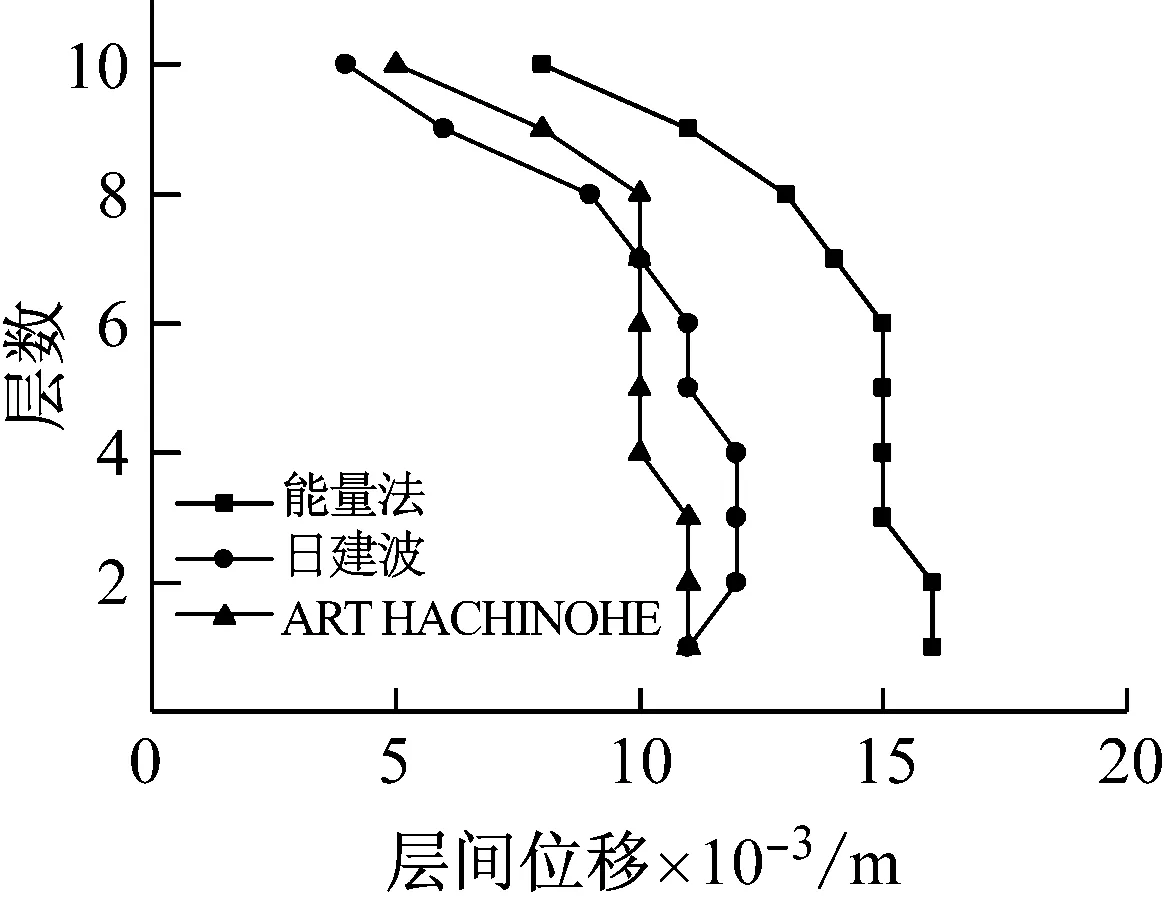
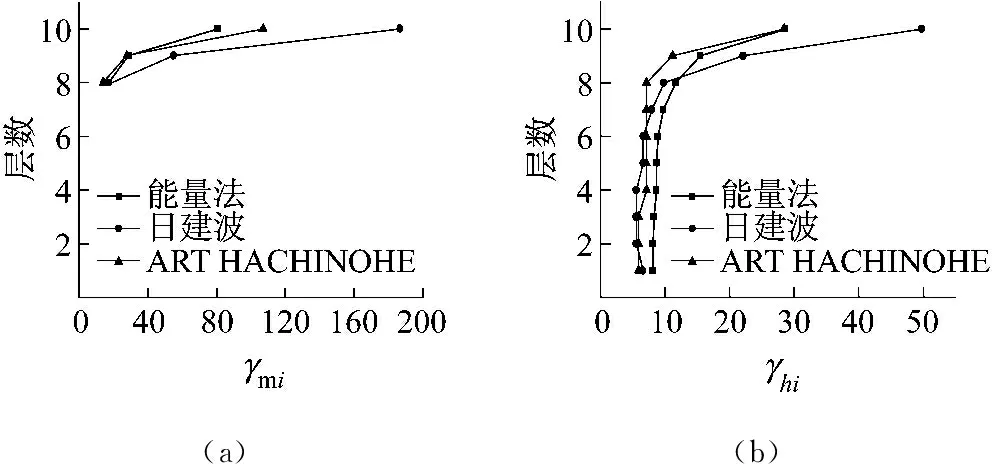
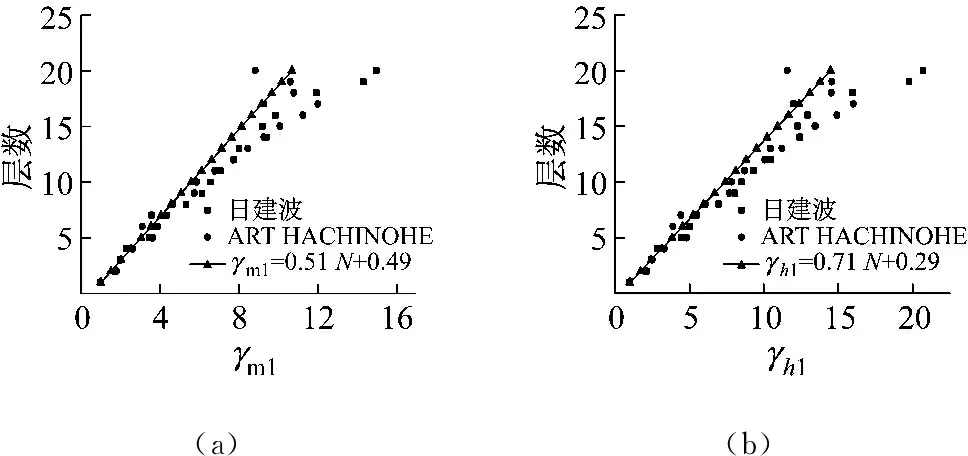
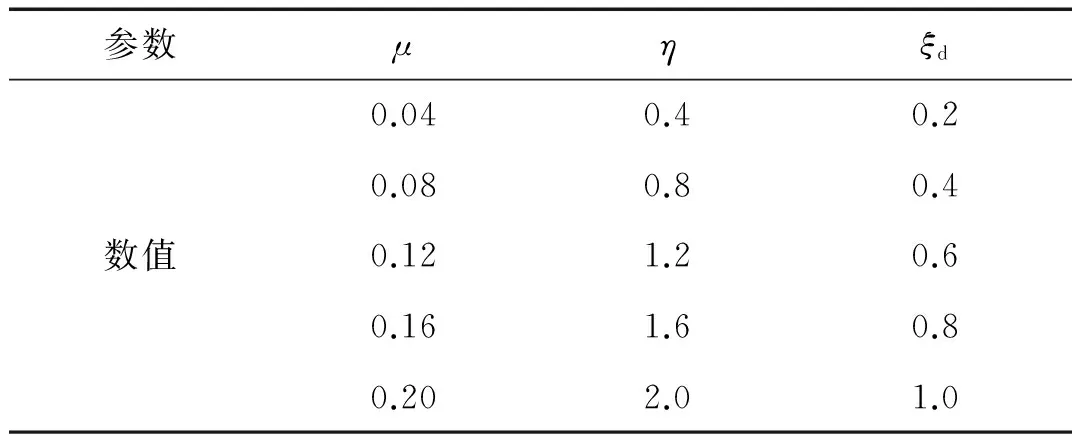
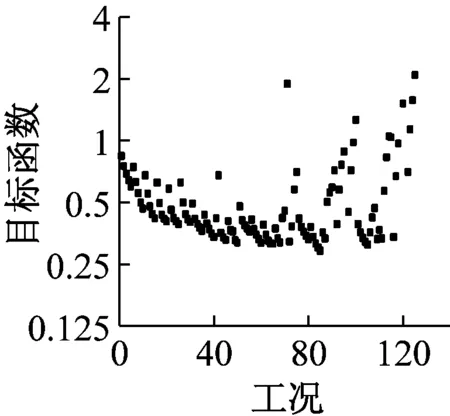
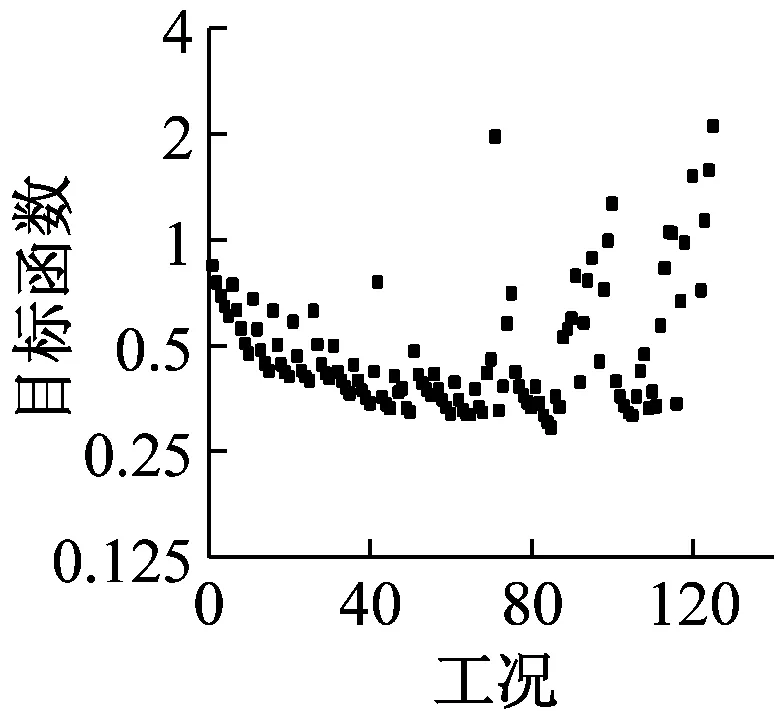
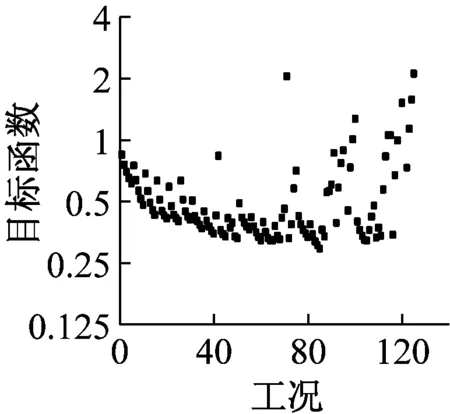
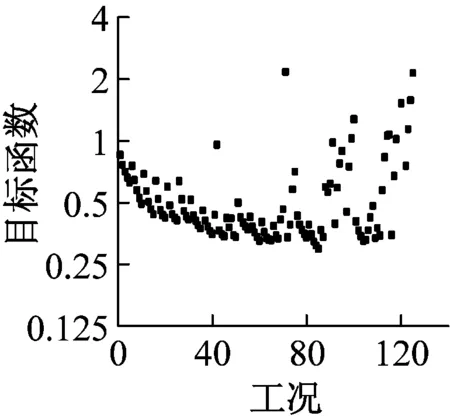
式中:Qci,max为第i层TVMD的最大黏性阻尼力;n1为等价黏性滞回系数[9],当Tf<5 s时,n1=2,当Tf>8 s时,n1=1,当5 s 将所有TVMD黏性阻尼耗能与第k层的TVMD黏性阻尼耗能的比值,定义为第k层的黏性阻尼能量分散系数γhk[10],则 (11) 式中:dWhk为第k层的TVMD黏性阻尼耗能;hdk为第k层TVMD黏性阻尼的阻尼比。 (12) 所有TVMD的黏性阻尼耗能为 dWh=γhi·dWhi= (13) 3.3能量平衡方程 将式(5)、式(9)、式(13)代入式(2)中,得 (14) (15) 从图3的恢复力模型可知 (16) (17) 由式(16)和式(17)可知 (18) (19) 将式(18)和式(19)代入式(15)中,可以得出 (20) 由于主结构和TVMD质量阻尼与黏性阻尼存在π/2的相位差,故层间剪力的最大值可采用式(21)计算 (21) 计算模型底层的剪力系数表示为 (22) 将式(18)~式(20)代入式(22)中,得 (23) 底层的层间位移最大值表示为 (24) 式中,x0=α0Mg/keq=TfVD/2π。 γm1、γh1均为计算时的重要参数,由式(7)和式(8)得 (25) 由式(11)和式(12)得 (26) 其中, (27) (28) γm1=0.51N+0.49 (29) γh1=0.71N+0.29 (30) 图4 结构参数分布图Fig.4 Distribution of structural parameters (a)(b) 5.1地震波的选取 以地震动能量谱速度换算值VE(VE=150 cm/s2,二类场地,罕遇地震波)作为目标,选取日建波和ART HACHINOHE两条人工地震波,日建波时间间隔0.01 s,作用时间80 s,ART HACHINOHE时间间隔0.01 s,作用时间300 s。图6所示为地震动加速度时程曲线,图7为能量谱。从图7中可以看出,两条人工地震波的速度换算值均为150 cm/s2。 (a)日建波(b)ARTHACHINOHE 图7 能量谱Fig.7 Energy spectrum 5.2算例模型 为了评价能量法的准确性,本文建立附加TVMD的10层钢框架模型,主结构的质量和抗侧刚度见表1,主结构的阻尼比为0.02,层高为3 m。假定底层阻尼器的等效质量取为主结构底层质量的0.2倍,底层的支撑刚度取为主结构底层抗侧刚度的0.2倍,阻尼器的阻尼比为0.3,各层阻尼器的等效质量、支撑刚度采用Ai分布,数值见表1。采用自编Fortran程序,计算剪力系数和层间位移。 图8为剪力系数,从图中可以看出: (1) 能量法预测的剪力系数大于时程分析法算出的剪力系数,但两者的趋势相同,均为层数越高,剪力系数越大; (2) 两条不同的地震波作用下,剪力系数基本一致,趋势均为层数越高,剪力系数越大。 (a)剪力系数αi(b)主结构剪力系数αfi 图9为层间位移,从图中可以看出: (1) 能量法预测的层间位移大于时程分析法算出的层间位移,但两者的趋势相同,均为层数越高,层间位移越小; (2) 不同的地震波作用下,层间位移基本一致,趋势均为层数越高,层间位移越小; (3) 1层~8层的层间位移基本相同,9层和10层的层间位移较小,说明该阻尼器的布置形式基本合理,但结构上层的阻尼器可适当削弱。 图9 层间位移Fig.9 Story drifts 图10为阻尼器的能量分散系数,从图中可以看出: (1) 能量法预测的能量分散系数与时程分析法算出的能量分散系数基本一致; (2) 1层~8各层的能量分散系数基本一致,9层和10层的能量分散系数较小,说明该阻尼器的布置形式基本合理,但结构上层的阻尼器可适当削弱。 主结构和阻尼器采用与10层模型相同的布置规律,建立第四节中20种不同的算例模型并进行时程分析,图11为20种不同模型程序计算得出的结果,从图中可以看出式(29)和式(30)能较好的满足程序计算得出的结果,说明式(29)和式(30)是合理的近似计算公式。 (a)(b) 表1 模型参数Tab.1 Model parameters (a)(b) 通过以上的分析可以看出: (1) 能量法计算的最大水平层间位移和剪力系数包络时程分析法计算的最大水平层间位移和剪力系数,具有较好的精确性; (2) 式(29)和式(30)能够近似地代替式(25)和式(26),大大简化了计算; (3) 按照Ai规律布置阻尼器时,最大层间位移基本一致,说明该布置形式合理。 定义位移降低率为Rdi=xi,max/x0,剪力降低率为Rai=αfi/α0。为了确定阻尼器的置放量,本文以位移降低率和剪力降低率为控制目标,提出可满足不同需求的目标函数。以位移降低率和剪力降低率的线性组合为目标函数,所需的优化设计即是使目标函数最小的阻尼器布置方式[11],本文中定义目标函数为 Δ=min(a·Rd,max+b·Ra,max) (31) 式中:a为位移降低率的加权系数;b为剪力降低率的加权系数;Rd,max为最大位移降低率;Ra,max为最大剪力降低率。a、b可以根据不同要求取不同加权系数,具体数值如表2。 表2 目标函数加权系数Tab.2 Weighting coefficients of objective functions 定义质量比为μ=md1/m1,刚度比为η=kb1/kf1,其中:md1为底层附加阻尼器的等效质量,m1为结构底层的质量,kb1为底层支撑的水平抗侧刚度,kf1为结构底层的水平抗侧刚度。基于阻尼器优化设计的目标函数,分别布置不同规格的阻尼器,其参数的取值见表3,将3种参数组合,共有125种工况。 表3 阻尼器参数Tab.3 Damper parameters 图12为日建波和ART HACHINOHE波作用下,125种工况的最大位移降低率和最大剪力降低率的均值,从图中可以看出:工况85的最大位移降低率和最大剪力降低率同时达到最小值,此时,μ=0.2,η=0.8,ξd=0.8。 (a)(b) (a) 组合1 (b) 组合2 (c) 组合3 (d) 组合4 (e) 组合5图13 目标函数Fig.13 Objective functions 图13为5种组合的目标函数值,从图中可以看出:组合1~组合5中,工况85的目标函数达到最小值,此时,μ=0.2,η=0.8,ξd=0.8。 本文采用能量法,推导出附加调谐黏性质量阻尼器的多层钢框架结构的剪力系数和层间位移预测式。本文拟合了质量阻尼能量分散系数和黏性阻尼能量分散系数的简化公式,并采用时程分析法进行验证。利用本文提出的预测式和时程分析法分别计算了该结构的地震响应值,并将两者进行了比较分析。利用位移降低率和剪力降低率的不同线性组合得出不同使用要求下的阻尼器优化置放量。得到以下结论: (1) 简化计算公式能够近似地计算质量阻尼能量分散系数和黏性阻尼能量分散系数。 (2) 本文提出的预测式包络时程分析法的结果,能够比较准确地预测结构的地震反应。 (3) 按照Ai规律布置阻尼器时,最大层间位移基本一致,说明该布置形式合理。 (4) 当质量比μ=0.2,刚度比η=0.8,阻尼器阻尼比ξd=0.8时,各种使用要求下的结构减震效果最佳。 [1] 裴星洙,王维,王星星. 基于能量原理的隔震结构地震响应预测法研究[J]. 工程力学,2011,28(7):65-72. PEI Xingzhu, WANG Wei, WANG Xingxing. Earthquake response prediction of isolated structures based on energy principle[J]. Engineering Mechanics, 2011, 28(7): 65-72. [2] 北村春幸. 基于性能设计的建筑振动解析[M]. 裴星洙,廖红建,张立,译. 西安: 西安交通大学出版社,2004. [3] 秋山宏.基于能量平衡的建筑结构抗震设计[M]. 叶列平,裴星洙,译.北京:清华大学出版社,2010. [4] 彭泽靖,张洵安,连业达,等.基于能量分析的MSCSS附加阻尼器参数研究[J]. 地震工程与工程振动,2014,34(3):183-190. PENG Zejing, ZHANG Xun’an, LIAN Yeda, et al. Study on the additional damper parameters of MSCSS based on energy analysis[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(3): 183- 190. [5] 日本隔振构造协会. 被动减震结构设计施工手册[M]. 北京: 中国建筑工业出版社, 2008. [6] 井上範夫,五十子幸樹. 建築物の変位制御設計[M].东京:丸善出版株式会社,2012. [7] 邱吉祥,裴星洙.调谐黏性质量阻尼器减震性能研究[J].工程抗震与加固改造,2016,38(1):65-71. QIU Jixiang,PEI Xingzhu. Study on seismic performance of tuned viscous mass damper (TVMD)[J]. Earthquake Resistant Engineering and Retrofitting, 2016, 38(1): 65-71. [8] 磯田和彦,半澤徹也,田村和夫. 慣性質量ダンパーを組み込んだ構造物への地震入力エネルギーに関する研究[C]∥日本建築学会構造系論文集.Tokyo : Showa Joho Process Co., Ltd.,2010,75:751-759. [9] HIGASHINO S, KITAMURA H. Energy-balance based seismic response prediction methods for seismic isolated buildings with rubber bearings and viscous dampers[J].Journal of Structural and Construction Engineering,2010,75(588):79-86. [10] 佐藤大輔,北村春幸,佐藤大樹.履歴ダンパーと黏性ダンパーを併用した制振構造のエネルギーの釣合に基づく応答予測法[C]∥日本建築学会構造系論文集.東京:昭和情報プロセス株式会社,2014,79:631-640. [11] 裴星洙,王佩. 框架-摇摆墙结构阻尼优化设计方法研究[J]. 振动与冲击,2014,33(24):112-122. PEI Xingzhu, WANG Pei. Damping optimization design method of a frame-rocking wall structure[J]. Journal of Vibration and Shock, 2014, 33(24): 112-122. Optimizationdesignmethodfortunedviscousmassdampersbasedontheenergybalanceprinciple PEI Xingzhu1, QIU Jixiang2, FU Tiantian1 (1. School of Civil Engineering and Architecture,Jiangsu University of Science and Technology, Zhenjiang 212003, China;2. International Century Design of Architecture Co., Ltd., Changzhou 213000,China) A multi-layer steel frame structure equipped with tuned viscous mass dampers was designed and its mechanical models were proposed. The energy balance equation was established and the expressions for the elastic vibration energy of the structure and dampers as well as the energy dissipation of viscous dampers were presented. Prediction formulas for the shear coefficients and story drifts were derived.Simplified formulas for the energy dispersion coefficients of mass dampers and viscous dampers were put forward. A time history analysis validated the accuracy of the prediction and simplification. Optimized arrangements of dampers to meet different requirements were obtained according to the different linear combinations of displacement reduction rate and acceleration reduction rate. It is concluded: the simplified formulas can match well with the real energy dispersion coefficients and the prediction curves can envelope and match well with the results of the time history analysis. When the structure parameters reach an optimal condition, i.e., mass ratio 0.2,stiffness ratio 0.8 and dampers’ damping ratio 0.8, the structure seismic performance will be the best in various application conditions. tuned viscous mass damper; energy balance equation; prediction formula; simplified formula; energy dispersion coefficient; optimized arrangement TU352.1 A 10.13465/j.cnki.jvs.2017.19.005 江苏科技大学科研基金项目(1012920603) 2016-05-03 修改稿收到日期:2016-08-16 裴星洙 男,博士,教授,1954年10月生 邱吉祥 男,硕士生,1992年6月生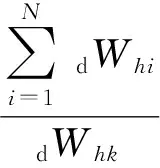
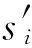
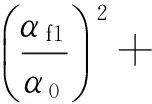
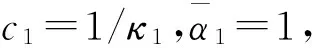
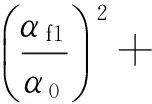
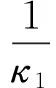
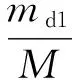
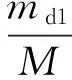
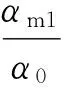
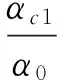
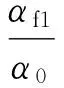
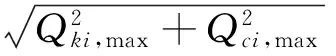
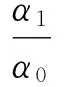
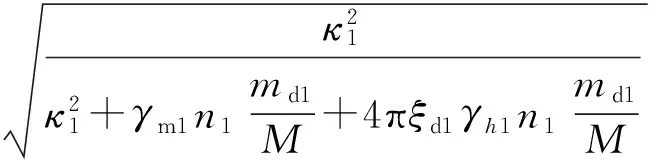
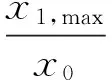
4 简化公式
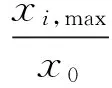
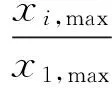
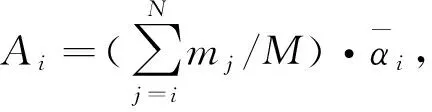
5 地震反应时程分析


6 阻尼量的确定

7 结 论
