基于非局部理论的轴向运动黏弹性纳米板的参数振动及其稳定性

刘金建，谢 锋，姚林泉，李 成

(苏州大学 城市轨道交通学院，江苏 苏州 215131)

基于非局部理论的轴向运动黏弹性纳米板的参数振动及其稳定性

刘金建，谢 锋，姚林泉，李 成

(苏州大学 城市轨道交通学院，江苏 苏州 215131)

研究了轴向运动黏弹性二维纳米板结构的非局部横向参数振动及其稳态响应。利用哈密顿原理推导了问题模型的控制方程，应用多尺度法分析了带有周期脉动成分的变速运动黏弹性纳米板的失稳现象。根据边界条件及复模态法可确定模态函数的表达，讨论了其特例匀速运动时固有频率与小尺度参数的关系，重点探讨了当脉动频率为两阶固有频率之和或者为某阶固有频率二倍时所发生的和型组合参数共振及主参数共振。结果表明，小尺度参数的存在使得轴向运动黏弹性纳米板的弯曲刚度及固有频率减小，并导致组合参数共振失稳区域减小但主参数共振区域增大，同时削弱了黏弹性系数对主参数共振区域的影响。同等条件下，黏弹性系数对组合共振区域的影响更为明显。

非局部弹性理论；轴向运动；黏弹性纳米板；多尺度法；参数稳定

轴向运动系统在航天航空、军事、电子、机械等领域有着广泛的应用，多种工程系统如带锯、缆绳等都可以模型化为轴向运动结构。目前，轴向运动弦、梁、板等宏观结构已经得到较为广泛的研究。比如Chen等[1]研究了扭力弹簧支撑的轴向运动梁的振动及其稳定性。Zhang等[2]研究了超临界区域内轴向运动黏弹性梁非线性受迫振动的周期稳态响应。Liu等[3]应用多尺度法讨论了轴向运动黏弹性梁在随机周期激励下的动态响应。胡宇达等[4]研究了磁场环境中轴向运动导电薄板的磁弹性振动问题。Marynowski等[5]利用扩展伽辽金法分析了热载荷作用下轴向运动板的动态性能。李成等[6]讨论了轴向运动超薄梁的非局部动力学性能。Sui等[8]基于Timoshenko梁理论探讨了轴向运动功能梯度梁的横向振动问题。Yang等[9]考察了轴向运动梁的纵、横向耦合非线性振动。Yan等[10]重点讨论外部谐波激励下轴向变速运动黏弹性Timoshenko梁的非线性动力学行为。基于黏弹性材料和变截面结构的工程前景，李成澄等[11]考察了轴向运动变截面黏弹性梁的振动与稳定性问题。

随着纳米时代的到来，碳纳米管、石墨烯等纳米结构引起了研究者的广泛兴趣。经典连续力学已被证实难以预测纳米材料固有的小尺寸效应，而Eringen等[12-13]提出的非局部理论能够有效的反映尺度因素的影响。因此，非局部理论在计及尺度效应的纳米力学研究中应用广泛。Murmu等[14]应用非局部理论分析了单向预应力条件下纳米板的振动。LI等[15]分析了轴向受变载荷作用下非局部纳米梁的横向振动响应及其稳定性。Shen等[16]基于基尔霍夫板理论分析了非局部单层石墨烯纳米传感器的振动响应。Thai[17]应用非局部理论研究了纳米梁的弯曲、屈曲及其振动响应。Liang等[18]建立了非局部应力模型以预测小尺度效应对石墨烯纳米板的影响。Fu等[19]基于精细非局部理论研究了核壳纳米线的非线性自由振动。确定纳米材料的动态响应及其稳定性，掌控纳米材料工作的可靠性是其应用和推广的必要前提。然而，在已有文献中，未见对轴向运动黏弹性纳米板的非局部动力学探讨。

本文从纳机电系统中的纳米传动带、随血液循环的纳米医学机器人的伸缩臂等纳米工程背景中提炼出轴向运动纳米板结构。基于非局部基尔霍夫板理论，以多尺度法和复模态法研究了带有周期脉动成分的轴向变速运动黏弹性纳米板的稳定性，重点分析了尺度参数对纳米动力系统主参数共振及组合参数共振失稳区域的影响。研究结论对二维纳米结构动力学及其控制具有一定的价值。

1 理论模型

经典连续力学认为，连续体内任一点的应力仅与该点处的应变有关。考虑到尺度效应及分子/原子间作用力的存在，非局部理论则认为在参考点处的非局部应力不仅取决于该点处的应变，还取决于体内其他所有点的应变。Eringen等提出的均质各向同性弹性体内的非局部微分本构方程为

(1)

考虑沿着x方向以速度v做轴向运动的矩形纳米板，其在x、y、z方向上的长度、宽度和厚度分别是la、lb、h。假设中面位移为0，根据经典板理论可知应变分量为

εxx=-zw,xx

εyy=-zw,yy

εxy=-2zw,xy

(2)

式中：t为时间；w为挠度。

本文考虑的黏弹性纳米板基于Kelvin-Voigt模型，其非局部本构关系为

(3)

式中，E、η和μ分别为杨氏模量、黏弹性系数和泊松比。

利用哈密顿原理推导问题的数学模型。首先，对形变能变分可得

(4)

其次，对外力功变分为

(5)

式中，FTx为沿着x方向的拉力。

最后，对动能变分得

(6)

式中，ρ为纳米板的质量密度。

根据哈密顿原理可得

(7)

将式(4)～式(6)代入式(7)推得轴向运动黏弹性纳米板的横向自由振动控制方程为

(8)

运用如下无量纲变量

W,TT+2γW,XT+(γ2-1)W,XX+γ,TW,X+[ζ-τ2(γ2-1)]W,XXXX+[2ζξ2-τ2ξ2(γ2-1)]W,XXYY+ζξ4W,YYYY-τ2[W,XXTT+2γW,XXXT+γ,TW,XXX+ξ2(W,YYTT+2γW,XYYT+γ,TW,XYY)]=-εα[W,XXXXT+2ξ2W,XXYYT+

ξ4W,YYYYT+γ(W,XXXXX+2ξ2W,XXXYY+ξ4W,XYYYY)]

(9)

假设轴向速度γ随时间T做简谐波动，其主要部分是平均速度γ0，因此γ可写成

γ=γ0+εγ1sinωT

(10)

应用多尺度法，式(10)的解可设为

W(X,Y,T;ε)=W0(X,Y,T0,T1)+

εW1(X,Y,T0,T1)+O(ε)

(11)

式中，T0=T和T1=εT分别为快尺度和慢尺度时间。

将式(10)和式(11)代入式(9)，并归并ε的同次幂项，推得匀速运动和变速运动黏弹性纳米板的控制方程分别为

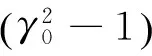
(12)

ζξ4W1,YYYY-τ2W1,XXT0T0-2τ2γ0W1,XXXT0-τ2ξ2W1,YYT0T0-2τ2ξ2γ0W1,XYYT0=

-2W0，T0T1-2γ0W0，XT1+2τ2γ0W0，XXXT1+2τ2W0，XXT0T1+2τ2ξ2γ0W0，XYYT1+

2τ2ξ2W0，YYT0T1+(2τ2γ0γ1W0，XXXX+2τ2ξ2γ0γ1W0，XXYY-2γ1W0，XT0-

2γ0γ1W0，XX+2τ2γ1W0，XXXT0+2τ2ξ2γ1W0，XYYT0)sinωt+(τ2ωγ1W0，XXX+

τ2ξ2ωγ1W0，XYY-ωγ1W0，X)cosωt-α[W0,XXXXT0+2ξ2W0,XXYYT0+ξ4W0,YYYYT0+

γ0(W0,XXXXX+2ξ2W0,XXXYY+ξ4W0,XYYYY)]

(13)

设方程式(12)的解为

(14)

式中：ψmn、ωmn分别为第mn阶模态函数和固有频率；cc为等式右端之前各项的共轭复数。

将式(14)代入式(12)推得

(15)

根据分离变量思想，方程式(15)的解可设为

ψmn=φm(X)φn(Y)

(16)

2 算例分析与讨论

为了具体讨论小尺度参数对轴向运动黏弹性纳米板横向振动的影响，分别考虑四边简支和四边固支两类纳米板的边界条件。Tang等和Murmu等分别探讨了轴向运动黏弹性和非局部理论对边界约束条件的影响，四边简支和四边固支的数学表达式可简化为

(17)

(18)

2.1模态函数的确定及匀速运动稳定性分析

2.1.1 四边简支情形

根据边界条件式(17)，可设四边简支轴向运动纳米板沿Y方向的振型函数为

φn=sin(nπY)

(19)

将式(19)代入式(15)可得

[2γ0iωmn+2τ2n2π2ξ2γ0iωmn]φm,X+

(20)

常微分方程式(20)的解可设为

φm(X)=C1m(eiβ1mX+C2meiβ2mX+

C3meiβ3mX+C4meiβ4mX)

(21)

将式(21)代入式(20)推得

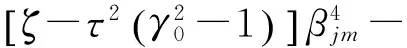
[2γ0ωmn+2τ2n2π2ξ2γ0ωmn]βjm+

(22)

式中，j=1,2,3,4。根据式(21)及式(17)中X方向上的边界条件，可解得第m阶模态函数。进一步将式(21)代入边界条件式(17)，并令所得结果的系数行列式为0，可确定βjm及匀速运动情况下第mn阶固有频率ωmn。

2.1.2 四边固支情形

根据式(18)可知，四边固支运动纳米板沿Y方向的振型函数可设为

φn= [coshβnY-cosβnY+

(23)

式中，cosβncoshβn=1。

将式(23)代入式(15)并对Y积分推得

[2γ0iωmn-2κτ2ξ2γ0iωmn]φm,X+

(24)

同样设式(21)是方程式(24)的解，并将其代入式(24)得

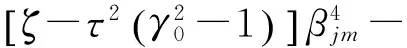
[2γ0ωmn-2κτ2ξ2γ0ωmn]βjm+

(25)

根据同样的分析思路，可求得四边固支条件下的四个未知特征根βjm及固有频率ωmn。

2.2变速运动时参数共振稳定性分析

应用式(13)可以分析带有周期脉动成分变速运动黏弹性纳米板的参数稳定性。当速度的脉动频率ω接近某阶固有频率两倍或者为某两阶频率之和时将发生共振现象。

2.2.1 和式组合参数共振

当脉动频率为两阶固有频率之和时，系统将发生和式组合共振。现引入调谐参数σ表示脉动频率ω在ωkl+ωk′l′附近变化

ω=ωkl+ωk′l′+εσ

(26)

式中，ωkl、ωk′l′分别为系统的第kl、k′l′阶频率。为分析和式组合共振响应，方程式(12)的解可设为

W0(X,Y,T0,T1)=ψkl(X,Y)Akl(T1)eiωklT0+

ψk′l′(X,Y)Ak′l′(T1)eiωk′l′T0+cc

(27)

将式(26)和式(27)代入式(13)，并把右端的三角函数转换为指数形式可得

ζξ4W1,YYYY-τ2W1,XXT0T0-2τ2γ0W1,XXXT0-τ2ξ2W1,YYT0T0-2τ2ξ2γ0W1,XYYT0=

{(-2iωklψkl-2γ0ψkl,X+2τ2γ0ψkl,XXX+2τ2iωklψkl,XX+2τ2ξ2γ0ψkl,XYY+2τ2ξ2iωklψkl,YY)Akl,T1+

2ξ2ψkl,XXXYY+ξ4ψkl,YYYYY)]Akl}eiωklT0+

{(-2iωk′l′ψk′l′-2γ0ψk′l′,X+2τ2γ0ψk′l′,XXX+2τ2iωk′l′ψk′l′,XX+2τ2ξ2γ0ψk′l′,XYY+2τ2ξ2iωk′l′ψk′l′,YY)Ak′l′,T1+

2ξ2ψk′l′,XXXYY+ξ4ψk′l′,YYYYY)]Ak′l′}eiωk′l′T0+cc+NST

(28)

式中，NST为不会给解带来长期项的所有项。若要使得解不存在长期项则非齐次微分方程式(28)的非齐次部分与其伴随方程的其次解正交，即有如下的正交关系

〈(-2iωklψkl-2γ0ψkl,X+2τ2γ0ψkl,XXX+2τ2iωklψkl,XX+2τ2ξ2γ0ψkl,XYY+2τ2ξ2iωklψkl,YY)Akl,T1+

2ξ2ψkl,XXXYY+ξ4ψkl,YYYYY)]Akl，ψkl〉=0

(29a)

〈(-2iωk′l′ψk′l′-2γ0ψk′l′,X+2τ2γ0ψk′l′,XXX+2τ2iωk′l′ψk′l′,XX+2τ2ξ2γ0ψk′l′,XYY+2τ2ξ2iωk′l′ψk′l′,YY)Ak′l′,T1+

2ξ2ψk′l′,XXXYY+ξ4ψk′l′,YYYYY)]Ak′l′，ψk′l′〉=0

(29b)

其中，复方程在区间[0,1]上的内积为

(30)

于是由式(29)推得

(31a)

(31b)

可见式(32)的结果仅仅由模态函数所决定，而与轴向速度脉动量无关。

现做如下变换

(32)

把式(32)代入式(31)推得

(33)

方程式(33)有零解，通过分析其非零解情况，可推得和式组合参数共振失稳区域的边界为

(34)

式中：上标R为实部；I为虚部。

2.2.2 主参数共振

当速度的脉动频率接近某阶固有频率的两倍时，系统将发生主参数共振，同样引入调谐参数σ，那么脉动频率ω可表示为

ω=2ωkl+εσ

(35)

此时，式(12)的解可设为

W0(X,Y,T0,T1)=ψkl(X,Y)Akl(T1)eiωklT0+cc

(36)

将式(35)和式(36)代入式(13)推得

(37)

其中,

(38a)

(38b)

作如下变换

Akl(T1)=Bkl(T1)e0.5iσT1

(39)

将式(39)代入式(37)推得

(40)

将式(40)的解分为实部和虚部则有

Bkl=p(T1)+iq(T1)

(41)

式中，p、q为与时间T1有关的实数。将式(41)代入式(40)并将结果分离成实部和虚部推得

p,T1=-[αdkl+γ1Re(ckl)]p+

[0.5σ-γ1lm(ckl)]q

q,T1=-[0.5σ+γ1lm(ckl)]p-

[αdkl-γ1Re(ckl)]q

(42)

式(42)的特征方程为

(43)

根据Routh-Hurwitz稳定判据求得式(43)的稳定区域为

(44)

在以下数值计算中，取参考文献[16]中的数据进行计算，即纳米板的杨氏模量E=1.06 TPa，泊松比μ=0.25，质量密度ρ=225 kg/m3，厚度h=0.34 nm，长度la=20 nm，宽度lb=20 nm。四边简支纳米板前四阶频率ωmn随着小尺度参数τ的变化见图1，其中平均速度γ0=2、长宽比ξ=1、刚度比ζ=1。由图1可以看出，当τ=0时，ωmn取得最大值即非局部效应的存在使得简支纳米板的等效刚度减小，从而导致ωmn随之减小，且非局部效应越大ωmn的减幅越大。进一步发现，当τ很小时(1,2)阶频率ω12和(2,1)阶频率ω21相当接近，但随着尺度效应的增强，其结果区别明显。

图2(a)和图2(b)分别给出了当τ=0.001、τ=0.05、τ=0.1时四边简支第一阶和第二阶以及第三阶和第四阶组合参数共振在σ-γ1平面上的失稳区域，其中α=0.000 1、γ0=2、ξ=1、ζ=1。由图2知组合参数共振失稳区域随着τ即非局部效应的增大而减小，即在给定σ值时，非局部效应越大对应的脉动振幅γ1越大；反之当给定γ1时，失稳范围随着非局部效应的增大而减小。同时由图2可见抛物线的最低点对应的γ1值随着非局部效应的增大而增大，因此黏弹性系数对组合稳定区域的影响随着非局部效应的增大而越发明显。图3(a)～图3(d)分别给出了四边简支前四阶主参数共振的失稳区域。对比图2和图3发现，主参数共振与组合参数共振的不同之处在于，随着小尺度参数的增大失稳区域亦随之增大。考虑到图3中抛物线最低点对应的γ1值随着非局部效应的增大而减小，因此非局部效应的存在削弱了黏弹性系数对主参数共振失稳区域的影响。

图1 四边简支条件下前四阶固有频率随着小尺度参数的变化
Fig.1 Effects of small-scale parameter on the first four frequencies for simply supported case

(a) 第一阶和第二阶组合参数共振

(b) 第三阶和第四阶组合参数共振图2 小尺度参数对四边简支条件下组合参数共振边界的影响Fig.2 Effects of small-scale parameter on the boundaries of summation parametric resonance for simply supported case

图4给出了四边固支轴向运动黏弹性纳米板前四阶频率随着非局部效应的变化，其中γ0=2、ξ=1、ζ=1。ωmn随着小尺度参数的变化趋势与简支的情形一致。同等条件下，固支纳米板的横向振动频率大于简支纳米板。

选取与上述简支纳米板相同的参数，下面讨论固支条件下的组合共振及主参数共振。图5(a)～图5(b)分别作出了当τ=0.001、τ=0.05、τ=0.1时四边固支变速运动黏弹性纳米板第一阶和第二阶，以及第三阶和第四阶组合参数共振的失稳区域，图6(a)～图6(d)分别给出了固支条件下前四阶主参数共振的失稳区域。由图5和图6发现固支纳米板组合参数共振与主参数共振失稳区域随着τ及α的变化规律与简支纳米板的定性结论是一致的。

(a) 第一阶主参数共振

(b) 第二阶主参数共振

(c) 第三阶主参数共振

(d) 第四阶主参数共振图3 小尺度参数对四边简支条件下主参数共振边界的影响Fig.3 Effects of small-scale parameter on boundaries of the principal parametric resonance for simply supported case

图4 四边固支条件下前四阶频率随着小尺度参数的变化Fig.4 Effects of small-scale parameter on the first four frequencies for fully clamped case

以上分析了小尺度参数对固有频率和参数共振的影响，下面再分析轴向运动速度对纳米板前两阶固有频率的影响，如图7所示，其中小尺度参数τ=0.02、长宽比ξ=1、刚度比ζ=1。注意横坐标即无量纲轴向速度的选取是基于人体血液循环速度，一般情况下，动脉约为0.50 m/s，静脉约为0.2 m/s，毛细血管约为0.01～0.02 m/s。由图7可以看出，轴向运动纳米板的固有频率随着速度的增大而减小，这是因为轴向运动速度的存在削弱了纳米结构的刚度，进而降低了振动频率，在已有的轴向运动宏观结构的研究中，同样证明了这一点。因此，在实际工程应用中，比如针对纳米医学机器人，必须考虑血液循环速度带来的影响。

(a) 第一阶和第二阶组合参数共振

(b) 第三阶和第四阶组合参数共振图5 小尺度参数对四边固支条件下组合参数共振边界的影响Fig.5 Effects of small-scale parameter on boundaries of the summation parametric resonance for fully clamped case

(a) 第一阶主参数共振

(b) 第二阶主参数共振

(c) 第三阶主参数共振

(d) 第四阶主参数共振图6 小尺度参数对四边固支条件下主参数共振边界的影响Fig.6 Effects of small-scale parameter on boundaries of the principal parametric resonance for fully clamped case

图7 纳米板前二阶固有频率随着速度的变化Fig.7 Effects of axial velocity on the first two frequencies for nanoplates

3 结 论

基于Eringen非局部弹性理论分析了轴向运动黏弹性纳米板的横向振动响应及其稳定性，讨论了各主要参数对横向振动及失稳区域的影响。结论如下：

(1) 小尺度参数的存在降低了轴向运动黏弹性纳米板的刚度，从而导致横向振动频率随着非局部效应的增大而减小，且非局部效应越大其减小的幅度越大。同等条件下，四边固支轴向运动黏弹性纳米板的横向振动频率大于四边简支情形。

(2) 组合参数共振失稳区域随着非局部效应的增大而减小，而主参数共振失稳区域却随之增大。小尺度参数的存在削弱了黏弹性系数对主参数共振失稳区域的影响，却增强了黏弹性系数对组合参数共振的影响。

(3) 轴向运动速度对纳米板的振动频率影响显著，轴向速度越大，振动固有频率越低，这一点与轴向运动宏观结构的结论是一致的。

[1] CHEN L Q, YANG X D. Vibration and stability of an axially moving viscoelastic beam with hybrid supports[J]. European Journal of Mechanics-A/Solids, 2006, 25(6): 996-1008.

[2] ZHANG G C, DING H, CHEN L Q, et al. Galerkin method for steady-state response of nonlinear forced vibration of axially moving beams at supercritical speeds[J]. Journal of Sound and Vibration, 2012, 331(7): 1612-1623.

[3] LIU D, XU W, XU Y. Dynamic responses of axially moving viscoelastic beam under a randomly disordered periodic excitation[J]. Journal of Sound and Vibration, 2012, 331(17): 4045-4056.

[4] 胡宇达, 孙建涛, 杜国君. 轴向运动导电薄板的磁弹性振动[J]. 振动与冲击, 2013, 32(13): 34-38.

HU Yuda, SUN Jiantao, DU Guojun. Magneto-elastic vibration of an axially moving current-conducting thin plate[J]. Journal of Vibration and Shock, 2013, 32(13): 34-38.

[5] MARYNOWSKI K, GRABSKI J. Dynamic analysis of an axially moving plate subjected to thermal loading[J]. Mechanics Research Communications, 2013, 51(3): 67-71.

[6] 李成, 姚林泉. 轴向运动超薄梁的非局部动力学分析[J]. 工程力学, 2013, 30(4): 366-372.

LI Cheng, YAO Linquan. Nonlocal dynamical analysis on axially travelling ultra-thin beams[J]. Engineering Mechanics, 2013, 30(4): 366-372.

[7] TANG Y Q, CHEN L Q. Stability analysis and numerical confirmation in parametric resonance of axially moving viscoelastic plates with time-dependent speed[J]. European Journal of Mechanics-A/Solids, 2013, 37(37): 106-121.

[8] SUI S H, CHEN L, LI C, et al. Transverse vibration of axially moving functionally graded materials based on Timoshenko beam theory[EB/OL]. (2014-08-16)[2014-10-18].http://dx.doi.org/10.1155/2015/391452.

[9] YANG X D, ZHANG W. Nonlinear dynamics of axially moving beam with coupled longitudinal-transversal vibrations[J]. Nonlinear Dynamics, 2014, 78(4): 2547-2556.

[10] YAN Q, DING H, CHEN L Q. Nonlinear dynamics of axially moving viscoelastic Timoshenko beam under parametric and external excitations[J]. Applied Mathematics and Mechanics, 2015, 36(8): 971-984.

[11] 李成澄, 赵凤群. 轴向运动变截面黏弹性梁的振动与稳定性分析[J].振动与冲击, 2016, 35(14): 107-111.

LI Chengcheng, ZHAO Fengqun.Vibration and stability analysis of axially moving viscoelastic beam with varying section[J]. Journal of Vibration and Shock, 2016, 35(14): 107-111.

[12] ERINGEN A C, EDELEN D G B. On nonlocal elasticity[J]. International Journal of Engineering Science, 1972, 10(3): 233-248.

[13] ERINGEN A C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves[J]. Journal of Applied Physics, 1983, 54(9): 4703-4710.

[14] MURMU T, PRADHAN S C. Vibration analysis of nanoplates under uniaxial prestressed conditions via nonlocal elasticity[J]. Journal of Applied Physics, 2009, 106(10): 104301.

[15] LI C, LIM C W, YU J L. Dynamics and stability of transverse vibrations of nonlocal nanobeams with a variable axial load[J]. Smart Materials and Structures, 2011, 20(1): 015023.

[16] SHEN Z B, TANG H L, LI D K, et al. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory[J]. Computational Materials Science, 2012, 61(4): 200-205.

[17] THAI H T. A nonlocal beam theory for bending, buckling, and vibration of nanobeams[J]. International Journal of Engineering Science, 2012, 52(3): 56-64.

[18] LIANG Y, HAN Q. Prediction of the nonlocal scaling parameter for graphene sheet[J]. European Journal of Mechanics-A/Solids, 2014, 45(2): 153-160.

[19] FU Y, ZHONG J. Nonlinear free vibration of core-shell nanowires with weak interfaces based on a refined nonlocal theory[J]. Acta Mechanica, 2015, 226(5): 1369-1377.

Parametricvibrationandstabilityofanaxiallymovingviscoelasticnanoplatebasedonthenonlocaltheory

LIU Jinjian, XIE Feng, YAO Linquan, LI Cheng

(School of Urban Rail Transportation, Soochow University, Suzhou 215131, China)

The nonlocal transverse parametric vibration and steady-state response of axially moving viscoelastic two-dimensional nanoplate-like structures were concerned. The Hamilton’s principle was employed to derive the governing partial differential equations of the mathematical model. The instable behaviors of an axially moving viscoelastic nanoplate with some periodic pulsation velocity were addressed using the method of multiple scales. The modal functions were determined under some specific boundary conditions by using the method of complex mode. The effects of small-scale parameters on the natural frequencies of the axially moving nanoplate with uniform velocity were discussed. Subsequently, the analyses were mainly focused on the instable regions caused by the summation parametric resonance and principal parametric resonance respectively. The summation parametric resonance occurs when the pulsation frequency approaches the sum of any two modal frequencies, while the principal parametric resonance occurs when the frequency approaches two times the natural frequency of certain mode. It is shown that the existence of small-scale parameter contributes to reduce the bending stiffness and natural frequencies of axially moving viscoelastic nanoplates, and further decreases the instable regions of the summation parametric resonance, while increases the instable regions of the principal parametric resonance. On the other hand, the small-scale parameter softens the influence of viscoelasticity on the instable regions of the principal parameter resonance. Moreover, the effect of viscoelasticity on the instability of the summation parametric resonance is more obvious, ceteris paribus.

nonlocal elasticity theory; axially moving; viscoelasticity nanoplate; method of multiple scales; parameter stability

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.19.003

国家自然科学基金(11572210)；江苏省自然科学基金(BK20130303)；苏州市科技计划项目(SYG201537)；苏州大学“东吴学者”计划项目(R513300116)

2016-04-27 修改稿收到日期：2016-08-01

刘金建 男，硕士生，1989年生

李成 男，博士，副教授，硕士生导师，1983年生