狙击步枪弹/枪相互作用数值研究

刘国庆，徐 诚，丁传俊

(南京理工大学 机械工程学院，南京 210094)

狙击步枪弹/枪相互作用数值研究

刘国庆，徐 诚，丁传俊

(南京理工大学 机械工程学院，南京 210094)

为深入研究弹头膛内发射过程，基于非线性有限元理论建立了弹/枪相互作用数值计算模型。模型将内弹道计算与弹头发射过程有限元计算相耦合，真实地反映了膛压生成与弹头膛内运动之间的耦合关系；模型考虑了弹头挤进过程，将挤进过程与后续内弹道过程相结合，保持了内弹道过程的完整性；模型考虑了枪管在重力作用下的预弯曲现象，是一个较为完善的求解弹头发射过程理论模型；通过对比试验结果与仿真结果证明了模型的正确性。借助该模型对弹头膛内发射过程进行了数值计算，获得了弹头受力、应力/应变分布、有无重力作用下的枪口振动情况与弹头膛内摆动情况，揭示了弹/枪相互作用机理。

狙击步枪；相互作用；数值模型；挤进过程；耦合计算；重力作用

弹头膛内发射过程即弹/枪相互作用过程，是一个具有瞬时特性的高度非线性问题，涉及多种物理场的耦合、材料大应变塑性行为、复杂的接触-摩擦及弹头周期性摆动等方面，难以建立求解方程获得所有问题的解析解，需要采用数值计算的方法进行求解[1-2]。

近年来随着求解策略的完善，材料模型及边界条件等的可开发性提高，有限元法已广泛应用于求解弹头发射中各种复杂的非线性动力学问题，但目前所建立的弹头发射过程计算模型往往是不完善的。如林秉奇[3]采用弹/炮耦合有限元模型研究了某大口径牵引火炮的动态发射特性，分析了重力作用下弹头不均衡因素、前后衬瓦间隙及高平机等效刚度对炮口扰动等的影响，但忽略了弹头挤进过程，弹头本体也进行了刚化处理，不能反映挤进过程对弹/炮相互作用状态的影响；顾玮等[4-5]建立了火炮弹头挤进过程有限元计算模型，将内弹道膛压计算与挤进过程有限元计算相耦合，开辟了一种全新的挤进过程研究方法，然而并未对后续内弹道过程进行探讨；South等[6]建立了M855型步枪弹的发射过程有限元模型，模拟软质弹头与枪管的相互作用过程，揭示了弹头壳与铅质弹芯材料流动及其动力学特性，但模型并未考虑重力作用导致的枪管弯曲现象。

目前针对弹头发射过程的数值计算模型研究主要针对火炮或普通枪械，狙击步枪在弹头结构、枪管结构方面与火炮或普通枪械具有较大的不同，不宜将研究成果应用于狙击步枪；现有的计算模型往往没有全面考虑重力对枪管的弯曲作用、弹头挤进过程、内弹道与弹头发射过程的耦合作用，不能准确的反映弹头-身管相互作用关系，因此本文以某型狙击步枪为研究对象，建立了一个较为完善的弹/枪相互作用有限元数值计算模型，综合考虑上述三个方面，求解弹头发射过程，揭示弹/枪相互作用机理。

1 弹/枪相互作用有限元数值计算模型

1.1三维建模及网格划分

依据枪管、狙击弹结构参数分别建立三维模型，使用有限元前处理软件划分网格，其网格模型如图1和图2所示。网格类型以六面体缩减积分线性实体单元为主(C3D8R)，其中枪管共划分267 529个网格，弹头壳共划分175 769个网格，铅芯共划分110 868个网格。

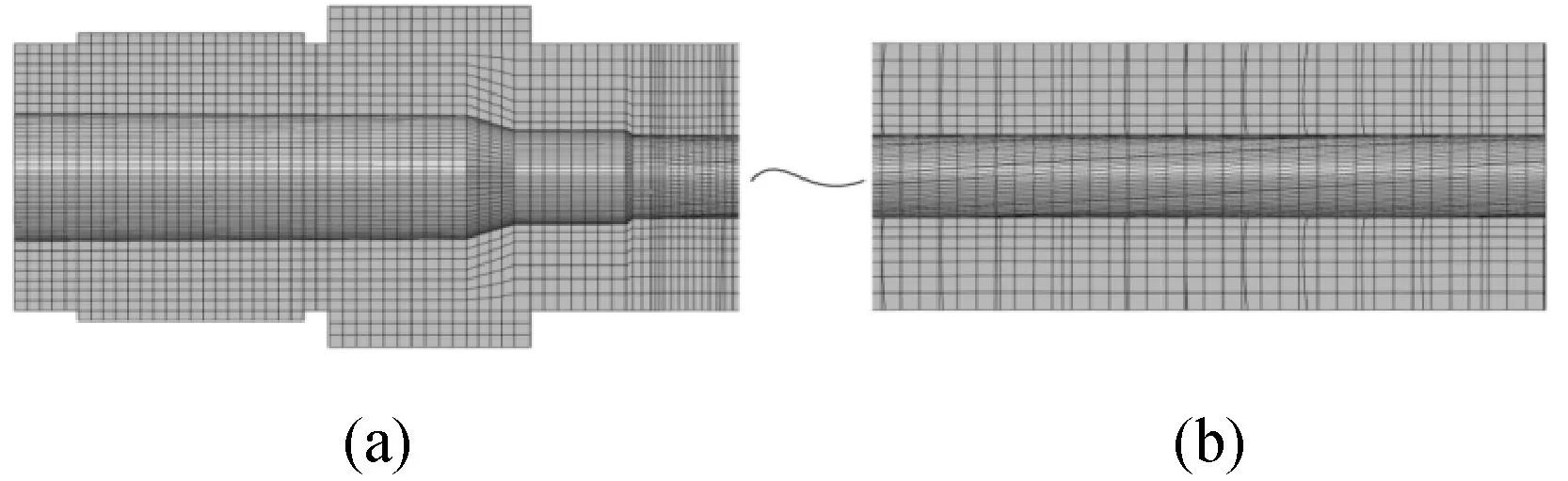
图1 枪管半剖网格模型Fig.1 Half sectional mesh model of sniper rifle

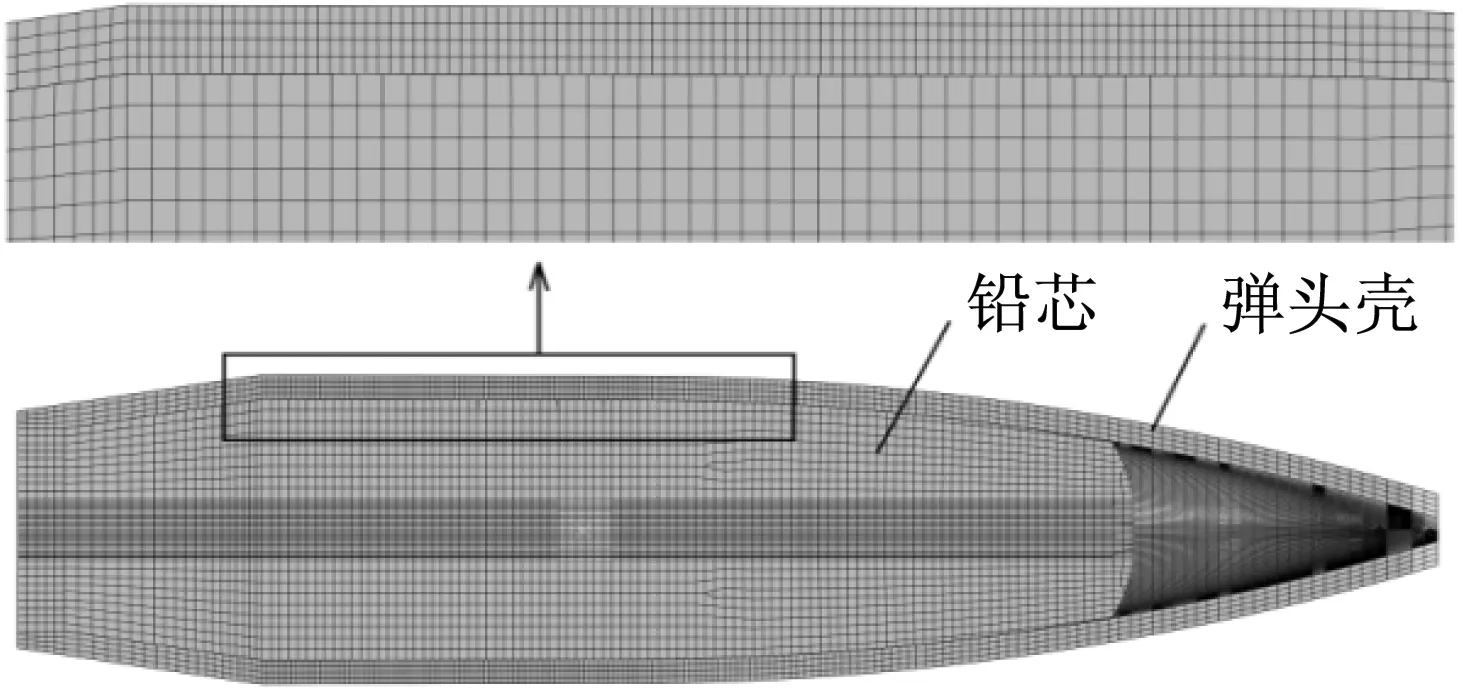
图2 弹头半剖网格模型Fig.2 Half sectional mesh model of bullet

1.2材料模型与摩擦因数

枪管为高强度钢，不考虑塑性变形仅赋予弹性属性；弹头壳为H90铜，芯部材料为纯铅，在挤进时发生弹塑性变形，且应变率较高，因此采用Johnson-Cook(J-C)模型定义材料属性，J-C模型形式简单，物理解释清楚，非常适合描述力学性能与应变率相关的金属，其本构模型如式(1)和式(2)所示

(1)

(2)

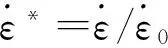
近代摩擦学研究认为，摩擦因数与接触面之间的压力、速度有关。1976年Montgomery设计的销-磨盘摩擦磨损试验证明金属试件与钢盘之间的摩擦因数随压力与速度乘积的增大而减小；周彦煌[7]采用拟合法给出了摩擦因数关于相对速度与压力乘积的分段函数，对于狙击步枪而言，弹头与枪管间的动摩擦因数应不大于0.02。

1.3接触属性与边界条件的设置

采用“面-面”接触类型定义弹头壳外表面与枪管内膛之间、弹头壳内表面与铅芯表面之间的接触，接触从初始步(Initial)即开始作用；接触控制算法采用罚函数法，其原理为当从面节点穿透主面时，求解器在节点上施加一个反作用力将其拉回到主面之上，阻力的大小与穿透量成正比关系，从而能够有效避免从面节点对主面的穿透。枪管通过螺纹联接的形式固定，因此约束枪管螺纹部的全部自由度模拟约束状态。

1.4连接器的使用及显隐式混合运算

ABAQUS的连接器功能可模拟多种形式的连接行为，本文分别在坐标原点、弹头质心处建立参考点及其附属坐标系，使用Cartesian与Euler相结合的方式连接坐标原点与弹头质心，两点之间无自由度约束，弹头质心与质心处少数单元设置刚体约束，从而可获得弹头质心在膛内运动时期的位移与转动情况。

模型考虑了重力作用导致的枪管预弯曲现象，在处理该问题时首先使用隐式求解器获得枪管在重力作用下的应力应变状态，而后将隐式计算结果导入显式求解器，重新设置约束状态、接触性质与初始场等计算初始条件，求解弹头发射过程，经混合运算获得重力对弹头膛内发射过程的影响。

1.5内弹道计算与ABAQUS数值计算耦合的实现

基于经典内弹道方程组，使用Fortran语言编写了内弹道计算程序，以四阶龙格库塔法求解内弹道微分方程组。耦合计算时，首先赋予ABAQUS初始膛压值，求解弹头速度与位移，然后由ABAQUS程序传感器将位移值、速度值等导入内弹道计算程序中，内弹道计算程序依据位移值与速度值求解新膛压值，新膛压值通过VUAMP加载于弹头，由ABAQUS再次求解位移与速度值，重复上述步骤直至弹头飞离枪管，耦合计算流程图如图3所示。

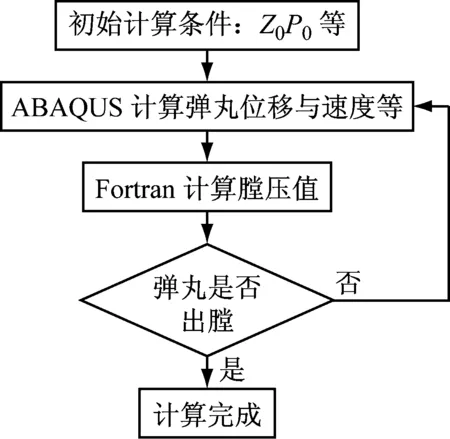
图3 耦合计算流程图Fig.3 The flow chart of coupling calculation

2 模型的验证

2.1膛压与初速

该型狙击步枪初速试验值为794 m/s，最大膛压试验值为302.6 MPa。经耦合计算所得膛压与初速随时间的变化趋势如图4所示。内弹道时期共持续了1.7 ms，膛压在0.78 ms时上升至最大值299.5 MPa，弹头初速值为792.8 m/s，最大膛压值与膛压实测试验值之间的误差约为1%，初速值与初速试验值之间的误差为0.15%，证明了弹/枪相互作用数值计算模型求解弹头膛内发射过程的正确性与有效性。弹头在0.6 ms时完成挤进，挤进完成时膛压为225.1 MPa，速度为96.8 m/s，挤进用时约占整个内弹道时期的1/3。

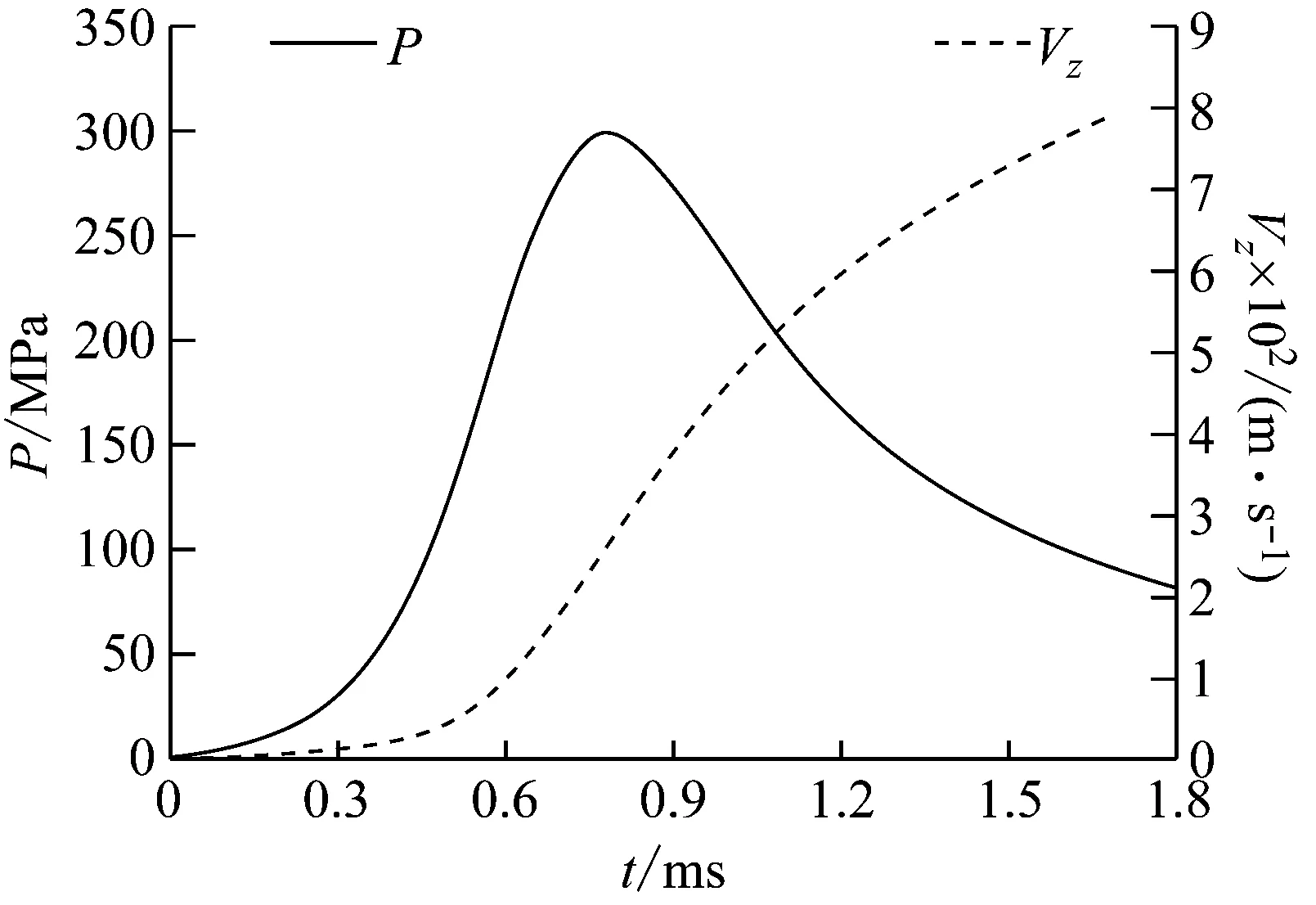
图4 膛压与速度曲线Fig.4 The curve of velocity and bore pressure

2.2枪口振动

(a) 枪口振动测试试验

采用高速摄影法获取弹头开始运动500 ms之内的枪口振动位移，高速摄影系统如图5所示，由高速摄影机、光源与PC机组成。高速摄像机拍摄速度为5 000帧/秒，拍摄照片像素大小为704×304。

图5 高速摄影系统Fig.5 High-speed photography system

图6所示枪口平均振动频率约为42 Hz，最大振动位移为1.02 mm，振动位移随时间增长而逐渐衰减；Y轴、Z轴分别为竖直方向、轴向，X轴由右手定则确定。

(b) 枪口振动数值计算

采用弹/枪相互作用数值模型求解枪口振动，枪口振动数值计算共分为三步:第一步为静平衡计算，即计算重力作用下发射系统的静平衡状态；第二步为弹头发射过程计算，将第一步计算所得各部件应力应变结果导入第二步计算作为初始条件，再次设置接触、约束等边界条件，计算弹头发射过程；第三步为弹头发射之后枪口振动计算，弹头发射完成后，除弹头之外的部件内应力应变结果导入第三步进行计算，最终获得枪口振动位移。其中第一步计算采用ABAQUS-Standard求解器，第二、三步计算采用ABAQUS-Explicit求解器进行求解。

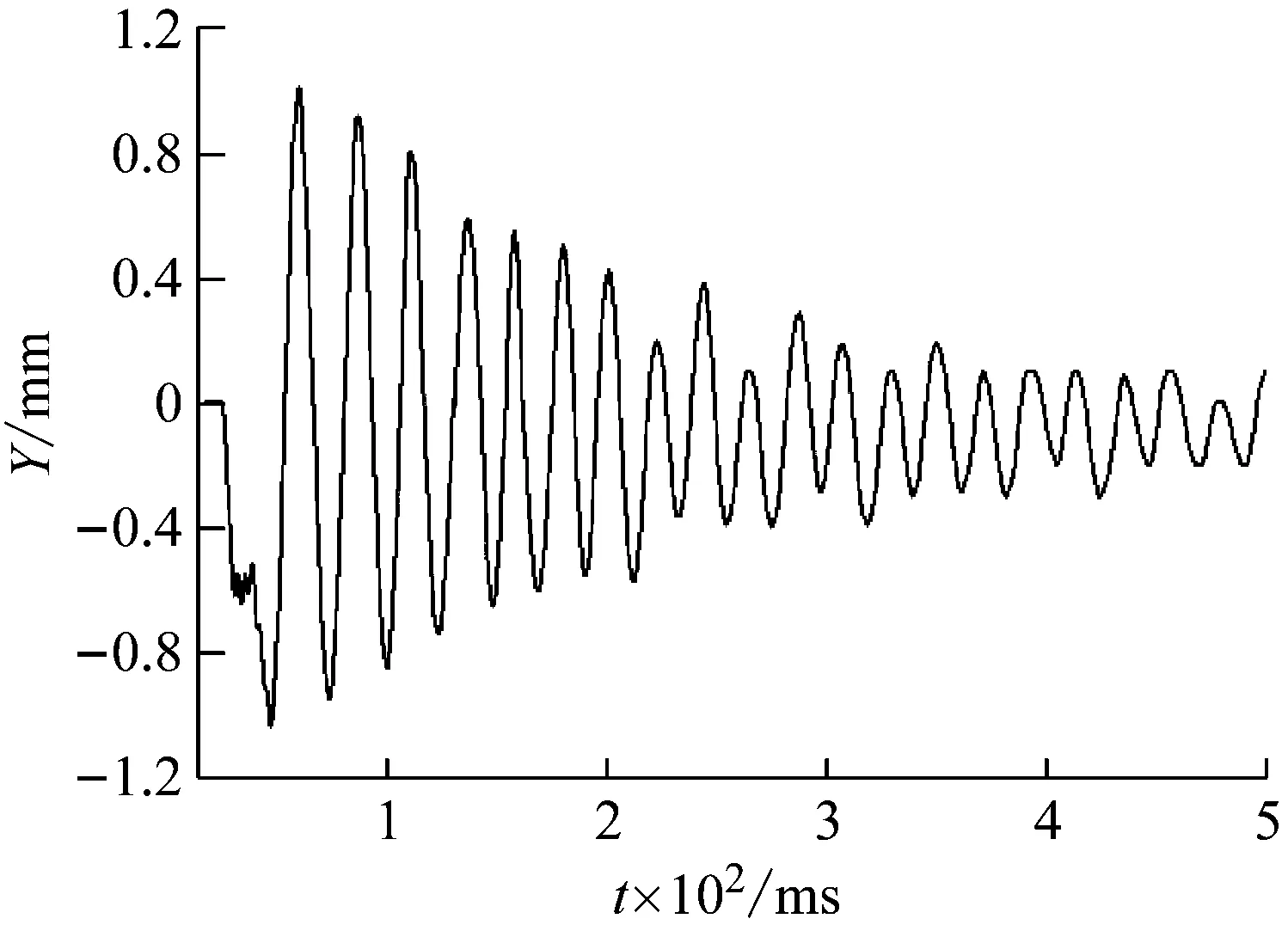
图6 枪口Y方向振动位移Fig.6 Vibration displacement of muzzle in Y-direction

依照计算顺序所得枪口振动位移曲线如图7所示，枪口振动计算结果衰减平缓，平均振动频率约为40 Hz，最大振动位移为0.997 mm。

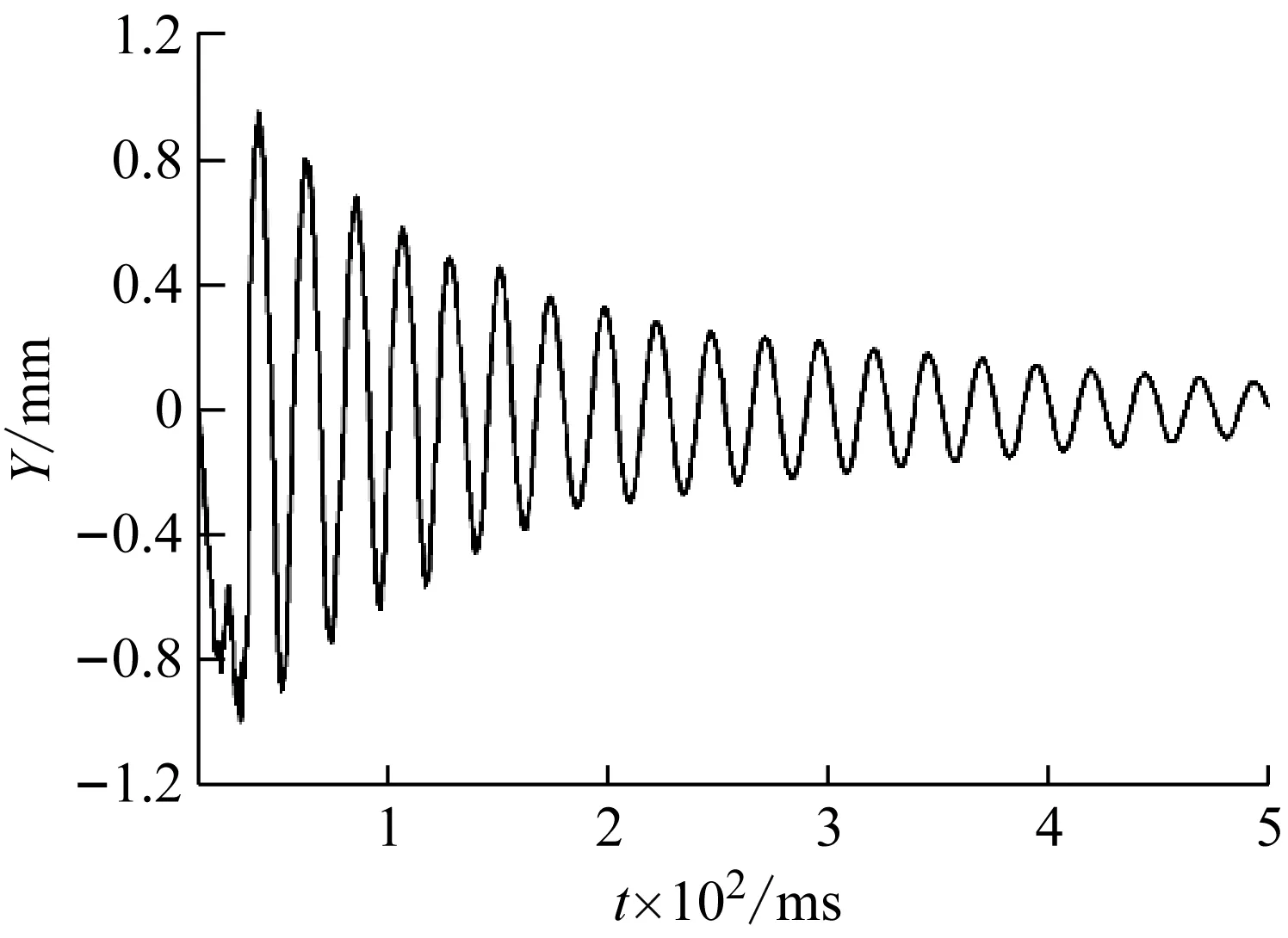
图7 枪口振动位移数值计算结果Fig.7 Results of numerical calculation of muzzle vibration

(c) 试验结果与数值计算结果对比

与试验结果相比，数值计算所得枪管振动频率值比试验值低4.76%，枪口振动最大幅值比试验值低2.25%；枪口振动波峰(谷)值试验结果与数值计算结果对比如图8所示。

枪口振动波峰(谷)试验结果与数值计算结果总体上较为符合，振动位移试验结果与数值计算结果平均误差0.09 mm，约占最大幅值的8.82%；振动衰减通常以衰减系数η表示，如式(3)所示，其中η为相邻两波峰(谷)的比值。枪口振动试验结果的平均衰减系数为1.132，数值计算结果平均衰减系数为1.136，二者较为接近，进一步证明弹/枪相互作用模型求解弹头膛内发射过程正确性。

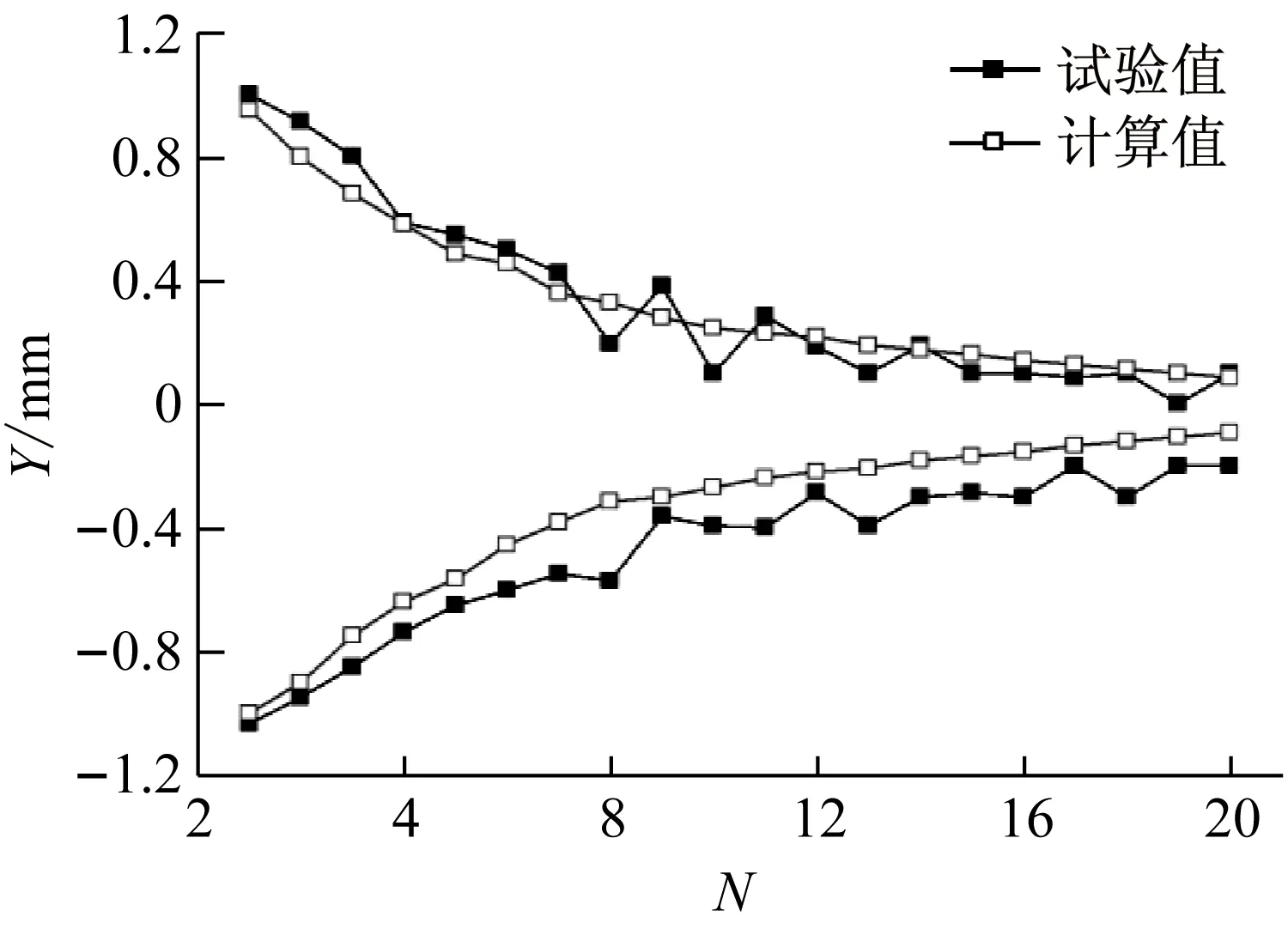
图8 试验结果与计算结果对比Fig.8 Comparison between experiment result and calculation result

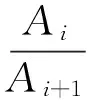
(3)

枪口振动能量主要来自于弹/枪相互作用过程中弹头对枪管的激励，弹头离膛后枪管振动能量积累至最大；在初始振动阶段，枪口振动能量大、衰减平稳，但随着振动能量的降低，枪口振动抗干扰能力下降，表现为振动衰减平稳性降低，如图8中试验结果第8个波峰(谷)之后的振动波峰(谷)值波动情况所示。

3 弹头膛内动力学机理研究

弹头发射过程是一个高度非线性动力学问题，主要涉及弹头受力、应力/应变分布及运动三个方面的内容。本节采用弹/枪相互作用数值计算模型对弹头膛内动力学过程的三个主要方面进行分析，并着重分析重力作用对枪口振动与弹头膛内运动方面的影响。

3.1弹头膛内轴向阻力分析

弹头在膛内轴向阻力如图9所示，其中FN为轴向正压力，FS为轴向摩擦力，F为二者合力即轴向阻力，弹头在0.6 ms完成挤进。

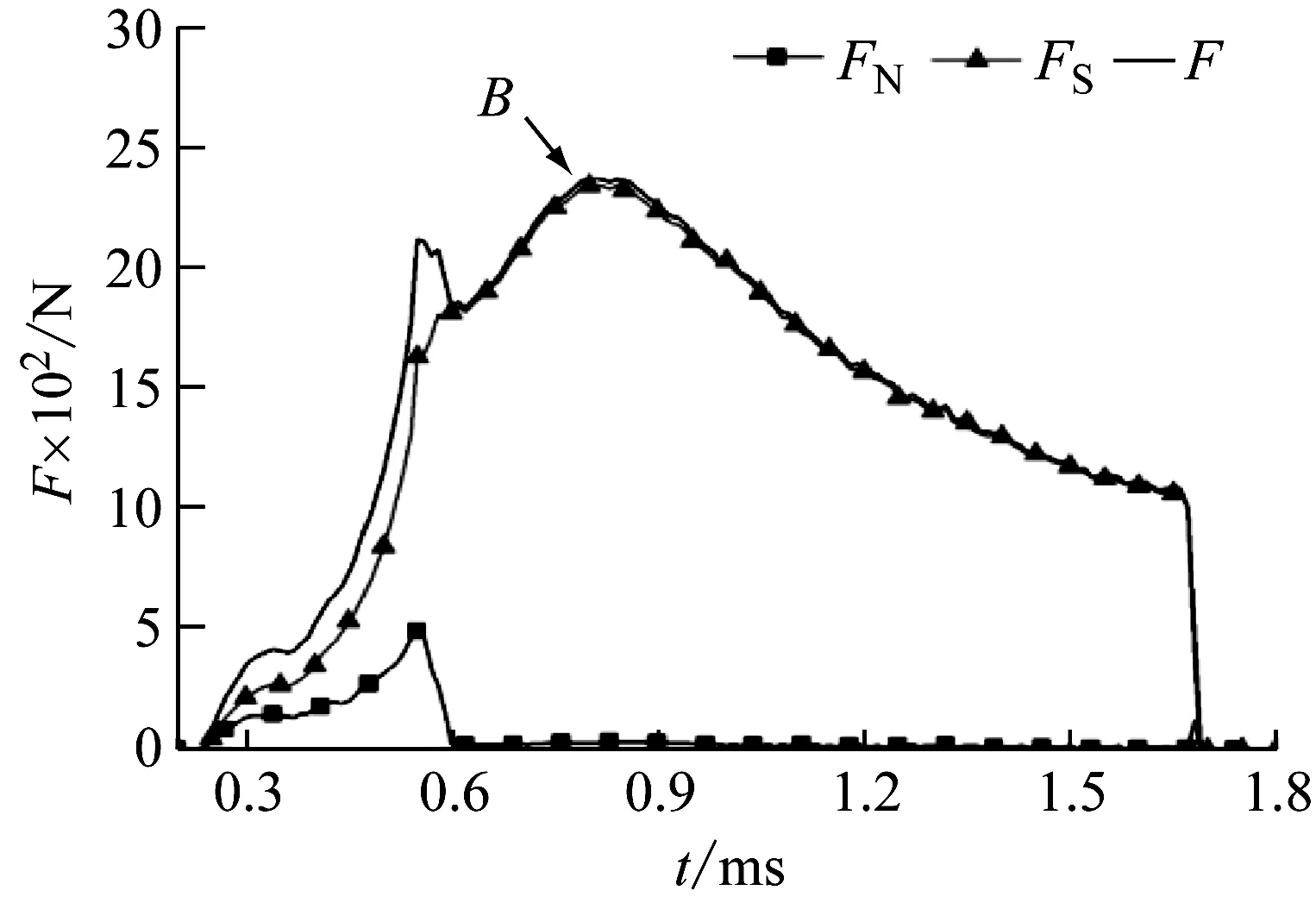
图9 弹头轴向受力Fig.9 Force conditions in axial

轴向正压力FN为坡膛结构导致，在弹头挤进完成之后基本消失，轴向摩擦力FS为弹头受到来自枪管的径向挤压力造成，自弹头接触枪管开始产生直至飞离枪口时消失，二者之和为弹头所受轴向阻力。图9中所示弹头轴向摩擦力为轴向阻力主要组成部分，在挤进完成之后基本等于轴向阻力，且上升至最大值B点后逐步降低，直至弹头飞离枪管而迅速消失，这种变化趋势是弹头膛内发射的轴向阻力特性。

轴向摩擦力与弹头所受径向挤压力正相关，径向挤压力又与单元内部的应力正相关。如图10所式为轴向摩擦力、弹头位移与枪管阳线单元的应力关系图，数字1～5表示5个不同轴向位置处的阳线单元内部应力值变化趋势，由1～5轴向位置不断增大，当弹头运动至某轴向位置处时，该处阳线单元的应力值急剧上升至峰值，当弹头与之脱离接触之后应力基本降至为0。由图10可以看出随着轴向位置的增大，阳线单元内部应力峰值逐渐降低，表明弹头与枪管之间的径向力逐步降低，因而导致轴向摩擦力降低，轴向摩擦力与不同轴向位置处的阳线单元应力峰值变化趋势基本一致。

图10 轴向摩擦力与阳线单元应力关系图Fig.10 Friction force in axial and Mises of land

3.2弹头壳应力应变分析

弹头壳在发射过程中是承受枪管作用力的主要结构，枪管阳线挤压弹头壳而形成刻痕，因此需要重点分析弹头壳的应力应变分布情况。图11和图12为弹头壳沿周向单元的应力/应变-时间曲线，其中1～3为刻痕区域单元，4～7为非刻痕区域单元应力/应变-时间曲线，1～7周向位置如图13所示。

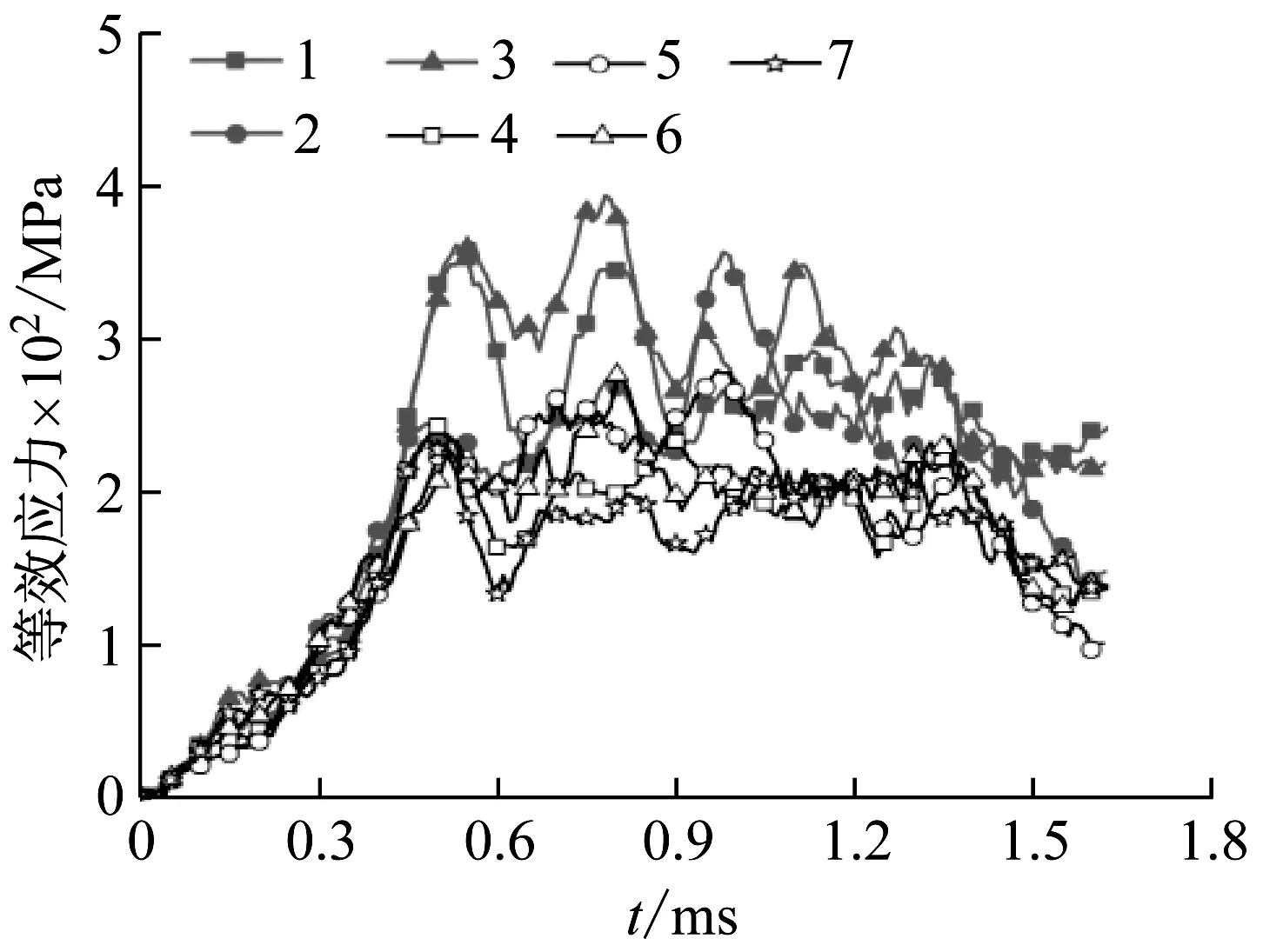
图11 弹头壳沿周向单元的应力-时间曲线Fig.11 Mises-time curve of bullet jacket in circular

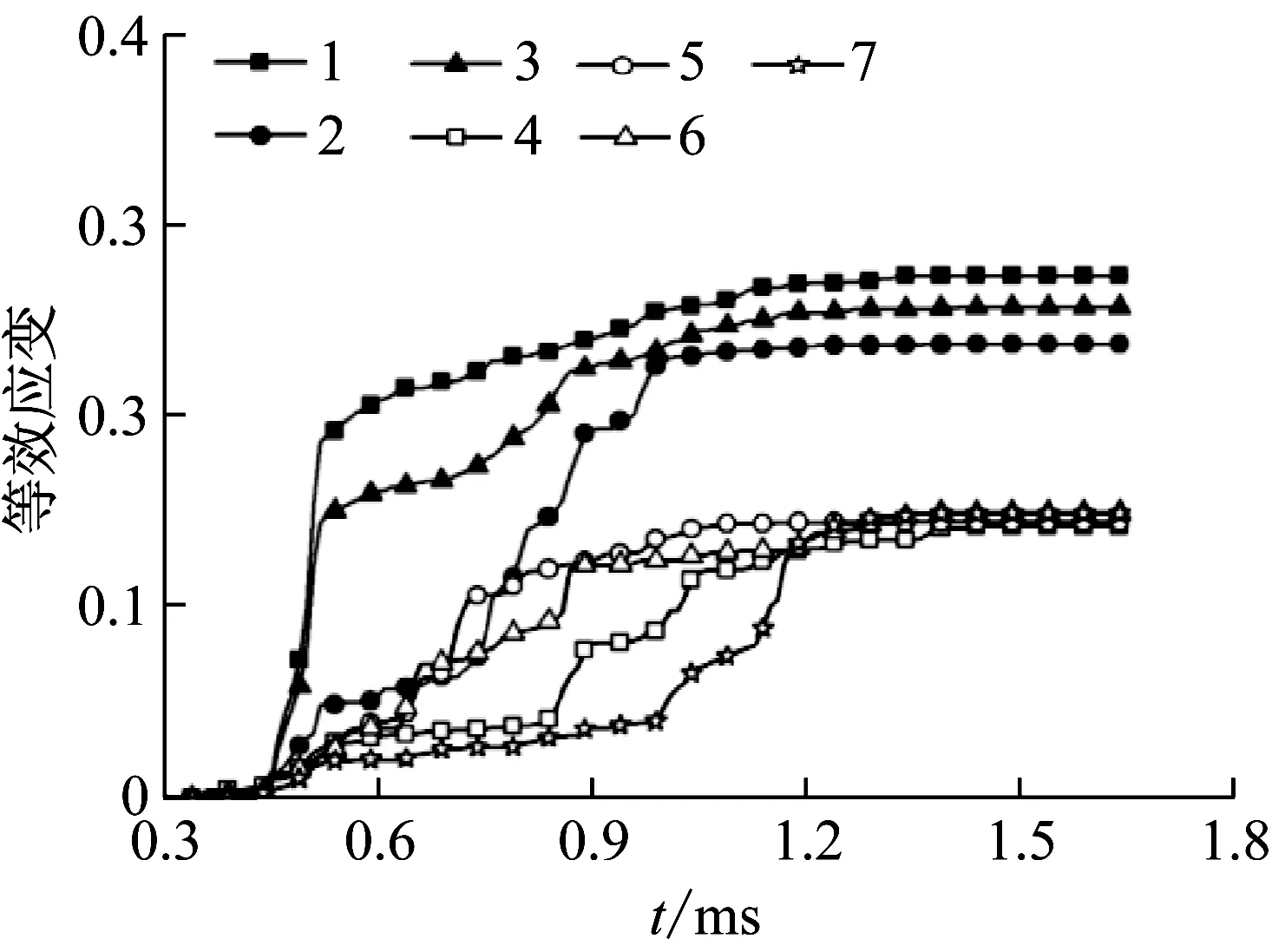
图12 弹头壳沿周向单元的应变-时间曲线Fig.12 Strain-time curve of bullet jacket in circular

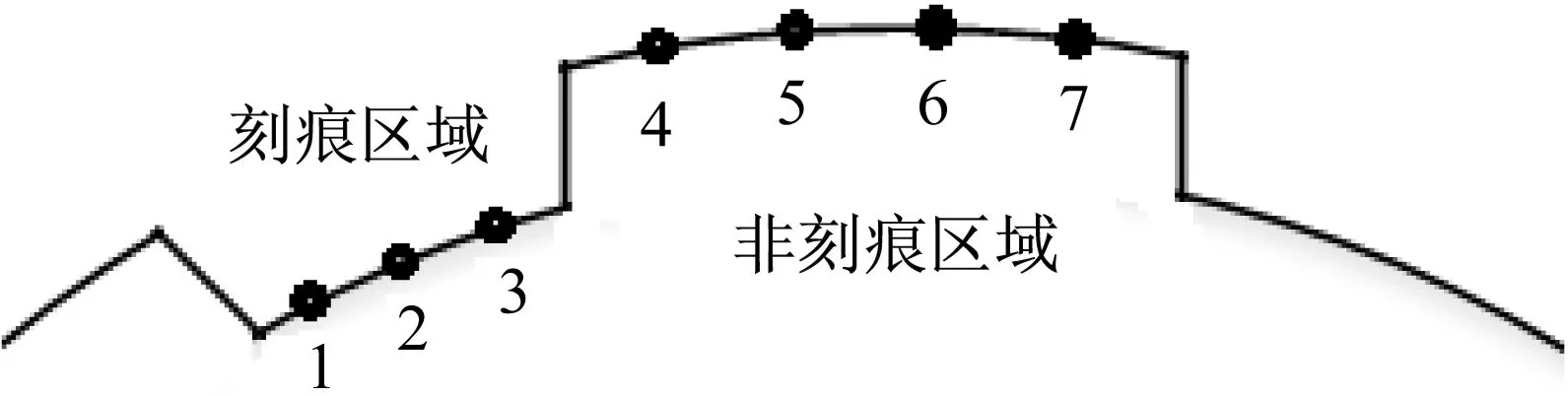
图13 弹头壳单元周向位置示意图Fig.13 Location of bullet jacket element in circular

由于刻痕区域单元的形变量比非刻痕区域大，因而刻痕区域单元应力与应变均高于非刻痕区域单元，平均应力值高42.8%，平均最大应变高72.4%；应力在挤进完成后逐步下降并具有波动性，应力下降的主要原因是动态效应，弹头壳表面应力/应变较高，而内部应力/应变较低，在弹头膛内运动过程中，表面高应力区域将向内部低应力区域扩散，因而出现表面应力下降的现象，这也是弹头轴向摩擦力减低的原因；应力波动性主要是由弹头摆动所引起。

应变在挤进完成后仍继续增大。由于形变量相同，非刻痕区域各位置处的应力、应变值最终基本相同；膛线两侧形状为突变结构，应力集中现象突出导致刻痕两侧应变最终高于刻痕中部区域，此外，刻痕区域的导转侧(1所示位置)承受膛线导转力，因此导转侧的应力与应变略高于非导转侧。1与3两处位于刻痕区域两侧，其应变增长速度远大于其它位置，在挤进完成之后已完成最大应变量的80%左右，其它位置的应变仅为最大应变量的25%左右，表明刻痕两侧在挤进时首先产生较大程度应变，而后其它位置应变逐步大幅增加，刻痕中部(2所示位置)应变在挤进完成后增长速度较大。非刻痕处单元沿周向的应力/应变变化趋势与刻痕处基本一致，在(0.6 ms，1.2 ms)内非刻痕中部5、6位置的平均应力值逐渐减低，两侧4、7位置的平均应力逐渐增大，应变的变化趋势与应力相同，在1.2 ms之后各位置处单元平均应力与应变基本相同。

3.3有无重力作用下枪口振动特性分析

弹头发射前，枪管因自身重力会产生弯曲，枪管轴线变为曲线，图14所示为弹/枪相互作用数值计算模型计算所得枪管弯曲及等效应力分布状态，图中枪口下垂被放大了500倍，枪口下降了0.127 mm。发射过程中，枪口将发生振动现象，如图16所示为枪管有无重力作用下枪口振动位移归一化曲线，其中箭头为枪口移动方向；AX与AY为有重力作用时枪口在X、Y方向的极大值；BX与BY为枪口在X、Y方向的极小值；aX与aY为无重力作用时枪口在X、Y方向的极大值；bX与bY为枪口在X、Y方向的极小值。

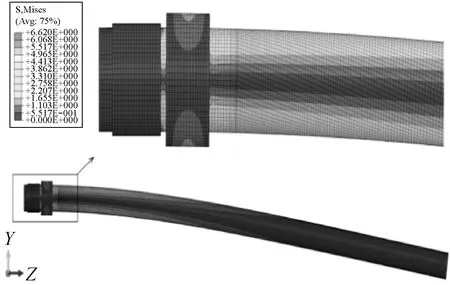
图14 枪管弯曲及等效应力分布状态Fig.14 Bend state of rifle and distribution state of Mises

图15所示，枪口在X-Y平面内的振动位移轨迹线与某种利萨如图形(Lissajous-Figur)相似，利萨如图形轨迹线主要分布在第一、第三象限内，振动轨迹所形成的面积越大则射弹散布越大[8]。图15中重力作用改变了枪口的振动轨迹，总体上看，有重力时的枪口振动轨迹所形成的面积要大于无重力状态，枪口振动轨迹首先在X方向达到极值点(AX、BX)，而后在Y方向达到极值点(AY，BY)，无重力时的顺序与此相反，此外，有重力时枪口振动的极值点要大于无重力状态，表明有重力状态下的射弹散布高于无重力状态，因而在进行理论计算时需要考虑重力作用对弹头膛内发射过程的影响。

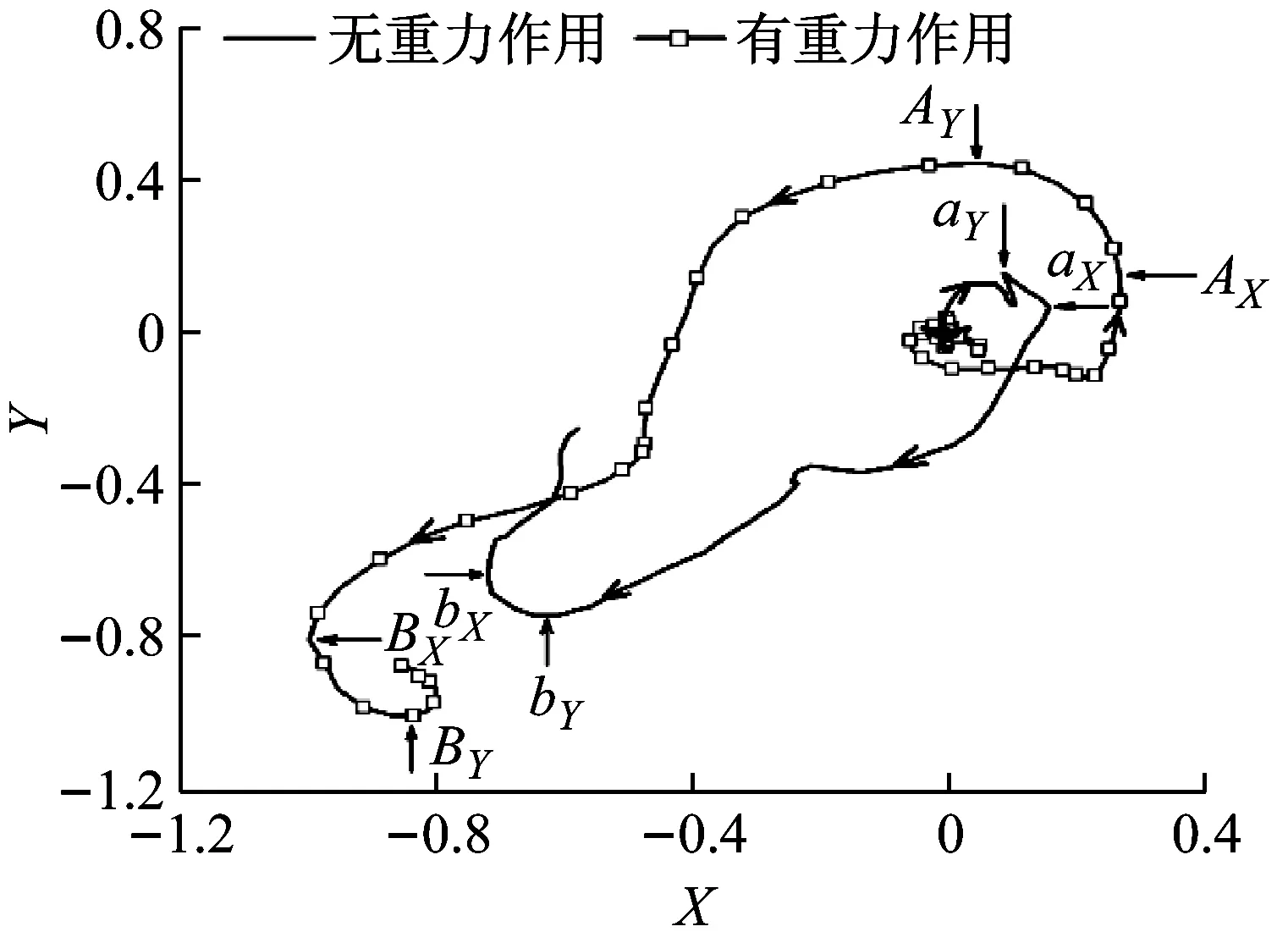
图15 枪口在X-Y平面的振动位移轨迹Fig.15 Vibration displacement of muzzle in X-Y plane

3.4有无重力作用下弹头膛内摆动特性分析

弹头初始扰动与弹头膛内摆动状态密切相关，弹头膛内摆动剧烈则初始扰动大。图16和图17为有无重力作用下弹头摆动情况，其中弹头摆动角(θ)为弹轴与弹头质心速度方向间的夹角，其单位以密位(mil)表示。

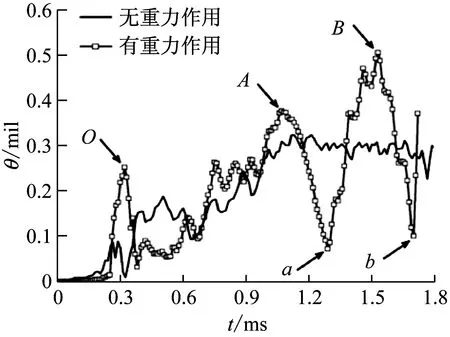
图16 弹头摆动角Fig.16 Swing angular of bullet

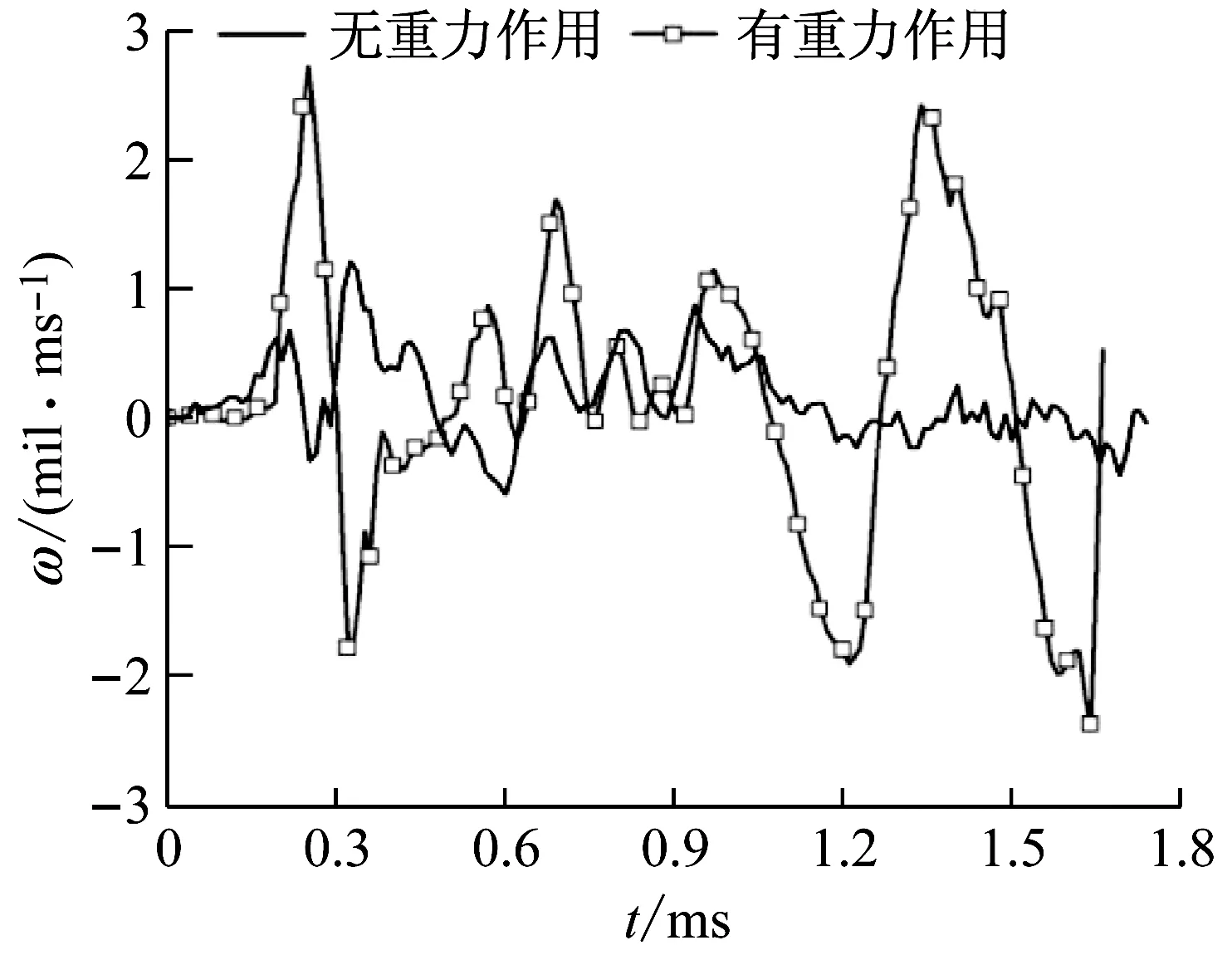
图17 弹头摆动角速度Fig.17 Swing angular velocity of bullet

图16所示，弹头摆动角变化规律受重力影响较明显，有重力作用时的弹头摆动角位移的波动性较大。当弹头开始接触弯曲枪管时，水平弹体受到弯曲枪管的强制改向，因而产生一个较大幅度的摆动，如图中O点所示。当弹头继续沿弯曲枪管轴线运动时，弹头质心速度方向不断被枪管强制改变至弯曲轴线的切向，同时由于弹头轴向速度的增加，弹头摆动角在膛内不断增大，同时具有波动性，图中所示弹头摆动角共经历了3次波动，A、B、a与b4点所示为摆动角极大值与极小值，其中B点值为0.505 mil，a点值为0.073 mil,二者相差约0.432 mil。B点是弹头膛内摆动角最大值，由于弹头在膛内的摆动规律大致相同，B点值越大则摆动角及摆动角速度越大，摆动角及摆动角速度越大则初始扰动越大，因而B点值作为初始扰动的标识量。当无重力作用时，弹体摆动相对较为平稳，摆动角逐渐增大，摆动角的增大主要与轴向速度的增加有关。

图17所示为弹头摆动角速度的变化规律，弹头的摆动角速度变化规律客观上反映了摆动角的变化规律，可以看出有重力作用时的摆动角速度波动性亦高于无重力作用时的计算结果，有重力作用时弹头最大摆动角速度约在±2.5 rad/s内，无重力时最大摆动角速度在-0.6～1.2 rad/s内，值得说明的是，在0.2～0.4 ms时间段的挤进过程中，枪管弯曲导致的弹头摆动角速度具有较大波动，最大摆动角速度值达到2.7 rad/s，然而摆动角位移并不大，表明挤进过程时期的弹头摆动特征为幅值小、速度大。

有无重力作用状态下，弹头头部在膛内的空间位移归一化曲线如图18、图19所示，虚线为空间位移曲线在各平面内的投影。无重力时弹头头部位移曲线呈螺旋状，初始运动阶段(Z≤50 mm)受挤进过程的影响，弹头头部摆动较为混乱且位移值较小，此后摆动位移逐步增大，并逐渐遵循螺旋线规律进行摆动；无重力时弹头在轴向前进了250 mm左右时，弹头头部摆动位移在X、Y方向基本达到最大值。有重力时弹头头部运动是转动和下移的合运动，其空间轨迹线为不断下降的螺旋线；在轴向前进了200 mm左右时，弹头头部摆动位移在X方向达到最大值。

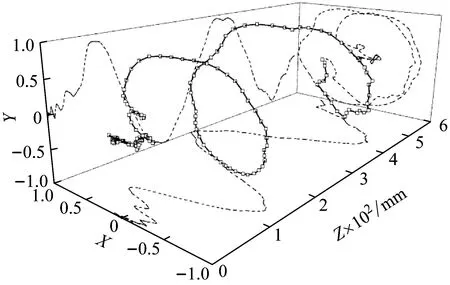
图18 无重力状态下弹头头部空间位移曲线Fig.18 Displacement of bullet head without gravity

弹头头部在X-Y面内的归一化位移曲线如图20、图21所示，无重力作用时弹头头部在X-Y面位移轨迹线近似为圆形，表明弹轴不断绕质心速度方向转动；有重力作用时弹头头部位移在X-Y面内的位移轨迹为左右摆动且不断向下。

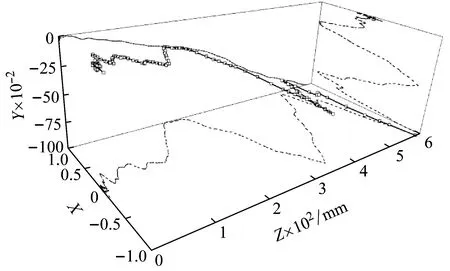
图19 有重力状态下弹头头部空间位移曲线Fig.19 Displacement of bullet head under gravity

重力作用对弹头发射过程的影响主要体现在三个方面，首先是导致枪管弯曲，直接影响弹头在膛内竖直方向的运动；其次枪管弯曲导致其应力分布状态不同于无重力状态，表现为枪管上部分单元承受拉压力，下部分承受压应力，应力分布状态是发射初始状态的一部分，影响内弹道过程中弹/枪的相互作用过程；第三，重力作用于弹头，间接影响其摆动角及摆动角速度。这三个方面将直接或间接改变弹头在膛内的运动状态，产生了有无重力状态下的弹头运动差异现象。

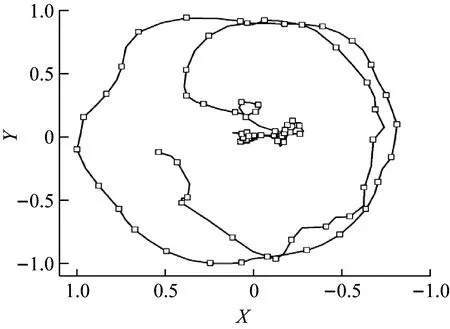
图20 无重力时弹头头部在X-Y面位移曲线Fig.20 Displacement of bullet head in X-Y plane without gravity

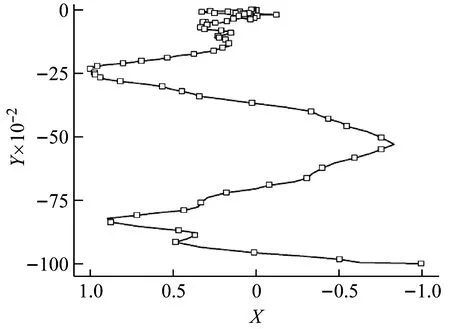
图21 有重力时弹头头部在X-Y面位移曲线Fig.21 Displacement of bullet in X-Y plane head under gravity

4 结 论

(1) 为研究弹头膛内发射过程，揭示弹/枪相互作用机理，以某型狙击步枪为研究对象建立了弹/枪相互作用数值计算模型，模型考虑了挤进过程、重力作用及膛压生成与弹头运动之间的耦合作用，是一个较为完善的求解弹头发射过程的理论模型；通过对比试验结果与数据计算结果，证明了数值计算模型的正确性。

(2) 弹头膛内轴向阻力由轴向正压力与轴向摩擦力组成，其中轴向摩擦力为主要组成部分；在挤进完成之后，轴向正压力基本消失，轴向摩擦力持续增加至最大值后逐步降低；枪管阳线单元应力峰值沿轴向位置的变化趋势与弹头所受轴向摩擦力一致。

(3) 弹头壳沿周向单元的应力/应变分布较为不同，刻痕处平均应力、应变高于非刻痕处42.8%与72.4%；弹头壳周向单元应力在挤进完成后呈现下降趋势，而应变将继续产生较大程度增加；刻痕两侧的应变增长速度明显高于其它位置，挤进完成时即已达到最大应变的80%左右，其它位置应变仅为最大应变的25%左右。

(4) 枪管在弹头发射之前因重力而产生弯曲，枪口下垂位移为0.127 mm；枪口在X-Y面内振动位移轨迹与某种利萨如图形相似，重力作用改变了枪口振动轨迹，并导致枪口振动程度加剧，振动轨迹所形成的面积大于无重力状态。

(5) 弹头膛内摆动因重力作用具有明显波动性，膛内阶段弹头摆动角波动约3次，最大膛内摆动角达到0.505 mil，极大值与极小值最大相差约0.432 mil；弹头摆动角速度范围因重力作用增大约2倍，且摆动角速度波动性明显，故在进行弹头发射过程计算时不可忽略重力作用。

[1] JIANG X, CHEN Z, FAN B, et al. Numerical simulation of blast flow fields induced by a high-speed projectile [J]. Shock Waves, 2008, 18(3):205-212.

[2] GU B, DING X. A refined quasi-microstructure model for finite element analysis of three-dimensional braided composites under ballistic penetration [J]. Journal of Composite Materials, 2005, 39(8):685-710.

[3] 林秉奇. 基于弹炮耦合的火炮非线性动态特性分析与研究[D]. 南京：南京理工大学, 2013.

[4] 顾玮. 弹带挤进及火炮内膛损伤的数值模拟研究[D]. 南京：南京航空航天大学, 2013.

[5] 孙河洋, 马吉胜, 李伟,等. 坡膛结构变化对火炮内弹道性能影响的研究[J]. 兵工学报, 2012, 33(6):669-675.

SUN Heyang, MA Jisheng, LI Wei, et al.Study on influence of bore structure on gun’s interior ballistic performance[J]. Acta Armamentarii, 2012, 33(6):669-675.

[6] SOUTH J, YIOURNAS A, WAGNER J, et al. A study of the engraving of the M855 5.56-mm projectile:ARL-TR-4743[R]. Army Research Laboratory, 2009.

[7] 周彦煌. 实用两相流内弹道学[M]. 北京:兵器工业出版社, 1990.

[8] 吴三灵.火炮动力学试验[M].北京:国防工业出版社, 2004.

Numericalcalculationontheinteractionbetweenbulletandsniperrifle

LIU Guoqing，XU Cheng，DING Chuanjun

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

The numerical calculation model for the interaction between bullet and sniper rifle was established to deeply study the launch process of bullet based on the nonlinear finite element theory. The model integrated the calculation programs for the bore pressure and the launch process, which was able to reflect the real relation between the bore pressure and bullet motion. The engraving process and the subsequent ballistic process were combined in this model to ensure the integrity of internal ballistic. The barrel pre-bent condition caused by gravity was also considered. The model is a comprehensive theoretical model to calculate the launch process. Its accuracy was proved by comparing experiment and calculation results. The force conditions, stress-strain distributions, swing angle of bullet and vibration of muzzle in the gravity field were obtained numerically, which reveals the interaction mechanism between bullet and rifle.

sniper rifle; interaction; numerical model; engraving process; coupling calculation; gravity action

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.19.001

国家自然科学基金(51575279)

2015-12-31 修改稿收到日期：2016-05-05

刘国庆 男，博士生，1988年10月生

徐诚 男，博士，教授，1962年10月生