基于行波分解的泛频响函数法在高承台桩灾后无损检测评估中的应用研究
2017-11-06李振亚王奎华吴文兵
李振亚,王奎华,吴文兵
(1. 浙江大学 滨海和城市岩土工程研究中心, 杭州 310058;2. 中国地质大学 工程学院, 武汉 430074)
基于行波分解的泛频响函数法在高承台桩灾后无损检测评估中的应用研究
李振亚1,王奎华1,吴文兵2
(1. 浙江大学 滨海和城市岩土工程研究中心, 杭州 310058;2. 中国地质大学 工程学院, 武汉 430074)
针对现有方法在高承台桩灾后无损检测和评估中的局限性,提出了基于行波分解的泛频响函数法。将承台对桩顶的作用简化为黏弹性支撑边界,采用自行编制的波动分析程序求得检测截面处的泛频响函数;通过在该位置虚拟输入半正弦激励脉冲,将泛频响函数所包含的信息转换到时域内进行分析,得到检测截面以下虚拟隔离单桩桩顶的速度时域响应曲线;分析了相关参数对泛频响函数和由此转换而来的时域响应的影响。结果表明,基于行波分解的泛频响函数法,能在不破坏上部结构的前提下,完全消除其对检测结果的影响,从而将复杂结构体系下的基桩转化到单桩模式下进行检测分析,简化了检测步骤,降低了分析难度。
桥梁工程;无损检测;泛频响函数;高承台桩;行波分解;波动分析程序
高承台桩是桥梁、码头等工程中常用的基础形式,大规模的自然灾害(如破坏性地震、滑坡等)、人为事故(如车辆和船舶的撞击等)以及水流腐蚀等都会对其造成不同程度的破坏。地表(水面)以上可见部位的破坏容易检测,而地表(水面)以下部位的桩身由于具有隐蔽性,其检测评估工作具有很大难度。
基桩的完整性检测工作对于保证工程质量具有非常重要的作用,历来为研究人员所重视,不断有新的检测理论和检测方法提出,包括有损检测方法和无损检测方法,其中无损检测方法发展更为迅速,应用也更为广泛。无损检测方法大致可划分为两大类:一类是反射法,如脉冲响应法、反射波法和冲击回波法等;一类是透射法,如跨孔声波测井法和旁孔透射波法等。
反射法具有方便快捷、费用低廉的优点而被广泛采用,在检测时通常要求桩顶为自由端,这对处于打桩结束阶段的基桩的质量检测十分适用。但在役的桥梁及码头工程中常用的高承台桩带有承台、面板、横梁和纵梁等上部结构,会对信号的传播产生复杂的反射、透射等多重干扰,甚至会掩盖桩底反射信号而使得误判的概率增大。徐攸在等[1]通过对天津港码头的一根上部带有梁板的桩进行低应变测试,指出梁板对上行波的反射极大地改变了时域曲线的波形,并使得桩底反射信号难以辨别。孙熙平等[2-5]采用数值模拟和试验的方法分析了应力波在承台-桩系统中传播的规律,结果表明应力波经过各个接触面的反射和叠加之后变得十分复杂,采用反射波法检测桩的完整性可行性较差。一些学者对传统的反射法进行改进,以期获得合理评估桩身完整性的方法。Addison 等[6-7]首先将小波变换应用于低应变检测中,基于小波变换的信号分析方法较传统傅里叶变换法的优势在于,小波变换能够同步产生时间和范围信息[8],但在检测较小比率的缺陷时则存在很大局限[9]。Lo等[10]将小波变换与反射波法相结合应用于时-频域分析,提高了测试分析的精度,一定程度上克服了传统反射法的缺陷,但由于上部结构的形式十分复杂,采用小波变换并不能将各种反射信号的影响都有效消除。Gassman等[11]通过现场试验和数值模拟指出,对于脉冲响应法,当频率低于截止频率时,该方法可用于带承台桩的检测,但截止频率受到承台的形状和尺寸的限制,局限性很大。反射法考虑了上部结构的具体形式对桩身信号传播的影响,再试图通过技术人员的判断去消除这种影响,因而具有很大的局限性,由于上部结构的形式复杂多样,很难得到一种可以普遍适用的方法。
与反射法中接收装置置于桩顶不同,旁孔透射波法的接收装置置于桩旁预先钻好的孔内,接收经桩身传播到孔内的首至直达波,不受上部结构的影响,因而在既有结构物下的桩基检测中得到了众多学者的重视。Davis[12]率先提出用旁孔透射波法检测既有结构物下桩的长度,随后Davis等[13-14]对这一方法进行了细致的研究,指出旁孔透射波法不仅可以检测既有结构物下桩的长度,而且可以检测桩身的严重缺陷。Ni等[15]分析了钻孔倾斜对桩长判定产生的误差,指出桩长判定的误差在5%~20%,且随着钻孔倾斜角度的增大而增大。Huang等[16-17]采用三维有限元对旁孔透射波法进行了模拟,并对比了饱和土和非饱和土情况下旁孔透射信号的区别。Liao等[18]通过引入修正因子以提高分析的精确度。陈龙珠等[19-22]还将旁孔透射波法应用于桩底深度的确定和水泥搅拌桩的质量检测工作。透射法检测时需要预先在桩旁钻孔,过程费时费力,尤其对于桥梁、码头等水上工程,钻孔十分不便,有时甚至无法实现;另外,信号沿桩身向下传播时会逐渐衰减,深度过大时,透射到土层中的信号会很微弱而难以测定,从而无法判定桩身完整性情况。
综上所述,现有检测方法在高承台桩的完整性检测和评估中均存在各自的局限性,鉴于此,本文提出一种基于行波分解的泛频响函数法,能够在不破坏上部结构的前提下,完全消除其对检测结果的影响,从而将复杂结构体系下的基桩转化到单桩模式下进行检测分析。
1 泛频响函数原理
杆件(桩)中的一维波动可以分解为两列传播方向相反但传播速度相同的独立的“行波”,波形由初始条件决定。对处于打桩结束阶段的基桩而言,桩顶为自由端,此时用小锤敲击桩顶产生激励脉冲,并用置于桩顶的传感器接收反射信号,反射信号的傅里叶变换与输入激励脉冲的傅里叶变换的比值,称为频率响应函数,其包含了桩长及桩身完整性信息。但是,当桩顶与承台及上部结构相连时,传统的频率响应函数还包含有承台及上部结构的振动信息,直接采用传统的频率响应函数分析桩长及桩身完整性信息已基本不可能。鉴于此,我们提出“泛频响函数”的概念,基本思路如图1所示。
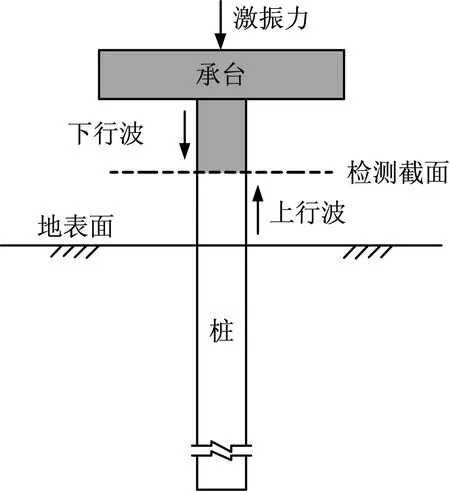
图1 泛频响函数原理示意图Fig.1 Schematic of the principle of universal frequency response function
如图1所示,对于桩顶有承台或其他结构物时,取桩顶以下某一位置作为检测截面,在该截面上方某一部位施加竖向激振力(需使得桩身产生近似的竖向一维波动)。由于初始扰动来自该截面上方,因此该截面位置会首先检测到下行波,此下行波沿桩身向下传播的过程中遇到桩身截面阻抗变化的位置或桩底时会反射产生上行波。虽然检测截面处测得的下行波是该截面以上桩身和承台共同作用的结果,而测得的上行波则是下行波、检测截面以下桩身、桩侧土和桩底土共同作用的结果,但是,检测截面处上行波相对于下行波的变化却仅与检测截面以下的桩身和土体有关。类似于现有的频率响应函数,将检测截面处的下行波看作是对截面以下桩土系统的“输入”,而将该位置处的上行波看作是相对于下行波的一种“输出”,检测截面处上行波与下行波傅里叶变换的比值,即所谓 “泛频响函数”。由定义可知,泛频响函数完全反映了检测截面以下的桩土信息,而与检测截面以上的桩身及上部结构无关,因此能够完全消除上部结构对检测结果的影响。
2 泛频响函数求解


图2 波动分析程序计算原理示意图Fig.2 Schematic of the principle of wave equation analysis program
求解过程中做出以下假设:
(1) 应力波在桩中的传播近似满足一维波动条件;
(2) 对于每一桩段,单元的阻抗变化仅发生在单元界面处,波在单元内部传播时不发生畸变;
(3) 桩土体系的振动近似满足线弹性、小变形条件;
(4) 桩侧土及桩底土对桩的作用均采用单Voigt模型进行模拟;
(5) 桩侧土阻力均作用在单元底部。
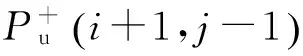
于是,对第i桩段,其所受桩侧土的摩阻力
R(i,j)=Aikis(i,j)+Aiciv(i,j)
(1)
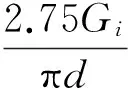
桩底土对桩端的作用力为
Rtoe(j)=Atoektoes(N,j)+Atoectoev(N,j)
(2)
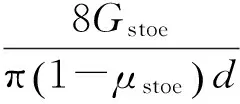
设第i节点桩身截面阻抗为Z(i),定义两个无量纲参数为

(3)

(4)
第j时间单元、第i节点的位移与速度之间存在关系

(5)
由于波在单元内部传播时不发生畸变,故
(6)
(7)
将桩顶激振力f(t)按照时间间隔Δt离散化为f(j),于是
(8)
式中,Ktop和Ctop分别为承台与桩顶之间的刚度系数和阻尼系数。
由式(5)、式(6)和式(8)可得,桩顶的速度
v(0,j)=
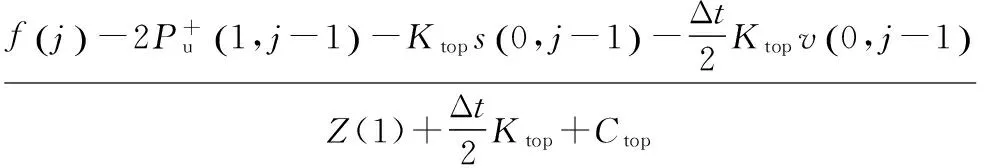
(9)
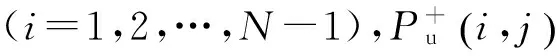

(10)
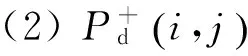
(11)
(3) 第i节点土阻力的激发量
Pu3(i,j)=Tu(i)R(i,j)
(12)
由式(10)~式(12)可得
(13)
同理
(14)
第i节点(i=1,2,…,N-1)的速度可表示为
v(i,j)=
(15)
由式(1)、式(5)和式(15)可得
(16)
对第N节点(即桩端位置),有
(17)
第N节点的速度
(18)
由式(2)、式(5)、式(7)、式(17)和式(18)可得
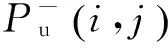
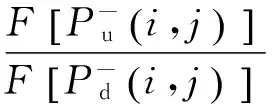
(20)
基于这一算法编制了相应的程序,对检测截面处的泛频响函数进行了计算。求解过程中假设桩为等截面均质杆件,桩侧土均质,基于理论研究的参数取值为:桩长l=20 m,入土长度l1=15 m,检测截面与桩顶的距离lx=4 m;承台对桩顶的复阻抗作用为Ktop=1010N/m、Ctop=1010N·s/m(这两个参数取值越大表示承台对桩顶的约束作用越强,反之则越弱);其他桩土参数见表1。在以下分析过程中,输入激振力近似认为作用于桩顶位置。如图3所示,在具体实施过程中,参考有关学者的处理方法,可在桩顶位置附近粘贴一楔形块,通过敲击楔形块产生一激励脉冲,该激励脉冲通过检测截面时可近似认为沿竖向传播,另外,在实际检测时,激振力施加位置位于检测截面以上一定距离即可。

表1 桩土参数表Tab.1 Parameters of pile and soil
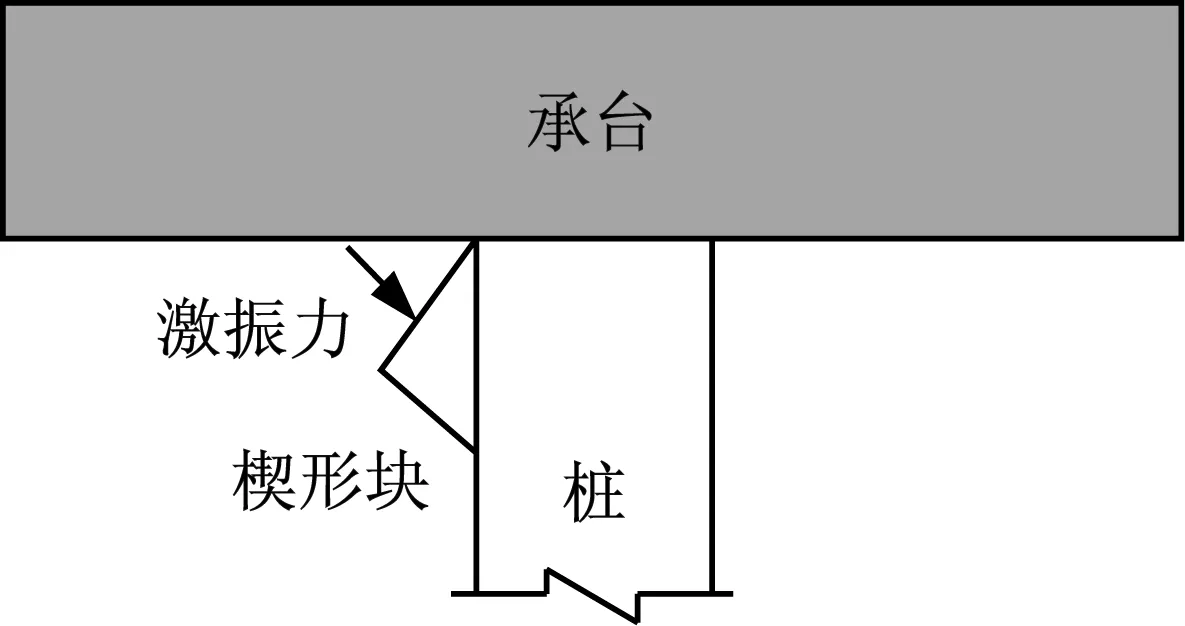
图3 激振力输入示意图Fig.3 Schematic of the exciting force


图4 检测截面处的泛频响函数曲线Fig.4 Universal frequency response function of the test section


(21)
对式(21)进行变换可得
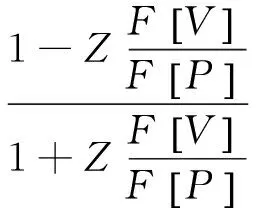
(22)
进一步

(23)
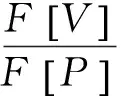
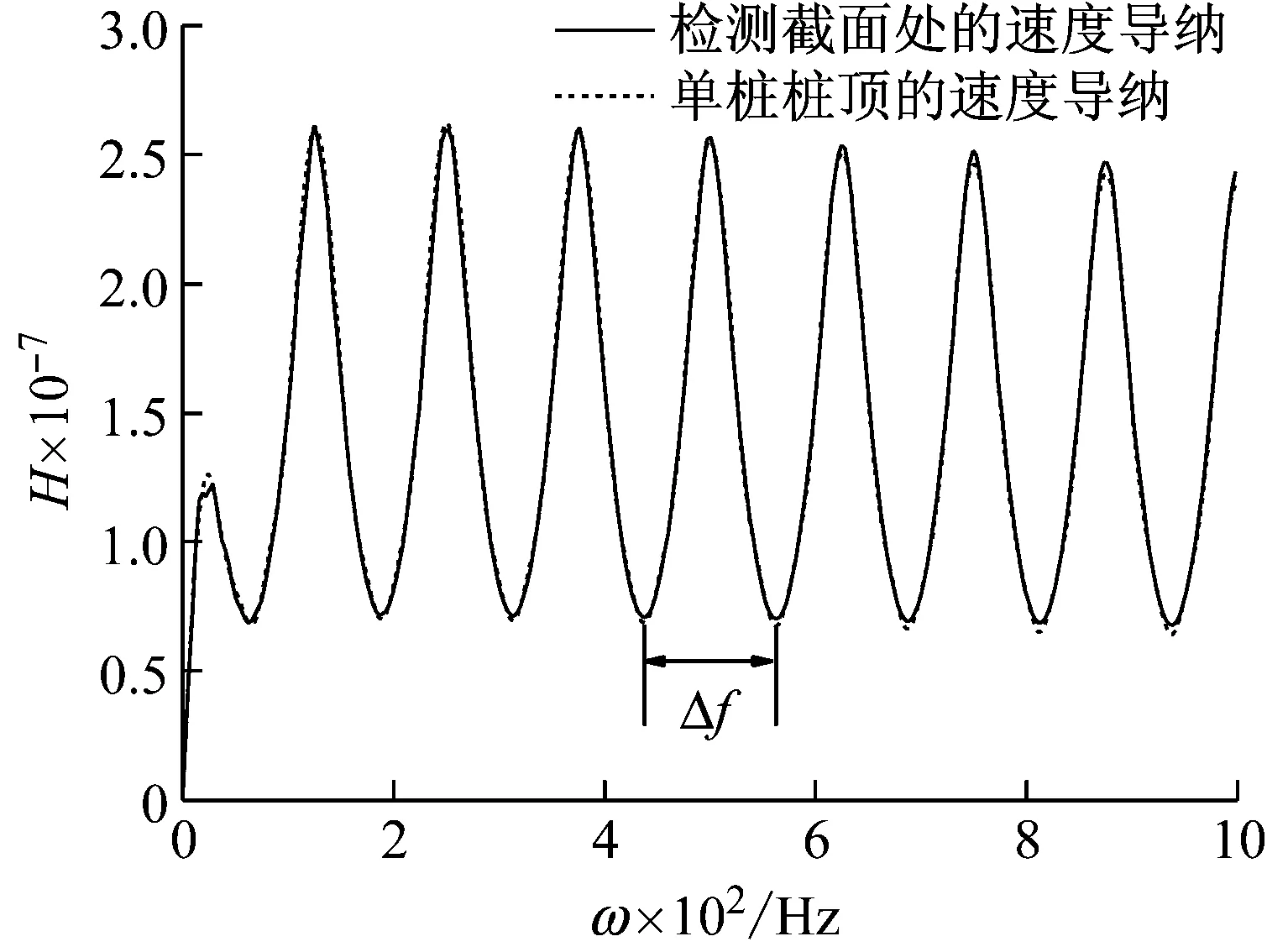
图5 检测截面处的速度导纳与单桩桩顶速度导纳的对比Fig.5 Comparison between the admittance of velocity of the test section and that of the single pile head
若在检测截面处虚拟输入一半正弦脉冲q(t),其傅里叶变换为F[q],则
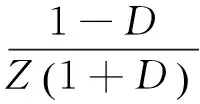
(24)
对式(24)两边同时进行傅里叶逆变换,得检测截面处的速度时域响应为
(25)
将检测截面处的速度时域响应曲线与去除检测截面以上桩身及上部结构后所得单桩的桩顶速度时域响应曲线进行了对比,结果如图6所示。由图6可知,两者完全一致。另外,桩底反射信号与入射脉冲之间的时间间隔Δt=0.008 s,据此得到的桩身长度L=Δt×c/2=16 m,恰好是检测截面以下的桩长。
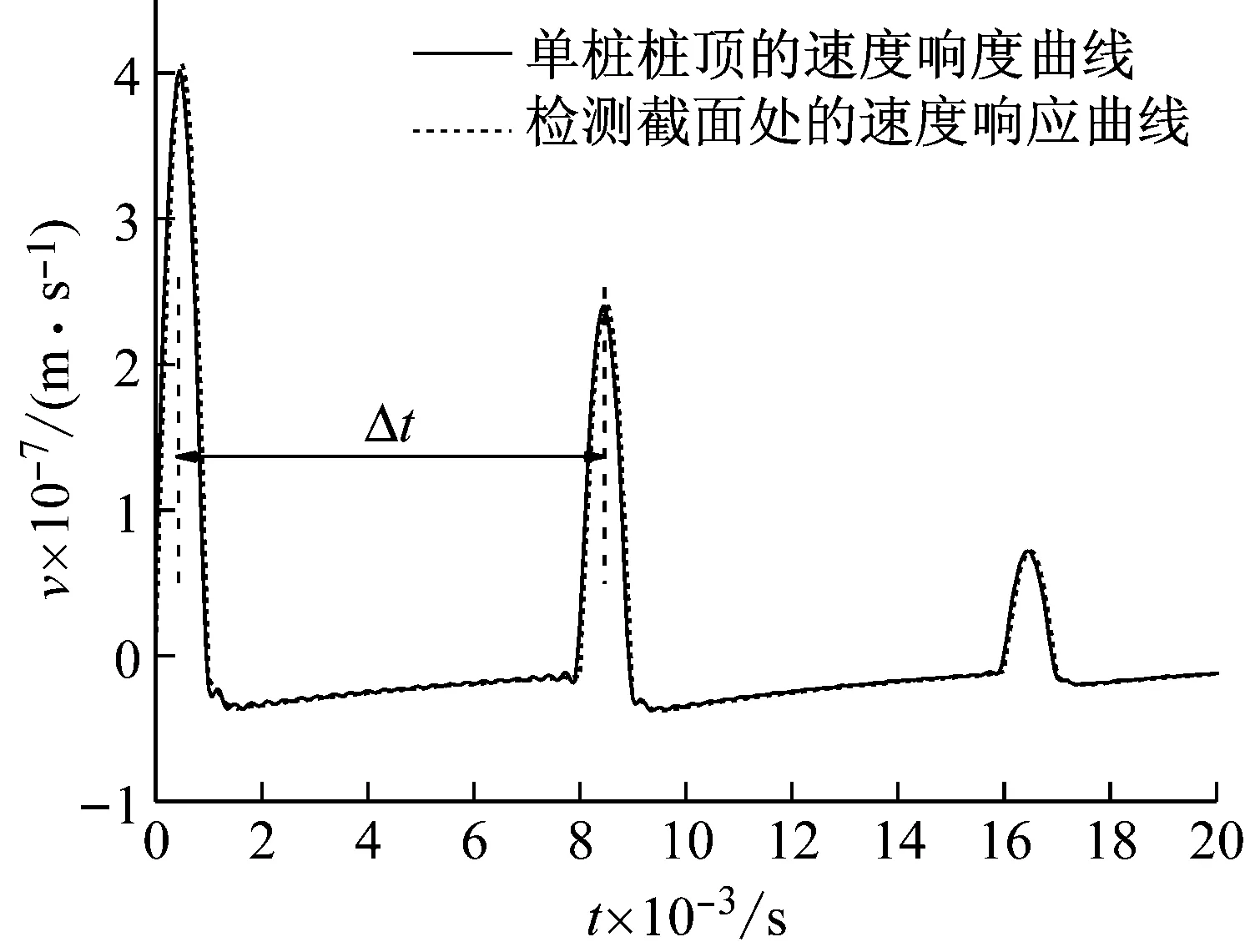
图6 检测截面处的速度时域响应曲线与单桩桩顶的速度时域响应曲线的对比Fig.6 Comparison between the velocity response of the test section and that of the single pile head in the time domain
综上所述,式(20)和式(23)虽然形式上有所不同,但其本质是一样的,反映的都仅是检测截面以下的桩土信息,而与检测截面以上的桩身及上部结构无关。在实际检测工作中,只要采用适当的方法测得检测截面处的速度波和力波信号,通过式(23)或式(25)即可判断出检测截面以下的桩长和桩身完整性信息。
3 参数分析
通过式(20)和式(25)分析相关参数对检测截面处的泛频响函数及由此变换得到的速度时域响应曲线的影响,进一步明确泛频响函数的性质及其在高承台桩无损检测中的适用性。分析过程中,桩长l=20 m,入土长度l1=15 m,检测截面与桩顶的距离lx=4 m;其他桩土参数取值同表1。
3.1承台尺寸的影响
承台的尺寸不同,其对桩顶的阻抗作用也不同,通过弹簧刚度系数和阻尼系数的变化来反映承台尺寸的变化。取三组参数:①Ktop=108N/m、Ctop=108N·s/m;②Ktop=1010N/m、Ctop=1010N·s/m;③Ktop=1012N/m、Ctop=1012N·s/m,分别对应三种工况进行分析。
承台尺寸对检测截面处的泛频响函数的影响如图7所示,由图7可知,三种工况下检测截面处的泛频响函数实部和虚部曲线均完全重合,即承台尺寸的变化对泛频响函数完全没有影响,这与理论分析的结论相一致。
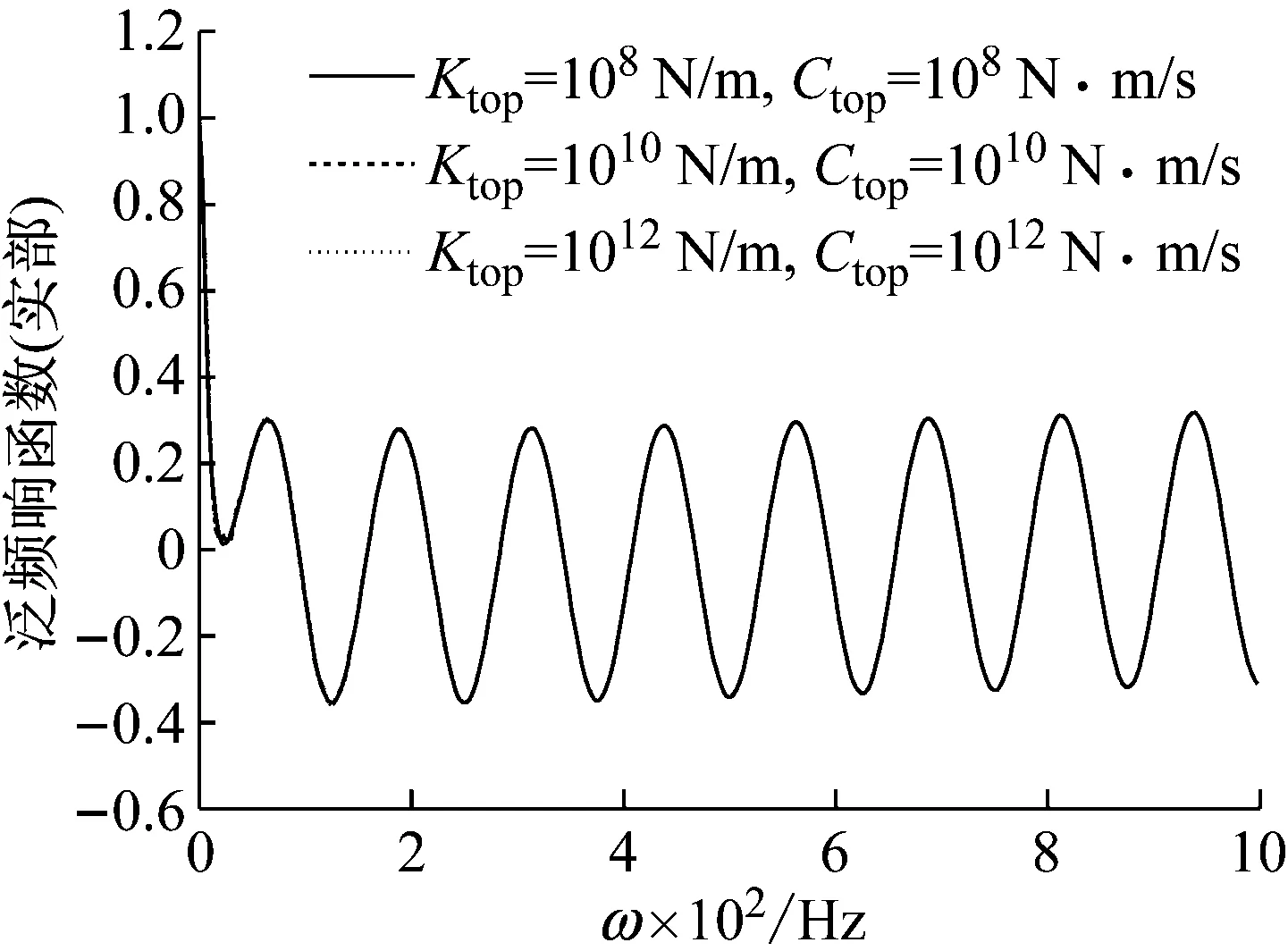
(a)

(b)图7 承台尺寸对检测截面处的泛频响函数的影响Fig.7 Effect of the size of cushion cap on universal frequency response function of the test section
承台尺寸对检测截面处的速度时域响应的影响如图8所示,由图8可知,由于检测截面处的泛频响函数不受承台尺寸变化的影响,因此,经泛频响函数变换得到的检测截面处的速度时域响应曲线也不受承台尺寸变化的影响,且其完全表征了检测截面以下的桩长信息。

图8 承台尺寸对检测截面处的速度时域响应的影响Fig.8 Effect of the size of cushion cap on the velocity response of the test section in the time domain
综上所述,泛频响函数唯一地反映了检测截面以下的桩长及桩身完整性信息,与检测截面以上的桩身及承台无关,且通过适当的变换可将泛频响函数所包含的信息转换到时域内,相当于将检测截面以下的桩身从复杂的结构体系中隔离出来,而转化成单桩问题,大大降低了检测分析难度。
3.2桩侧土剪切波速的影响
分析过程中,桩侧土剪切波速取vs=100 m/s、150 m/s和200 m/s,桩底土剪切波速vstoe=100 m/s,承台对桩顶的复阻抗Ktop=1010N/m、Ctop=1010N·s/m,其他参数取值不变。
桩侧土剪切波速对检测截面处的泛频响函数的影响如图9所示,由图9可知,随着桩侧土剪切波速的增大,泛频响函数的实部和虚部曲线的振幅均逐渐减小,但曲线的波峰(波谷)仍然完全对应。由此可知,桩侧土剪切波速的增大,只是增强了对信号能量的耗散作用,而不会改变泛频响函数曲线所表征的检测截面以下的桩长信息。
桩侧土剪切波速对检测截面处的速度时域响应曲线的影响如图10所示,由图10可知,随着桩侧土剪切波速的增大,桩底反射信号的幅值逐渐减小,但桩底反射信号与入射脉冲之间的时间间距保持不变,据此计算得到的桩长不变,且与检测截面以下的实际桩长一致。

(a)

(b)图9 桩侧土剪切波速对检测截面处的泛频响函数的影响Fig.9 Effect of shear wave velocity of surrounding soil on universal frequency response function of the test section

图10 桩侧土剪切波速对检测截面处的速度时域响应的影响Fig.10 Effect of shear wave velocity of surrounding soil on the velocity response of the test section in the time domain
3.3桩底土剪切波速的影响
分析过程中,桩底土剪切波速取vstoe=100 m/s、vstoe=200 m/s和vstoe=300 m/s,桩侧土剪切波速vs=100 m/s,承台对桩顶的复阻抗Ktop=1010N/m、Ctop=1010N·s/m,其他参数取值不变。
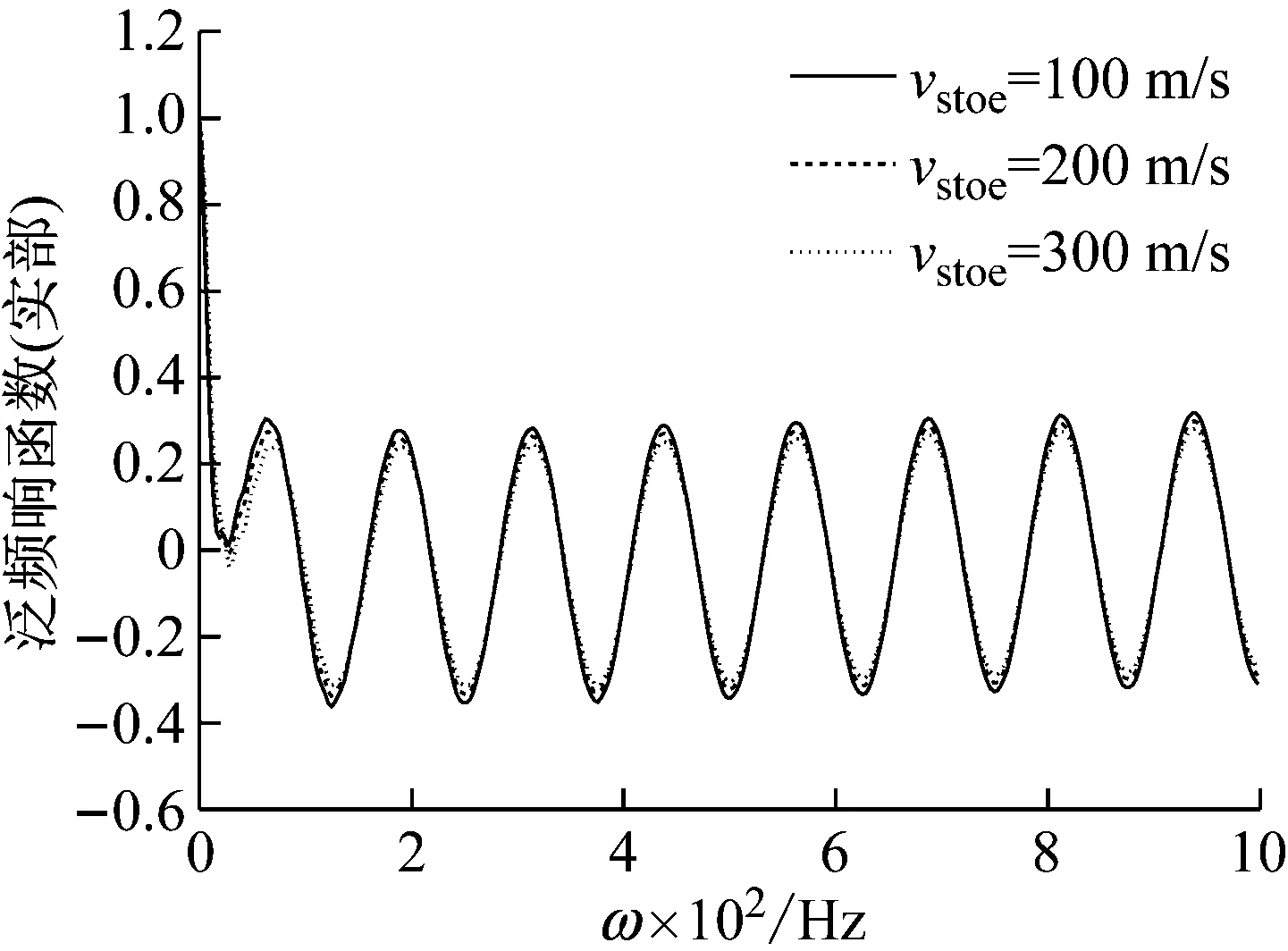
由图11和图12可知,桩底土剪切波速对检测截面处的泛频响函数及由此变换得到的速度时域响应曲线的影响与桩侧土剪切波速一致,即桩底土剪切波速的增大只是增强了对信号能量的耗散作用,而不会改变泛频响函数曲线及速度时域响应曲线所包含的检测截面以下的桩长信息。
(a)
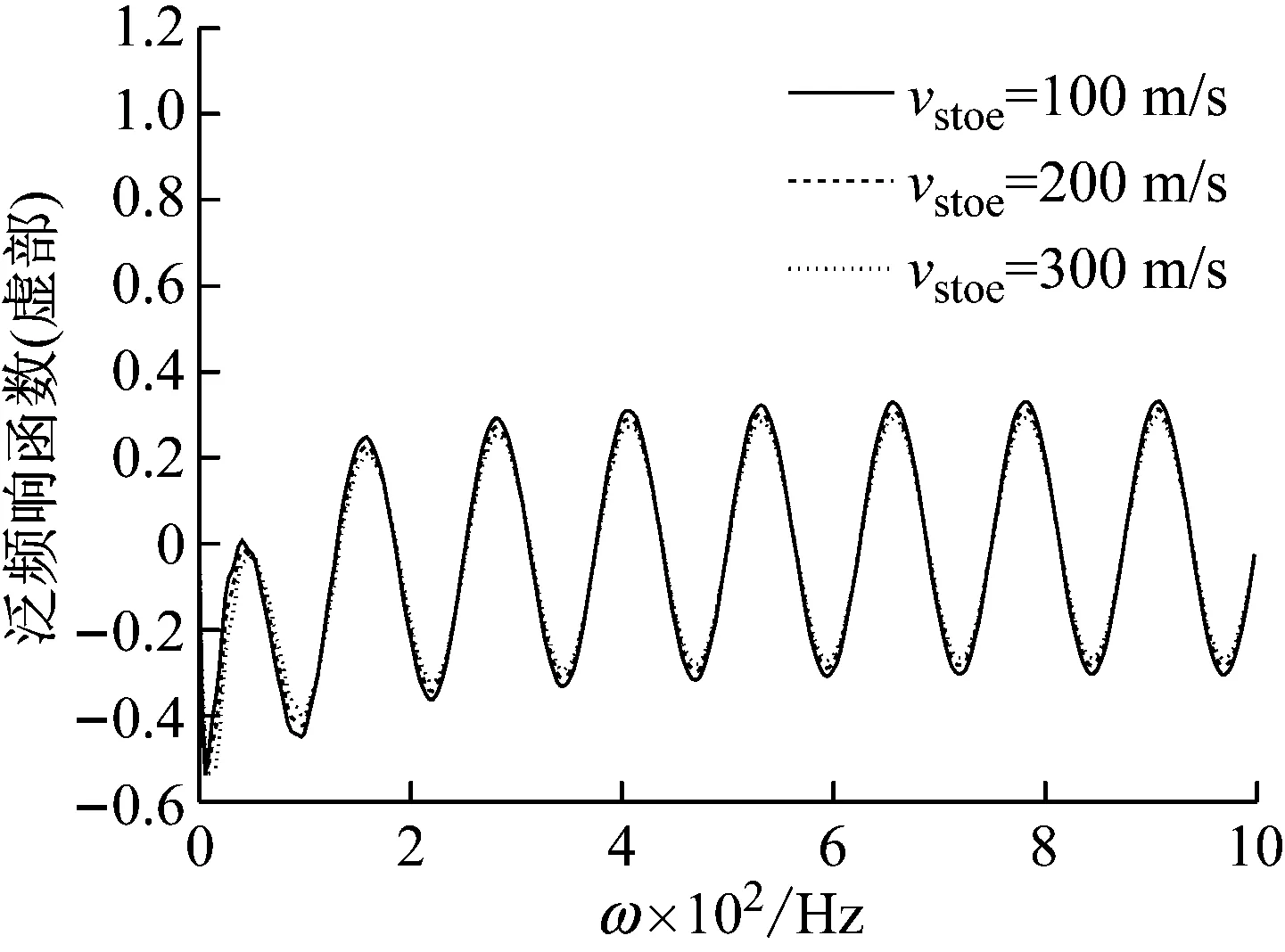
(b)图11 桩底土剪切波速对检测截面处的泛频响函数的影响Fig.11 Effect of shear wave velocity of pile subsoil on universal frequency response function of the test section
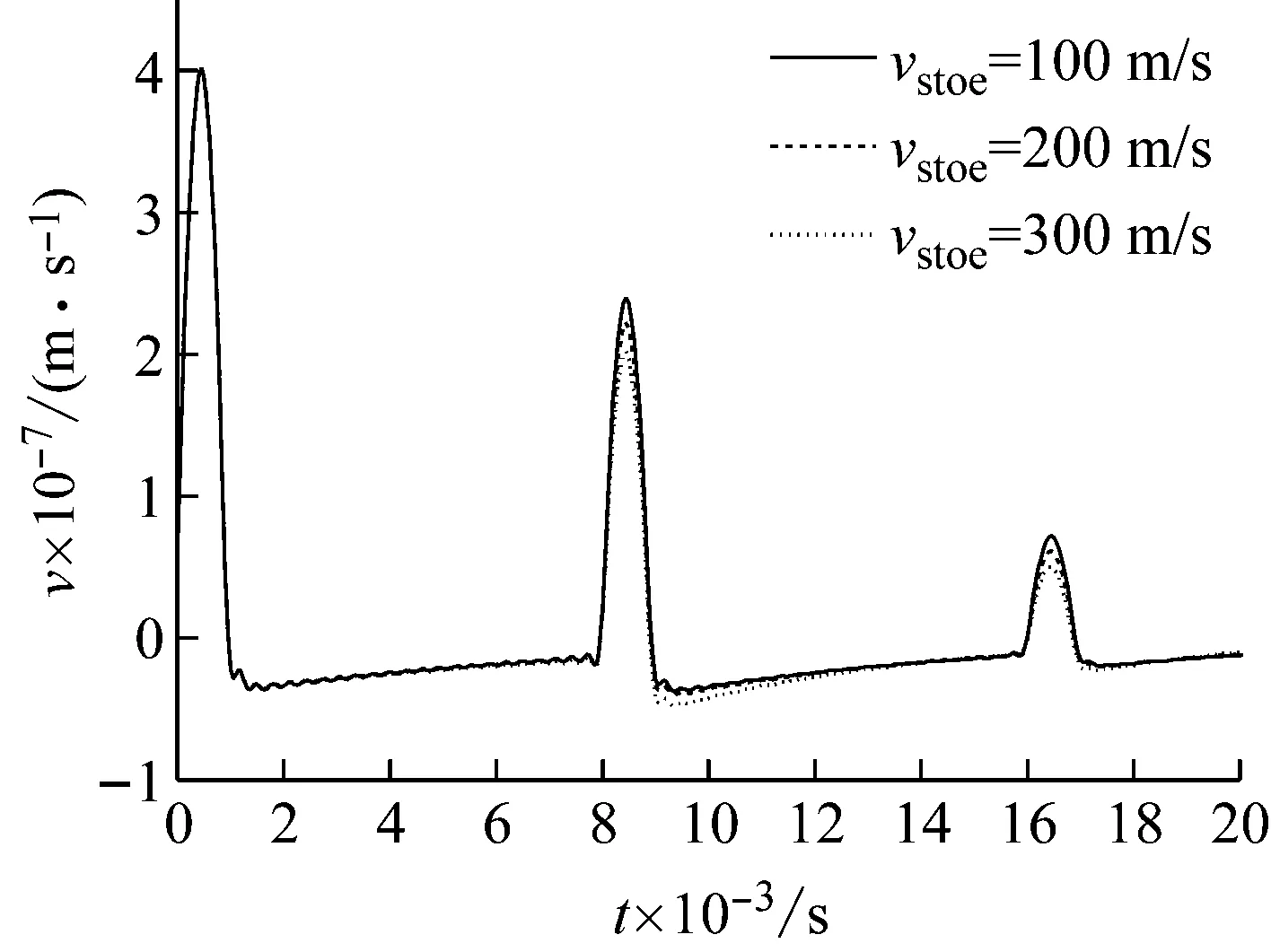
图12 桩底土剪切波速对检测截面处的速度时域响应的影响Fig.12 Effect of shear wave velocity of pile subsoil on the velocity response of the test section in the time domain
3.4桩身缺陷的影响
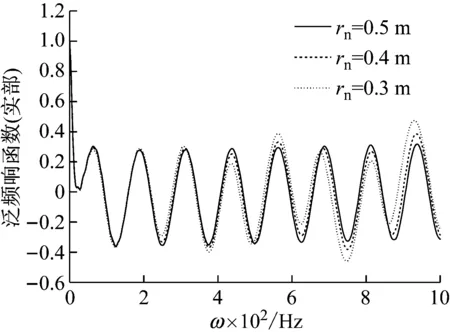
泛频响函数法提出的目的即在于检测既有结构物下的桩身的完整性,因此分析桩身缺陷对泛频响函数的影响,进而对缺陷类型和缺陷位置做出判断,是检验该方法是否可行的最终标准。在地表以下5 m位置处设置缩颈缺陷,缺陷长度设为0.2 m,取缩颈位置处桩身半径rn=0.3 m、rn=0.4 m和rn=0.5 m进行分析,其中rn=0.5 m表示桩身无缩颈缺陷,其他参数取值不变.
桩身缺陷对检测截面处的泛频响函数的影响如图13所示,由图13可知,相比于完整桩,缩颈缺陷的存在使得检测截面处的泛频响函数出现“大峰夹小峰”的现象,且缺陷位置处桩径越小,缺陷程度越严重,夹峰现象就越明显。泛频响函数曲线能够将桩身缺陷准确地反映出来,进一步证明了本文所提方法的可行性。
(a)

(b)图13 桩身缺陷对检测截面处的泛频响函数的影响Fig.13 Effect of the pile defect on universal frequency response function of the test section
如图14所示,泛频响函数经转换得到速度时域响应后,桩身缺陷及其位置都能够更明显地分辨,且缺陷程度越严重,对应位置的同向反射信号就越强烈。
4 结 论
从理论上论证了基于行波分解的泛频响函数法在高承台桩灾后无损检测和评估中应用的可行性,分析了相关参数对检测截面处的泛频响函数及由泛频响函数变换得到的速度时域响应曲线的影响,结果表明:
(1) 承台尺寸的变化对泛频响函数和速度时域响应曲线完全没有影响,上部结构被很好地隔离。
(2) 桩侧土和桩底土剪切波速的变化只是改变了信号能量的耗散程度,而不会改变泛频响函数曲线及速度时域响应曲线所包含的检测截面以下的桩长信息。
(3) 桩身缺陷对泛频响函数影响较大,缺陷的位置和严重程度在速度时域响应曲线内可以明显地反映出来。
需要指出的是,本文采用黏弹性支撑边界模拟承台对桩顶的作用,虽然与实际情况存在一定偏差,但本文证明了泛频响函数法能够将上部结构很好地隔离开来,为建立一种新的检测分析方法提供了重要的理论依据。泛频响函数法使得高承台桩的无损检测工作变得简单易行,具有广阔的应用前景,值得进行更为深入的研究。
[1] 徐攸在,刘家林,刘杰.用小应变动测法测定码头桩完整性的初步探讨[J].港工技术,2001,34(8):36-37.
XU Youzai, LIU Jialin, LIU Jie. Preliminary investigation of integrity testing of pier piles by low-strain dynamic method[J]. Port Engineering Technology, 2001,34(8): 36-37.
[2] 孙熙平,王元战,徐满意,等.高桩码头基桩完整性检测技术研究综述[J].港工技术,2010,47(2):50-53.
SUN Xiping, WANG Yuanzhan, XU Manyi, et al. Research summary of integrity detection for high-piled wharf pile[J]. Port Engineering Technology, 2010, 47(2): 50-53.
[3] 孙熙平,王元战,徐满意,等.应力波在高桩码头基桩中传播数值模拟研究[J].港工技术,2010,47(4):26-28.
SUN Xiping, WANG Yuanzhan, XU Manyi, et al. Numerical research of wave propagation in foundation pile of high-piled wharf[J]. Port Engineering Technology, 2010, 47(4): 26-28.
[4] 柴华友, 刘明贵, 白世伟, 等.应力波在承台-桩系统中传播数值分析[J].岩土工程学报,2003,25(5):624-628.
CHAI Huayou, LIU Minggui, BAI Shiwei, et al. Numerical analysis of wave propagation in platform-pile system[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5): 624-628.
[5] 柴华友,刘明贵,李祺,等.应力波在平台-桩系统中传播的实验研究[J].岩土力学,2002,23(4):459-464.
CHAI Huayou, LIU Minggui, LI Qi, et al. Propagation of stress waves in a plate-pile system: experimental studies[J]. Rock and Soil Mechanics, 2002, 23(4): 459-464.
[6] ADDISON P S, SIBBALD A, WATSON J N. Wavelet analysis: a mathematical microscope with civil engineering applications[J]. Insight-Non-Destructive Testing and Condition Monitoring,1997, 39(7): 493-497.
[7] ADDISON P S, WATSON J N. Wavelet analysis for low-strain integrity testing of foundation piles[C]∥Proceedings of the 5th International Conference on Inspection, Appraisal, Repairs, Maintenance of Buildings and Structures. [S.l.]:[s.n.], 1997: 15-16.
[8] NI S H, LO K F, LEHMANN L, et al. Time-frequency analyses of pile-integrity testing using wavelet transform [J]. Computers and Geotechnics, 2008, 35(4): 600-607.
[9] HARTUNG M, MEIER K, RODATZ W. Integrity testing on model pile[C]∥Proceedings of the 4th international conference on the application of stress-wave theory to piles. Rotterdam:[s.n], 1992: 265-271.
[10] LO K F, NI S H, HUANG Y H. Non-destructive test for pile beneath bridge in the time, frequency, and time-frequency domains using transient loading[J]. Nonlinear Dynamic, 2010, 62(1): 349-361.
[11] GASSMAN S L, FINNO R J. Cutoff frequencies for impulse response tests of existing foundation[J]. Journal of Performance of Constructed Facilities, 2000, 14(1): 11-21.
[12] DAVIS A G. Nondestructive evaluation of existing deep foundations[J]. Journal of Performance of Constructed Facilities, 1995, 9(1): 57-74.
[13] DAVIS A G, EVANS J G, HERTLEIN B H. Nondestructive evaluation of concrete radioactive waste tanks[J]. Journal of Performance of Constructed Facilities, ASCE, 1997, 11(11): 161-167.
[14] FINNO R J, OSBORN P W. Parallel seismic evaluation of the NDE test section at the national geotechnical experimentation site at northwestern university[R]. [S.l.]: The Infrastructure Technology Institute, Northwestern University, 1997.
[15] NI S H, HUANG Y H, ZHOU X M, et al. Inclination correction of the parallel seismic test for pile length detection[J]. Computers and Geotechnics, 2011, 38(2): 127-132.
[16] HUANG D Z, CHEN L Z. Studies on parallel seismic testing for integrity of cemented soil columns[J]. Journal of Zhejiang University SCIENCE A, 2007, 8(11): 1746-1953.
[17] HUANG D Z, CHEN L Z. 3D finite element analysis of parallel seismic testing for integrity evaluation of in-service piles[C]∥Innovative Applications of Geophysics in Civil Engineering.[S.l.]:ASCE, 2007.
[18] LIAO S T, TONG J H, CHEN C H, et al. Numerical simulation and experimental study of parallel seismic test for piles[J]. International Journal of Solids and Structures, 2006, 43(7/8): 2279-2298.
[19] 陈龙珠,赵荣欣. 旁孔透射法确定桩底深度计算方法评价[J].地下空间与工程学报,2010,6(1): 157-161.
CHEN Longzhu, ZHAO Rongxin. On determination of pile length with parallel seismic testing for existing structures[J]. Chinese Journal of Underground Space and Engineering, 2010,6(1): 157-161.
[20] 杜烨,陈龙珠,马晔,等. 旁孔透射法确定桩底深度方法的有限元分析[J]. 防灾减灾工程学报,2012,32(6): 731-736.
DU Ye, CHEN Longzhu, MA Ye, et al. Determination of pile length using parallel seismic testing with FEM simulation[J]. Chinese Journal of Disaster Prevention and Mitigation Engineering, 2012,32(6): 731-736.
[21] 黄大治,陈龙珠.旁孔透射法检测水泥搅拌桩的三维有限元分析[J]. 上海交通大学学报,2007,41(6): 960-964.
HANG Dazhi, CHEN Longzhu. 3D finite element analysis of parallel seismic method for integrity of cemented soil columns[J]. Journal of Shanghai Jiaotong University, 2007,41(6): 960-964.
[22] 黄大治,陈龙珠.旁孔透射波法检测既有建筑物的三维有限元分析[J].岩土力学,2008,29(6):1569-1574.
HUANG Dazhi, CHEN Longzhu. 3D finite element analysis of parallel seismic tests for integrity of piles of existing structures[J]. Rock and Soil mechanics, 2008, 29(6): 1569-1574.
[23] RANDOLPH M F, DEEKS A J. Dynamic and atatic aoil modes for axial pile response[C]//Proceedings of the 4th International Conference on the Application of Stress Wave Theory to Piles. Hague: [s.n.], 1992: 21-24.
Applicationoftheuniversalfrequencyresponsefunctionmethodbasedontravelingwavedecompositioninthenondestructivetestingandassessmentofpost-disastertallplatformpilefoundations
LI Zhenya1, WANG Kuihua1, WU Wenbing2
(1. Research Center of Coastal Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;2. School of Engineering, China University of Geosciences, Wuhan 430074, China)
The universal frequency response function method based on traveling wave decomposition was put forward aiming at the limitation of existing methods in the nondestructive testing and assessment of post-disaster tall platform pile foundations. The reaction of the pile cap on the pile head was simplified as a complex impedance, and the universal frequency response function at the test section was calculated according to the wave equation analysis. Then, the information contained in the universal frequency response function was switched from the frequency domain to the time domain by virtually applying a half-sine pulse at the test section. As a result, the time domain response curve of the virtually isolated single pile below the test section was obtained. Finally, a parametric study was undertaken to investigate the influences of pile-soil parameters on the universal frequency response function as well as the time domain response transformed from it. The results show that the method proposed can completely eliminate the influence of the superstructure, which simplifies the testing procedure and reduces the difficulty of analysis.
gridge engineering; nondestructive test; universal frequency response function; tall platform pile; traveling wave decomposition; wave equation analysis
TU473
A
10.13465/j.cnki.jvs.2017.19.004
国家自然科学基金面上项目(51378464; 51579217;51309207)
2016-02-24 修改稿收到日期:2016-07-20
李振亚 男,博士生,1989年生
王奎华 男,博士后,教授,博士生导师,1965年生
