冲击振动单边单质量破碎系统的非线性动力学分析

倪素环，杨 雪

(河北科技大学机械工程学院，河北石家庄 050018)

1008-1542(2017)05-0469-05

10.7535/hbkd.2017yx05009

冲击振动单边单质量破碎系统的非线性动力学分析

倪素环，杨 雪

(河北科技大学机械工程学院，河北石家庄 050018)

为研究和开发高效振动式破碎机，针对所研究的冲击振动破碎系统建立单边动力学模型，利用牛顿定律建立振动微分方程，进行动力学分析。通过作出幅频曲线、滞回冲击力曲线、能量吸收曲线，分析其对系统响应的影响。利用所得结论用数值分析法解出此系统受迫主共振，求得位移、速度及加速度的时间历程，说明质量块的运动并非简单的简谐运动，非线性冲击力是振动系统中影响较大的一个因素；得到间隙、激振频率对幅频曲线、冲击力和能量吸收的影响规律。研究表明，物料与破碎头之间的间隙值应尽量小，以用更小的激振力达到更好的破碎效果，且系统工作在主共振区时可获得大的冲击力。研究结果为深入分析振动系统的规律及机制提供了参考。

矿石处理；单边单质量；幅频；冲击力；能量吸收；动力学

所谓振动破碎是指由相对振动的2个刚体，对其间的颗粒层加以高频冲击，使层间发生破碎[21]。如图1所示破碎机具有6个自由度，是一个具备刚体复杂运动的振动系统，此系统同时具有强非线性刚-散耦合特性[1-7]。在此振动系统中，研究刚-散耦合效应，势必对其规律及机制进行深入的研究分析。故首先研究冲击振动系统中单边单质量系统。

1 建立动力学模型

对图1所示的破碎系统建立动力学模型，2个偏心距为e的相同偏心块(质量分别为m0/2)连接在弹性梁上，每个电机驱动1个偏心块，让2台电机以相同的角速度ω反方向转动，产生的离心力为m0eω2sin(ωt)，则系统产生图2所示x方向的强迫振动，位于偏心块下部的冲击破碎头会撞击物料槽中的物体使其破碎。如图2所示为其动力学模型，比例阻尼c和线性弹簧k与质量块m三者相连，系统在激振力m0eω2sin(ωt)的作用下做强迫振动，当x大于σ时，质量块就会撞击物料，使其破碎。假设在振动过程中，弹簧产生线性恢复力，物料产生冲击恢复力，而该冲击恢复力以一种非线性、非光滑形式出现[2]。

图1 冲击振动单质量破碎系统Fig.1 Single mass vibration impacting crashing system

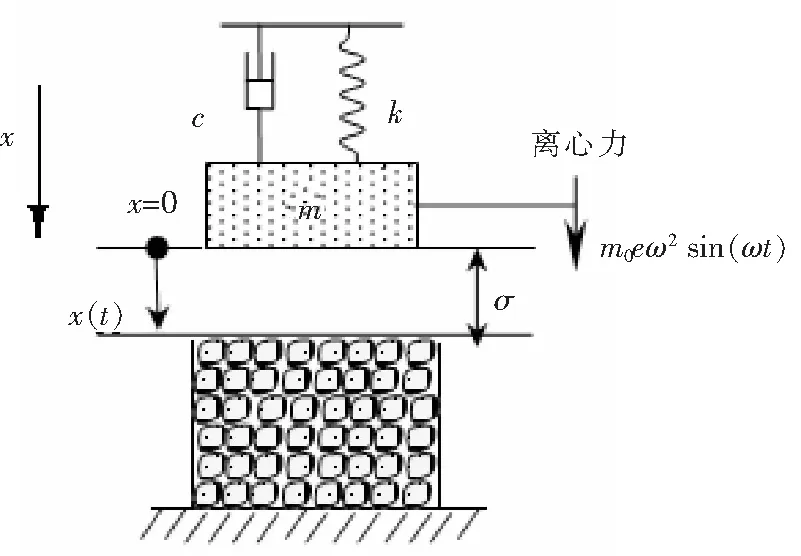
图2 动力学模型Fig.2 Dynamic model

2 振动微分方程

首先建立坐标系，坐标原点为静平衡位置，横坐标为x，向下为正，如式(1)所示，利用牛顿定律建立振动微分方程。

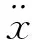
其中

式(1)可规范为

首先要将二阶微分方程化为状态方程形式，引入状态变量：

状态变量y1和y2分别代表质量块的绝对位移和绝对速度，因而可以写出状态方程组如式(4)所示。

分段表示的系统状态方程如下。

1)当y1≥σ且y2≥0时

3)当y1<σ时

给定系统参数，选择合适的步长，就可以利用Runge-Kutta法对系统进行数值分析[9-11]。

3 动力学分析

设式(1)中的参数为

m=135 kg,m0=17.57 kg,e=0.032 6 m,k=2.115 31×105N/m,ξ=0.06，a4=8.378 7×1011,a3=-0.151 4×1011,a2=0.001 9×1011,a1=0.0,a0=0.0,b1=5.606 5×107,b0=-0.107 9×107。

针对式(1)用荣格库塔(Runge-Kutta)4阶法进行数值求解，研究此系统运动的规律。

图3 幅频曲线Fig.3 Amplitude frequency diagram

3.1 影响系统响应的间隙、频率比

3.1.1 幅频曲线

作不同间隙值σ的幅频曲线，如图3所示(频率比λ为横坐标，振幅X为纵坐标)。通过计算得知，当破碎系统中没有物料时，系统的振幅为35 mm,所以当σ≥35 mm时，质量块不会与物料产生接触，系统的振动就不会受到系统内物料的影响。由图3可知：

1)系统的主共振频率与物料的间隙量密切相关，间隙量越小，主共振频率就越大。

2)系统在σ=0～3.2 mm的范围内，只产生了1/2次亚谐共振，没有出现其他亚谐共振。

图4 冲击力曲线Fig.4 Wallop diagram

3)系统的主共振幅值与物料的间隙量也密切相关，间隙愈小，系统的振动幅值愈小。

3.1.2 冲击力曲线

如图4所示为不同间隙值σ下的冲击力曲线(频率比λ为横坐标，冲击力的最大值f为纵坐标)。

由图4可知：

1)当间隙不变时，冲击力在主共振点达到最大值，越过主共振点，冲击力迅速减小；冲击力在1/2次亚谐共振点再次达到峰值。故在主共振点或亚谐共振点冲击力较大。

2)当频率比不变时，冲击力随间隙的增大而减小，直至趋于零。

3)冲击力存在的频率范围受间隙影响，间隙越小，频率范围越大。

所以，物料与破碎头之间的间隙要小，才能用小的激振力达到好的破碎效果，且系统最好在主共振区或亚谐共振区工作以获得大的冲击力。

图5 能量吸收曲线Fig.5 Energy absorbing diagram

3.1.3 能量吸收曲线

破碎效果最重要的因素是能量吸收，作不同间隙值σ的能量吸收曲线，如图5所示(频率比λ为横坐标，能量吸收E为纵坐标)。由图5可知：

1)能量吸收的效果受间隙影响，间隙愈小，能量吸收反而愈大。

2)能量吸收在主共振时最大，亚谐共振时较小。

3)在主共振时物料每个周期被冲击1次，在1/2次亚谐共振时物料每2个周期被冲击1次，由此可知，在相同时间内，能量吸收在主共振点时最大。

3.2 系统的受迫主共振

分析间隙为零的情况，从图3的幅频曲线得出，当σ=0时，共振频率比λ=1.3，用数值仿真法对系统的共振情况进行分析，得到位移、速度和加速度的时间历程图，如图6—图8所示。

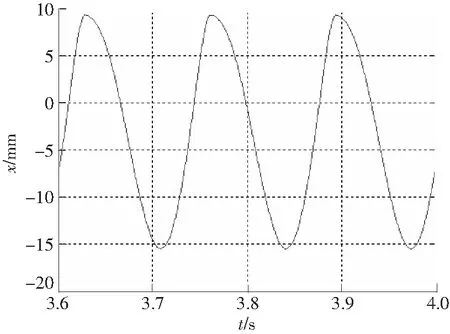
图6 位移历程Fig.6 Displacement course

图7 速度历程Fig.7 Speed course

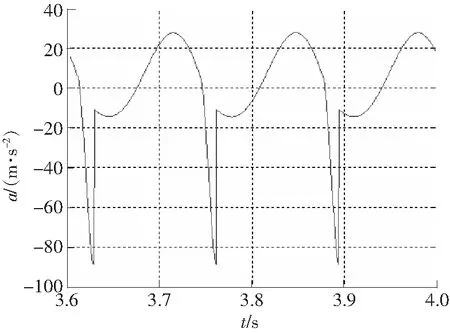
图8 加速度历程Fig.8 Acceleration course

由图6—图8可知：

1)位移历程的正向幅值小于负向幅值，是非对称的。图6显示当正向幅值是9.3 mm时，负向幅值是-15.5 mm。

2)速度历程形状与简谐波发生了很大变化，也是非对称的，正向峰值大于负向峰值，且速度在正向冲击时达到峰值的时间较短，在负向返回时达到峰值的时间较长。

3)加速度历程有一狭窄峰值，当冲击发生时，加速度突然增大但时间很短。

4)由于位移、速度、加速度历程与典型间歇运动曲线有很大不同，故质量块的运动并不是简单的简谐运动，其非线性冲击力是较大影响因素。

4 结 论

应用荣格库塔(Runge-Kutta)4阶法对单边单质量冲击振动破碎系统进行数值计算和分析得出以下结论：

1)非线性冲击力是振动系统中影响较大的一个因素，且质量块的运动并非简单的简谐运动。

2)幅频曲线、冲击力曲线和能量吸收曲线受间隙、激振频率影响的规律，为振动破碎工艺的设计提供了参考——应尽可能让物料与破碎头之间的间隙值小，这样就能用更小的激振力达到更好的破碎效果，且系统最好工作在主共振区以获得大的冲击力。

本文只针对大颗粒物料进行了研究，小颗粒物料振动系统的振动性态更为复杂，需进一步深入研究。

/

[1] 倪素环. 振动辊式破碎机破碎过程的非线性动力学分析[D].秦皇岛：燕山大学，2006.

NI Suhuan.The Nonlinear Dynamics Analysis of the Crushing Process of the Vibrating Roller Crusher[D].Qinhuangdao: Yanshan University,2006.

[2] 倪素环,陈青果.颗粒层受压破碎过程的试验研究[J].金属矿山，2011(1)：109-112.

NI Suhuan,CHEN Qingguo.Experimental studying on granular material compression crushing[J].Metal Mine,2011(1)：109-112.

[3] 朱海东.单质量双边冲击振动破碎系统非线性动力学分析[J].甘肃科技，2011，27(2)：36-37.

ZHU Haidong.The nonlionar dynamics analysis on vibration-impact crushing system of a bilateral single-mass[J]. Gansu Science and Technology,2011,27(2):36-37.

[4] 赵月静,彭伟,侯书军,等.振动圆锥破碎机的动力学响应分析[J].河北科技大学学报,2006,27(3):230-233.

ZHAO Yuejing,PENG Wei,HOU Shujun,et al.Dynamics equations analysis of the vibration-cone-crusher[J].Journal of Hebei University of Science and Technology,2006,27(3):230-233.

[5] 熊洋,蔡改贫,夏刘洋,等.振动破碎机试验与工作参数优化分析[J].有色金属(选矿部分)，2015(5)：56-59.

XIONG Yang,CAI Gaipin,XIA Liuyang,et al.Vibration crusher test and work parameter optimization analysis[J].Nonferrous Metals(Mineral Processing Section),2015(5):56-59.

[6] 戴德成.非线性振动[M].南京：东南大学出版社,1992:7-14.

[7] 侯书军.双质体线性振动系统的动力学研究[J].河北科技大学学报,2003,24(2):1-4.

HOU Shujun.Dynamic research on linear vibration system of double mass[J].Journal of Heber University of Science and Technology， 2003，24(2):1-4.

[8] 王旭,刘方明,张以哲.基于惯性振动破碎技术实现物料细碎的研究[J].有色金属(选矿部分)，2016(3)：66-71.

WANG Xu,LIU Fangming,ZHANG Yizhe.Research on materials fine crushing based on inertia vibrating crushing technology[J].Nonferrous Metals(Mineral Processing Section)，2016(3)：66-71.

[9] 刘树英，韩清凯，闻邦椿.新型振动破碎机非线性动力学分析[J].振动与冲击,2000，19(3)：34-36.

LIU Shuying,HAN Qingkai,WEN Bangchun. The nonlionar dynamics analysis of the new vibrating crusher[J]. Journal of Vibration and Shock，2000,19(3):34-36.

[10] 张军翠，王立成，侯书军.振动冲击破碎系统的非线性动力学分析[J].矿山机械，2007(10)：51-54.

ZHANG Juncui,WANG Licheng,HOU Shujun.The nonlionar dynamics analysis on vibration-impact crushing system[J]. Mining machi-nery,2007(10)：51-54.

[11] 侯书军,张跃军,陈予恕.惯性振动破碎机的动力学分析[C]// 全国振动与波的利用学术会议.沈阳:东北大学出版社,2000:55-59.

[12] 刘剑飞,胡时胜,胡元育,等.花岗岩的动态压缩实验和力学性能研究[J].岩石力学与工程学报，2000,19(5):618-621.

LIU Jianfei,HU Shisheng,HU Yuanyu,et al.Dynamic compression experiment and mechanical properties of granite[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(5):618-621.

[13] 韩清凯,刘杰, 闻邦椿.不对称滞回模型的一般形式及其参数慢变特性[J].振动与冲击,2000,19(3):14-17.

HAN Qingkai,LIU Jie,WEN Bangchun.Asymmterical hysteretic model of general type and the parameters are slow to change[J].Journal of Vibration and Shock,2000,19(3):14-17.

[14] 韩清凯, 闻邦椿.一种不对称滞回受迫振动系统及其分析[J].振动工程学报,1998,11(3):291-297.

HAN Qingkai,WEN Bangchun.An asymmetric hysteresis vibration system and its analysis[J].Journal of Vibration Engineering,1998,11(3):291-297.

[15] LACARBONARA W, VESTRONI F. Nonclassical responses of oscillators with hysteretic[J]. Nolinear Dynamics, 2003, 32:235-258.

[16] ABRAHAM I T, JEE A C. Approximate asymptotics for a nonlinear mathieu equation using harmonic balance based averaging[J]. Nonlinear Dynamics, 2003,31:347-365.

[17] DAS L, JEE A C. Multiple scales via galerkin projections:approximate asymptotics for strongly nonlinear oscillations[J]. Nonlinear Dynamics, 2003,32:161-186.

[18] ZHANG Aimin, LIU Qiaoling, WEN Bangchunn. Dynamic research of a nonlinear stochastic vibratory machine[J]. Shock and Vibration, 2002,9:277-281.

[19] BABITSKY V I. Theory of Vibro-Impact System and Application[M]. Berlin: Springer-Verlag, 1998:103-125.

[20] 闻邦春，刘凤翅.振动机械的理论及应用[M].北京 :机械工业出版社，1980:240-253.

[21] 魏海燕,闻邦椿.惯性圆锥破碎机的非线性动力学特性研究[C]//全国振动与波的利用学术会议.沈阳:东北大学出版社，2000:60-63.

Nonlinear dynamic analysis of single-sided & single-mass crushing system under impact and vibration

NI Suhuan， YANG Xue

(School of Mechanical Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018,China)

To research and develop efficient vibrating type crusher, a single-sided dynamic model is established for the impact and vibration crushing system, and the differential equation of vibration is set up with Newton's law for dynamic analysis. By making amplitude frequency curve, hysteretic impact force curve and energy absorption curve, the influence of which on the system response is analyzed. Based on the conclusion and using numerical method, the primary forced resonance of the system is calculated, and the time history of displacement, velocity and acceleration is obtained, showing that the motion mass movement is not a simple harmonic motion, the nonlinear impact force is one of the factors that influences the vibration system, and the influence rules of clearance, vibration frequency on the amplitude frequency curve, impact force and energy absorption are also obtained. The gap between the material and the broken head should be kept as small as possible so as to achieve a better crushing effect with a smaller excitation force, and the system is best to work in the main resonant area to get a big impact. The research result provides reference for further study of rules and mechanism of the vibration systems.

ore processing; single -sided & single- mass; amplitude frequency; impact force; energy absorption; dynamics

TH113.1

A

2017-07-01；

2017-08-25；责任编辑：冯 民

倪素环(1971—)，女，河北石家庄人，讲师，硕士，主要从事机电专业方面的教学与研究。

E-mail:suhuan-ni@126.com

倪素环，杨 雪.冲击振动单边单质量破碎系统的非线性动力学分析[J].河北科技大学学报,2017,38(5):469-473.

NI Suhuan，YANG Xue.Nonlinear dynamic analysis of single-sided & single-mass crushing system under impact and vibration[J].Journal of Hebei University of Science and Technology,2017,38(5):469-473.