空间冗余机械臂的路径规划算法研究
2017-11-04裴甲瑞陆智俊吴敬玉陈秀梅
陈 撼,裴甲瑞,陆智俊,吴敬玉,陈秀梅
(上海航天控制技术研究所,上海 201109)
空间冗余机械臂的路径规划算法研究
陈 撼,裴甲瑞,陆智俊,吴敬玉,陈秀梅
(上海航天控制技术研究所,上海 201109)
对空间机械臂的路径规划算法进行了研究。针对一种星体和冗余机械臂(7自由度)的星臂联合系统,采用星臂联合路径规划方法。建立了机械臂末端位置和姿态的运动学方程。用基于多项式的伪逆路径规划算法对路径进行规划。仿真发现用三次多项式规划算法所得系统运行平滑且稳定末端能跟踪上目标,运行初始和结束时刻角速度达到设计要求,但系统运行结束时角加速度未收敛至零,存在软冲击缺陷。增加两个角加速度约束条件,用五次多项式改进了规划算法,仿真发现该系统解决了软冲击问题,且运行更稳定。为避免伪逆算法因奇异而失效的固有问题,设计了一种基于五次多项式的伪逆路径和规避奇异路径的联合规划方法。采用倒数法规避奇异问题,当奇异出现时,采用规避奇异路径规划算法,计算阻尼最小方差广义逆矩阵;当奇异不出现时,采用基于五次多项式的路径规划算法,计算雅可比矩阵的广义逆。最后可规划出机械臂各关节的角速度。仿真表明:用该联合规划方法所得系统在保证运行的精度和稳定度的同时,可避免奇异问题,提供了系统的稳定性和安全性。研究对空间机械臂设计有一定的参考价值。
空间冗余机械臂; 路径规划; 动力学耦合; 软冲击; 奇异; 伪逆路径规划算法; 规避奇异路径规划算法; 五次多项式
0 引言
随着空间技术的进步,全球发射的卫星和航天器数量不断增多,随之而来的是空间工作的多样性和复杂性迅速增长,对舱外活动的需求也日益增加,如对在轨航天器的抓捕、维修和燃料补充,外空间环境的科学试验,以及空间垃圾的清理等[1-3]。根据国际空间站的搭建和维护经验,利用空间机械臂辅助航天员完成空间搭建和载荷维护等任务,可明显减小航天员出舱风险,减轻航天员的工作压力,提高空间探索活动的效率[4]。近年来,各航天大国均投入巨资竞相开展航天器在轨操控技术研究[5-6]。实践证明,空间机械臂是一种非常有效的完成在轨操控任务的手段,特别适于对操控精度要求较高的空间精细操控。
动力学建模、路径规划和控制技术是机械臂在轨操控的三大核心技术[7-8]。本文研究了空间机械臂的路径规划技术,并重点解决两大问题:一是在空间微重力环境中,动量守恒的约束使机械臂与星体间存在动力学耦合问题;二是基于多项式的伪逆路径规划算法的固有缺陷导致的奇异问题[9]。对此,本文分别设计了星臂联合路径规划方法(即将星体和冗余机械臂(7自由度)结合成一个系统,进行联合建模)和常规路径规划算法与规避奇异规划算法的联合路径规划方法[10]。同时,针对系统软性冲击的问题提出了基于五次多项式的伪逆路径规划算法,并进行了仿真验证。
1 空间机械臂数学模型
本文研究的是对象是星体和冗余机械臂(7自由度)组成的星臂联合系统,如图1所示。采用星臂联合路径规划方法,可有效解决机械臂与星体间存在的动力学耦合问题,同时避免了数学模型因增加解决耦合问题的算法而带来的复杂度,而且增加了系统运行的灵活度(增加了3自由度),丰富了系统的运行轨迹。同时,该方法能大量节约由于抵消机械臂运行对星体产生的扰动而消耗的燃料。
建立该系统的运行学数学模型如下。
a)机械臂末端位置的运动学方程
(1)
式中:q,JL(q)分别为本体与机械臂联合角位移列向量和位置雅克比矩阵,且
q=[φθψθ1θ2…θ7]T
JL(q)=[JL0JL1JL2…JL6JL7]3×10
此处:φ,θ,ψ分别为本体的滚动角、俯仰角和偏航角;θi(i=0~7)为机械臂的关节角;
JL1=-(AI1(r12)×+AI2(r23)×A21+AI3(r34)×A31+AI4(r45)×A41+AI5(r56)×A51+AI6(r67)×A61+AI7(rt)×A71)Γ1
JL2=-(AI2(r23)×+AI3(r34)×A32+AI4(r45)×A42+AI5(r56)×A52+AI6(r67)×A62+AI7(rt)×A72)Γ2
JL3=-(AI3(r34)×+AI4(r45)×A43+AI5(r56)×A53+AI6(r67)×A63+AI7(rt)×A73)Γ3
JL4=-(AI4(r45)×+AI5(r56)×A54+AI6(r67)×A64+AI7(rt)×A74)Γ4
JL5=-(AI5(r56)×+AI6(r67)×A65+AI7(rt)×A75)Γ5
JL6=-(AI6(r67)×+AI7(rt)×A76)Γ6
JL7=-(AI7(rt)×)Γ7
此处:Aij为第j节机械臂相对第i节机械臂固联坐标系的转换矩阵;AIb为本体系相对惯性系的转换矩阵;AIi为第i节机械臂相对惯性系的转换矩阵;rij为第j节机械臂固联坐标系原点相对第i节的位移;上标“×”表示叉乘斜对称矩阵;Γj为投影矩阵,其取值为[1 0 0]T,[0 1 0]T或[0 0 1]T,与坐标系选取有关。
b)机械臂末端姿态的运动学方程
将式(1)写为矩阵形式
(2)
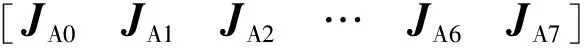
JA0=AI7(et)×A7b
JA1=AI7(et)×A71Γ1
JA2=AI7(et)×A72Γ2
JA3=AI7(et)×A73Γ3
JA4=AI7(et)×A74Γ4
JA5=AI7(et)×A75Γ5
JA6=AI7(et)×A76Γ6
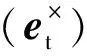
此处:A7b为本体系相对第7节机械臂的转换矩阵。
2 基于多项式的伪逆路径规划方法
采用基于多项式的伪逆路径规划算法。该算法是通过机械臂末端位姿变化相对本体的姿态及机械臂关节角速率间的关系建立的基于广义雅可比矩阵的逆轨迹规划,可对目标的相对运动进行反馈补偿,能实时对运动进行精细的调整与控制,具精度高的优点。
为使运动较平缓,不出现剧烈的变化,可设计一个二阶连续光滑的函数,并使之满足上述约束条件即可。一般可用圆弧函数、多项式函数、三角函数或样条插值函数等,本文采用多项式函数[11]。
设初始时刻为t0,末端参考点相对惯性坐标系原点的位置为rtI0,终止时刻为tf,末端参考点相对位置为rtIf。则对所要设计的位置运动规律rtI(t)来说,需满足初始时刻和终止时刻的位置,速度的约束条件,即
rtI(tf)=rtIf
本文采用三阶多项式,得到末端位置的运动规律为
(3)
式中:t为时刻。
设计姿态运动律时,考虑参考矢量的方位角e(t),设初始时刻t0时的值为e0,终止时刻tf时的值为ef,则由与位置运动规律类似的方法,可得姿态运动的变化规律为
(4)
为实现对机械臂末端的位置和姿态运动的联合控制,需给出机械臂末端运动的位置姿态联合方程。定义位置姿态联合矢量为XE,XE=[rtIetI]T。
合并式(3)、(4),有
(5)
式中:J(q)为雅克比矩阵,且
J(q)=[JL(q)JA(q)]T
求解各关节角的运动规律,须对J求逆,但J不为方阵,不一定可逆,故需用J的Moore-Pseudo广义逆矩阵进行计算[12-13]。根据时刻t的q(t)求解矩阵J(q),并进而求解J的广义逆矩阵J+。其求解结果为
J+=JT(J·JT)-1
(6)
另由式(5)可得
(7)
将式(6)求出的J+和前文获得的位置姿态矢量的变化规律XE(t)代入式(8)即可求出各关节角的角速度变化规律。
用本文的路径规划算法进行数值仿真。选择一个3-1-3(肩、肘、腕)构型的关节型机械臂作为仿真目标,该机械臂的最大臂展长度1.1 m。机械臂的空间构型和机械臂的参数分别如图2、3所示。
用本文的路径规划算法仿真所得航天器本体和机械臂各关节角的姿态角、角速度、角加速度结果分别如图4~9所示。
由图4~9可知:系统运行平滑且稳定,且末端跟踪上指定目标,运行初始和结束时的角速度为零,达到预定设计要求,但系统运行结束时的角加速度并未收敛至零,这会对系统产生软冲击,降低星臂联合系统的末端跟踪精度和稳定度,而且会显著缩短电机的使用寿命,甚至会破坏整个系统。因此,需对该系统进行改进,解决该算法的软性冲击缺陷。
对要设计的位置运动规律rtI(t)来说,需满足初始时刻和终止时刻的位置、速度和加速度约束条件
rtI(tf)=rtIf
为使运动更平缓,运动结束时不出现大的角加速度变化,本文采用五次多项式进行参数化处理的方法,则末端位置的运动规律为


(8)
同样,用与位置运动规律完全类似的方法,可得末端姿态的运动规律为

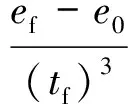
(9)
用本文的改进规划算法仿真所得航天器本体和机械臂各关节角的姿态角、角速度、角加速度结果分别如图10~15所示。
由图10~15可知:改进后的系统本体姿态角和机械臂关节角、角速度与角加速度在运行开始和结束时都收敛至0。在不影响基于多项式的伪逆路径规划算法条件下,彻底解决了软冲击的缺陷问题,在提高系统的末端跟踪精度、稳定度的同时解决了系统的潜在风险。用该改进方法设计仿真的角度,角速度和角加速度的结果显示:曲线更平滑,明显降低了电机负荷,又提高了系统的运行稳定性。同时,该算法只增加了两个约束方程,并未增加算法的复杂度,不影响整个系统的运行。但伪逆算法的固有缺陷(J·JT奇异的问题),一旦系统运行至奇异区,会导致该算法失效,因此需设计一个规避奇异的方法进行改进。
3 规避奇异的联合路径规划方法
基于运动学的算法,将机械臂末端的位置和姿态变化路径通过雅可比矩阵的伪逆转换为航天器本体姿态及机械臂各关节角的运行路径过程中,有时会遇到矩阵J·JT接近奇异的情况,此时雅可比矩阵的伪逆无法求解,或所得的角速度幅值很大,导致路径规划算法的失效。这个固有缺陷限制了该算法的应用。因此,需用规避奇异的路径规划方法解决此问题。本文用阻尼倒数法规避奇异问题,其原理是:在J·JT接近奇异值(J·JT的模值等于或接近于0)时,该矩阵的广义逆矩阵J+=Jt(J·JT)-1会出现无限大的值,设计对倒数添加一阻尼系数,在所给系统精度损失的可控范围内使系统快速脱离奇异区间。
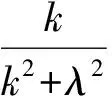
(10)
阻尼倒数(取λ=0.1)与倒数比较(k=1~10)如图16所示。
由图16可知:当设计的阻尼系数相对系数k的绝对值很小时,阻尼倒数能保证近似等于系数的倒数。针对多自由度的机械臂系统的规避奇异路径规划算法,即为对雅可比矩阵的J+进行修改(即阻尼最小方差广义逆矩阵),有
J+=JT(J·JT+λ2I)-1
(11)
式中:I为单位阵。将式(11)代入式(7)可得
(12)
由上述分析可知:阻尼倒数能保证一定的精度条件,但无法避免误差;基于五次多项式的路径规划算法不能规避奇异。为解决该问题,可联合基于五次多项式的路径规划算法与规避奇异路径规划方法,具体为:设计λ=0.1,系统正常运行(J·JT的模值较大,取≥4)时,为保证精度,采用基于五次多项式的路径规划算法;当J·JT发生奇异或接近奇异(即J·JT的模等于0或极小值)时,则切换为规避奇异路径规划方法。联合路径规划方法的流程如图17所示。
用联合路径规划方法仿真所得航天器本体和机械臂各关节角的姿态角、角速度、角加速度结果分别如图18~23所示。
由图18~23可知:系统各关节角的角度、角速度和角加速度变化曲线平滑且稳定,在奇异区间并未出现突变或极大值的现象。分析可知:规避奇异的联合路径规划方法在能保证系统运行的精度和稳定度的同时,解决了伪逆路径规划方法奇异的固有缺陷,提高了系统的稳定性和安全性。
4 结束语
本文设计了星臂联合路径规划方法,避免了数学模型因增加解决耦合问题的算法而带来的复杂度的同时,增加了系统运行的灵活度(增加了3自由度),丰富了系统的运行轨迹。同时,该方法能大量节约用于抵消机械臂运动对星体的扰动而消耗的燃料。针对该模型,采用基于多项式的伪逆路径规划算法,该法具有算法简便、运行轨迹平滑等优点,并用仿真进行了验证。根据系统软冲击的缺陷分析,提出了该方法的改进算法,解决了系统软冲击的问题,提高了系统的精度、稳定度。为解决伪逆路径规划算法奇异的缺陷,采用了联合规避奇异路径规划算法,并通过仿真得到验证。路径规划技术是空间机械臂的三大核心技术之一,对在轨捕获、维修、对接等任务有重要的意义。但本文的空间机械臂路径规划过程中,并未实现实时避障、本体姿态零扰动等功能,后续研究将改进算法以实现相应功能。
[1] 吴立成, 孙富春, 孙增析. 空间机器人建模、规划与控制研究现状[J]. 中南大学学报, 2005, 36(1): 18-24.
[2] 张海涛, 唐立才, 张敬鹏, 等. 空间机械臂双臂协调操作路径规划算法[J]. 控制工程, 2015, 22(6): 1028-1032.
[3] EVANS B G, THOMPSON P T, CORAZZA G E, et al. 1945-2010: 65 years of satellite history from early visions to latest missions[J]. Proceedings of the IEEE, 2011, 99(11): 1840-1857.
[4] 刘宏, 蒋再男, 刘业超. 空间机械臂技术发展综述[J]. 载人航天, 2015, 21(5): 435-436.
[5] HIRZINGER G, BRUNNER B, LAMPARIELLO R, et al. Advances in orbital robotics[C]// Proceedings of the IEEE international Conference on Robotics and Automation. San Francisco: IEEE, 2000: 898-907.
[6] WHELAN D A, ADLER E A, WILSON S B. Effecting a revolution in space-based systems[J]. Proceedings of SPIE, The International Society for Optical Engineering, 2000: 48-56.
[7] 王景, 王昊瀛, 刘良栋. 自由飞行空间机器人的运动学建模研究[J]. 航天控制, 1999, 17(1): 6-10.
[8] 葛景华. 双臂空间机器人运动学、动力学及控制[D]. 福州: 福州大学, 2005.
[9] 丁希仑, 战强, 解玉文. 自由漂浮的空间机器人系统的动力学奇异特性分析及其运动规划[J]. 航空学报, 2001, 22(5): 474-477.
[10] 董晓星, 李戈, 刘刚峰, 等. 冗余空间机械臂的运动学和笛卡尔阻抗控制方法[J]. 中国机械工程, 2014, 25(1): 36-37.
[11] 吕燕, 安凯. 空间6R机械臂圆弧轨迹规划及仿真[J]. 上海航天, 2012, 29(6): 63-67.
[12] OPTIMUM G T. Trajectory planning for redundant and hyper redundant manipulators through inverse dynamics[C]// Proceedings of 17th International Conference on Methods and Models in Automation and Robotics. Albuquerque: IEEE, 2012: 27-30.
[13] GASPARETTO A, ZANOTTO V. Optimal trajectory planning for industrial robots[J]. Advances in Engineering Software, 2010, 41: 548-556.
StudyonPathPlanningMethodofSpaceRedundancyManipulatorSystem
CHEN Han, PEI Jia-rui, LU Zhi-jun, WU Jing-yu, CHEN Xiu-mei
(Shanghai Institute of Spacecraft Control Technology, Shanghai 201109, China)
The path planning method of space redundancy manipulator system was studied in this paper. The satellite and manipulator combined path planning was adopted for a satellite and manipulator system with 7 degree of freedom. The kinematics equations of the position and attitude of the manipulator end were established. The path was planned by pseudo-inverse path planning method based on polynomial. The simulation found that the operation of the system planned by cubic polynomial path planning method was smooth and the manipulator end could track the target. The angular velocity met the design requirement at the initial and finishing time. But the angular acceleration would not converge on zero when the system operation was completed, which meant that there was flexible strike. The path planning method was improved by adding two angular constrained conditions based on quintic polynomial. The simulation found that the flexible strike was eliminated and the system planned by the improved path planning method would operate much smoothly. To avoid the failure of pseudo-inverse path planning because of singularity, a new planning method united pseudo-inverse path planning based on quintic polynomial and singularity avoiding planning was designed. The singularity was avoided by reciprocal method. When the singularity appeared, the singularity avoiding path planning was adopted and calculated damp minimum variance generalized inverse matrices. When the singularity did not appear, the pseudo-inverse path planning based on quintic polynomial was adopted and calculated generalized inverse of Jacobian matrix. At last, the angular velocities of each joint of the manipulator were planned. The simulation showed that the system planned by the new united planning method could avoid singularity when the operation accuracy and smooth were guaranteed, which provided the stability and safety of the redundancy space manipulator system. The study has some valuable for the design of the space manipulator system.
space redundancy manipulator system; path planning; dynamic coupling; flexible strike; singularity; pseudo-inverse path planning; singularity avoidance path planning; quintic polynomial
1006-1630(2017)05-0030-10
2016-12-23;
2017-04-10
陈 撼(1991—),男,硕士,主要研究方向为空间飞行器控制。
TP242.3
A
10.19328/j.cnki.1006-1630.2017.05.005
