脉冲星导航系统观测量异常的改进UKF滤波算法研究

姜 宇，李晓宇，金 晶

(哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001)

脉冲星导航系统观测量异常的改进UKF滤波算法研究

姜 宇，李晓宇，金 晶

(哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001)

为减小观测量异常对X射线脉冲星导航系统的影响，提出了一种改进的无迹卡尔曼滤波(MUKF)导航滤波算法。给出了轨道动力学模型和量测模型。针对观测器校准脉冲星方向时因宇宙尘埃影响会发生细微震动而产生短时段的常值误差，设计异常检测函数，可有效判断有无观测量异常发生。当观测量出现异常时，对UKF进行改进，通过调节滤波器增益减小异常观测的影响，进而得到准确的脉冲星导航系统状态估值，改进的滤波算法使整个导航系统具有更强的容错性和稳定性。对UKF，MUKF两种算法在地球近地轨道上进行了实验仿真，结果表明：提出的MUKF滤波算法可有效消除观测量常值偏差对导航系统的影响。

自主导航； 脉冲星导航； 异常观测量； 无迹卡尔曼滤波； 异常检测函数； 滤波器增益； 系统估值

0 引言

X射线脉冲星导航是一种新兴的自主导航技术，具有精度高，不易受干扰等优点，已成为研究热点[1]。脉冲星是一种高速旋转的中子星，可发射具有稳定周期的X射线光子束。X射线光子到达航天器和太阳质心(SSB)的时间差可通过脉冲星计时模型得到并作为导航系统的观测量。再与轨道动力学模型结合，根据EKF，UKF和非线性预测滤波(NPF)等滤波算法得到导航信息[2-7]。但在导航过程中，星体遮挡、导航系统本身星载探测器出现故障，以及外界复杂宇宙环境(太阳活动、星际尘埃)的影响，会使观测量出现零值、噪声过大和常值偏差等异常情况。如单纯利用UKF等滤波算法进行计算，会导致滤波估计误差变大甚至发散，严重影响航天器的定位精度[8-9]。为解决上述问题，本文提出一种针对观测量异常的自适应UKF算法。通过在理论量测残差协方差中加入调节矩阵使理论量测残差与实际量测残差协方差建立等式关系，求出滤波器增益。该方法可有效消除观测量异常对导航系统的影响。与多模型自适应估计算法(MMAE)方法相比，该方法无需增大观测量的维度，有效减少了星载负荷和计算成本，并可有效解决用UKF算法导致导航系统估计误差变大甚至发散的问题，能获得较高的定位精度。

本文对脉冲星导航系统观测量异常时的改进UKF滤波算法进行了研究，给出了脉冲星导航系统的量测模型和轨道动力学模型，引入UKF算法并分析异常观测量对UKF的影响，提出了容错导航方法、异常检测方法及MUKF滤波算法，用实验仿真验证容错导航方法的有效性。

1 X射线脉冲星导航系统模型

1.1轨道动力学模型

在以地球为中心的观测坐标系(J2000.0)中，根据二体运动方程，其轨道动力学模型可表示为

(1)

式中：Re为地球的半径；μe为地球的引力常数；J2为二阶带谐项系数；ΔFx，ΔFy，ΔFz为各种外力作用引起的高阶摄动项在x、y、z三个速度方向的分量，且ΔF=[ΔFxΔFyΔFz]T。航天器导航的状态向量由位置和速度构成，式(1)可简写为

(2)

式中：r，v分别为导航系统在地球惯性坐标系中的位置和速度，且r=[xyz]T，v=[vxvyvz]T。

脉冲星导航系统的轨道动力学模型可简写为

(3)

式中：f(x，t)为航天器运动的速度及受力项；w(x，t)为系统噪声矩阵，且

w(t)=[0 0 0 ΔFxΔFyΔFz]T

1.2量测模型

由脉冲星导航原理可知：脉冲星导航系统的观测量Δt是X射线脉冲星发出的光子到达航天器和SSB的时间差，如图1所示[10]。设RSC为在SSB坐标系中航天器的位置向量，Δt为航天器RSC在第i颗脉冲星方向ni上的投影，则有

(4)

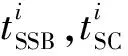
ni=[cosδisinαicosδicosαisinδi]

此处：αi，δi分别为脉冲星在SSB坐标中的赤经和赤纬。则导航系统的量测模型可表示为

yk=h(xk)+Vk

(5)

式中：Vk为系统观测噪声；

h(xk)=[h(1)(xk)h(2)(xk) …h(i)(xk)]T

由式(4)的几何关系可知：h(i)(xk)=niRsc，i为使用脉冲星的数量，本文中取i=3；RSC为航天器相对SSB的位置向量，由坐标转换可得RSC=r+rE。此处：r为航天器相对地球的位置矢量；rE为地球相对SSB的位置，可由JPL提供的DE405星历表预报得到[11]。

式(5)中，Vk表示量测模型的精度，可决定导航系统的性能。脉冲星导航的性能与量测模型精度有关，定义Vk的标准差为

(6)

2 基于UKF算法的脉冲星导航系统

由上，脉冲星导航系统可写为

(7)

式中：wk为系统噪声矩阵。wk，Vk的协方差矩阵分别为Qk，Rk，满足E={wk(wk)T}=Qk，E={Vk(Vk)T}=Rk。用UKF算法对导航系统进行滤波，可得航天的位置信息[12]。UKF算法描述如下。

(8)

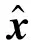
步骤2：预测。每个采样点通过轨道动力学模型f用无迹变换(UT)进行预测，有

χi,k/k-1=f(χi,k-1)

(9)

预测估值及协方差分别为

(10)

Pk/k-1=

(11)

式中：wi为采样点的权重，且

(12)

步骤3：更新。定义量测更新过程为

(13)

(14)

(15)

(16)

Kk=Pxy(Pyy)-1

(17)

(18)

Pk=Pk/k-1-Pxy(Pyy)-1(Pxy)T

(19)

航天器在运行过程中会受到各种因素的影响而不能接收到理论观测模型的观测值，主要有以下情况：航天器在绕飞过程中遭遇星体遮挡或脉冲星导航系统发生紧急故障时，脉冲星的观测信息均会丢失，即观测量为零；受宇宙环境的影响导航系统自身的观测噪声也可能明显增大，使其接收信号的信噪比与理论数学模型相比发生了很大改变；航天器在太阳系中运行时，为获得更高的导航精度，需不断校准航天器与脉冲星的方向信息，但在其运行过程中可能与宇宙尘埃接触发生震动，X射线探测器很难精确校准至脉冲星方向，光子的接收过程出现偏差，导致脉冲星的观测量在一段时间内产生一定的偏差，即整个卡尔曼滤波过程中式(18)的yk产生了常值偏差。本文对最后一种情况进行讨论，定量说明其对整个导航过程的影响。

当观测量yk与真实值出现常值偏差时，UKF滤波算法的定位精度会受影响。导航系统观测量出现常值偏差时用UKF算法进行定位的估计误差如图2所示。假设导航系统在LANDSAT-4轨道进行导航的过程中，在第2.5×105～2.55×105s的时间内脉冲星导航系统的观测量产生了一定偏差，UKF算法的估计误差从20 m急剧增大400 m，导致导航精度变低[13]。

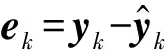
3 导航方法

本文提出一种基于MUKF滤波算法的容错导航方法：根据量测残差设计异常检测函数，判断观测量是否出现异常，当导航系统正常工作时，用UKF算法进行导航计算；当导航系统观测量发生异常时，用MUKF算法修正滤波器增益，得到准确的导航信息。MUKF导航滤波算法的流程如图3所示。

3.1异常检测函数

根据前文用UKF对脉冲星导航系统进行定位的误差分析可知：当导航系统观测量异常时，量测残差ek会增大。因此，本文依据量测残差设计异常检测函数判断当前时刻导航系统是否发生异常并提出两种假设：A0，导航系统观测量正常；A1，导航系统观测量异常。

由对量测残差的分析可知：量测残差序列具正交性，当导航系统观测量未发生异常时，残差序列的均值为零；当导航系统观测量发生异常时，残差序列不再为零。因此，量测残差可作为判断的依据。定义异常检测函数为

(20)

根据χ2分布的定义可知：ηk在统计学上服从自由度为N的χ2分布。此处：N为更新向量的维度。因此，存在α(0<α<1)使

(21)

(22)

(23)

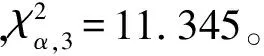
3.2MUKF方法

由于角度校准偏差导致观测量出现常值偏差，而该偏差项yk仅在式(18)中出现，则当UKF滤波算法中的量测残差增大时，可通过调节滤波器增益Kk减小异常观测量对导航系统的影响。观察到Kk项由式(15)、(16)中的Pyy，Pxy组成，本文通过对其中观测误差矩阵Rk进行修正，使实际量测残差协方差与理论值相等，从而使整个系统具一定的鲁棒性。则有

(24)

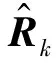
(25)

(26)

(27)

4 仿真

4.1仿真条件

用仿真验证本文MUKF方法的有效性。设航天器绕飞地球轨道LANDSAT-4的轨道参数为：半长轴7 084.62 km；离心率0.000 931；轨道倾角98.086°；升交点赤经81.1123°；近升角距120.320 5°；初始真近点角184.45°[14]。取量测更新时间500 s；所选择的脉冲星参数见表1。令初始误差δx0、初始误差协方差P0，系统噪声协方差Qk，观测噪声协方差Rk分别为

δx0=[900 900 900 3 3 3]TP0=diag[900290029002323232]

Qk=diag[10-810-810-810-1410-1410-14]

Rk=diag[109232523442]

表1 脉冲星参数

对常值误差对导航系统的影响，本文从两个角度进行分析：一是常值误差保持不变而不同观测器失常；二是观测量关系相同但常值误差的幅度不同。

4.2仿真结果分析

在计算机内存CPU 8 GB，Matlab版本(4核，2.5 GHz，R2012b)环境中进行仿真，UKF，MUKF仿真时间分别为39 min 10 s，40 min 50 s。在不同偏差下用UKF，MUKF进行导航的仿真结果如图4～6所示。假设导航系统的观测量在2.5×105～2.55×105s出现常值偏差，其中常值误差的大小为6 km。其中：图4～6对应的观测器异常观测的关系见表2。由图4～6可知：无异常时，用UKF，MUKF两种方法均能获得较好的定位效果，估计误差可稳定在小于50 m；当导航系统在短时间内出现常值偏差时，UKF算法的定位估计误差急剧增大，且估计误差随观测器异常数量增加呈现增大的趋势，而MUKF的定位估计误差仍可稳定地保持小于50 m。

脉冲星情况a情况b情况cB1937+21出现异常出现异常出现异常B1617⁃155正常工作出现异常出现异常J0437⁃4715正常工作正常工作出现异常

轨道在出现观测量异常后估计误差均方根的计算结果见表3。由表3可知：对UKF算法，观测量出现偏差会使滤波器的估计误差结果增大，当3颗脉冲星的观测量同时出现偏差时，估计误差最大，滤波器精度最差，且最高估计误差可达231.16 m；对MUKF算法，导航位置估计误差始可收敛至小于50 m。这表明MUKF滤波算法可有效减小常值偏差对脉冲星导航系统的影响。

表3 两种方法估计误差均方根

当观测器状态相同而偏差幅度不同时，UKF，MUKF导航性能的比较如图7所示。由图7可知：当观测量产生不同程度的偏差时，UKF的估计误差随偏差变大呈增加趋势，而MUKF算法的估计误差仍稳定在50 m以内。这表明，MUKF算法可有效消除观测量常值偏差对导航系统的影响，使观测器校准脉冲星方向更具可靠性和稳定性。

5 结束语

本文分析了观测量异常的可能原因，针对导航系统中观测量出现常值偏差状况提出改进UKF滤波算法，并用于脉冲星导航定位任务。通过分析UKF滤波算法的量测残差设计异常检测函数，对观测量进行判断，并设计相应的观测模型误差调节矩阵，使滤波器的增益项可有效调节量测模型误差的变化。该方法在实际的地球轨道中进行测试并与UKF方法比较。结果表明：本文的MUKF滤波算法可有效减小观测量异常对导航系统的影响，有较高的定位精度。

[1] 帅平, 陈绍龙, 吴一帆, 等. X射线脉冲星导航原理[J]. 宇航学报, 2007, 28(6): 1538-1543.

[2] QIAO L, LIU J Y, ZHENG G L, et al. Augmentation of XNAV system to an ultraviolet sensor-based satellite navigation system[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(5): 777-785.

[3] LIU J, FANG J C, MA X, et al. X-ray pulsar/starlight Doppler integrated navigation for formation flight with ephemerides errors[J]. IEEE Aerospace and Electronic Systems Magazine, 2015, 30(3): 30-39.

[4] LIU J, MA J, TIAN J, et al. X-ray pulsar navigation method for spacecraft with pulsar direction error[J]. Advances in Space Research, 2010, 46(11): 1409-1417.

[5] FENG D, GUO H, WANG X, et al. Autonomous orbit determination and its error analysis for deep space using X-ray pulsar[J]. Aerospace Science and Technology, 2014, 32(1): 35-41.

[6] LIU J, MA J, TIAN J, et al. Pulsar navigation for interplanetary missions using CV model and ASUKF[J]. Advances in Space Research, 2010, 46(11): 1409-1417.

[7] 金晶, 王敏, 黄良伟, 等. NPF算法在X射线脉冲星导航中的应用研究[J]. 宇航学报, 2015, 36(11): 1248-1254.

[8] XIONG K, WEI C, LIU L. Robust multiple model adaptive estimation for spacecraft autonomous navigation[J]. Aerospace Science Technology, 2015, 42: 249-258.

[9] LI S, JIANG X, LIU Y. Innovative Mars entry integrated navigation using modified multiple model adaptive estimation[J]. Aerospace Science and Technology, 2014, 39: 403-413.

[10] EMADZADEH A, SPEYER J. On modeling and pulse phase estimation of X-ray pulsars[J]. IEEE Transactions on Signal Processing, 2010, 58(9): 4484-4495.

[11] STANDISH E M. An approximation to the errors in the planetary ephemerides of the Astronomical Almanac[J]. Astronomy & Astrophysics, 2004, 417(3): 1165-1171.

[12] XIONG K, ZHENG H Y, CHEN C W. Performance evaluation of UKF-based nonlinear filtering[J]. Automatica, 2006, 42(2): 261-270.

[13] WANG Y, ZHENG W, SUN S, et al. X-ray pulsar based navigation using time-differenced measurement[J]. Aerospace Science and Technology, 2014, 36: 27-35.

[14] SOKEN H E, HAJIYEV C, SAKAI S. Robust Kalman filtering for small satellite attitude estimation in the presence of measurement faults[J]. European Journal of Control, 2014, 20(2): 64-72.

ModifiedUnscentedKalmanFilterAlgorithmforXNAVwithAbnormalMeasurement

JIANG Yu， LI Xiao-yu， JIN Jing

(School of Astronautics, Harbin Institute of Technology, Harbin 150001, Heilongjiang, China)

In order to reduce the influence of the fault measurement to the X-ray pulsar based navigation (XNAV), a modified unscented Kalman filter algorithm (MUKF) was proposed in this paper. The orbit dynamic model and measurement model were given. For the problem of X-ray detector would be vibrated slightly due to the impact of cosmic dust which resulting in a short period of constant error, the abnormal detection function was designed which could detect the measurement’s abnormal situation effectively. When the situation of abnormal measurement appeared, the conventional UKF’s filter gain was modified to obtain the XNAV’s state estimation accurately by adjusting the filter gain to reduce the influence of abnormal observations. The proposed method can make the navigation system has more strong fault toreance and stability. The MUKF algorithm was tested on the earth orbit and the corresponding performance was compared with the UKF algorithm. The simulation results showed the MUKF method proposed could greatly reduce the impact the abnormal measurement to X-ray pulsar navigation system.

autonomous navigation; X-ray pulsar based navigation (XNAV); abnormal measurement; unscented Kalman filter; abnormal measurement function; filter gain; system estimation

1006-1630(2017)05-0023-07

2016-12-30；

2017-06-01

上海航天科技创新基金资助(SAST20160024)

姜 宇(1982—)，男，博士，主要研究方向为飞行器自主导航。

V448.224

A

10.19328/j.cnki.1006-1630.2017.05.004