星历模型地月系统平动点拟周期轨道设计研究

刘 刚，黄 静，郭思岩

(1.上海市空间智能控制技术重点实验室,上海 201109； 2.上海航天控制技术研究所,上海 201109)

星历模型地月系统平动点拟周期轨道设计研究

刘 刚1,2，黄 静1,2，郭思岩1,2

(1.上海市空间智能控制技术重点实验室,上海 201109； 2.上海航天控制技术研究所,上海 201109)

为改进使用圆形限制性三体模型设计轨道时缺乏摄动分析的不足，提高轨道设计的精度，对星历模型地月系统平动点拟周期轨道设计方法进行了研究。在不设置假设条件的前提下，考虑月球真实轨道及地球、月球和太阳的影响，在地心J2000惯性坐标系中建立平动点附近航天器高精度的星历模型。以圆形限制性三体中的周期轨道作为迭代初值，用星历表数据对轨道进行拼接获得所需的拟周期轨道；用多步打靶法替代单步微分修正进行迭代，对轨道上各节点进行校正以获得所求的拟周期轨道，给出了轨道设计步骤。仿真结果表明：所提方法可有效获得地月系统平动点附近拟周期轨道，提供满足真实动力学环境的轨道，有效节约轨道保持所需的燃料。该方法有较大的工程应用价值。

地月系统； 平动点； 限制性三体问题； 太阳光压； 引力摄动； 拟周期轨道； 多步打靶法； 星历表

0 引言

平动点是圆形限制性三体问题(CRTBP)中的5个平衡位置，在平动点附近存在大量稳定、不稳定、周期和拟周期运动。平动点附近无残余大气、空间碎片、原子氧等干扰因素的影响，地球红外射线、重力梯度和地球磁场对航天器的影响也非常微弱，非常适于开展各种科学探测任务。因此，对平动点附近轨道设计问题的研究有广泛的应用前景和价值。目前，对平动点附近动力学和轨道设计进行了大量研究。文献[1]用Linstedt-Poincaré(LP)摄动法推导了地月系统L2点附近的周期及拟周期轨道三阶及四阶近似解析解。文献[2]提出了用LP法构建一般Halo轨道的三阶近似解析解的方法，该结果目前仍被用于求解Halo轨道数值计算的初值。随着现代计算机技术的发展，数值计算方法被广泛用于周期轨道的求解，极大地促进了平动点轨道相关研究的进展。文献[3]在FARQUHAR给出的地月系统共线平动点近似解析解的基础上，用数值方法得到了地月系统共线平动点附近的多族Halo轨道。文献[4]同样在FARQUHAR研究的基础上，论述了CRTBP三维Halo轨道及相应轨道簇的数值求解方法，并在原单步微分校正的基础上，针对Lissajous轨道不具备周期性的特点，采用多步打靶法实现了拟周期轨道的数值求解。上述研究成果大多是基于CRBTP模型得到的，但在实际的地月空间中，CRTBP模型不能完全反映真实的动力学环境，用该模型设计的轨道与实际存在较大差别，会明显增加轨控所需的燃料。因此，对CRTBP模型的改进又进行了大量研究。文献[1]在地月系统共线平动点轨道设计中考虑了太阳引力的作用，用月球轨道平均要素及引力展开成无穷级数后的有限项逼近。文献[5]在CRTBP基础上提出限制性四体模型，并以CRTBP的Halo轨道为初值，用数值法得到了四体问题的周期轨道。此后，Howell课题组在研究CRTBP问题时采用喷气推进实验室(JPL)的星历表(Ephemeris)数据，建立了高精度的动力学模型，并将其用于多个任务设计，但未给出更详尽具体的轨道设计细节[6-9]。目前，国内在该领域的研究和应用较少，仅少数高校开展过相关工作，研究在真实力环境中设计平动点轨道有一定的理论意义和较大的工程价值。

到目前为止，对传统CRTBP的理论研究已较成熟，而针对平动点附近更精确动力学模型的研究及轨道设计仍存在挑战。尤其是地月系统中，平动点附近动力学环境非常复杂，轨道稳定性较差，CRTBP的结果与实际轨道差别较大。如考虑的假设条件过多，设计的轨道精度不高，将严重影响航天器在轨飞行的时间和保持所需的燃料。本文针对上述问题，以地月系统共线平动点为背景，在不设置任何假设条件的条件下直接在惯性系中建立动力学模型，并采用轨道拼接和多步打靶法，调用星历表数据设计更符合真实的地月空间动力学环境的拟周期轨道。

1 坐标系统

建立高精度星历模型和数值仿真需使用坐标系4个：描述CRTBP的旋转坐标系、J2000地球赤道面惯性坐标系、地心瞬时旋转坐标系和平动点瞬时旋转坐标系[10]。如图1所示：CRTBP坐标系未单独绘出，若假设月球公转轨道为正圆形且转速恒定，则该坐标系与平动点瞬时旋转坐标系平行。具体定义如下。

a)CRTBP的旋转坐标系O-xyz：假设月球绕地球公转轨道为正圆，且轨道角速度恒定，以地球和月球公共质心为原点O，Ox轴从地心指向月心，Oy轴与月球绕地球公转的角速度方向重合，Oz轴与Ox、Oz轴构成右手垂直坐标系。

b)J2000地球赤道面惯性坐标系OI-xIyIzI(J2000 GECS)：以地心为原点OI，J2000历元时刻地球平赤道面为参考平面，OIxI轴从原点OI指向J2000历元时刻的春分点，OIzI轴与参考平面法线正向一致，OIyI轴与OIxI、OIzI轴构成右手垂直坐标系。

c)地心瞬时坐标系OE-xEyEzE(GRCS)：以地心为原点OE，OExE轴从地心指向月心，OEzE轴与月球绕地球公转的瞬时角速度方向重合，OEyE轴与OExE、OEzE轴构成右手垂直坐标系。

d)平动点(L2)瞬时旋转坐标系OL-xLyLzL(LCRCS)：以所选取的平动点，如L2点为原点OL，OLxL、OLyL、OLzL轴分别与OE-xEyEzE系的OExE、OEyE、OEzE轴平行，仅原点移动到至瞬时平动点的位置。

2 星历模型

目前在限制性三体问题的研究中，用星历表数据可选择的建模方式主要有在J2000惯性系中或在地心旋转系中建立动力学模型两种。因J2000系中的模型相对简单，故本文用前者进行建模。J2000系中航天器m、地球、太阳，以及月球间的位置矢量如图2所示。

`本文只考虑地球、月球、太阳引力和太阳光压力的影响。因太阳系中各天体均围绕太阳系质心(SSB)运动，故J2000坐标系中太阳系质心可视为惯性点，航天器相对地球(原点)的位置矢量可表示为

rp=rpssb-rEssb

(1)

式中：rpssb，rEssb分别为航天器和地心相对太阳系质心的位置矢量。本文所有天体位置信息均通过SPICE在MATLAB中的工具箱MICE从星历表bsp文件DE421中提取。根据牛顿定律，航天器在J2000坐标系中的星历模型方程为

(2)

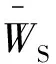
rpS=rp+rES

(3)

rpM=rp+rEM

(4)

若考虑其他天体的影响，则在式(2)中添加相应的引力项即可。

3 CRTBP周期轨道设计

在设计高精度拟周期轨道时需以CRTBP的轨道作为迭代初值，本文先给出CRTBP周期轨道的设计方法。旋转系中单位归一化后平动点附近的航天器动力学方程为

(5)

(6)

(7)

式中：x，y，z为航天器的位置坐标；μ为月球与地月系统总质量的比值；

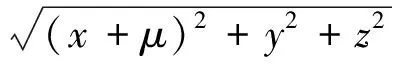
将该动力学方程写成状态空间的形式，有

(8)

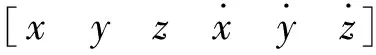
(9)

式中：Df(x(t))为f(x)在x(t)处的Jacobi矩阵。设Φ(t,t0)=∂x(t)/∂x(t0)为式(8)描述的系统从时刻t0至时刻t的状态转移阵，则x(t)=Φ(t,t0)x(t0)，即状态转移矩阵反映两个时刻状态变量间的线性映射关系。Φ(t,t0)对时间求导可得

A(t)Φ(t,t0)

(10)

根据Φ(t0,t0)=I，给定初始条件x(t0)，用数值积分即可求得任意时刻的状态转移矩阵。

目前常用的CRTBP周期轨道数值设计方法为微分校正方法，其原理就是前时刻初始状态到目标时刻进行数值积分得到末端时刻状态与理想状态的偏差，通过状态转移矩阵对初始状态进行修正，使末端状态的偏差不断减小直至满足约束条件。数值积分的初值可通过LP法等摄动法求得[2]。

设目标状态为xdes(tf)，对x(t0)进行数值积分至tf,得到时刻tf的状态x(tf)。x(tf)求变分可得

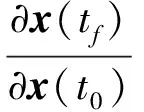
(11)

对式(8)、(10)进行1个周期的数值积分得∂x(tf)/∂x(t0)=Φ(tf,t0)，δx(tf)=xdes(tf)-x(tf)，再求解式(11)即可得初值的修正量δx(t0)和周期的修正量δtf。式(11)有未知量7个和方程6个，为减少计算量，可用轨道关于某一平面的对称性质，如Halo轨道在旋转坐标系内均关于平面XOZ对称，即轨道穿越XOZ平面时，有

y=0

(12)

(13)

(14)

4 星历模型的拟周期轨道

以上述CRTBP的周期轨道作为星历模型中拟周期轨道设计的迭代初值，通过调用星历表数据对轨道进行拼接可得所需的拟周期轨道。具体轨道设计步骤如下。

步骤1：选取星历模型需设计的拟周期轨道的起始历元时刻t0和终端历元时刻tf，历元时刻由世界时(UTC)给出并转化成星历时刻(ET)。起始时刻选定后，以该时刻地月间的距离为无量纲化的单位距离，在CRTBP模型中用微分校正方法生成相应的周期轨道。

步骤2：在历元时刻t0，tf间选取N个拼接点对应时刻ti，i=0，…，N-1。本文用时间等间距方法选取，将离散时刻ti转换至CRTBP模型中，求得对应的周期轨道上的状态，再根据这些离散状态对应的历元时刻和相应的天体位置信息将其转换至平动点瞬时旋转坐标系中，构成星历模型中的轨道节点状态初值。

步骤3：将前一步得到的平动点瞬时旋转坐标系中的节点状态作为迭代初值，用固定时间多步打靶法进行位置和速度校正，得到N-1段轨道弧段。当这些弧段在拼接点处的位置误差小于1×10-5km、速度误差小于1×10-8km/s时，可认为实现了位置连续和速度连续。

5 CRTBP系至J2000系的转换

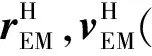
(15)

(16)

(17)

历元时刻t时地月旋转坐标系相对J2000系的角速度为

(18)

(19)

(20)

式中：TEM为月球绕地球的公转周期。根据式(19)、(20)可得从地月旋转系至J2000系的转换矩阵为

(21)

6 多步打靶法

在上述拟周期轨道设计中用多步打靶法替代单步微分校正进行迭代，这是因为与CRTBP模型不同，星历模型中平动点附近存在的轨道为拟周期轨道，不具备x(t+T)=x(t)的性质，故单步微分修正的方法已不适用，需用多步打靶法对轨道上的各节点进行校正以获得所求的轨道。

设轨道的使用寿命为T=tf-t0，将T等分为N个时间段，各时间段的节点分别为ti，i=0，1，2，…，N，其中tN=tf，时间节点处的状态为x(ti)。设Δt=ti+1-ti，以x(ti)为初值积分Δt时间后的状态为φ(x(ti))。当所有x(ti)均位于同一轨道上时，有

φ(x(ti))=x(ti+1)

(22)

由式(22)可得

φ(x(ti)+δx(ti))≈φ(x(ti))+Φ(ti+1,ti)δx(ti)=

x(ti+1)+δx(ti+1)

(23)

式(23)在N个时间段上均满足。联立N个方程组可得

(24)

式中：I为单位阵。令DF为-F在ΔX处的Jacobi矩阵，因矩阵DF行数小于列数，故该方程组有无数组解，其伪逆解为

δX=-(DF)T(DF·(DF)T)-1F

(25)

当N较大时，直接求解式(25)计算量会非常大，本文用文献[11]的方法简化求解过程。

设M=DF·(DF)T，引入变量Z=[Z1…ZN-1]T=M-1F，则式(25)变为

MZ=F

(26)

δX=-(DF)TZ

(27)

对M进行Cholesky分解，可得

(28)

式中：

D1=I+Φ(t1,t0)(Φ(t1,t0))T

Li=-Φ(ti,ti-1)(Di-1)-1

Di=I+Φ(ti,ti-1)(Φ(ti,ti-1))T-LiDi-1(Li)T

引入中间变量Y=[Y1…YN]T，则式(26)的解Z为

Y1=x(t1)-φ(x(t0))

Yk=x(tk)-φ(x(tk-1))-Lkδx(tk-1),

k=2,3,…,N-1

ZN-1=(DN-1)-1δx(tN-1)

Zk=(Dk)-1δx(tk)-(Lk+1)TZk+1,

k=2,3,…,N-1

再由式(27)即可求得各节点处的状态修正量δx(ti)。

7 数值仿真

用本文的共线平动点附近拟周期轨道的构造和分析方法，研究星历模型中地月系共线平动点附近的拟周期轨道。相关参数见表1。

用本文方法在地月系统L2点附近拼接的某条拟周期Halo轨道如图4～6所示。轨道运行时间为2014年7月1日0时至2015年7月1日0时，即1年的时间，所用拼接点数为200，形成弧段199个。

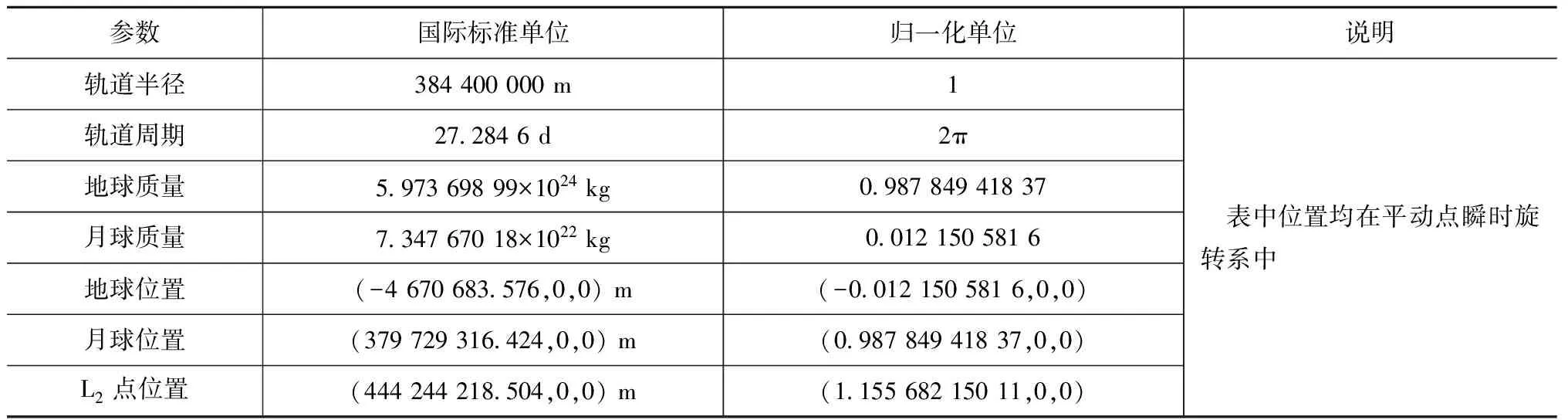
表1 地月系平动点基本参数

其中作为迭代初始轨道的Halo轨道的Z向幅值约10 000 km。为更清晰地给出拟周期轨道的形状、瞬时平动点的位置及航天器运行在该轨道上时与地球和月球的位置关系，并与CRTBP的轨道进行对比，分别在平动点瞬时旋转系、地心瞬时旋转系和J2000系中给出了设计的轨道。由图4～6可知：在地心瞬时坐标系中，由于月球偏心率等因素的影响，地月间的距离随时间变化，导致瞬时平动点沿X轴也呈现周期性变化，周期轨道的形状与CRTBP中的轨道差别较大，随平动点沿X轴作周期性摆动，但在平动点瞬时旋转系中，周期轨道的形状与CRTBP的轨道较为相近。

8 结束语

本文针对地月系统共线平动点附近动力学环境复杂，轨道稳定性差，对设计精度要求高的特点，考虑月球真实轨道以及地球、月球和太阳的影响，在惯性系中建立了地月系统平动点附近航天器的高精度星历模型。针对在CRTBP设计的轨道精度不高的问题，以CRTBP的周期和拟周期轨道为初值，用轨道拼接方法和多步打靶法设计了星历模型中的拟周期轨道，并用数值仿真对算法进行了验证。仿真结果表明：本文设计的算法可有效获得所需的轨道。

本文所研究内容可为平动点附近的航天器提供满足真实动力学环境的轨道，有效节省轨道保持所需的燃料。

[1] FARQUHAR R W, KAMEL A A. Quasi-periodic orbits about the translunarlibration point[J]. Celestial Mechanics, 1973, 7(4): 458-473.

[2] RICHARDSON D L. Analytic construction of periodic orbits about the collinear points[J]. Celestial mechanics, 1980, 22(3): 241-253.

[3] BREAKWELL J V, BROWN J V. The Halo family of 3-dimensional periodic orbits in the Earth-moon restricted 3-body problem[J]. Celestial Mechanics, 1979, 20(4): 389-404.

[4] HOWELL K C. Three-dimensional periodic ‘Halo’ orbits[J]. Celestial Mechanics, 1984, 32(1): 53-71.

[5] HOWELL K C, Spencer D B. Periodic orbits in the restricted four-body problem[J]. Acta Astronautica, 1986, 13(8): 473-479.

[6] PAVLAK T, HOWELL K. Strategy for optimal, long-term stationkeeping of libration point orbits in the Earth-moon system[C]// AIAA/AAS Astrodynamics Specialist Conference. Minneapolis: AIAA/AAS, 2012: 13-16.

[7] OZIMEK M T. Low-thrust trajectory design and optimization of lunar south pole coverage missions[D]. Purdue: Purdue University, 2010.

[8] WAWRZYNIAK G G. The dynamics and control of solar-sail spacecraft in displaced lunar orbits[D]. Purdue: Purdue University, 2011.

[9] PAVLAK T A. Trajectory design and orbit maintenance strategies in multi-body dynamical regimes[D]. Purdue: Purdue University, 2013.

[10] 钱霙婧. 地月空间拟周期轨道上航天器自主导航与轨道保持研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.

Quasi-PeriodicOrbitDesignaroundEarth-MoonLibrationPointsUsingEphemerisModel

LIU Gang1, 2， HUANG Jing1, 2， GUO Si-yan1, 2

(1. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China;2. Shanghai Institute of Spacecraft Control Technology, Shanghai 201109, China)

In order to improve the insufficient of lacking perturbation analysis during the orbit design process by using the circular restricted three-body model and increase the accuracy of the orbit design, the method of quasi-periodic orbit design around the Earth-moon libration points using ephemeris model was studied in this paper. Without any assumptions, the high-accuracy ephemeris model for spacecraft around the Earth-moon libration points was established in the J2000 inertial coordinate system with the consideration of real moon orbit and effect of the Earth, moon and sun. The periodic orbit in circular restricted three-body problem (CRTBP) was treated as the iterative initial value. The quasi-periodic orbit was obtained by orbit conjoint using ephemeris parameters. The single differentiation modification was taken placed by multiple-shooting method for iteration. The points in the orbit were corrected to obtain the quasi-periodic orbit. The design steps were given. The simulation results showed that the quasi-periodic orbit around libration points in the Earth-moon system would be obtained, which could provide the orbit that satisfied for real dynamic environment and save fuel for orbit keeping. The method has some application valuable in enginerring.

Earth-moon system; libration point; restricted three-body problem; solar radiation; gravity perturbation; quasi-periodic orbit; multiple shooting method; ephemeris

1006-1630(2017)05-0016-07

2016-11-19；

2016-12-15

刘 刚(1985—)，男，博士，主要研究方向为航天器轨道与姿态控制、航天器轨道设计、非线性控制、最优控制等。

V412.41

A

10.19328/j.cnki.1006-1630.2017.05.003