案例解析 数学学困生的自主学习模式
2017-11-03广东省广州市南沙麒麟中学511455武志容
广东省广州市南沙麒麟中学(511455) 武志容
案例解析 数学学困生的自主学习模式
广东省广州市南沙麒麟中学(511455) 武志容
一、模式建构
曹一鸣老师根据其对教学效果的影响提炼出了16个关键教学行为,如图1:
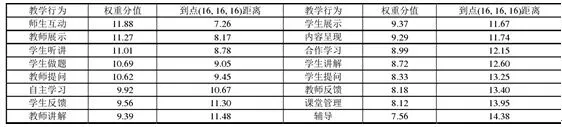
图1
结合上述研究结果和对各种教学模式的借鉴,我们提炼出以下的自主学习模式,以学生的自主学习、小组合作为基本环节,力争提高学困生的学习兴趣.
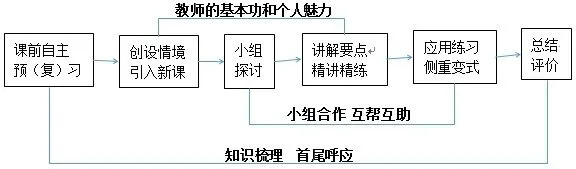
图2
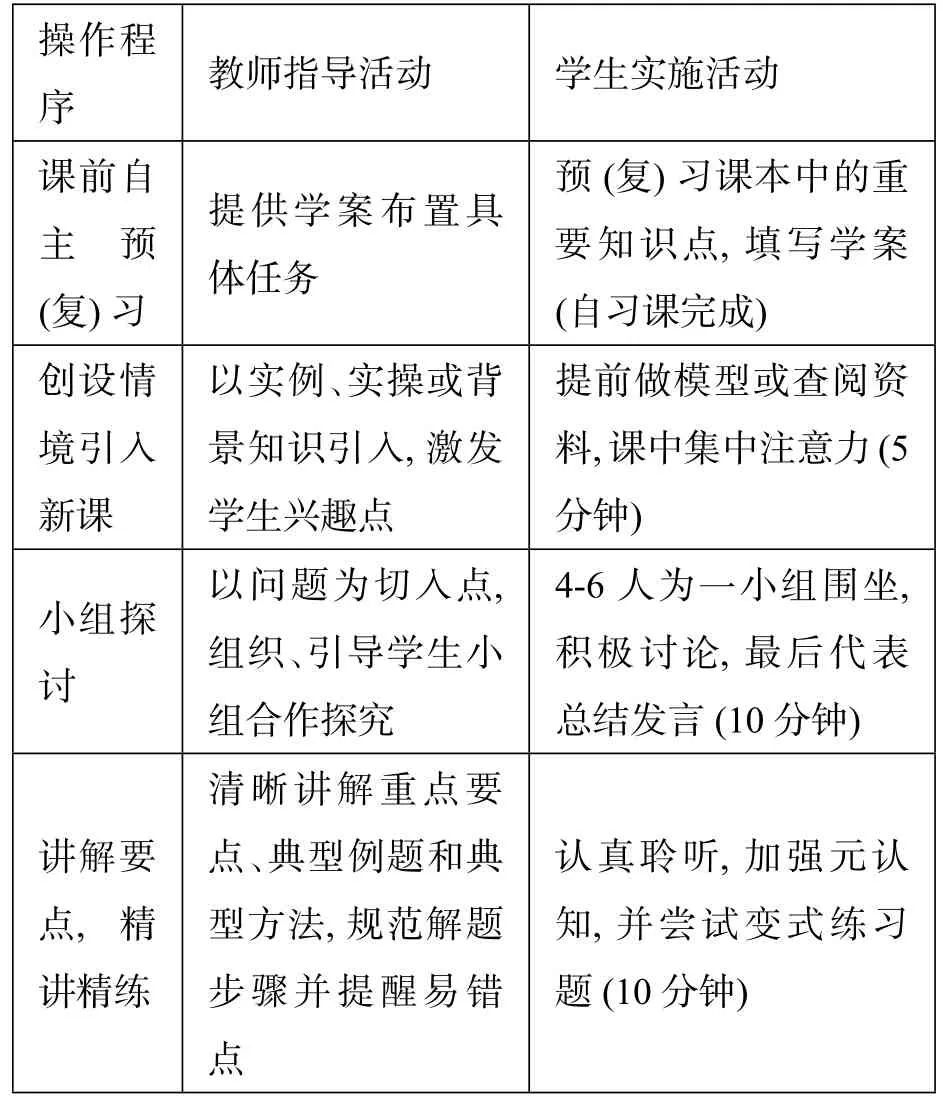
师生互动情况表

应用练习,侧重变式提供变式训练题3-4道,巡视学生解题情况,并个别辅导先独立完成,后组内交流解法、结果(15分钟)总结评价与学生一起回顾、总结知识要点反思、总结相关知识点(1-2分钟)
二、案例
高中数学必修3《3.2古典概型》(第一课时)
课前自主预习课本第125-130页
模拟试验1:掷一枚质地均匀的硬币试验,请写出可能出现的结果:___________
模拟试验2:抛掷一只均匀的骰子一次,请写出点数朝上的试验结果:___________
基本事件的两个特点:(1)___________;(2)___________.
观察对比,以上两个模拟试验和课本例1有什么共同特点?(1)___________;(2)___________.
一般地,对于古典概型,如果试验的基本事件总数为n,随机事件A所包含的基本事件数为m,则事件A的概率,记作P(A)=___
创设情境引入新课
师:概率来源于赌博,在17世纪的欧洲宫廷中盛行着“赌博游戏”,贵族们热衷于估计游戏中各种可能结果发生的概率,这直接影响到他们在游戏中的收益.当时大名鼎鼎的数学家帕斯卡、费马等人也常常被贵族们咨询关于赌博的问题.以下就是当时一个非常经典的问题:同时投掷两枚骰子,游戏参与者事先可以选择点数之和小于等于6或者大于6,问应选择何者可使获胜的机会更大?今天我们穿越时空,来到文艺复兴时期的欧洲宫廷,各位同学可否帮助贵族们解决上述问题?
A生:应该选择大于6的,因为大于6的有7,8,9,10,11,12共6个机会,而小于等于6的只有2,3,4,5,6共5个机会
B生:不对哦,一个骰子5点一个骰子6点,和都是11点,但却是两种不同的情形
师:下面大家动手列一列,看看到底有多少种可能的结果,注意要全部考虑到不能重复也不能遗漏.以小组为单位讨论一下.
小组探讨讨论结果主要有下面2种:(小组代表发言总结)
1)(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,2),(2,3),...,(6,6)共21种;
2)(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),...,(6,6)共.种;
师:现在有2种结果,都是说明后者获胜的机会大,但哪一种的列举情况更合理呢?
D生:应该是第二种更合理,因为(1,2)与(2,1)是两种不同的情形.
师:嗯,这个同学考虑比较完善了,像这种问题我们首先要考虑总共有多少种情形,每一种情形还能不能再分解,如点数之和为5的可以分解成(1,4)和(2,3);再考虑(1,4)与(4,1)是一种情形还是两种,每一种独立的情形就是一个基本事件.
小结基本事件的2个特性:互斥性、完备性
例1从字母a,b,c,d中任意取出两个不同字母的试验中,请写出试验的基本事件?
解所求的基本事件有:(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)共6个.
E生:这里的(a,b)为什么只有一个,不是应该还有一个(b,a)的吗?所有基本事件应该是有12个.
F生:这里说“任取两个”,没说要先取什么后取什么,所以这里的(a,b)与(b,a)是同一种情况,应该只能算一种.
师:F同学说到问题的本质了,也就是在基本事件中如果有次序的要求就应该算2种,如果没有次序的要求那么这2种就都是一样的情形,那全部都算1种就可以了.
小结上面两例出现的基本事件的共同特点:有限性、等可能性古典概型事件的概率为:

讲解要点、精讲精练
类型一古典概型和基本事件的理解
例2下列试验是古典概型的是( )
A. 在适宜的条件下,种下一粒种子,观察它是否发芽;
B. 口袋里有2个白球和2个黑球,这4个球除颜色外完全相同,从中任取一球;
C.向一个圆面内随机地投一个点;
D.射击运动员向一靶子进行射击,考察他的射击结果.
答案B
类型二古典概型概率公式
例3 单选题是标准化考试中常用的题型,一般是从A,B,C,D四个选项中选择一个正确答案.如果考生掌握了考试的内容,他可以选择唯一正确的答案.假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?
解设事件A为“选中的答案正确”,试验的基本事件总数n=___;事件A所包含的基本事件数m=___代入
变式1 扔一枚质地均匀的骰子,求“出现偶数点”的概率.
例4同时掷蓝、白两个不同的骰子
(1)请列出所有不同的结果;
(2)其中向上的点数之和是5的有多少种?
(3)向上的点数之和是5的概率是多少?
解(1)共36种结果,(可列举也可用表格表示);
(2)点数之和为5的有(1,4),(4,1),(2,3),(3,2)共4种;
(3)设“点数之和是5”为事件A,则
变式2 从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是( ).

应用练习、侧重变式
1、小明、小刚、小亮三人正在做游戏,现在要从他们三人中选出一人去帮助王奶奶干活,则小明被选中的概率为____,小明没被选中的概率为___.
2、任意选取一个两位数,它恰好是10的倍数的概率是( )
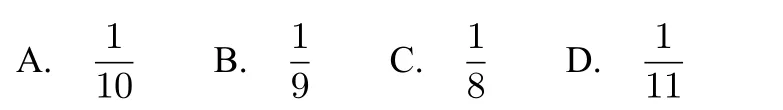
3、一个袋中装有3个红球和2个绿球,从袋中每次取1球,取出后放回,连续取两次,求:
①取出的两球中恰好有一个是红球的概率;
②取出的两球中至少有一个是红球的概率;
③若将上面②中更改为“取出后不放回”,结果又会如何呢?
总结评价这节课我们知道了基本事件的两个特点:_______,以及古典概型的两个特征:_______,其概率公式:P(A)=________,在找基本事件时要注意不能重复也不能遗漏,要注意实验本身蕴含的基本事件是否有顺序的不同.
三、模式分析
学困生通常对数学不感兴趣或望而生畏,我们通过课前预(复)习给他们一个缓冲,让他们有一个适一个适应的过程;再通过实例、实操等多种形式引入新课,增强他们的学习兴趣;小组合作充分发挥以优带差、互帮互助的作用,使学困生也能参与其中并有所收获;教师的讲解要点和学生的应用练习,是对新学知识的巩固和加深,考虑到学困生的基础水平和理解能力,教师的讲解以“双基”为主,学生的练习也紧扣知识要点;最后师生共同总结帮助进一步回顾知识要点以加深印象.整个教学模式是从具体课堂中提炼而来,既秉承传统又有创新探索.每个环节承上启下、过渡自然,有大致的时间分配,少讲多练,师生互动频繁,课堂气氛活跃,小组讨论展示环节给学生极大的自主权,教师上课轻松,学生也可以自由发挥.
有的老师可能会认为“教无定式”,课堂教学瞬息万变,需要根据不同的情形随机应变.好的教学模式可以让教师在上课时做到有章可循、心中有数,自然学习效率就高.我们说教学是一门艺术,建立模式是为了最终摆脱模式,从无序状态走向有序,这是第一次提升;从有序走向自由,达到“无模式化”,这是第二次升华.我们每一个老师只有做到心中有模式,然后灵活运用多种模式,形成自己的教学风格,最后才能超越模式,超越自己.
