构建解题思路 反思课堂教学—一类二元变量证明题的解题策略

江苏省泰州市姜堰中学(225300) 王立振

构建解题思路 反思课堂教学—一类二元变量证明题的解题策略

江苏省泰州市姜堰中学(225300) 王立振

1、前言

当下,高中生学习数学最大的困难是不知如何解题、怎样解题,数学概念基本能听懂,习题课的效果也不错,但是学生一旦自己动手解题时,往往就束手无策,不知从何入手,导致功夫没少下,效果并不佳的情况,从而丧失学习数学的兴趣和动力.

著名数学家波利亚解题理论告诉我们——解题要做“七分构思”(读题、审题、发散、联想、归纳),“三分表达”(书写、运算、订正、反思与回顾).高三复习教学无外乎就是教会学生如何解题、怎样解题及课后的自我整理消化.不只是简简单单地把一道题目讲清楚讲明白,而是教会学生如何构建条件与目标之间的关系,并引导学生在课后进行自我消化与总结,这才是高三复习教学的重中之重.

2、难在何处

二元变量的证明问题在每年的全国各地的大型考试、模拟试卷甚至高考试卷都出现过.学生心有余悸的二元变量证明题到底“难”在何处?一般来说,一是难在证明形式的复杂(2016届陕西师大附中高三下第十次模拟文科试题);二是难在无从下手(2016届安徽六安一中高三下模拟四理科试题);三是难在知识与方法的综合(2015-2016学年江苏如皋中学高二下月考试).

3、赏析解题策略

例1 已知函数f(x)=(a+1)lnx+ax2+1,证明:当a＜−1时,对任意的x1,x2∈(0,+∞),恒有|f(x1)−f(x2)|+4|x1−x2|≥0.

策略1 从目标结构出发,转化为新函数单调性的证明.如果我们单纯从结论出发,求|f(x1)−f(x2)|+4|x1−x2|的最小值恒大于等于零.首先讨论x1,x2的大小关系,去掉绝对值,再求含有两个变量的表达式最小值,且表达式较为复杂,可想而知这样的解题是繁琐的.那么有无简化的可能?该如何简化解题?事实上,我们观察不等式的结构可以发现,含有x1的多项式中只有x1,x2,也是一样的.可将含有x1,x2的多项式左右分离,分别置于不等号的左右两边,再利用新函数的单调性就可证明.

解析因为a＜−1,所以对于x∈(0,+∞),f′(x)＜0,有f(x)单减.不妨设0＜x1＜x2,

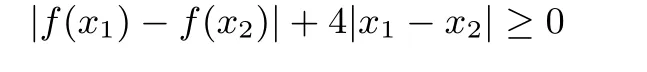
转化为

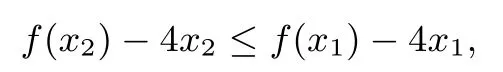
令g(x)=f(x)−4x,当0＜x1＜x2时,有g(x2)≥g(x1),则函数g(x)在(0,+∞)上单减.即证明g(x)的导函数g′(x)在(0,+∞)恒有

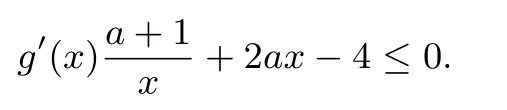
因为a＜−1,x＞0,所以有则有∀x∈(0,+∞),g′(x)≤0,故结论成立.

点评将不等式进行变形后,使得含有x1,x2式子分别置于不等式的左边和右边,形如:g(x1)＜g(x1).从而将两个变量的不等式证明问题转化为新函数单调性的证明问题,转化为学生易知、易求的问题.

例2 已知函数f(x)=xlnx,证明,对于任意的x1,x2∈(0,+∞),都有f(x1)+f(x2)+x1+x2＞f(x1+x2).

策略2 从变量形式出发,转化为一元变量的恒成立问题.从目标中变量所给的形式出发,若二元变量可通过适当变形,使得x1,x2都以的整体形式出现,那么我们可以通过整体换元,达到减元的目的,起到减少变量的效果.

解析将不等式进行化归转化:

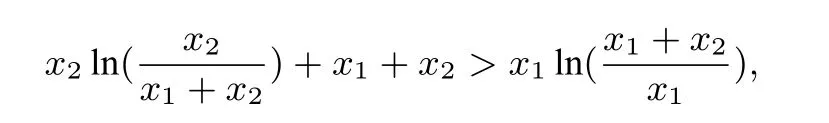
不等式两边同时除以x2,可得

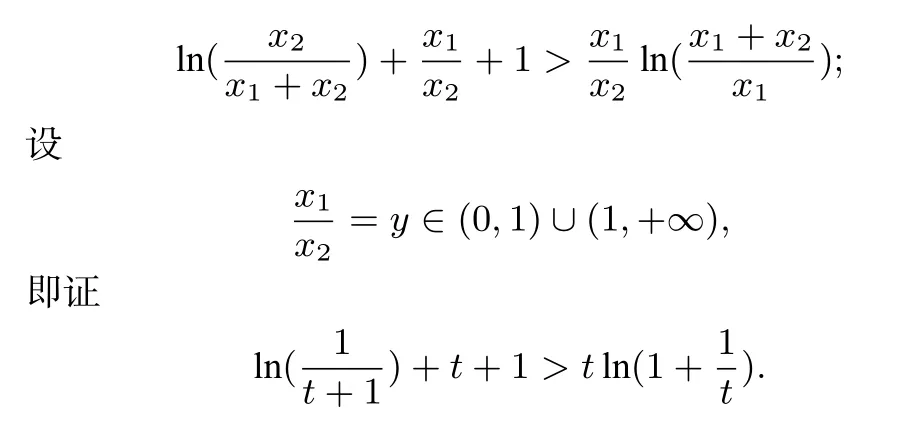
令函数

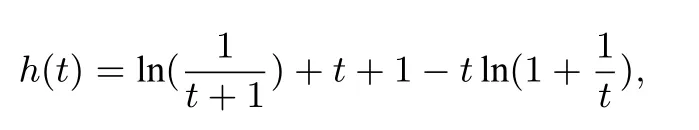
其导函数

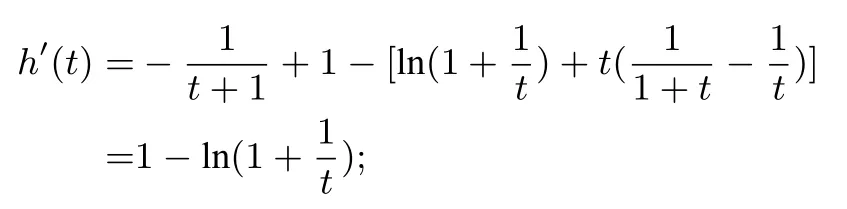
令h′(t)=0,易知存在t0,有

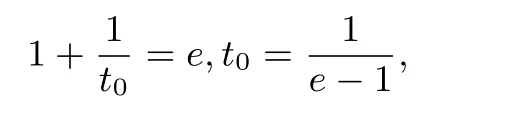
且h(t)在(0,t0)单调减,(t0,+∞)单调增.则有

点评改变思考问题的角度.通过对不等式的变形和转化,不等式中两个变量都是的形式出现,将整体换元,从而将二元变量的不等式证明问题转化为一元变量的恒成立问题,使难解的问题简单化,熟悉化.

策略3 从变量个数出发,变量转参数构造新函数.

有多元变量不等式的证明问题,即有两个变量且变量间没有内在的联系.如果我们从变量个数出发,把x2看成变量x,x1看成参数,这样不仅减少变量的个数,而且转化为学生熟悉的、易入手的一元变量的不等式问题.

解析1 将参数x2变为未知数x,记

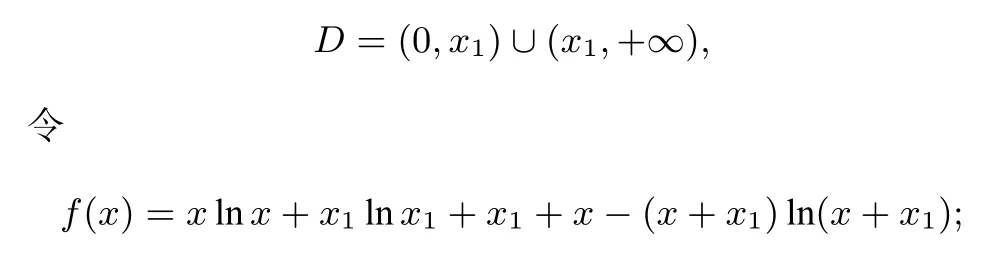
其导函数

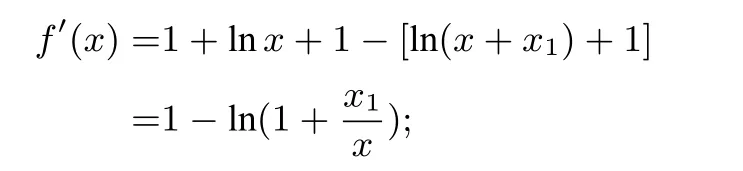
令f′(x0)=0,存在

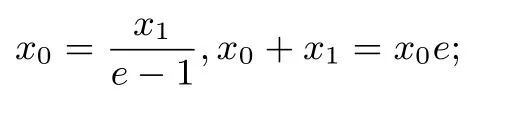
使得f(x)在(0,x0)单调减,在(x0,+∞)单调减.所以

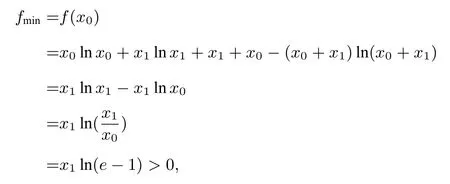
有∀x2∈D,f(x2)＞0,易知

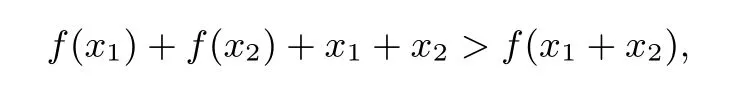
即结论成立.

点评将不等式中x2转化为变量x,x1看作参数,使得上述不等式的证明问题转化含有一个变量不等式恒大于零的问题,再利用导数求出最小值,即可得证.而解题的关键在于转换参数与变量的角色.(构造的新函数不唯一,本题还可有如下构造)

解析2 当x1=x2时,结论显然成立,否则不妨设0＜x1＜x2,设

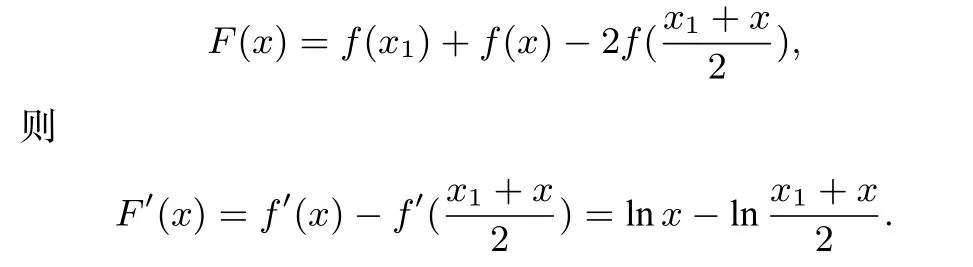
当0＜x＜x1时,F′(x)＜0,F(x)在(0,x1)上为减函数,当x＞x1时,F′(x)＞0,F(x)在(x1,+∞)上为增函数,则有

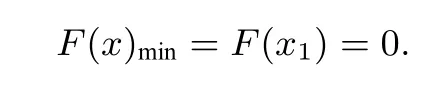
当x2＞x1时,有

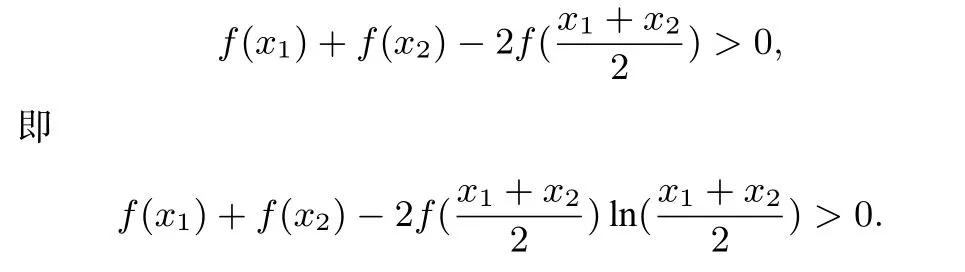
化简可得:

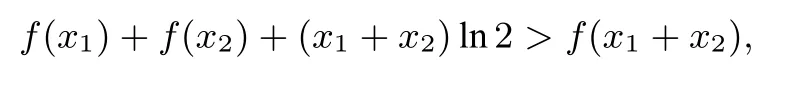
即

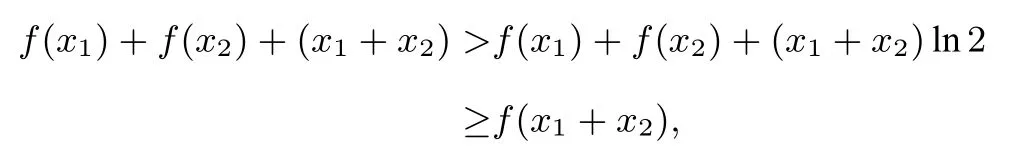
故结论成立.

解析3 对于m＞0,令F(x)=f(x)+f(m−x),0＜x＜m,则当即F′(x)＜0时,F(x)在区间上单调递减,当即F′(x)＞0时,F(x)在区间上单调递增;因而对所有的0＜x＜m,都有即

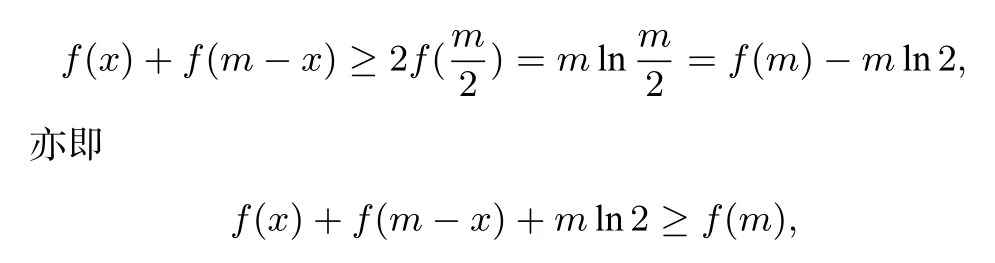
取x=x1,m−x=x2,得

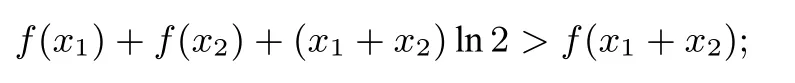
故有

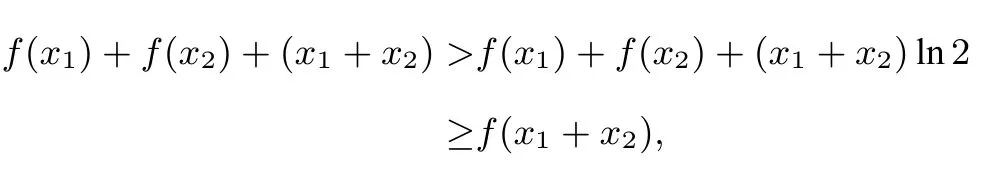
结论成立.

一种漂亮解法的得出,需要我们对以往思路构思及经验的不断总结,更需要我们对问题有更深层的剖析.

4、教学启示

任何数学问题都存在于某类问题的共性之中,利用数学中这种共性结果处理数学学习的困难.通过这类题目解法及其分析可知,这类题目思维角度较小,解题方法固化,所用知识也是常规的,但学生做题还是问题不断,漏洞百出.在平时教学中我们需要多关注的是什么呢?

4.1 解题应以“构思”为纲

在现代任职心理学中,人的任职活动并非是对外部世界的简单被动的反映,而是一个主体在其中发挥主观积极能动性的过程.因此,高三复习教学活动不应看成教师教授知识,学生被动接受,而是启发学生在已有的知识和经验的基础上,主动构建解题思路的过程.教师可根据每节课的教学内容不同,寻找一个引发问题的“生长点”,启发学生,积极构思,培养学生勤于思考,善于构思的习惯,使学生具有悟性.

4.2 课堂教学应以“反思”为魂

反思是什么?反思就是在解决完一道数学题后还需认真进行如下的探索:该题的命题意图是什么?考查了哪些基本知识和基本方法?解题过程是否合理、是否完善?有无其他解法?该题的解法是否具有一般性(即举一反三、一题多变、一题多解)?以上的思考就是教学反思.教学反思有助于培养学生思维的广阔性,提高思维的灵活性,最终帮助学生提高发现问题、分析问题、解决问题的能力,从而真正实现罗增儒老师倡导的“通过有限典型例题的学习领悟解无数道题的数学机智”.