学生质疑从哪来

广东省中山市沙溪初级中学(528400) 林天雄

学生质疑从哪来

广东省中山市沙溪初级中学(528400) 林天雄

本学期的一天中午,数学中段考刚结束,我正想离开办公室回家.这时一(5)的罗秋平(一个数学成绩中等的女孩子)走进来问我中段考里的一道题:若一个多边形的每一个内角都是108°,则这个多边形是___边形.我不假思索地回答是正五边形,秋平说:“五边形对吗?” .我说不对.倾刻间她又说:“老师,你不是说过正多边形要求每个内角都相等,且每条边都相等吗?”我说这是定义,没错,若你能举出一个反例,我不但给你对,还给你多加20分.她还有点不相信我的鼓励问了一句:“真的吗?这可是你说的?”回家的路上,我只是想了一下,没能找到反例,就做罢了,没继续探究.

星期一数学课上,罗秋平很高兴告诉我:“老师,我找到反例了.” ,我很高兴让她当众说说.她陈述作正五边形的任一边的一条平行线,然后延长与这条边相邻的两边,形成的新五边形每个内角都相等,但不是正五边形.如图1.

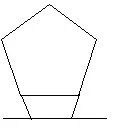
图1

在事实面前,我肯定了秋平的正确,还当着全班同学面大大表扬了她一番,承认了我的错误,秋平好学钻研问题,精神可佳自不必说,但敢于质疑老师,我想这和我平时的教学不无相关.以下结合本人的数学教学经验,就如何培养学生质疑的能力,谈谈几点粗浅看法,供读者参考.

一、创设以学生为本的课堂气氛,学生才敢质疑

以学生为本就要尊重学生作为人的本性.“学起于思,思源于疑.”好奇是儿童的天性,学生对身边的事物充满好奇,总爱提很多问题,并主动地进行探索.爱因斯坦曾说过:“提出一个问题比解决一个问题更重要.”这说明:人们要想在学业上有所成就,科学上有所发明创造,就必须从质疑问题开始.因此,在数学课上让学生质疑,倡导学生之间的自由探索,有利于学生形成质疑的能力,为学生的创新意识提供了土壤.

平常我喜欢说老师不是圣贤,不是权威,老师说得不是的地方,你们要大胆提出来,我们共同探究解决.对学生的质疑,如果我一时回答不上来,我不会不懂装懂,甚至堵塞言路,诸如“连这样的题都不会,下去仔细想想.”“这样的题不需要掌握.”这样就会挫伤学生的求知欲,挫伤学生参与的主动性,我回答不上一般如实地加以说明,请学生帮忙解答,或暂且放下,课后再去寻求解答.学生质疑是学生主动参与的重要表现,善于引导和鼓励学生质疑使学生积极参与,40分钟的堂上效率会大大提高,课堂教学一定会收到好的效果.

二、创设疑惑情景,使学生乐于质疑

兴趣是儿童入门的先导.爱因斯坦说过:“最好的老师莫过于热爱.”儿童有了热爱就有了学习的动力,就会在活动中主动地获取知识.因此,老师要善于根据学生的年龄和心理特点,创设新奇别致的问题情境,使学生置身于“心欲求而不得,口欲言而不能”的情境中,从而激发学生的求知欲,提高学生的质疑兴趣,以趣生疑,使学生的思维更加主动、积极.学生质疑能力的发展及培养,不仅有赖于知识和能力的基础,而且还要依赖于问题情境的设置.例如:在教学《无理数有多大》引入新课时,我说,是无理数,即无限不循环小数,到底小数点后有多少位谁也说不清,但我们能用几何作图的方法或在数轴上准确确定它的大小.请根据图2独自或和同学探究这一问题(之前未学过勾股定理).假设△ABC直角边AB=BC=1,你能求出AC的长吗?

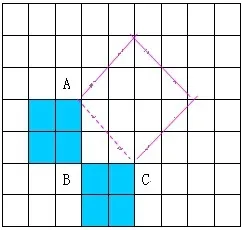
图2

为了明确解决问题的目标,可引导学生从如下几个方面质疑:①一个小正方形的面积是多少?②大的正方形的面积是多少?③AC和大正方形的边长有什么关系?④大正方形和小正方形的面积有什么关系?⑤你能否用方程求出AC的长度?另外当学生知道边长为1的正方形的对角线长就是时,要学生质疑数轴能否表示无理数,即在数轴上能否准确找到一点和相对应?这样大大拓展了学生的思维空间,培养了质疑能力,使学生产生浓厚的学习兴趣.

三、教给学生质疑的方法

从心理学角度来说,好问和好奇是儿童的天性,是儿童求知欲的表现.教师要善于利用儿童这份天性,教给质疑方法,让学生学会把学习过程中有价值的疑难问题提出来.

1.掌握结构,质明确疑方向

在数学课堂教学中,采用质疑这一教学手段,可以以一个单位的教学内容为独立单位,建立相应的质疑方法.教师在教学时做好示范提问,让学生了解可以从哪些方面着手提问,为今后学生正确迁移独立质疑做好铺垫.例如:七年级第二学期教材中“代入法解二元一次方程组”的教学,这一个部分内容分成三个知识点:直接用一个方程代入另一个方程进行消元;方程组中其中一方程有一个未知数的系数为1或−1,进行简单的移项变形就可代入消元;方程组中未知数的系数都不为1或−1.教材中安排三个相应的例题:

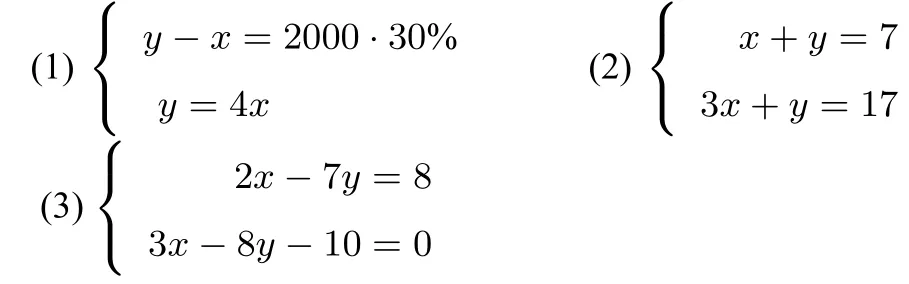
通过每个例题计算过程,强调代入可消元,把二元转变为一元,使学生了解知识结构的网络.因此教师在例(1)的教学时,应要强调解二元一次方程组的目的是消元,把二元一次方程组转化为我们熟悉的一元一次方程.教给学生可以从:(1)例题的特征;(2)代入的前提条件;(3)等量代入的整体思想;(4)代入符号处理;(5)未知数是怎样被消掉的?(6)计算出一元的值后,如何求另一元的值?等方面进行提问.这样,学生既掌握了知识结构和学习过程结构,又明确了质疑的方向,为例(2)、例(3)的迁移做好铺垫.

2.正确迁移,大胆尝试质疑

迁移可以是多方位的,一个单元内每个例题的学习可以迁移;单元与单元之间的学习也可以迁移,只要具备了可以类比的结构都可以进行迁移,例如:在学习“解一元一次方程”的基础上,学习“解一元一次不等式”时,就可以照“解一元一次方程”的质疑方法,进行类比,从而得到“解一元一次不等式”质疑可以从以下几个方面着手提问:(1)例题的特征是什么?(2)运算法则是什么?(3)一般的运算步骤是什么?(4)左右两边同乘(除以)一个负数怎么办?(5)与解一元一次方程的不同点在哪里?…

3.把握重点,善于质疑

当学生有了一定的质疑能力,教师要抓住契机,及时引导学生思考哪些问题该问,哪些问题不该问,例如:七年级教材中“近似数和有效数字”中的0.0158和0.01580,学生从“计算结果大小”方向提问,这一问题显然无意义,但是“它们表示结果的意义相同吗?”同样从“计算结果”提问,这一问题显然要比前一个问题质量高多了,这个问题含盖了前一个问题,同时又暗示了精确度不同,有效数字的个数也不同,后一近似数比前一近似数的精确度高.

总而言之,培养学生质疑能力的方法很多,关键在于教师要更新教学观念,优化教学方法,提供多种的观察、操作、思维及语言表达的时机,鼓励和引导学生主动参与学习的全过程,使学生对所学知识感到有问题可想,有问题可提,有问题可议,由被动质疑逐步转向主动质疑,帮助学生认识自我,建立信心,从而调动其学习主动性和积极性,使学生在创新能力和思维能力等多方面得到发展.