双壳油船破舱原油泄漏缩尺模型相似准则
2017-11-03卢金树吴豪霄杨振波
卢金树, 吴豪霄, 杨振波
(浙江海洋大学 海运与港航建筑工程学院, 浙江 舟山 316022)
2017-04-15
国家自然科学基金委员会面上项目(51079129);浙江省自然基金(LY18E090008)
卢金树(1974—),男,浙江象山人,教授,从事船舶安全与污染控制研究。E-mail:ljs_ljs@zjou.edu.cn
1000-4653(2017)03-0103-06
双壳油船破舱原油泄漏缩尺模型相似准则
卢金树, 吴豪霄, 杨振波
(浙江海洋大学 海运与港航建筑工程学院, 浙江 舟山 316022)
为使双壳油船原油泄漏缩尺模型试验能真实地反映事故原型,需确定各相似准则的重要程度。针对油舱原油泄漏过程,基于相似理论,采用量纲分析的方法推导较完整的相似准则数群,根据不同相似准则的组合建立3种缩尺模型。进行原型和不同相似准则缩尺模型的数值试验,并根据相似关系将缩尺模型试验的泄漏持续时间、泄漏总量等宏观泄漏特征参数反推回原型,与原型数值试验结果相对比。采用黏性流体动力学理论分析各种作用力对泄漏过程的影响。结果表明:弗汝德相似准则和雷诺相似准则是原油泄漏缩尺模型试验必须依据的准则,韦伯相似准则可不予考虑。在试验油品和原油密度相同的情况下,缩尺模型试验结果与原型最为接近。针对不同泄漏阶段,应采用不同的缩尺模型进行试验。
船舶工程;缩尺模型;相似准则;原油泄漏;双壳油船;黏性流体动力学
在原油泄漏研究中,原油泄漏规律的精准预测是研究者关注的两大工程问题之一。[1-2]针对该问题,通常采用理论分析、数值模拟和模型试验等方法进行研究。由于油品泄漏涉及到的流动行为复杂多样,采用理论分析方法时需对泄漏预测模型进行大量简化,导致模型精度不高。大尺度模型试验能得到较为真实的原油泄漏规律,但大尺度模型舱的制作成本较高,且原油泄漏会造成严重的环境污染。[3]因此,通常采用小尺度缩尺模型试验的方法研究原油泄漏规律。[4-7]缩尺模型试验的精度主要受以下3个因素影响:
1) 确定原油泄漏过程的主导力,选取合理的相似准则。
2) 选取表征泄漏特征的特征长度。
3) 选取适当大小的缩尺比。
关键作用力的相似准则缺失、表征泄漏特征的特征长度选择错误及缩尺比过小都有可能引发缩尺效应。根据建立缩尺模型所依据的相似准则分类,采用的缩尺模型主要有弗汝德相似准则模型(以下简称Fr模型)和弗汝德-雷诺相似准则模型(以下简称Fr-Re模型)2种。
Fr模型是早期的原油泄漏模型试验中采用的缩尺模型,主要用来探究双壳油船和中层甲板油船的阻漏效果。[8-9]由于Fr模型只考虑重力的相似,忽略黏性力的相似,不可避免地会产生缩尺效应。[8]此外,由于原油泄漏过程中存在流动变态行为,在舷侧破舱原油泄漏的密度差流阶段[10-11],油品泄漏的动力并非重力。在这种情形下,Fr模型就不能真实地反映原型的泄漏过程。
考虑到黏性力未相似会引发缩尺效应,文献[12]针对单壳油船原油泄漏情形,提出同时考虑重力和黏性力相似的Fr-Re模型。该缩尺模型是在满足Fr相似的前提下,选取特定黏度的油品进行试验,使模型的雷诺数与原型相等。当缩尺比较大时,难以找到黏度符合要求的油品[13],使得该模型具有一定的局限性,而且忽略了表面张力和浮力,采用该模型进行试验时可能会引发缩尺效应。
基于上述情况,首先对原油泄漏过程进行受力分析,确定影响原油泄漏的相关作用力。基于相似理论,对油舱原油泄漏过程进行量纲分析,推导出较为完整的相似准则数群,并据此建立3种不同的缩尺模型。在相同缩尺比下,通过对比分析3种缩尺模型的泄漏持续时间、泄漏速度和泄漏入海量等宏观泄漏特征参数,确定影响原油泄漏的主要作用力,最终得到建立缩尺模型必须依据的相似准则。
1 原油泄漏受力分析
双壳油船水下破舱原油泄漏是多种流动行为复合的过程。在不同损伤情形下,原油泄漏的主导力不同,且作用强度会随着泄漏过程的进行而发生改变。这里以静水环境中的双壳油船底部破舱泄漏情形为例,分析原油泄漏过程中的相关作用力。
图1为双壳油船原油泄漏示意,由于双层底空间的存在,从油舱中泄漏出的原油不会直接泄漏到外界,而是先泄漏到双层底中,随后穿透双层底过程中的水层泄漏到外界。[7]通常认为原油从油舱泄漏到双层底中的流动属于重力主导下的孔口出流,其流动行为还受黏性力和油-气表面张力的影响。[8]然而,在原油穿透双层底中的水层泄漏到外界的过程中,其还会受到浮力的作用。在这些作用力中,重力是驱动原油泄漏的力(动力),而黏性力、表面张力和浮力均是阻碍原油泄漏的力(阻力)。当某个作用力未按相同缩尺比缩小时,就会导致动力和阻力的相对大小发生变化,从而引发缩尺效应。
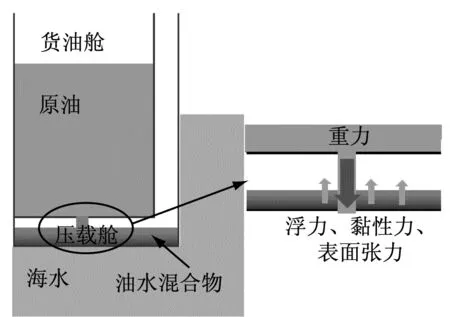
图1 双壳油船原油泄漏示意
2 缩尺模型的建立
目前已有研究采用的缩尺模型均未考虑表面张力和浮力。表面张力和浮力分别在油舱及双层底中起作用。这里以油舱为研究对象,针对原油从油舱泄漏到双层底的过程,采用量纲分析的方法推导出考虑表面张力的较为完整的相似准则数群,并据此建立缩尺模型。
2.1油舱油品泄漏量纲分析
内壳破孔处的原油泄漏平均速度v是衡量原油泄漏特征的重要指标。相关参数有油舱油位H,破孔孔径d,重力加速度g,油品密度ρ,油品动力黏度系数μ和表面张力系数σ。描述油舱油品泄漏速度的一般函数式为
f(v,H,ρ,g,d,μ,σ)=0
(1)
式(1)中:物理量的个数为n=7,采用[M],[L],[T]等3个基本量纲,m=3。根据π定理,这n个物理量的关系式可转换成n-m=4个无量纲量的函数关系式,即
f(π1,π2,π3,π4)=0
(2)
选择H,ρ,g等3个物理量作为基本物理量,其余4个参数可表示为
(3)
根据量纲一致性原理得到4个无量纲数,即
(4)
式(3)和式(4)中:π1为弗汝德数;π2为几何无量纲数;π3和π4分别可转换为雷诺数及韦伯数。弗汝德数、雷诺数和韦伯数分别是重力、黏性力及表面张力的相似准则。根据满足的相似准则个数的不同,可建立Fr模型、Fr-Re模型和弗汝德-雷诺-韦伯模型(以下简称Fr-Re-We模型)等3种缩尺模型。
2.2原油泄漏模型参数相似关系的导出
用m和p分别表示模型参数及原型参数。取几何比尺为λ=lp/lm,根据推导的相似准则导出模拟油舱原油泄漏过程的缩尺模型各参数与原型的相似关系。
1) 速度相似关系为vp=vmλ1/2。
2) 破孔孔径相似关系为dp=dmλ。
3) 油品动力黏度相似关系为μp=μmλρλ3/2。
4) 油品表面张力系数相似关系为σp=σmλρλ2。
5) 当模型的油品密度与原型相等时,动力黏度与表面张力系数相似关系分别简化为μp=μmλ3/2和σp=σmλ2。
根据几何相似关系和速度相似关系,可导出时间相似关系tp=tmλ1/2和油品体积相似关系Vp=Vmλ3。基于不同相似准则建立的不同缩尺模型主要比尺见表1。

表1 不同缩尺模型主要比尺
3 不同相似准则缩尺模型研究
选取的相似准则越合理,根据相似关系将缩尺模型试验结果反推回原型尺度得到的模型-原型结果与实际原型结果越接近。通过对比不同缩尺模型的油品泄漏特征参数与原型的偏差,即可判断出各相似准则的重要程度。参考相关研究[7],以某超大型油船的L型油舱边舱为模型舱原型,以Lone Rock原油为油品原型,根据表1设计缩尺模型试验。采用数值试验的方法模拟原型和各缩尺模型的油品泄漏过程。通过对比模型自由泄漏阶段持续的时间及油品泄漏入海量与原型的差异,探究油品泄漏过程中黏性力、表面张力和浮力的相对重要程度,进而确定建立缩尺模型时应采用的相似准则。
3.1缩尺模型试验设计依据
在缩尺模型试验中,模型缩尺比确定之后,可通过改变特征流速v和选取具有特定黏度μ的液体作为流体介质2种方法控制模型雷诺数Re=ρvd/μ。然而,在原油泄漏模型试验中,无法人为改变流速,只能通过选取具有特定黏度的油品控制模型的雷诺数。[13-14]同样,模型的韦伯数也通过改变油品的表面张力系数来控制。
3.2缩尺模型油品物性及模型几何参数的确定
小尺度缩尺模型试验的缩尺比通常为1:50~1:30,因此选取1:40作为缩尺模型的缩尺比。根据表1中的油品物性相似关系和模型几何特征相似关系,确定缩尺模型试验对照组的油品物性和模型几何参数(见表2)。此外,为探究浮力对油品泄漏的影响,设置试验油品密度和Fr-Re-We模型不同的对照组Fr-Re-We(D)。
为保证缩尺模型与原型的几何相似性,在原型和缩尺模型的几何模型中均忽略船壳厚度。简化的模型舱示意见图2。

a)正视图b)俯视图
图2 简化的模型舱示意
3.3研究方法及验证
该研究采用文献[15]给出的数值方法,经物模试验验证,该方法能较为准确地模拟油品泄漏过程。
3.4不同相似准则缩尺模型的试验结果
相似准则数反映各种作用力和惯性力的相对大小。根据Fr模型、Fr-Re模型、Fr-Re-We模型和Fr-Re-We(D)模型试验结果,分析黏性力、表面张力和浮力对原油泄漏的影响,从而确定缩尺模型试验应采用的相似准则。
3.4.1不同相似准则下的泄漏持续时间
理论上,当所有作用力都按相同比例缩小时,根据相似关系将缩尺模型结果反推回原型得到的结果应与原型相同。当某个相似准则未考虑(即某个作用力未按缩尺比缩小)时,缩尺模型转化到原型的结果会与原型产生偏差,该偏差就是该作用力未缩尺产生的缩尺效应。不同缩尺模型油品自由泄漏阶段持续时间见图3。从图3中可看出,Fr-Re模型和Fr-Re-We模型的泄漏持续时间与原型最为接近,Fr-Re-We(D)模型次之,Fr模型偏差最大。这说明黏度偏大、密度偏小会导致原油自由泄漏阶段持续时间偏短,黏性力和浮力是引发缩尺效应的主要原因。

表2 原油泄漏缩尺模型试验对照组

图3 不同缩尺模型油品自由泄漏阶段持续时间
Fr-Re-We模型是在Fr-Re模型的基础上考虑韦伯相似准则得到的缩尺模型。通过对比Fr-Re模型和Fr-Re-We模型可探究表面张力对原油泄漏的影响。图3中,2个缩尺模型的油品泄漏速度和油品从外壳破孔泄漏入海的平均速度均基本相同,说明在油品泄漏过程中表面张力的作用可忽略不计。
从图3~图7中可看出,Fr-Re模型和Fr-Re-We模型已能较为真实地反映原型,但仍存在偏差,这可能是未采用相应的相似准则对油水界面张力进行缩尺导致的。
Fr-Re模型是在Fr模型的基础上考虑雷诺相似准则得到的缩尺模型。通过对比Fr模型和Fr-Re模型可探究黏性力对原油泄漏的影响。图4为不同缩尺模型油舱油品泄漏平均速度。从图4中可看出,Fr模型中油品从油舱破孔泄漏进入双层底的平均速度略小于Fr-Re模型。这是因为Fr模型仅保证重力的相似,而黏性力未按相同比例缩小。当采用原油作为试验油品时,由于其黏度远大于黏性力相似应采用的油品黏度[10],导致油品在油舱中流动的阻力偏大,油舱油品泄漏平均速度偏小。

图4 不同缩尺模型油舱油品泄漏平均速度
在Fr模型中,油品进入双层底之后,由于油舱中的油品泄漏速度偏小,油射流所具备的动能不足以克服自身的浮力和水层的阻力,导致油品泄漏入海率远低于原型。此外,由于油射流不能占据外壳破孔,使得外界海水大量进入双层底。在这2方面的综合作用下,Fr模型的双层底液位上升速度远大于原型和其他缩尺模型,最终导致该模型自由泄漏阶段持续时间远小于原型。因此,黏性力是原油泄漏过程中的重要作用力,当黏性力未按相同比例缩小时,会导致缩尺模型自由泄漏阶段持续时间存在缩尺效应。这也说明在进行缩尺模型试验时,不能选取原油作为试验油品,而应根据雷诺相似准则选取特定黏度的油品。
Fr-Re-We(D)模型是在Fr-Re-We模型的基础上改变试验油品密度得到的缩尺模型。通过对比Fr-Re-We(D)模型和Fr-Re-We模型可探究浮力对原油泄漏的影响。图5为不同缩尺模型油品泄漏入海平均速度,2种模型的油舱油品泄漏速度基本相同,Fr-Re-We(D)模型的油品泄漏入海平均速度小于Fr-Re-We模型,与原型的偏差更大。
上述试验证明油品在穿透双层底中的油水混合物时会受到浮力的影响。当油品密度小于原油时,油品与海水的密度差变大,油品在油水混合物中流

图5 不同缩尺模型油品入海泄漏平均速度
动时受到的净浮力变大,油品泄漏入海的速度变小。泄漏入海速度变小意味着更多油品被保留在双层底中,双层底液位上升速度加快,自由泄漏阶段持续时间变短(如图3所示)。因此,浮力是油品泄漏过程中的另一个重要作用力,当其未按相同比例缩小时,会导致缩尺模型自由泄漏阶段持续时间存在缩尺效应。
由于油品密度发生改变,Fr-Re-We(D)模型的雷诺数并不与Fr-Re-We模型相同,但数值非常接近。然而,油品泄漏入海的速度与Fr-Re-We模型存在很大偏差,这说明仅保证雷诺数相同不能准确模拟原油在双层底中的流动行为。油品的密度和黏度是2个独立的影响因子,通过控制油品的运动黏度来控制雷诺数相同是不可行的。
3.4.2不同相似准则下的油品泄漏入海量
油品泄漏入海量是另一个重要的油品泄漏特征参数。不同缩尺模型自由泄漏阶段油品泄漏入海量见图6。从图6中可看出,Fr-Re模型和Fr-Re-We模型的泄漏入海量与原型最为接近,Fr-Re-We(D)模型和Fr模型的偏差均较大。这说明黏性力和浮力也会导致油品泄漏入海量存在缩尺效应。

图6 不同缩尺模型自由泄漏阶段油品泄漏入海量
油舱油品泄漏量取决于自由泄漏阶段持续时间和油品泄漏入海的平均速度。由于Fr模型未对黏性力进行缩尺,采用原油作为试验油品会导致油品泄漏平均速度偏小,自由泄漏阶段持续时间偏短。这2个参数偏小均会导致油舱油品泄漏量偏少(见图7)。

图7 不同缩尺模型油舱油品泄漏量
由于黏性力过大,使得油射流不能穿透双层底中的水层泄漏到外界,直接改变双层底中油水相互作用形式,导致模型油品泄漏入海量与原型存在巨大偏差(如图6所示)。这进一步证明要采用缩尺模型模拟原油泄漏过程,必须根据雷诺相似准则选取低黏度的油品作为试验油品。
在自由泄漏阶段,油舱中的油品与双层底中的油水混合物并未发生直接作用,浮力仅对双层底中的油品产生作用,因此Fr-Re-We(D)模型的油舱油品泄漏速度与Fr-Re-We模型基本相同。由于Fr-Re-We(D)模型采用的油品与海水的密度差更大,油品在双层底中流动时所受净浮力更大,油射流速度衰减更严重。因此,Fr-Re-We(D)模型的油品泄漏率偏小,双层底中油品积累的速度偏大,自由泄漏阶段持续时间偏短。虽然Fr-Re-We(D)模型油舱油品泄漏速度与Fr-Re-We模型相同,但Fr-Re-We(D)模型自由泄漏阶段持续时间更短,导致油舱泄漏量偏少。在油舱泄漏量和油品泄漏入海率均减小的情况下,Fr-Re-We(D)模型自由泄漏阶段的油品泄漏入海量偏少(如图6所示)。
综上所述,当模型中的油品所受的黏性力和净浮力偏大时,会导致自由泄漏阶段持续时间缩短,该阶段的油品泄漏入海量减少。然而,在进行缩尺物模试验时,较难使浮力和黏性力的大小同时满足相似准则的要求,这势必会导致自由泄漏阶段结束时的油品泄漏特征参数存在缩尺效应。若缩尺模型进入原油受阻泄漏阶段时的油舱油位和油舱油品泄漏速度(转化到原型尺度)与原型存在偏差,则受阻泄漏阶段的缩尺效应可能会被进一步放大。
4 结束语
针对原油自由泄漏阶段的油舱原油泄漏过程,基于相似理论,采用量纲分析的方法推导出完整的相似准则数群,并根据不同相似准则建立3种缩尺模型。通过数值试验的方法模拟相同缩尺比下不同缩尺模型的油品泄漏过程,根据相似关系将缩尺模型数值试验结果转换为原型尺度,将其与原型数值试验结果相对比,验证通过选取低黏度油品控制模型雷诺数的科学性。研究结果表明:
1) 黏性力和浮力是影响原油泄漏过程的重要作用力,这2个作用力未按相同缩尺比缩小是引发缩尺效应的主要原因。油-气表面张力在原油泄漏过程中可忽略不计。
2) 在进行缩尺物模试验时,应根据傅汝德相似准则建立缩尺模型,根据雷诺相似准则选取适当黏度的油品或尽量选取黏度小的油品,油品密度应与原油相等或接近,以降低缩尺效应的影响。
[1] HYSING T, TORSET O. Reduction of Oil Outflows at Collisions and Groundings Through Improved Vessel Design Arrangement[J]. Marine Pollution Bulletin, 1994, 29(6): 368-374.
[2] WIEL G V D, DORP J R V. An Oil Outflow Model for Tanker Collisions and Groundings[J]. Annals of Operations Research, 2011, 187(1): 279-304.
[3] 兰国新, 李颖, 刘丙新, 等. 基于多源遥感的海上溢油检测研究[J]. 中国航海, 2013, 36(1): 115-120.
[4] TAVAKOLI M T, AMDAHL J, LEIRA B J. Investigation of Interaction Between Oil Spills and Hydrostatic Changes[C]. ASME International Conference on Ocean, Offshore and Arctic Engineering, 2009: 803-811.
[5] TAVAKOLI M T, AMDAHL J, LEIRA B J. Analytical and Numerical Modelling of Oil Spill from a Side Tank with Collision Damage[J]. Ships and Offshore Structures, 2012, 7(1): 73-86.
[6] 赵卫斌, 卢金树, 朱哲野, 等. 油船水下破舱原油泄漏模型试验设计[J]. 浙江海洋学院学报(自然科学版), 2013, 32(3): 255-259.
[7] LU J S, LIU F C, ZHU Z Y. Effects of Initial Water Layer Thickness on Oil Leakage from Damaged DHTs[C]. The Twenty-Fourth International Ocean and Polar Engineering Conference, 2014: 618-625.
[8] KARAFIATH G. Accidental Oil Spill Due to Grounding: Summary of Model Test Results. Summary Report, Jan-Jun 92[R]. Bethesda, MD Naval Surface Warfare Center, 1992: 1-61.
[9] YAMAGUCHI K, YAMANOUCHI H. Oil Spills from the Double Hull Model Tanks[J]. Report of Ship Research Institute, 1992, 29: 1-38.
[10] 卢金树. 油船水下破舱油品泄漏动力学机理及特性研究[D]. 大连:大连海事大学, 2015:49-51.
[11] 卢金树, 刘枫琛, 吴文锋, 等. 破孔高度对油船水下破舱油品泄漏的影响[J]. 大连海事大学学报, 2015,41(2): 46-50.
[12] SIMECEK-BEATTY D, LEHR W J, LANKFORD J. Leaking Tank Experiments for Heavy Oils[J]. Beatty, 2012(1): 127-131.
[13] TAVAKOLI M T, AMDAHL J, LEIRA B J. Experimental Investigation of Oil Leakage from Damaged Ships Due to Collision and Grounding[J]. Ocean Engineering, 2011, 38(17): 1894-1907.
[14] SIMECEK-BEATTY D, LEHR W J, LANKFORD J F. Leaking Tank Experiments With Orimulsion and Canola Oil[J]. National Oceanic and Atmospheric Administration, 2003(12): 30.
[15] 卢金树, 刘枫琛, 朱哲野. 双壳油船底部破舱水下原油泄漏过程三维数值模拟[J]. 江苏科技大学学报 (自然科学版), 2014, 28(5): 423-428.
SimilarityCriteriaofPhysicalModelingforCrudeOilLeakagefromDoubleHullOilTanker
LUJinshu,WUHaoxiao,YANGZhenbo
(School of Maritime and Civil Engineering, Zhejiang Ocean University, Zhoushan 316022, China)
Laboratory investigation of oil leakage from double hull oil tank requires the selection of an adequate similitude. In order to ensure the rationality of the scale model tests, the dimension analysis method is used to deduce the similarity criteria that are required in the scale model test. Based on these similarity criteria, three different kinds of scale models are presented. Numerical simulation for the prototype and its 1/40 scale models based on different similitude criteria are carried out. According to the similarity criteria, the result from the scale model is extrapolated to the prototype flow conditions and compared with those directly calculated from the prototype. Based on the viscous fluid dynamics, the effects of viscous force, surface tensional force and buoyant force on the crude oil leakage process are analyzed. The results indicate that the Froude and Reynolds similarity criteria are the dominant similarity criteria and Weber criteria is negligible. When the density of oil used in the model is equal to that of crude, the scale effect is minimized. In different oil leakage stage, different scale model is required to simulate the oil leakage process.
ship engineering; scale model; similarity criteria; oil leakage; double hull oil tanker; viscous fluid dynamics
X55;U674.133.1
A
