不确定环境下的班轮运输补油策略与航速优化

张素庸， 汪传旭

(上海海事大学 经济管理学院,上海 201306)

2017-05-30

上海市科研创新重点项目(14ZS122)

张素庸(1992—)，女，安徽安庆人，硕士生，研究方向为航运物流。E-mail:soonchueng@foxmail.com

汪传旭(1967—)，男，安徽安庆人，教授，博士生导师，研究方向为供应链与物流管理。E-mail:cxwang18@aliyun.com

1000-4653(2017)03-0129-06

不确定环境下的班轮运输补油策略与航速优化

张素庸， 汪传旭

(上海海事大学 经济管理学院,上海 201306)

考虑燃油价格的不确定性及航运碳排放因素，以船舶加油港口的选择、补油量和各航段航速为决策变量，建立基于模糊规划的班轮运输船舶燃油补给策略与航速优化模型。从理论上分析论证该模型存在最优解，并运用实例验证模型的有效性。进一步分析燃油价格模糊区间大小、碳税税率对航运成本、船舶补油策略和航速决策的影响。结果表明：班轮企业只有合理设置燃油价格模糊程度和碳税税率，才能保证企业的经济效益和社会效益。

交通运输经济学；模糊规划；碳排放；补油策略；航速优化

随着经济贸易的迅速发展，水路运输已成为重要的货物运输方式，相较于其他运输方式，运输成本较低。目前航运企业面临的主要问题是如何在油价不确定的情况下降低燃油成本。由于航速大小直接影响船舶的耗油量，因此对补油量决策、加油港口的选择及航速决策进行研究具有重要意义。

目前，已有很多学者就航速问题展开一系列研究。ROMEN[1]得出耗油量与航速的三次方成正比，并据此建立航速优化模型。FAGERHOLT等[2]在单船单航线中研究航速优化问题，通过时间窗优化船舶航速。NORSTAD等[3]在已有研究的基础上将2个港口间的航速视为决策变量(即每个航段的航速度不同，相应的航行时间和航行费用也就不同)，建立费用最小化模型，据此确定航线的最优调度方案。DOUDNIKOFF等[4]建立最小化成本目标数，综合讨论硫排放控制区和非硫排放控制区的航速优化，并以北欧航线为例验证模型的适用性。WANG等[5]在假设航速是为满足集装箱转运需求而设定的前提下建立航速优化决策模型。

近年来，已有相关学者对船舶补油策略进行研究。刘天芸[6]提出对船用燃油成本实行事先、事中及事后管理的理念，以降低航运公司在运营过程中的燃油成本。WANG等[7]考虑到实际航速会偏离计划航速，建立混合非线性规划模型，进行补油决策；同时，证明燃油消耗与航速之间的关系及燃油消耗函数具有凸函数性质，运用逼近法求解模型，得出最佳补油策略。WANG等[8]利用 Fuzzy-Delphi-TOPSIS 方法及模糊德尔菲方法确定燃油价格，继而建立班轮公司补油港口的选择模型。

此外，也有相关学者综合补油策略和航速优化进行研究。YAO等[9]研究单航线航速和燃油决策，得出燃油购买量与航速之间的关系式，建立最优化模型进行航速和补油量的决策。黄涛[10]设计船舶燃油补给方案，研究燃油消耗与航速之间的关系，说明船舶以最佳航速运行可降低燃油成本。

这里以燃油价格为模糊数，综合考虑加油港口选择、补油量决策及航速决策，构建模糊规划模型。该研究与YAO等[9]的研究的区别在于：考虑燃油价格的不确定性和碳排放限额。

1 数学建模

1.1假设

在建立数学模型时，提出以下假设：

1)运力足够，不需要造船和租船。

2)船舶航线及挂靠港口的顺序已确定，按时进港、离港，不允许脱班。

3)所研究的班轮船型一致。

4)不考虑船舶在港口停留，以等待油价下降。

5)港口燃油供应可随时满足船舶需要。

1.2变量与参数

1)决策变量包括：航线r航段i的航速vri，n mile/h；航线r港口i的加油量xri；航线r港口i是否可加油Ari，Ari=0表示不加油，Ari=1表示加油。

1.3模型构建

1.3.1燃油成本

(1)

1.3.2碳排放成本

船舶排水量、主机功率和船舶航速之间存在一定的关系，可表示为

Ne=0.735 5D2/3v3/C

(2)

式(2)中：Ne为船舶主机功率，kW;D为船舶的排水量，t;v为船舶航速；C为海军系数。

船舶航行期间每小时的燃油消耗可表示为

G=10-6geNe

(3)

式(3)中：G为船舶航行期间每小时的燃油消耗；ge为船舶主机燃油油耗率，g/(kW·h)。

船舶在r航线i航段的燃油消耗量可表示为

(4)

引入HOEN等[11]提出的碳排放度量方法，即碳排放量 = 碳排放因子 × 燃油消耗量，其中碳排放因子为单位燃油的CO2排放量，表示船舶将燃油转化为碳排放的能力。根据SONG等[12]的计算，估计CO2排放因子为3.17，则船舶在航线r上往返的碳排放量为

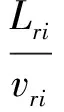
(5)

式(5)中：Lri为i航段的距离；pi为靠港停留时间；f1和f2分别为船舶副机在船舶航行及停泊时的燃油消耗率，t/h。若单位碳排放量碳税为δ，则碳排放成本为δQCO2。

1.3.3港口成本

由于并不是所有的港口都提供加油服务，因此当某港口不能提供补油服务时，船舶在该港口仅有燃油的消耗，将r航线i港口的加油量定义为xri，有

(6)

(7)

式(7)中：pi为单航次船舶在港口进行装卸作业及其他作业时所耗费的时间，h;pF为单船每小时的港口成本，美元/h。

1.3.4决策模型

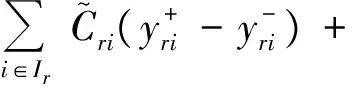
(8)

s.t.

∀r∈R， ∀i∈Ir

(9)

(10)

(11)

(12)

(13)

vmin≤vri≤vmax， ∀r∈R， ∀i∈Ir

(14)

(15)

ei≤Ti≤li， ∀r∈R， ∀i∈Ir

(16)

T1=0，Tn+1=168

(17)

Ari=1 or 0, ∀r∈R， ∀i∈Ir

(18)

式(8)～式(18)中：式(8)为总成本函数，包括补油成本、碳排放成本和港口成本；式(9)为油箱中的储油量最小要大于容量的4%；式(10)为油箱中的储油量最大不能超过自身容量；式(11)和式(12)为到达港口i时油量必须大于油箱容量的20%，小于油箱容量；式(13)为补油次数约束；式(14)为船舶航速约束；式(15)为船舶从i港口出发到达i+1港口的时间约束；式(16)为到达i港口的时间窗约束；式(18)为i港口是否可加油，1表示可加油，0表示不可加油。

2 模型的求解

2.1模糊规划模型的处理

采用三角模糊数描述模型中不确定的燃油价格，并用质心法将上述模型转化为模糊机会约束规划模型，以便求解。

MinZ

(19)

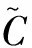
(20)

根据以上质心法可将目标函数和约束条件转化为

(21)

在各加油港口的燃油价格为隶属函数已知的三角模糊数的前提下将模糊变量非模糊化，继而用Lingo 11.0软件求解模型。

2.2最优解存在性的判定

为对上述模型进行求解，首先分析模型解的存在性。上述模型是典型的 0-1 非线性混合整数规划问题，不能对函数进行凹凸性判断，根据CHEN等[13]的研究，可将该模型转变为非线性混合整数规划问题。因此，目标函数和约束条件函数连续，可进一步对函数进行凹凸性判断，获得模型最优解，该解等同于转换前的最优解。

令uri=1/vri，则目标函数为

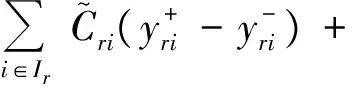
(22)

式(15)变为

1/vmax≤uri≤1/vmin， ∀r∈R， ∀i∈Ir

(23)

式(16)变为

Ti+Pi+Lriuri=Ti+1， ∀r∈R， ∀i∈Ir

(24)

定理1：目标函数z在Rn上是关于xri和uri的凸函数。

证明:目标函数分别对决策变量求一阶导数，得

对目标函数Z求二阶导数，有

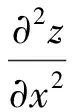
(27)

(28)

混合二阶导数均为0。目标函数Z的Hessian矩阵为

(29)

矩阵是半正定的，故目标函数是关于决策变量的凸函数。

定理2：约束条件都为凸函数。

认为决策变量的线性函数为凸函数，可看出关于uri的约束二阶导数之后大于零，显然约束都为凸约束。

由以上定理可知，该模型为凸规划，因此必有最优解。下面通过Lingo 11.0进行算例分析。

3 算例分析

以某航运公司的中日航线为例，验证上述数学模型和算法的合理性。该航线包含7个挂靠港口(见图1)。在该航线上，部署集装箱班轮来提供单周班服务。表1和表2为船舶相关参数取值。

图1 中日航线示意

表1 航段距离以及港口停留时间

表2 模型参数

表3 模型计算结果

由计算结果可知，总成本为793 761.5元，不同的航段有着不同的航速，同时补油港口的选择及补油量的决策也不相同，油价略低的港口的补油量明显高于油价稍高的港口。因此，该模型既可保证船舶日常的高效运转，又可使船舶航运成本最低。

4 灵敏度分析

4.1油价模糊区间灵敏度分析

在其他因素都不变的情况下，改变燃油价格模糊区间，分析燃油价格模糊区间的改变对船舶航运成本、补油量及平均航速的影响。

将区间由20扩大到22，24，26，28，30,32,34,36,38,40，分别观察区间扩大对航运总成本、航速和补油量的影响(见图2～图4)。

图2 模糊区间对航运成本的影响

图3 模糊区间对航速的影响

图4 模糊区间对加油总量的影响

由图2～图4可知：随着燃油价格模糊区间的增大，航运成本上升，船舶补油总量和平均航速先保持不变；当燃油价格模糊区间增大到34时，航速和补油量均下降。随着燃油价格模糊区间增大，油价的不确定性升高，因此航运成本上升，燃油价格对航运成本的影响非常显著。由于所研究的航速为经济航速，因此当燃油价格模糊区间不大时，平均经济航速可保持不变。当燃油价格模糊区间>34时，平均航速下降，配船数量增加，可能使航运成本增加，因此燃油价格的模糊程度不宜太大。

4.2碳税税率灵敏度分析

碳税税率变化必然影响船舶补油策略和航速决策，在假定其他各因素不变的情况下，通过改变碳税税率，分析航运成本、补油量和平均航速的变化(见图5～图7)。

图5 碳税税率对航运成本的影响

图6 碳税税率对航速的影响

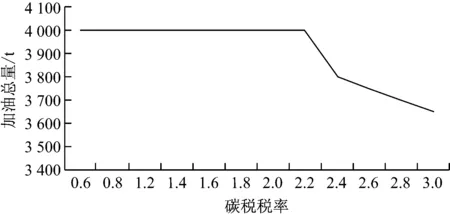
图7 碳税税率对加油总量的影响

由图5～图7可知：随着碳税税率的增大，航运成本依次上升，船舶补油总量和船舶平均航速先保持不变；当碳税税率增大至2.2时，船舶补油量和航速均下降。这说明碳税税率过低对减排效果并不明显，但碳税税率过高，航速降低，会使配船数量增加、航运成本上升，并会增加企业碳税过重的负担，因此合理制订碳税汇率尤为重要，不仅能保证企业的经济效益，而且可保护环境。

5 结束语

本文以低碳为背景，考虑燃油价格的不确定性，引入模糊变量，将船舶燃油成本、碳排放成本和装卸成本作为总目标函数，建立多港口单航线集装箱船舶补油和航速优化模型。以某航运公司的中日航线为例，分析燃油价格模糊区间及碳税税率对航速、成本和补油量的影响。下一步的研究方向：

1)在考虑单航线的补油决策和航速决策的同时，考虑多航线的决策。

2)考虑多种船型下的船舶航速和加油决策。

3)在考虑燃油价格的不确定性的同时，考虑船舶故障、港口拥堵等不确定因素。

[1] RONEN D. The Effect of Oil Price on the Optimal Speed of Ships[J]. Journal of the Operational Research Society, 1982, 33: 1035-1040.

[2] FAGERHOLT K, LAPORTE G, NORSTAD. Reducing Fuel Emission by Optimizing Speed on Shipping Routes[J]. Journal of the Operational Research Society, 2010, 61:523-529.

[3] NORSTAD I, FAGERHOIT K, LAPORTE G. Tramp Ship Routing and Scheduling with Speed Optimization[J].Transportation Research Part C, 2011,19:853-865.

[4] DOUDNIKOFF M, LACOSTE R. Effect of a Speed Reduction of Containerships in Response to Higher Energy Costs in Sulphur Emission Control Areas[J].Transportation Research Part D, 2014,28:51-61.

[5] WANG S, MENG Q, LIU Z.Container Ship Scheduling with Transit-Time-Sensitive Container Shipment Demand[J]. Transportation Research Part B, 2013, 54:

68-83.

[6] 刘天芸． 航运企业船舶燃油成本管理[J].世界海运，2007，29(6): 36-37．

[7] WANG Shuaian, MENG Qiang. Robust Bunker Management for Liner Shipping Networks[J].European Journal of Operational Research, 2015，243(3)：789-797.

[8] WANG Y Y, ADOLF G T. NG K Y. Choosing Optimal Bunkering Ports for Liner Shipping Companies: A Hybrid Fuzzy-Delphi-TOPSIS Approach[J].Transport Policy, 2014,35:358-365.

[9] YAO Z, NG S H, LEE L H. A Study on Bunker Fuel Management for the Shipping Liner Services[J]. Computers & Operations Research, 2012,39:1160-1172.

[10] 黄涛.船舶运输成本分析与控制[D].大连:大连海事大学，2002:23-40．

[11] HOEN K M R, TAN T, FRANSOO J C, et al. Effect of Carbon Emission Regulations on Transport Mode Selection in Supply Chain[M]. Berlin, Germany: Springer-Verlag, 2012.

[12] SONG D P, DONG J X. Flow Balancing-Based Empty Container Repositioning in Typical Shipping Service Routes[J]. Maritime Economics & Logistic, 2011,13(1):61-77.

[13] CHEN G, LIAO X. A Penalty Function Algorithm for Solving 0-1 Nonlinear Mixed Integer Programming[J].Comm on Appl Math and Comput, 2007, 21(1):110-115.

LinerShippingRefuelingStrategyandSpeedOptimizationUnderUncertainEnvironment

ZHANGSuyong，WANGChuanxu

(School of Economics and Management, Shanghai Maritime University, Shanghai 201306, China)

With the fuel price uncertainty and carbon emissions taken into account, the model for optimizing the liner shipping bunkering strategy and the speed is developed, which determines the bunkering ports, the bunkering amount and the speed of every leg of a voyage. Theoretical analysis proves the existence of the optimal solution to this model. A real example is given to illustrate the validity of the proposed model. The effects of the uncertain degree of oil prices and the carbon tax rate on refueling strategy and sailing speed are analyzed. The results show that the liner shipping enterprises should set up the fuzzy degree of fuel price and the carbon tax rate reasonably, in order to ensure the economic and social benefits of enterprises.

traffic transport economics; fuzzy programming; carbon emission; bunkering strategy; speed optimization

U676.3

A