介值定理的一种推广
2017-11-02胡茂林
胡茂林
(淮阴师范学院 数学科学学院, 江苏 淮安 223300)
介值定理的一种推广
胡茂林
(淮阴师范学院 数学科学学院, 江苏 淮安 223300)
利用区间套定理将闭区间上连续函数的介值定理推广到了更加一般的情况,给出了闭区间上仅有第一类间断点的函数的介值定理. 推广后的介值定理包含了原定理的情况, 在原定理的条件下仍是原定理的结论.
介值定理; 区间套定理; 闭区间
0 引言
介值定理[1,2]是闭区间上连续函数最基本的性质之一,在微积分学理论的形成与发展中具有非常重要的作用.介值定理、微分中值定理和积分中值定理可谓是微积分学中关于函数的中间值定理.关于微分中值定理和积分中值定理的各种证明及推广变形一直被广泛地研究和应用,例如,Abian[3]构造性地证明了罗尔中值定理,即不仅证明了满足定理结论中f′(ξ)=0的ξ的存在性,而且给出了寻求它的实际途经.宫兴隆[4]仿Abian证明罗尔中值定理的方法应用区间套定理证明了拉格朗日中值定理.李超[5]把微分中值定理推广到了开区间内存在不可导点的情形.郑权[6]把有关积分中值定理中间点的渐近性的结果,推广到了更加一般的情形.赵益坤等[7]人更是讨论了曲线积分中值定理中间点的渐近性.而关于介值定理的推广变形研究则较为鲜见.鉴于介值定理本身在微积分学中的重要地位及在证明积分中值定理时的重要作用,有必要考虑这一定理的更加一般的形式.因此,本文试图把闭区间上连续函数的介值定理推广到闭区间上仅有第一类间断点的函数的情形.
本文中的f(x0-0)表示函数f(x)在点x0处的左极限,f(x0+0)表示函数f(x)在点x0处的右极限;U-(ξ;ε)=(ξ-ε,ξ],U+(ξ;ε)=[ξ,ξ+ε).对于其他熟知的概念、性质和记号参阅文[1].
1 介值定理的推广及其证明
引理1 若ξ∈[an,bn](n=1,2,…)是区间套{[an,bn]}所确定的点,则对任给的ε>0,存在正整数N,使得当n>N时有an∈U-(ξ;ε),bn∈U+(ξ;ε).
证明由于ξ∈[an,bn](n=1,2,…)是区间套{[an,bn]}所确定的点,则由区间套定理的推论[1],对任给的ε>0,存在正整数N,使得当n>N时有[an,bn]⊂U(ξ;ε);又由于数列{an}单调增收敛于ξ,数列{bn}单调减收敛于ξ,因此当n>N时有an∈(ξ-ε,ξ],bn∈[ξ,ξ+ε),即an∈U-(ξ;ε),bn∈U+(ξ;ε).
引理2 设函数f(x)在闭区间[a,b]上仅有第一类间断点,那么
(i) 若f(a+0)>0,f(b-0)<0,则存在ξ∈(a,b)使得f(ξ+0)≤0≤f(ξ-0);
(ii) 若f(a+0)<0,f(b-0)>0,则存在ξ∈(a,b)使得f(ξ-0)≤0≤f(ξ+0).
证明仅证(i).
由于函数f(x)在闭区间[a,b]上仅有第一类间断点,则对于任意的x∈[a,b],当x∈(a,b)时,f(x-0)与f(x+0)都存在;当x=a时,f(a+0)存在且f(a+0)>0;当x=b时,f(b-0)存在且f(b-0)<0.为方便另记[a,b]为[a0,b0].
现将[a,b]等分成两个子区间[a,c0]与[c0,b].若f(c0-0)≥0且f(c0+0)≤0,则c0即为所求之ξ;否则必有f(c0-0)<0或f(c0+0)>0,则当f(c0-0)<0但f(c0+0)≤0时记[a1,b1]=[a,c0],当f(c0-0)≥0但f(c0+0)>0时记[a1,b1]=[c0,b],而当f(c0-0)<0且f(c0+0)>0时在[a,c0]与[c0,b]中任取一个记为[a1,b1].于是有
f(a1+0)>0,f(b1-0)<0,
且
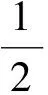
再从区间[a1,b1]出发,重复上述过程,或者在[a1,b1]的中点c1处有f(c0-0)≥0且f(c0+0)≤0,或者得到闭区间[a2,b2],使得f(a2+0)>0,f(b2-0)<0,且
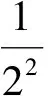
将上述过程不断地进行下去,必然出现以下2种情形:
1) 在某一区间[ai,bi] (i=0,1,2,…)的中点ci处有f(ci-0)≥0且f(ci+0)≤0;
2) 在每个区间[an,bn] (n=0,1,2,…)的中点cn处均有f(cn-0)<0或f(cn+0)>0,则得到闭区间列{[an,bn]},满足f(an+0)>0,f(bn-0)<0,且
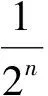
当出现情况1)时,取ci=ξ,则命题得证.
当出现情况2)时,闭区间列{[an,bn]}是区间套.由区间套定理,存在点ξ∈[an,bn](n=0,1,2,…).
下面用反证法证明情况2)中的ξ满足f(ξ-0)≥0且f(ξ+0)≤0.
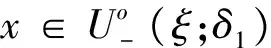
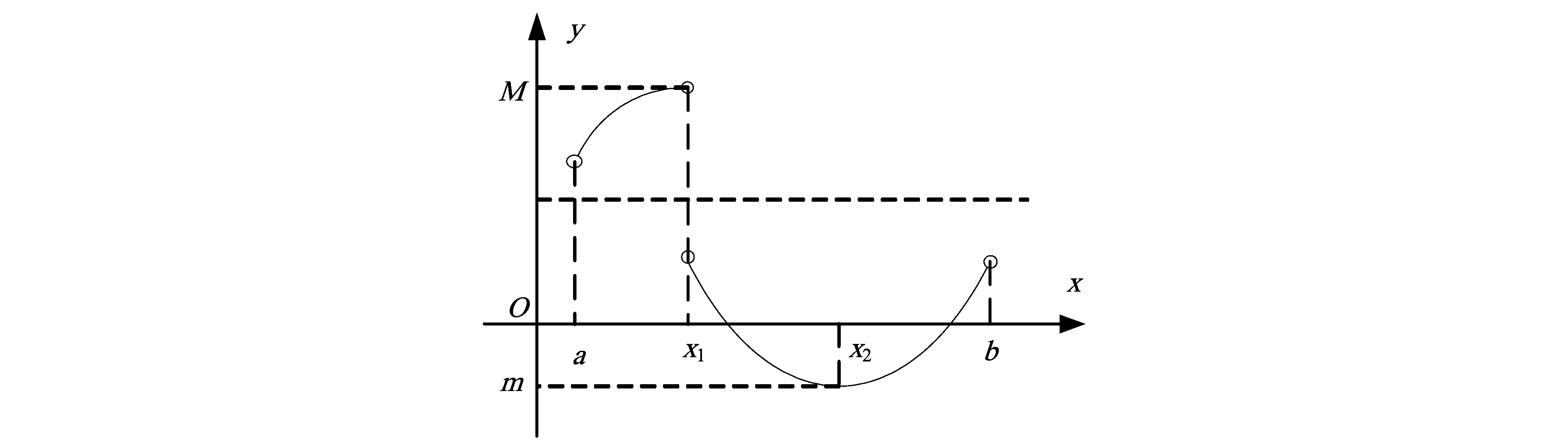
定理1(推广形式1) 设函数f(x)在闭区间[a,b]上仅有第一类间断点,且f(a+0)≠f(b-0).若μ为介于f(a+0)与f(b-0)之间的任何实数,即f(a+0)>μ>f(b-0)或f(a+0)<μ f(ξ+0)≤μ≤f(ξ-0)或f(ξ-0)≤μ≤f(ξ+0). 证明令g(x)=f(x)-μ.由题设易知函数g(x)在闭区间[a,b]上仅有第一类间断点, 且有g(a+0)>0,g(b-0)<0或g(a+0)<0,g(b-0)>0.再由引理2知,存在ξ∈(a,b),使得 g(ξ+0)≤0≤g(ξ-0)或g(ξ-0)≤0≤g(ξ+0), 即 f(ξ+0)≤μ≤f(ξ-0)或f(ξ-0)≤μ≤f(ξ+0). 定理2 设函数f(x)在闭区间[a,b]上仅有第一类间断点,且f(a+0)·f(b-0)<0,那么存在ξ∈(a,b)及非负实数h,k满足h+k=1使得 hf(ξ-0)+kf(ξ+0)=0. 证明不妨设f(a+0)>0,f(b-0)<0,由引理2知存在ξ∈(a,b)使得f(ξ-0)≥0,f(ξ+0)≤0. 若f(ξ-0)>0或f(ξ+0)<0,则取非负实数 使得h+k=1而且有 定理3(推广形式2) 设函数f(x)在闭区间[a,b]上仅有第一类间断点,且f(a+0)≠f(b-0).若μ为介于f(a+0)与f(b-0)之间的任何实数,即f(a+0)>μ>f(b-0)或f(a+0)<μ 证明由题设f(a+0)>μ>f(b-0)或f(a+0)<μ 推论1 设函数f(x)在闭区间[a,b]上仅有第一类间断点,且左、右极限存在最大值、最小值:M=max{f(x-0),f(x+0)|x∈[a,b]}与m=min{f(x-0),f(x+0)|x∈[a,b]}(m 证明不妨设存在x1,x2∈(a,b)且x1 M=max{f(x1-0),f(x1+0)},m=min{f(x2-0),f(x2+0)}, 则有下列几种情况: 1)M=f(x1+0),m=f(x2-0); 应用定理3到区间[x1,x2],命题便可得证. 2)M=f(x1-0),m=f(x2-0). 对于介于m与M之间的任何实数μ(m<μ 当f(a+0)<μ 当m<μ 当μ=f(a+0)时,考察f(x1+0)的值: 若f(x1+0)>μ,则应用定理3到区间[x1,x2]上,命题便可得证; 若f(x1+0)=μ,则取h=0,k=1,就有hf(x1-0)+kf(x1+0)=0·M+1·μ=μ,即x1为所求之ξ; 若f(x1+0)<μ,则取 这时h>0,k>0,h+k=1且 即x1为所求之ξ. 3)M=f(x1+0),m=f(x2+0).仿2)可证. 4)M=f(x1-0),m=f(x2+0). 不妨设f(a+0) f(a+0)<μ 对于前2种情况f(a+0)<μ 而当m<μ 推广后的介值定理包含了原定理的情况,在原定理的条件下仍是原定理的结论.另外,介值定理还可以表述为:“设函数f(x)在闭区间[a,b]上连续,x1 图1 推广后的介值定理的介值点ξ=x1∈(a,b) [1] 华东师范大学数学系. 数学分析[M].3版.北京:高等教育出版社,2001. [2] 菲赫金哥尔茨. 微积分学教程[M].徐献瑜,冷生明,梁文骐,等,译.北京:人民教育出版社,1959. [3] Abian A. A ultimate proof of Relle's theorem[J]. Amer Math Monthly,1979(86):484-485. [4] 宫兴隆. 拉格朗日中值定理的一个证明[J]. 数学通报,1982(12):31-32. [5] 李超. 开区间内有不可导点的微分中值定理[J]. 大学数学,2007,23(2):147-150. [6] 郑权. 积分第一、二中值定理的中间点的渐近性质的一般性定理[J]. 数学的实践与认识,2005,35(5):240-243. [7] 赵益坤,节存来,王磊. 关于曲线积分中值定理“中间点”的一个一般性结果[J].大学数学,2007,23(1):166-169. AGeneralizationofIntermediateValueTheorem HU Mao-lin (School of Mathematics Science, Huaiyin Normal University, Huaian Jiangsu 223300, China) In this paper, we generilize the intermediate value theorem for continuous functions on compact intervals in R to a wider range by using theorem of nested interval, and give the intermediate value theorem for functions with only discontinuity points of the first kind on compact intervals. intermediate value theorem; theorem of nested interval; compact intervals O172.1 A 1671-6876(2017)03-0210-04 [责任编辑李春红] 2017-01-13 胡茂林(1963-), 男, 宁夏固原人, 教授, 研究方向为组合优化. E-mail: humaolin2000@163.com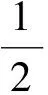
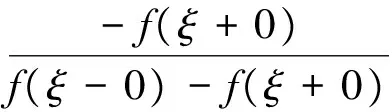
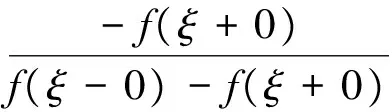


2 小结