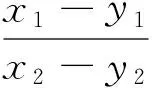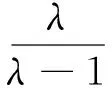两类数列不等式的证明探析

彭耿铃

福建省泉州市第七中学 (362000)

两类数列不等式的证明探析

彭耿铃

福建省泉州市第七中学 (362000)

不等式的证明因其思维跨度大、构造性强，需要有较高的放缩技巧而充满思考性和挑战性，能全面而综合地考查学生的后继学习潜能，因而成为高考试题考查的极好素材，倍受青睐.本文就此类题目进行总结梳理，希望读者能决胜于高考.

一、对数型数列不等式的证明探析

例1 (2014年陕西理科卷)设函数f(x)=ln(1+x),g(x)=xf′(x)(x≥0)，其中f′(x)是f(x)的导函数．

(Ⅰ)令g1(x)=g(x),gn+1(x)=g(gn(x))(n∈N+)，求gn(x)的表达式；

(Ⅱ)若f(x)≥ag(x)恒成立，求实数a的取值范围；

(Ⅲ)设n∈N，比较g(1)+g(2)+…+g(n)与n-f(n)的大小，并加以证明．

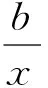
(Ⅰ)用a表示b,c；

(Ⅱ)若f(x)≥lnx在[1,+∞)上恒成立，求a的取值范围；

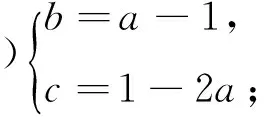
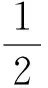
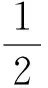
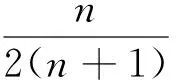
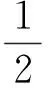
小结：在证明对数型数列不等式，其常用的证明方法是设数列不等式的左、右两边分别为Sn、Tn，只要控制Sn的通项an大于或小于Tn的通项bn即可，而证明an>bn(an

二、常数形数列不等式的证明探析

例3 (2014年新课标全国Ⅱ卷)已知数列{an}满足a1=1,an+1=3an+1.

(Ⅰ)若x1,x3,x5成等比数列，求参数λ的值；

总结：在证明常数形数列不等式，其常用的证明方法是构造一个小于或大于不等式的右边常数的数列和Tn，只要控制不等式左边的通项an大于或小于Tn的通项bn即可.