“偿二代”下我国保险监管的博弈分析

王毓雯 山东财经大学保险学院

“偿二代”下我国保险监管的博弈分析

王毓雯 山东财经大学保险学院

如何加强保险业的监管，使其健康有序地发展，一直是我国保险业的一个热点话题。通过以博弈论作为工具来分析保险监管，可以清楚地了解保险公司与监管机构在监管过程中的策略选择，找出能够影响保险公司和监管机构行为选择的关键因素，从中分析得到保险监管部门提高监管效率的有效措施，从而为制定完善的监管政策提供参考建议，以实现进一步规范和管理保险市场的目的，使我国保险业能够健康有序地快速发展。

一、引言

2016年1月，“偿二代”正式实施。“偿二代”要求保险企业按季度披露偿付能力，2016年各保险公司一季度的偿付能力备受关注。据相关报道，约七成的保险公司偿付能力出现下滑，但下滑程度不尽相同。“偿二代”更加全面科学地计量了保险行业的风险，进而使整个行业抵御风险的能力不断增强。在以风险为导向的“偿二代”体系下，对资产负债不匹配、业务质量较差、承保风险较大的保险公司来说，资本要求会进一步提高。在“偿一代”下可能被掩盖的激进投资、风控体系形同虚设等顽疾，将在“偿二代”下暴露无遗。

因此，如何进行成本合理、强度适中、有效率的保险监管，有效地保护保险消费者的利益，提高我国保险业的国际竞争力，推动我国保险业的长期可持续发展，是当前和今后保险监管面临的一个重大课题。本文运用静态博弈模型，探讨保险监管过程中保险公司与监管机构的博弈选择。

博弈论是研究行为策略的重要方法，将博弈模型应用到保险领域，可以充分了解保险利益相关者的策略选择。胡继华（2010）构建了社会保险待遇发放中监管者和待遇领取者之间的混合策略博弈模型，并求出监管者和待遇领取者之间博弈时各自的最优选择。陈利、谢家智（2013）构建了包括政府、保险公司、合作组织和农户在内的保险主体参与的合作机制，运用Shapley Value分析了农业保险主体的联盟博弈。卓志、邝启宇（2014）构建了一个包括政府、保险公司、消费者三方的巨灾保险市场的演化博弈模型，基于前景理论刻画了消费者价值函数。王茂琪、陈秉正（2014）从双人博弈模型入手，构建了新的包含保险人、投保人和监管者三方的博弈模型，从而更为准确地反映了保险市场主要参与者之间的相互关系，以及监管行为对市场各方参与者的影响。周晶（2014）根据进化博弈的思想和方法，在有限理性框架下构建保险监管机构间的非对称博弈模型，发现监管收益和监管成本是造成监管不同步及监管漏洞的重要原因。李文中（2014）基于博弈论对小额贷款保证保险面临的逆向选择和道德风险进行研究。刘峰（2014）基于对不同环节下博弈研究的结果得出，社会保险基金在监管实践中应坚持适度性、成本—收益最大化等原则，并就加强和完善中国社会保险基金在不同环节下的监管提出相关建议。刘思佳（2016）从存款保险制度中各个构成主体相互博弈的角度诠释对该制度实施的观点和看法，分析存款保险制度的可行性以及可能诱发的新问题，并提出相关建议。

二、我国“偿二代”下保险监管的基本现状

以风险为导向的“偿二代”可以说是我国保险业的一场革命，是我国监管机构向欧美等发达国家的成熟监管制度看齐的重要举措，有利于我国不断提升风险管控能力和公司治理水平，而且将倒逼国内保险业转型升级，从粗放型的规模增长转为集约型的精耕细作。

“偿二代”整体框架由制度特征、监管要素和监管基础三大部分构成。其中，监管要素是偿付能力监管的三大支柱，是偿付能力监管的重要组成部分。三大支柱分别从定量资本要求、定性监管要求和市场约束机制三个方面对保险公司的偿付能力进行监督和管理，主要规范偿付能力监管的内容、原则、方法和标准。第一支柱定量监管要求，主要防范能够用最低资本量化的保险风险、市场风险和信用风险，通过科学地识别和量化上述风险，要求保险公司具备与其风险暴露相匹配的资本。第二支柱定性监管要求，是在第一支柱的基础上，进一步防范难以量化的风险，如操作风险、战略风险、声誉风险、流动性风险等。我国保险市场是一个新兴市场，采用定量监管手段来计量这些风险存在较大困难，因此，需要更多地使用第二支柱的定性监管手段来评估和防范。第三支柱市场约束机制，即在第一支柱和第二支柱基础上，通过公开信息披露、提高透明度等手段，发挥市场的监督约束作用，防范依靠常规监管工具难以防范的风险，具体包括保险公司偿付能力信息公开披露、监管部门与市场相关方的偿付能力信息交流、信用评级等三大监管工具。

三、我国保险监管的静态模型分析

（一）模型的假设

1.参与人。为了简化问题，本文假定该博弈模型中有两方参与人：局中人1设定为保险监管机构，局中人2设定为保险公司。假设局中人都是风险中性的理性人，能够合理利用自己的有限资源来为自己争取最大的效用和利润。

2.行动。假设局中人1有两种博弈策略的选择，一种是采取监管的策略，另一种是不监管的策略，在此情况下监管机构的策略集为A1={监管，不监管}；而局中人2也有两种博弈策略的选择，即合法运营和违法运营，它的策略集为A2={合法运营，违法运营}。在保险监管的全过程中，博弈双方的行动均不分先后顺序，假设它们同时对自己的行为作出决策选择，也就是展开静态博弈的过程。

（二）模型的建立

首先，要根据现实情况，对保险监管过程中博弈双方可能采取的不同策略进行分析，对不同策略选择下需要付出的成本以及可能获得的收益分别进行参数设定。

对于保险公司来说，如果其选择合法运营的策略，则可以获得正常收益Y（Y＞0）；如果其进行违法运营，则保险公司可以获得一个额外的收益Y′（Y′＞0）；如果保险公司违法运营，而监管机构进行严格监管，并发现了保险公司的违法行为，则保险公司除了被罚没正常收益 Y和额外收益Y′，还会受到一个额外的罚款F（F＞0）。

对于监管机构来说，当它不监管时，无需付出任何努力，则它的实际成本为0；而进行监管时，它的成本增大为C（C＞0）。假设监管机构可以取得的正常效用为U（U＞0），此时保险合法运营，而监管机构不监管，则监管者只能得到正常的效用。另外，如果监管机构发现保险公司违法运营则可以获得来自外部的额外奖励P（P＞0）；相反，如果保险公司违法运营时，监管机构监管不力，并没有发现保险公司的违规行为，则监管机构要受到严重的惩罚D（D＞0）。

在此基础上，本文建立了保险公司和监管机构在完全信息下的静态博弈模型，如表2所示。

由表2可知，当监管机构进行监管时，保险公司的最优策略是合法运营；当监管机构不监管时，保险公司的最优策略是违法运营。当保险公司进行合法运营时，不进行监管是监管机构的最优策略；而当保险公司违法运营时，监管机构的最优策略是U+P-C和U-D中的较大值。

▶表1模型参数的设定和含义

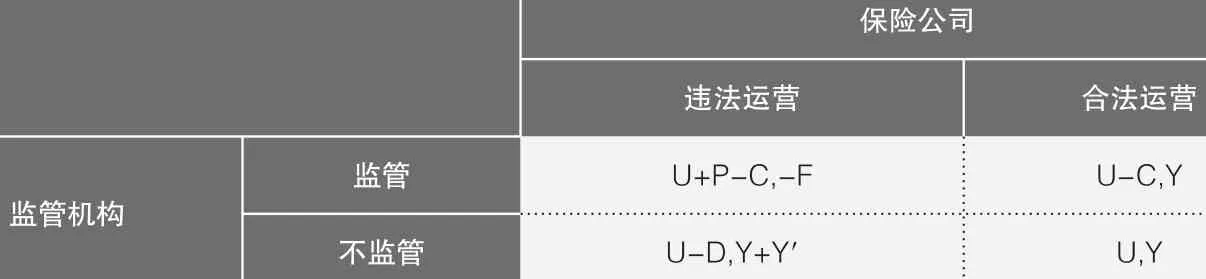
▶表2保险监管完全信息静态博弈模型

（三）模型均衡求解

运用博弈论中的划线分析法来分析该模型，可知当U+P-C＜U-D时，即P+D＜C时，该博弈的纳什均衡是{不监管，违法运营}。对于这样一种均衡结果，从经济学方面理解，它可以表述为，监管机构进行监管时需要付出的成本太高，远远大于其进行监管时所获奖励与监管不力时遭受的惩罚的总和。在这种情况下，监管机构没有足够的动力去进行监管，因为成本远远大于收益，所以从理性人的角度出发，这是一个没有效率的均衡。

当U+P-C＞U-D时，即P+D＞C时，用箭头分析法分析该博弈模型，该博弈会陷入“监管机构进行监管→保险公司合法运营→监管机构不监管→保险公司违法运营→监管机构进行监管”的无限反复循环中，所以博弈双方的最优策略是不能确定的，双方会以一定的概率从策略集中进行选择，而且从博弈目的的角度而言，这个行为的概率绝对不能让对方占优，因此这是一个混合策略均衡的问题。

假设监管机构采取监管策略的概率为p（0≤p≤1），则不进行监管的概率为1-p；同时假设保险公司违法运营的概率为q（0≤q≤1），则合法运营的概率为1-q。根据上述假定，可以得到监管机构和保险公司的期望收益函数。

监管机构进行监管的期望效益函数是：

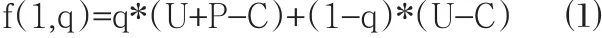
监管机构不进行监管的期望效益函数是：

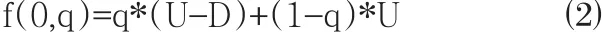
保险公司进行合法运营的期望效益函数是：

保险公司进行违法运营的期望效益函数是：

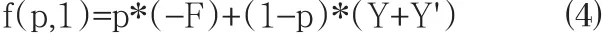
下面采用支付等值法求该博弈模型的混合策略均衡，令保险机构合法运营与违法运营的期望效益函数相等，即

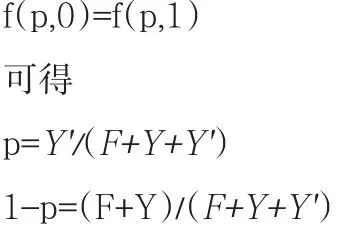
根据上述分析，当监管机构监管的概率大于均衡概率Y'/（F+Y+Y'）时，保险公司合法运营所获得的收益严格大于违法运营获得的收益，因此，此时违法运营策略是严格劣于合法运营策略的。由此推断出，如果监管机构加大自身的监管力度，客观上提高进行严格监管的概率，那么保险公司进行违法运营的可能性就会降低。相反，当监管机构进行监管的概率小于均衡概率Y'/（F+Y+Y'）时，保险公司的最优策略选择是进行违法运营。而如果监管机构采取监管策略的概率正好等于均衡概率Y'/（F+Y+Y'），那么对于保险公司来说，违法运营与合法运营所取得的效益相同，也就无所谓选择哪一种策略了。

下面，令监管机构进行监管的期望效益函数与不监管的期望效益函数相等，即

f（1,q）=f（0,q）

可得

q=C/（P+D）

1-q=（P+D-C）/（P+D）

对于保险公司来说，当它以小于C/（P+D）的概率进行违法运营时，监管机构的最优策略是不进行监管，因为不监管所获得的效益高于监管时所获得的效益；而当保险公司违法运营的概率大于C/（P+D）时，进行监管则成为监管机构的最优策略；当保险公司违法运营的行动概率等于C/（P+D）时，对于监管机构来说，无论是监管还是不监管，所获得的效益相同，因此监管机构对监管的态度变得无所谓。

综上所述，本博弈的混合策略均衡解是{p=Y'/（F+Y+Y'）,q=C/（P+D）}，即监管机构采取监管策略的概率为Y'/（F+Y+Y'），这一概率值也可理解为监管机构对Y'/（F+Y+Y'）比例的保险公司进行监管；而保险公司采取违法经营策略的概率为C/（P+D），这一概率可进一步理解为采取违法经营的保险公司的比例。

（四）模型结果分析

要想降低保险公司违法运营的概率C/（P+D），可以从两方面入手：第一，使分子C减小，即尽可能减少监管机构进行监管时耗费的成本。第二，使分母中的P和D增大，即对于认真履行监管职能的工作人员，采取一定的奖励措施；而对于失职的工作人员，要加大惩罚力度。

为了提高监管的效率，同时让监管保持在一个较高的水平，就必须尽可能地降低概率Y'/（F+Y+Y'）的值。一种方法是，可以让分子尽可能地减小，也就是降低保险公司违法运营所能获得的额外收益Y′，但是这是不可控的；因此要实施第二种方法，增大分母，即增加对保险公司违法运营时的罚款数额F和合法运营时所能获得的正常收益Y。

四、结论与建议

从对本文博弈模型的具体分析中可以看出，保险公司出于自身对于短期利益的追求，有可能进行违法运营；而保险监管机构也有可能出于自身利益最大化的选择，对监管工作玩忽职守，因此不能有效地对保险公司的运营进行监督和管理。

而保险公司进行违法运营的行为主要受监管机构的影响，它取决于监管机构的监管水平，具体来说，监管机构进行监管的成本越大，监管机构越趋向于不监管，所以保险公司越有可能进行违法经营；监管机构执行监管时所能够获得的奖励额度如果够大，会激励监管机构进行严格监管，迫使保险公司不敢从事违法运营；监管机构玩忽职守时所受到的惩罚力度越大，越能激励监管机构切实履行监管职能。

另一方面，影响监管机构策略选择的因素主要有：保险公司违法运营获得的额外收益额越大，越会促使保险公司违法运营，此时监管机构更趋向于认真、严格的监管；保险公司被查出违法运营时所受到的惩罚力度越大，越能约束保险公司的行为，从而会使监管机构采用一般的普通监管策略。

根据上述结论，本文基于博弈论的视角对完善我国保险监管提出以下几点建议：

第一，建立和完善保险公司的内控机制，强化公司内部监管和加快内控机制建设；健全财务制度，加强资金运用管理；提高承保理赔质量，规范业务操作程序；加强对保险代理营销市场的管理。

第二，建立和完善保险行业自律组织，充分发挥其市场监管的补充作用。作为保险行业自律组织的保险行业协会，既是政府与保险业的中介、国家监管的有力助手，又是保险监管体系中不可缺少的重要组成部分，它能够切实提高各保险公司参与市场管理的自觉性。

第三，稳妥有序地组织“偿二代”实施，不断完善保险监管。按照“十三五”规划，完善保险业审慎监管体系；跟踪完善“偿二代”标准，发布“偿二代”配套标准，通过监管升级推动行业转型升级，服务经济社会新常态发展；继续做好保险公司偿付能力状况的监测、分析、预警等工作，做好风险防范，守住风险底线