对立体几何找直线与平面交点问题的探究
2017-11-01田炜歌
田炜歌
对立体几何找直线与平面交点问题的探究
田炜歌
立体几何基础知识体系的建构是一个循序渐进的过程,学生对其基本定理和公理的理解程度决定了解题和判断能力。很多学生到了高三阶段在立体几何问题中举步维艰,其实是源于基础知识的缺失。本文以2016年高三质量检测考试中的一道立体几何试题为例,探究直线与平面交点的方法,希望对巩固学生的立体几何知识、提升空间想象和推理论证的能力,为教师进行立体几何教学和高三复习提供帮助。
立体几何;交点;公理;定理
一、发现问题
在2016年9月的长春市高三质量检测(一模)考试中,文科数学16题是一道考查学生空间想象能力的立体几何试题:已知三棱锥S-ABC,满足SA,SB,SC两两垂直,且SA=SB=SC=2,Q是三棱锥S-ABC外接球上一个动点,则点Q到平面ABC的距离的最大值为多少?

图(1)
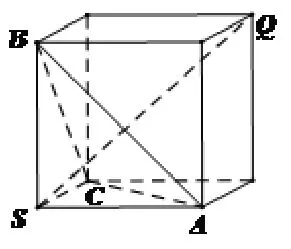
图(2)
此题的得分率不高,是因为学生习惯性地先画如图(1)所示的三棱锥,这就很难求出外接球的特征。当提示要观察三垂足S,并把三棱锥S-ABC还原成立方体之后,学生们很快就能发现三棱锥的外接球就是立方体的外接球,外接球的球心即立方体的中心,到平面ABC距离最大时点Q的位置如图(2)所示,在顶点S所在的体对角线的另一端。
但是5分钟后,学生仍然没能得出结论,其原因不是SQ为什么垂直于平面ABC,而是提出了另外一个问题:SQ与平面ABC的交点在哪里?
这个问题很好回答,也有多种方法去解决,其应用的是立体几何中的基础知识,但却成为了学生解题的绊脚石。这说明学生的空间想象能力较弱,对直线与平面垂直的判定定理和性质定理的综合应用能力弱,对最基本公理的理解也不到位。
二、探究问题
以此题为例,介绍三个方法来解决这个“找交点”问题。
方法一:从外接球的角度讲,直径SQ垂直于球的截面ABC,这个垂足K就是△ABC外接圆的圆心。去掉干扰线,应如图3所示。

图(3)
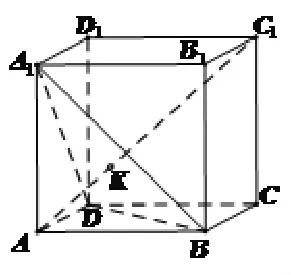
图(4)
方法二:人教A版教材中,习题B组中有原题,求证立方体ABCD-A1B1C1D1中,直线AC1与平面A1BD的交点是△A1BD的重心。利用射影定理,因为 AB=AD=AA1,所以 KD=KB=KA1,所以得点K是△A1BD的外心,即为正△A1BD的重心。如图4所示。
方法三:利用公理进行作图求得交点K。如图5所示,连接SD交AC于点M,连接BM。因为 K∈SQ且 SQС 平面 SBQD,所以 K∈面SBQD,所以K是平面ABC与平面SBQD的公共点,所以位于平面ABC与平面SBQD上的交线上;又因为点B,M都在平面ABC与平面SBQD上,所以线BM即为平面ABC与平面SBQD的交线,所以点K在交线BM上;综上,直线SQ与直线BM的交点即为直线SQ与平面ABC的交点K。
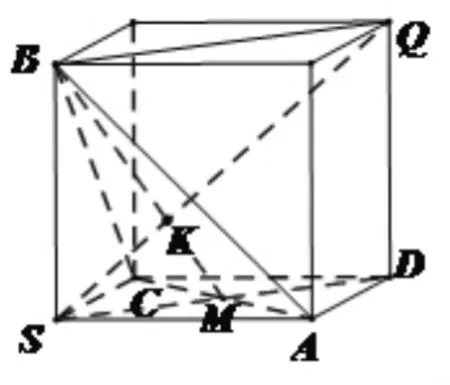
图(5)
三、比较三个方法得出找交点的通法
方法一要求学生有很好的空间想象能力,这个思路以球为载体,在复习必修2第一章旋转体的部分时,借助正方体的外接球模型来认识球是一个空间的几何体,让学生熟知球的截面是圆,过球面上任意三个点A、B、C做的截面都是圆,即△ABC的外接圆。
方法二是考查射影定理模型,新教材中,不提倡射影定理及其逆定理,而是直接用直线与平面垂直的判定定理和性质定理来理解这个模型。在复习必修2第二章直线与平面垂直的判定定理与性质定理时,让学生对这个模型深入理解。通过这道题或正三棱锥为载体来了解掌握射影定理模型,并通过这个模型来进一步理解直线与平面垂直的判定定理和性质定理。
方法三是最基础的方法,只使用公理1与公理3即可。公理1的作用是判定直线在平面内,公理3的作用最常用来证明三点共线或三线共点,教材中能够作为理解这两个定理的题很少,本题恰恰提供了一个很好的思路,并且适用于所有类似的找交点问题。
为了能提高学生在立体几何上的综合能力,加强对公理的理解与使用,教学时,笔者先要求学生背诵一遍三个公理的内容,并给出以下三个“找交点”问题。
题1:已知长方体 ABCD-A1B1C1D1,如图 6,底面ABCD边长1,高 AA1长2,求BD1与面B1AC的交点。
题 2:已知正方体 ABCD-A1B1C1D1,如图 7,F点为体对角线BD1的四分之一分点,靠近B,求过点A,C,F的平面与棱BB1的交点。
题 3:已知正方体 ABCD-A1B1C1D1,如图 8,F点为体对角线BD1的四分之一分点,靠近B,求过点D,C,F的平面与棱BB1的交点。
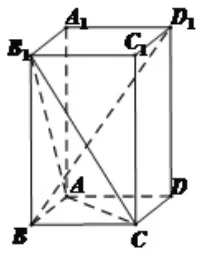
图(6)
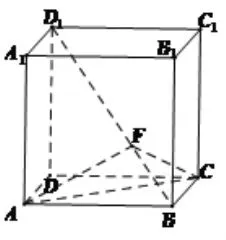
图(7)
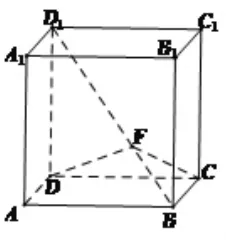
图(8)
显然,对于这三个例子,方法一与方法二不适合,应当用方法三。题1的解答与方法三完全一样,不再赘述。题2作法:连接BD交AC于点M,连接MF并延长交BB1于点H,H为所求交点。
题3作法:连接DF并延长交BB1于点N,点N为所求交点。
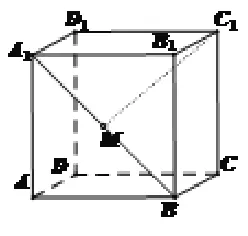
图(9)
还可以拓展一些直线与平面交点在几何体外的类型题。
题4:已知正方体 ABCD-A1B1C1D1,如图 9,点M为A1B的中点,求C1M与平面ADD1A1的交点.
完成练习之后,再次让学生总结,三个公理的作用是什么,交点可以通过什么来求。
必修2教材的习题B组中,有对公理应用的配备练习,即三点共线和三线共点问题,应当有效地利用起来。在教学中,强调公理的作用能培养学生的理性思维和应用公理定理解决问题的能力。
四、强化几何作图教学,提升空间想象能力
在初等教育中,几何是一门很形象的学科,是研究图形的大小和位置关系。学生一开始很容易就喜欢上几何,因为图形来源于直观的生活,却在最后很容易就放弃几何,因为无法把图形还原于直观的生活。所以,在立体几何教学中,我们对任何抽象小题研究的目的都思考:如何培养学生的空间想象能力。
通过这个简单试题,发现在多个解题方法中,最简单的也最容易被忽视的方法是应用公理的方法三,即几何作图能力。简单的平面几何作图,对高中生来说已经很简单,但是立体几何图形的作图就有难度了。
教学的第一步,如教材中用斜二侧画法来画一个整体的立体图形,如长方体、直六棱柱。先画底面,再画侧棱,最后将上底面各个顶点顺次链接起来。这种画法让学生可以很快感受到一个几何体的直观图。但是对于几何体内部点、线、面的关系就需要进一步的引导。需要引导学生先找到点的位置,进而找到线的位置,有了线的位置,就能找到面的位置。
公理是立体几何的基石,是所有定理和重要结论存在的依据,是将对点、线、面的直观感知转化成准确位置关系的重要依据。课标中指出:公理对学生建立空间感,实现从认识平面几何到认识空间几何具有十分重要的促进作用。考纲中要求“能运用公理、定理和已获得的结论证明一些空间图形位置关系的简单命题”,所以要重视培养学生使用公理看待问题的意识和能力。
过去的考试中,对立体几何公理的考察基本只出现在文字判断辨析中,而作图既能考察学生的空间推理证明能力,又能考查学生将知识应用于生活的实践能力。近几年高考题,立体几何作图找点等问题回到了人们的视线中,这提示我们不能忽略公理使用的教学,要培养学生的空间想象能力与应用意识。
G632
A
1671-6531(2017)09-0074-03
田炜歌/长春市第七中学二级教师(吉林长春130051)。
责任编辑:苏 航
