铜管爆破压力计算公式

杨 帆 刘 岑 刘 兵 吴元祥 范有雄 刘小宁

(1.武汉软件工程职业学院 机械工程学院 湖北 武汉：430205； 2.湖北轻工职业技术学院 机电工程学院 湖北 武汉：430070)

铜管爆破压力计算公式

杨 帆1刘 岑2刘 兵1吴元祥1范有雄1刘小宁1

(1.武汉软件工程职业学院 机械工程学院 湖北 武汉：430205； 2.湖北轻工职业技术学院 机电工程学院 湖北 武汉：430070)

为准确计算铜管的爆破压力，应用概率论与数理统计知识，建立了评价铜管爆破压力计算公式精度的随机变量。基于TP2铜管的12组爆破试验数据，对计算其爆破压力的3个公式进行了比较与分析。研究表明，在双侧置信度为99%时，用中径公式计算铜管的爆破压力，该随机变量的均值不小于0.861且不大于1.071，标准差不小于0.072且不大于0.230，变异系数不小于0.068且不大于0.267。与其他计算两个公式相比，中径公式精度高，可用于计算铜管最大工作压力与最大水压试验压力。

铜管；爆破压力；中径公式；精度

在卫生医疗、食品医药领域以及空调制冷系统中，经常采用铜管输送有一定工作压力的液体或者气体，为确保安全，我国采用有关标准规范铜管的设计与试验[1,2]。

准确计算铜管爆破压力，是涉及铜管安全使用的基础工作。根据标准[1]提出的最大工作压力计算公式，以及标准[2]提出的最大水压试验压力计算公式，推导得到的铜管爆破压力表达式不同。长期工程实践证明，钢制薄壁压力容器爆破压力可用中经公式计算[3]，但其是否能用于计算铜管爆破压力值得探究。由于精度是指公式计算值与实测值的接近程度，因此选择精度高的公式，统一计算铜管爆破压力、最大工作压力与最大水压试验压力是值得研究的课题。

文中应用概率论知识，建立了评价铜管爆破压力计算公式精度的随机变量，基于材质为软态TP2的铜管12组爆破试验数据，对3个爆破压力计算公式的精度进行了比较与分析。

1 基本理论与方法

1.1 计算爆破压力的不同公式

根据标准[1]提出的最大工作压力计算公式，可推导得到铜管爆破压力表达式：

(1)

式中，ub1为铜管爆破压力的第1个公式计算值，MPa；t为铜管壁厚(光管)或者底壁厚(内螺纹管)，mm；Rm为铜管材质的抗拉强度，MPa；D为铜管外直径，mm。

根据标准[2]提出的最大水压试验压力计算公式，可推导得到铜管爆破压力表达式：

(2)

式中，ub2为铜管爆破压力的第2个公式计算值，MPa。

假设铜管爆破压力可用中径公式[3]计算：

(3)

式中，ub3为铜管爆破压力的第3个公式计算值，MPa。

1.2 基本理论

1.2.1 建立评价计算公式精度的随机变量ri

假设铜管爆破压力Pb是随机变量，ubi是第i个爆破压力计算公式的计算值，其中i=1，2，3；显然，评价ubi精度的随机变量ri为：

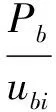
(4)

通过爆破试验，可获得铜管爆破压力的p个样本数据Pbj(j=1，2，…，p)，ri的统计量为：

(5)

式中，Pbj为爆破压力的第j个实测值，MPa；ubi,j为用第i个公式计算得到爆破压力的第j个值，MPa。

ri样本的平均值与精密度分别为[4,5]：

(6)

(7)

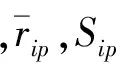
1.2.2 ri分布参数

双侧置信度为(1-α)时，ri均值μri的取值区间为[4,5]：

μri∈[μrimin，μrimax]

(8)

其中

(9)

(10)

式中，μrimin与μrimax分别为均值μri在双侧置信度为(1-α)时的下限与上限。

双侧置信度中的α，是指将满足式(8)的μri，误判为μri<μrimin或μri>μrimax的风险概率各为0.5α。工程上一般取α=0.01[6]，文中所用t分布系数见表1[4,5]。

表1 t系数

双侧置信度为(1-α)时，ri标准差σri取值区间为[4,5]：

σri∈[σrimin，σrimax]

(11)

其中

(12)

(13)

式中，σrimin与σrimax分别为标准差σri在双侧置信度为(1-α)时的下限与上限。

此处双侧置信度中的α，是指将满足式(11)的σri，误判为σri<σrimin或σri>σrimax的风险概率各为0.5α。

表22系数

变异系数是标准差与均值之比，当双侧置信度为(1-α)时，ri变异系数Cri取值区间由式(5)与式(8)可得：

Cri∈[Crimin，Crimax]

(14)

其中

Crimin=σrimin/μrimax，Crimax=σrimax/μrimin

(15)

式中，Crimin与Crimax分别为变异系数在双侧置信度为(1-α)时的下限与上限。

此处双侧置信度中的α，是指将满足式(14)的Cri，误判为CriCrimax的风险概率各为0.5α。

1.3 比较与分析

可从随机变量ri的准确性与集中性两个方面，对铜管爆破压力计算公式(i)的精度进行比较与分析。

1.3.1 准确性

随机变量ri的均值μri是式(i)准确性的量度。μri>1表明公式计算值小于试验值偏于安全，μri<1表明公式计算值大于试验值偏于危险，μri=1说明公式计算值能准确反映试验值，这是理想状态。

从概率论角度，μri应是通过对所有相同的铜管进行爆破试验以后得到的确定值，由于爆破试验是破坏性试验，从工程实际的角度而言，得到μri的确定值是不可能的，但是从数理统计知识可知，通过部分相同铜管(样本)的爆破试验，可得到ri样本的平均值与精密度，从而确定μri的范围即取值区间，见式(8)。

为了保证铜管爆破压力计算公式(i)的准确性高，μri的取值区间即式(8)中必须包括“1”，并且波动范围μrimax-μrimin必须小，即μri的稳定性要好。

1.3.2 集中性

随机变量ri的标准差σri与变异系数Cri是式(i) 集中性的量度。从工程实际的角度，通过部分相同铜管的爆破试验，可得到ri样本的平均值与精密度，从而确定标准差σri与变异系数Cri的范围即取值区间，见式(11)与式(14)；由式(6)与式(7)，式(11)与式(14)可知，标准差σri与变异系数Cri是不为零的正数，标准差σri与变异系数Cri小，表明试验数据集中在一起，爆破压力计算公式(i)的集中性好；σri与Cri大，表明试验数据分散，爆破压力计算公式(i)的集中性差。研究表明，变异系数Cri比标准差σri相对更加重要[7]。

为了保证铜管爆破压力计算公式(i)的集中性好，①σri的取值区间即式(11)中的σrimax必须小，并且波动范围即σrimax-σrimin必须小，即σri的稳定性要好。②Cri的取值区间即式(14)中的Crimax必须小，并且波动范围Crimax-Crimin必须小，即Cri稳定性要好。

2 爆破压力试验数据及统计

有关企业利用材质为软态TP2的直铜管进行室温液体爆破试验，获得12了组试验数据(见①http://gc.100 xuexi.com/ExamItem/ExamDataInfo.aspx?id=39434A0D-8843-4D03-A200-D528B46B04FA铜管和热交换器的耐压性和爆破压力，②https://wenku.baidu.com/view/ d640dc5a0740be1e650e9a9f.html铜管爆破实验报告)，软态TP2铜管的室温抗拉强度Rm为205MPa；现将爆破试验数据与有关公式ri的统计值一并列入表3中。

表3序号9～12的直铜管爆破口出现在钎焊处，其中10与11号爆破压力比较低，表明钎焊加热可使焊缝附近的铜管被退火，严重时会产生过热和过烧，导致铜管爆破压力降低[14]，这种现象应引起足够重视。

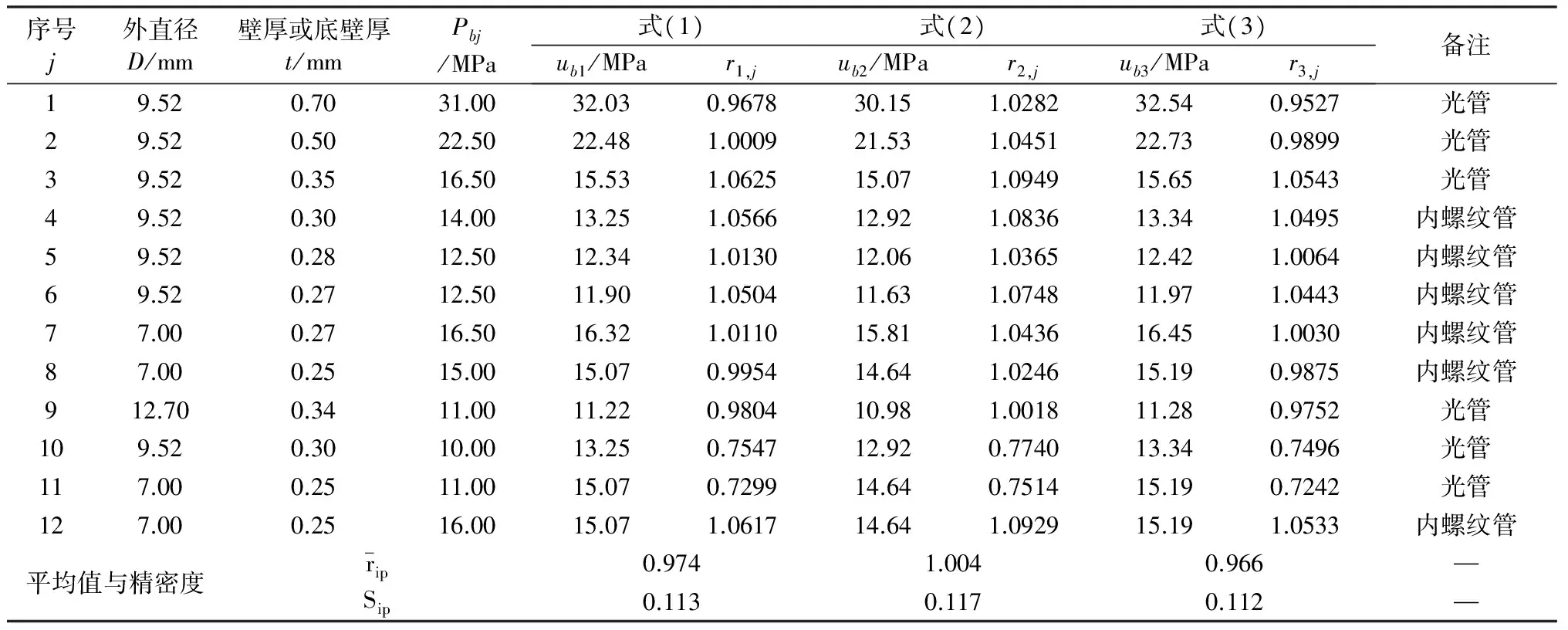
表3 铜管爆破试验数据及统计

3 公式精度的比较与分析

在分布参数的双侧置信度为99%时，将表3中平均值与精密度代入式(8)～式(15)中，可得到ri分布参数的取值区间，见表4。

将评价式(1)、式(2)与式(3)精度的随机变量ri，从均值μri、标准差σri与变异系数Cri三个指标进行比较与分析，一并列入表4。

由表4可知，用中径公式(3)计算铜管爆破压力，评价其精度的随机变量r3的均值μr3、标准差σr3与变异系数Cr3波动范围小，稳定性好，公式准确性高与集中性好，具有精度高的特点；建议有关标准[1,2]统一采用中径公式，提高计算铜管最大工作压力与最大水压试验压力的精度。

表4 三个公式的比较与分析

4 讨论

某企业为美国制造一批热交换器，要求U形铜制换热管在压力为14.5MPa时，保持30秒不泄漏不爆破。该企业采用材质为软态TP2的内螺纹铜管制作U形换热管，尺寸为：外直径D为9.52mm，底壁厚t为0.30mm，螺纹齿高为0.20mm；并模拟热交换器工作状态，在安装铝翅片后进行水压爆破试验，为提高U形换热管爆破压力，超压处理压力分级提高，每级压力保持30秒，最后一次降压为0再升压直至爆破。

铜管爆破前的部分超压处理压力数据(见http://gc.100xuexi.com/ExamItem/ExamDataInfo.aspx?id=39434A0D-8843-4D03-A200-D528B46B04FA铜管和热交换器的耐压性和爆破压力)、爆破压力的实测值Pbj、中径公式(3)计算值ub3及统计量r3,j均列入表5。

由于软态TP2铜材的屈服强度只有抗拉强度的三分之一左右[15]，根据中径公式(3)，铜管的屈服压力也只有爆破压力的三分之一左右；由表4可知：未经过加工的，外直径D为9.52mm且底壁厚t或者壁厚t为0.30mm软态TP2铜管，其爆破压力实测值在10.00MPa～14.00MPa，对应的屈服压力只有3.33MPa～4.67MPa；而由表5可知：对铜管预处理压力超过屈服压力时，尽管其壁厚有所减薄，但是铜管爆破压力仍然提高到16.70MPa～17.40MPa，比中径公式的计算值增加25.2%以上，比未经过加工铜管的爆破压力高2.70MPa～7.40MPa；笔者认为，这主要是铜管的超压处理引起TP2铜材的冷作硬化，导致其抗拉强度上升的结果。

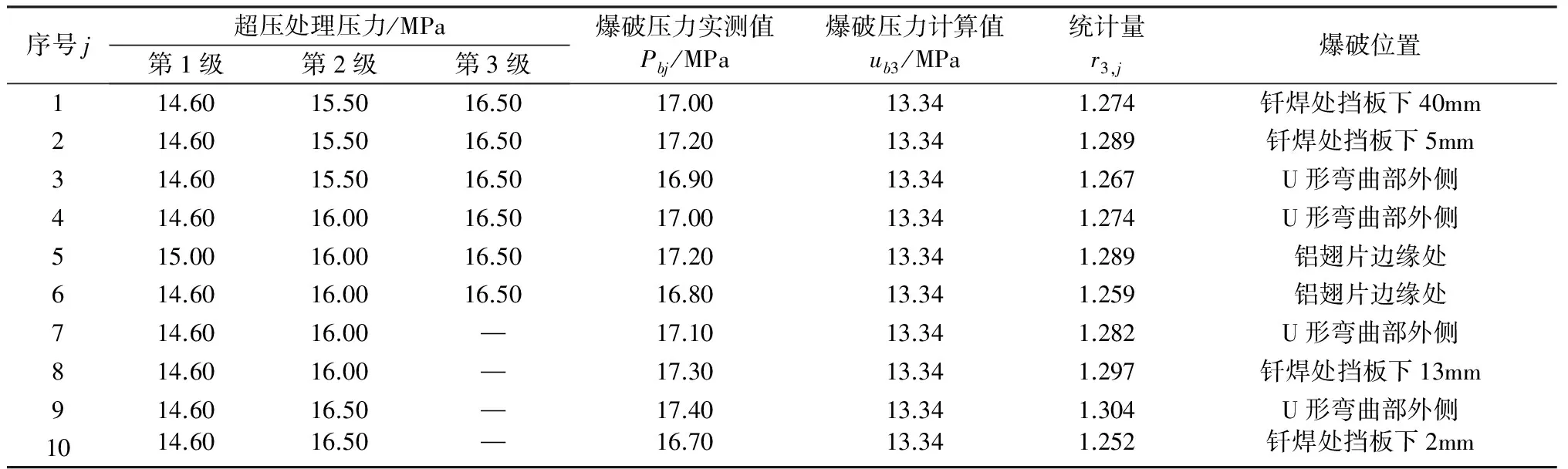
表5 超压处理软态TP2内螺纹铜管爆破压力的实测值与计算值对比

表3序号为10、11的直铜管受钎焊过热和过烧的影响，导致铜管爆破压力降低；从表5序号为1、2、8与10的试验来看，尽管铜管爆破位置在钎焊热影响区，但在超压处理后，铜管爆破压力仍然得到显著提高，表明超压处理可提高TP2铜材在钎焊热影响区的抗拉强度。表5序号为6、7的铜管爆破位置在铝翅片边缘处，表明铝翅片对铜管爆破压力有一定提高效果[16-18]；由于U形弯曲部外侧是壁厚减薄严重之处，因此，表5序号为3、4、7与9的铜管在该处爆破。

根据以上分析，软态TP2铜管进行合适的超压处理，似为提高其爆破压力有效方法之一，其产生的机理值得进一步研究。

5 结论

(1)应用概率论与数理统计知识，建立了评价铜管爆破压力计算公式精度的随机变量。基于软态TP2铜管的12组爆破试验数据，对有关标准采用的3个爆破压力计算公式的精度进行了比较与分析。

(2)用中径公式计算铜管的爆破压力，在双侧置信度为99%时，评价公式精度随机变量的准确度不小于0.861且不大于1.071，标准差不小于0.072且不大于0.230，变异系数不小于0.068且不大于0.267。

(3)与其他两个计算公式相比，用中径公式计算铜管的爆破压力，具有准确性高与集中性好的特点；建议有关标准统一采用中径公式，提高计算铜管最大工作压力与最大水压试验压力的精度。

(4)软态TP2铜管进行超过屈服压力的处理，似为提高铜管爆破压力有效方法之一，其产生的机理值得进一步研究。

[1] GB/T 108833—2007,无缝铜水管与铜气管[S].

[2] GB/T 241—2007,金属管液压试验方法[S].

[3] GB 150.1～150.4—2011,钢制压力容器[S].

[4] 熊德之,张志军.概率论与数理统计及其应用[M].北京:科学出版社,2007:131-262.

[5] 化学工程手册编辑委员会.化工应用数学[M].北京:化学工业出版社,1983:23-28,369-375.

[6] 徐灏.机械强度的可靠性设计[M].北京:机械工业出版社,1984:1-220.

[7] 刘小宁,刘岑,张红卫,等.对“基于实测数据的特种球形压力容器爆破压力计算公式”一文的商榷[J].应用数学和力学,2016,37(5):552-550.

[8] 李清,袁小会,刘岑,等.有效试验数据对钢材机械性能分布规律的影响[J].武汉工程大学学报,2015,37(4):69-73.

[9] 刘岑,杨帆,吴元祥,等.钢材拉伸试验数据同质性的判别[J].武汉工程职业技术学院学报,2017,29(2):17-19.

[10] 刘岑,袁小会,刘兵,等.钢制单层球形容器爆破压力的计算[J].武汉工程大学学报,2016,38(3):299-306.

[11] 刘小宁,刘岑,吴元祥,等.超高压圆筒容器爆破压力计算公式的比较[J].机械强度,2015,37(2):373-376.

[12] 杨帆,刘岑,刘兵,等.钢制薄壁容器爆破压力计算公式评价[J].现代制造工程,2016,(11):124-128.

[13] 刘小宁,刘岑,刘兵,等.单层厚壁内压圆筒设计公式改进效果的可靠性研究[J].机械强度,2016,38(2):276-283.

[14] 戴佶,陆皓,陈俊梅.考虑温度履历的铜管钎焊接头爆破压力研究[J].焊接,2012,(2):22-25.

[15] 戴佶.基于温度履历的铜管钎焊接头爆破压力研究[D].上海:上海交通大学,2010.

[16] 张红卫,刘岑,陈刚,等.确定短ABS塑料圆管爆破压力的经验公式[J].化肥设计,2010,48(5):18-19.

[17] 刘小宁,张红卫,刘岑,等.钢制薄壁内压短圆筒静强度的试验研究[J].压力容器,2009,26(7):11-14.

[18] 杨帆,刘岑,叶志娟,等.U肋内焊技术的工艺参数优化研究[J].武汉工程职业技术学院学报,2017,29(1):15-17.

CopperTubeBurstPressureCalculationFormula

Yang Fan1Liu Cen2Liu Bing1Wu Yuanxiang1Fan Youxiong1Liu Xiaoning1

(1.School of Mechanical Engineering, Wuhan Vocational College of Software and Engineering, Wuhan 430205, Hubei; 2.School of Mechanical and Electrical Engineering, Hubei Light Industry Technology Institute, Wuhan 430070, Hubei)

To accurately calculate copper tube burst pressure, by applying probability theory and mathematical statistics, using random variables to evaluate precision of copper tube burst pressure, calculation formula were established. Based on the 12 groups of burst test data of TP2 copper tube, three calculation formulas of the copper tube burst pressure were compared and analyzed. Studies have shown that: when bilateral confidence level reaches 99%, using the mid-diameter formula to calculate the copper tube burst pressure, the random variable mean should be between 0.861 and 1.071, the standard deviation should be between 0.072 and 0.230, and the variation coefficient should be between 0.068 and 0.267. Compared with other two calculation formulas, the precision of mid-diameter formula is better in precision. For copper tube with maximum working pressure and the maximum hydraulic test pressure, the mid-diameter formula could be adopted.

copper tube; burst pressure; mid-diameter formula; precision

TG146.1+；TH121

A

1671-3524(2017)03-0012-05

2017-08-01

2017-08-29

湖北省教育厅科研项目(B2016545)；武汉市黄鹤英才(教育)计划

杨 帆(1989～)，男，硕士，助理工程师.E-mail：15172540623@163.com

(责任编辑：李文英)