等离子喷涂热障涂层拉伸过程中的裂纹扩展有限元模拟

邵洪旭

(武汉工程职业技术学院 湖北 武汉：430080)

等离子喷涂热障涂层拉伸过程中的裂纹扩展有限元模拟

邵洪旭

(武汉工程职业技术学院 湖北 武汉：430080)

基于等离子喷涂涂层显微组织图片构建有限元模型，准确反映孔洞、裂纹等缺陷在涂层中的实际分布特征。利用LS-DYNA有限元方法计算拉伸过程中涂层内部的应力变化，以最大主应力作为涂层材料的失效判据，模拟裂纹萌生、扩展过程。数值模拟结果表明，喷涂过程中在陶瓷层内形成的横向主裂纹尖端是拉伸过程中裂纹扩展的萌生点，裂纹在扩展过程中与原有缺陷相互作用使得扩展的裂纹发生了分叉以及偏转，真实再现了裂纹扩展引起涂层失效的过程。

热障涂层；有限元模拟；裂纹扩展；断裂拉伸

等离子喷涂热障涂层体系(plasma-sprayed thermal barrier coatings, PS TBCs)一般包括基体、金属粘结层(BC)、陶瓷隔热层(TC)等[1]。涂层结合强度包括涂层与基体之间的粘结强度以及涂层自身的内聚强度，是反映涂层性能高低的一个重要指标,若结合强度过小，将造成涂层局部起皮、剥落，导致涂层服役寿命降低[2]。涂层结合强度通常采用轴向拉伸法来测定，与涂层拉伸失效相关的主要因素包括：(1)外加拉伸载荷的强度；(2)涂层材料自身的本征力学性能；(3)涂层在等离子喷涂制备过程中形成的孔洞、裂纹等缺陷及其分布；(4)涂层内不同材料之间的层间界面等[3-6]。由于这些因素综合作用，使得对涂层在承受拉伸载荷作用时的裂纹扩展过程研究显得尤为困难。

本文以等离子喷涂热障涂层为研究对象，利用自主开发的基于涂层图片有限元模型生成程序，建立能真实反映涂层中孔洞、裂纹等缺陷分布的有限元模型，进一步进行涂层拉伸过程中的裂纹扩展模拟。

1 实验方法

采用薄膜粘接轴向拉伸法进行涂层拉伸试验测试。陶瓷层厚度为350μm，试样尺寸设计为φ25mm×10mm，选用FM1000薄膜胶作为粘结剂。将制备好的拉伸试件装卡在电子式万能试验机上，采用1mm/min的速率加载，直至涂层内部发生分离或从基体上剥离。通过对涂层试样拉伸失效断口形貌观察发现失效主要发生在陶瓷层内部靠近粘结层的位置。

2 计算方法

本文开发了一种基于涂层真实的显微组织图片构建有限元模型，模拟拉伸引起的应力变化以及裂纹扩展直至失效的整个过程。热障涂层拉伸失效更容易在陶瓷层内发生的主要原因是：(1)粘结层具有较好的延展性，室温下其屈服应力可以达到426MPa[7]，而陶瓷层为脆性材料，断裂发生较为容易；(2)陶瓷层中含有一定数量的孔洞、裂纹等缺陷，涂层在拉伸过程中应力极易在这些缺陷的尖端迅速累积，导致断裂失效。

2.1 有限元模型

轴向拉伸过程中，应力主要沿着喷涂方向从端面向涂层内部传递，涂层中的缺陷分布对应力的传递以及裂纹扩展都将产生重要的影响；同时，拉伸失效的位置主要是在界面附近的陶瓷层。基于上述特点，在选取用于拉伸模拟的涂层显微组织图片中应关注以下两点：(1)含有TC/BC的界面形貌特征；(2)所建几何模型中，陶瓷层应选取足够的厚度以充分反映裂纹的扩展路径[8]。

选用放大倍数为350倍的涂层显微组织扫描电镜(SEM)图片为有限元建模对象，如图1所示，陶瓷层的厚度在200μm左右，能够充分反映裂纹的扩展路径；同时，TC/BC的界面形貌特征也能很好的展现出来。采用自主开发的基于材料显微组织图片的有限元模型生成方法(具体方法见文献[8-12])，基于图1建立如图2所示的有限元网格模型，其网格单元数约为62500，为有限元计算提供了较好的网格精度。

图1 横截面显微组织图片

图2 有限元网格模型

2.2 材料模型及载荷

陶瓷层(TC)材料选用弹性材料模型，粘结层(BC)材料选用弹塑性材料模型。轴向拉伸过程中，TC失效主要表现为拉应力引起的裂纹扩展，因此本文采用最大主应力作为TC材料的失效判据，采用中间钻孔巴西圆盘试验测得TC材料YSZ的失效判据为215MPa[13]，用于计算的具体材料参数如表1[13]所示。

表1 材料性能参数[13]

选择模型的上下两端面为载荷施加对象，固定一端面，在另一端面施加随时间变化线性增加的应力载荷，加载速率为1MPa/s。

3 计算结果

采用LS-DYNA有限元软件模拟拉伸过程中涂层裂纹扩展直至失效的过程，把试验中无法观察到的失效过程真实地再现出来。图3和图4是两张典型的涂层横截面微区SEM图片，其显微组织特征分别是喷涂过程中在TC/BC界面以及陶瓷层内接近TC/BC界面处形成了较长的裂纹，涂层在拉伸过程中的失效易于从这些缺陷处发生。

图3 TC/BC界面附近含有较长裂纹

图4 陶瓷层内含有较长裂纹

图5至图12分别为图3和图4在不同时刻的裂纹扩展有限元模拟图。

图5和图6给出了载荷增加至一定程度时的应力变化情况。从图5及图6中可以看出，A区域和B区域为应力峰值所在区域，当载荷施加时间为35.2s时，A区域的应力峰值已经达到202MPa；B区域的应力峰值在载荷施加至31s时为208MPa。当外加载荷继续增加时，裂纹将优先在A区域的界面附近或者B区域的陶瓷层内形核，反映出两种典型的裂纹形核位置。

图5 35.2s时受载界面附近裂纹性有限元模拟图

图6 31s时受载陶瓷层内裂纹有限元模拟图

图7给出了加载时间为35.3s时图3的裂纹扩展模拟图。从图7中可以看出，裂纹沿TC/BC界面向左右两方向扩展，受到TC/BC界面附近处缺陷的影响，当裂纹扩展到缺陷附近时，将发生偏转，向陶瓷层内扩展；图8给出了加载时间为31.1s时图4的裂纹扩展模拟图。从图8中可以看出，在陶瓷层内原有缺陷处裂纹开始扩展。

图7 35.3s时界面附近裂纹扩展模拟图

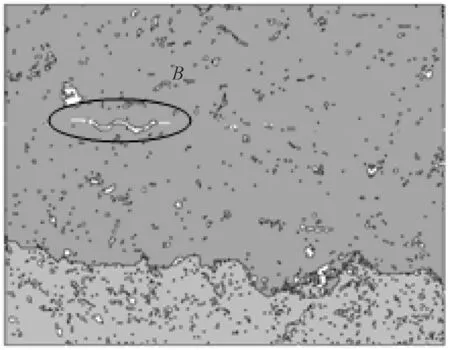
图8 31.1s时陶瓷层内裂纹扩展模拟图

随着外加载荷的持续增加，裂纹继续扩展。当加载时间为35.6s时，从图9中可以观察到，图3的裂纹在向右侧方向横向扩展的过程中经过陶瓷层内的微孔洞时，会在原有缺陷处形成次生裂纹，表现为横向扩展的主裂纹发生了细小的分叉；同时，由于剪切作用，在涂层微区上端面原有缺陷处最大主应力迅速增加，裂纹开始萌生并沿斜向下方向扩展。图10给出了加载时间为31.4s时图4的裂纹扩展模拟图。从图10中可以看出，裂纹在向左侧方向扩展的同时也向右侧方向开始扩展，并很快贯穿至模型的左侧边界。

图9 35.6s时界面附近裂纹扩展模拟图

图10 31.4s时陶瓷层内裂纹扩展模拟图

图11给出了加载时间为36s时图3被完全拉断的模拟图。从图11中可以看出，图3被拉断的过程中，在除了横向扩展的主裂纹之外的其它地方也出现了次生裂纹，主要是因为在主裂纹横向扩展的过程中，图3中其它较大缺陷周围的应力值也达到了失效应力值，次生裂纹开始扩展。同时，斜向下扩展的裂纹由于缺陷的作用，改变了原有的扩展路径，不断发生分叉；加载时间为31.6s时，图4被完全拉断，如图12所示。从图12中可以看出主裂纹横向扩展过程中经过陶瓷层内的缺陷时，横向扩展的主裂纹发生了一定程度的分叉偏转。尽管图中存在两种不同的形核位置(界面处形核、陶瓷层内形核)，但最终都是在陶瓷层内靠近界面位置附近形成主裂纹直至贯穿型断裂，这与试验观察到的现象相吻合，反映了模拟方法的准确性，为进一步的涂层拉伸结合强度预测提供了可靠的方法。

图11 36s界面附近裂纹扩展模拟图

图12 31.6s时陶瓷层内裂纹扩展模拟图

4 结论

(1)采用自主开发的基于材料显微组织图片的有限元模型生成方法，建立能反映孔洞、裂纹等缺陷真实分布的有限元模型；

(2)利用LS-DYNA有限元方法，模拟在拉伸过程中涂层微区内的应力变化，模拟结果表明陶瓷层内的横向主裂纹为应力峰值集中区域，是裂纹扩展的萌生位置；

(3)尽管存在两种不同的典型形核位置(界面处形核、陶瓷层内形核)，但最终都是在陶瓷层内靠近界面位置附近形成主裂纹直至贯穿型断裂。裂纹扩展过程中与原有缺陷相互作用使得扩展的裂纹发生了分叉以及偏转，改变了裂纹的扩展路径；

(4)拉伸过程中的裂纹扩展模拟能很好地反映涂层的失效过程，为进一步的涂层拉伸结合强度预测提供了可靠的方法。

[1] Padture N P, Gell M, Jordan E H. Thermal Barrier Coatings for Gas-Turbine Engine Applications[J]. Science.2002,296(5566):280-284.

[2] 王全胜.纳米氧化锆热防护涂层微结构控制及热冲刷失效机理研究[D].北京：北京理工大学,2009.

[3] Andritschky M, Teixeira V, Rebouta L, et al. Adherence of combined physically vapour-deposited and plasma-sprayed ceramic coatings[J]. Surface and Coatings Technology,1995,76-77(Part 1):101-105.

[4] Gell M, Eric J, Krishnakumar V, et al. Bond strength, bond stress and spallation mechanisms of thermal barrier coatings[J]. Surface and Coatings Technology,1999,120-121:53-60.

[5] Cao N Y, Kagawa Y, Liu Y F. Stress analysis of a barb test for thermal barrier coatings[J]. Surface and Coatings Technology,2008,202(14):3413-3418.

[6] Cao N Y, Liu Y F, Kagawa Y. Finite element analysis of a barb test for thermal barrier coating delamination toughness measurement[J]. Surface and Coatings Technology,2008,202(13):3109-3114.

[7] Busso E P, Wright L, Evans H E, et al. A physics-based life prediction methodology for thermal barrier coating systems[J]. Acta Materialia,2007,55(5):1491-1503.

[8] 沈伟.基于等离子喷涂热障涂层的性能模拟理论与方法研究[D].北京：北京理工大学,2011.

[9] Shen Wei, Wang Fu-chi, Fan Qun-bo, Hua Dan, Ma Zhuang. Proposal of new expressions for effects of splat interfaces and defects on effective properties of thermal barrier coatings[J]. Surface&Coating Technology,2010,204:3376-3381.

[10] Shen Wei, Fan Qun-bo, Wang Fu-chi, Ma Zhuang. Modeling of micro-crack growth during thermal shock based on microstructural images of thermal barrier coatings[J]. Computational Materials Science,2009,46:600-602.

[11] 沈伟，范群波，王富耻，马壮，杨学文.基于数字图像处理技术的等离子喷涂氧化锆涂层热导率影响因素有限元方法研究[J].无机材料学报，2010，25：1217-1220.

[12] 沈伟，范群波，王富耻，马壮.基于显微组织图片的涂层热导率有限元计算研究[J].人工晶体学报，2009，38：267-270.

[13] Shen Wei, Wang Fu-chi, Fan Qun-bo, Ma Zhuang, Yang Xue-wen. Finite element simulation of tensile bond strength of atmospheric plasma spraying thermal barrier coatings[J]. Surface & Coating Technology.2011,205:2964-2969.

FiniteElementSimulationofMicro-cracksGrowthofPlasmaSprayedCoatingsduringTensileprocessing

Shao Hongxu

(Wuhan Engineering Institute, Wuhan 430080, Hubei)

Based on microstructures of plasma sprayed coatings, finite element models are built to reflect actual distribution of pores and micro-cracks in coatings. LS-DYNA finite element method is employed to model the stress changing when suffering tensile processing, with a failure criterion determined by the maximum principal stress, and the micro-cracks growth is simulated. The numerical simulation results show that the major transverse crack generate during plasma spraying have the largest stress intensity factor, which is exactly the crack propagation location. It is found that the growth cracks will bifurcate and deflect when interacting with the original defects, reflecting the coatings’ failure process.

plasma sprayed coatings; finite element method; micro-cracks growth; tensile fracture

TP319

A

1671-3524(2017)03-0028-04

2017-08-10

2017-08-25

邵洪旭(1982～)，男，大学，讲师.E-mail:46574268@qq.com

(责任编辑：李文英)