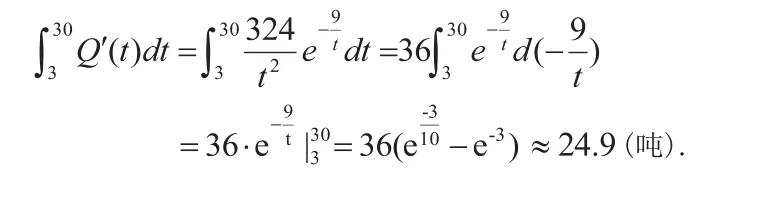积分在工程投资回报中的应用

贺胜平

重庆商务职业学院

积分在工程投资回报中的应用

贺胜平

重庆商务职业学院

积分在经济生活以及实际问题中有广泛的应用，而数学建模又是把实际问题化为数学命题来解决.本文着重通过数学建模的方式，结合定积分的计算和微分方程的相关内容介绍其在工程投资回报中的应用.

积分；工程投资回报；应用

当大家在开拓某一项目时，投资回报题目总要思量的，即在必然的时期内与一定的收益率要预期到达某一目标，必需投入一定的现值；或在一定的收益率下，投入一定的现值，要达到某预期的目标，项目的投资回收期等问题。

由于定积分可计算在某一范围内，已知变化率求总量以及增量的问题。所以下面我们先通过数学建模的方式解决工程投资回报的题目。

一、数学建模解决

为了便于对投资项目有一个领会，我们可通过创设数学模型，对这一动态经济题目加以分析.

1.模型假设

(1)假设项目作持续复利计算，且资金的年利率r相对稳定；

(2)若设此项目的收益率在t(年)时是f (t)(万元)，那么该贴现率就是f (t)e-rt；

(3)项目在投资过程中我们暂时不思量其他滋扰的成分.

2.模型建立

该项目在时间[0, T ]内的总收益是

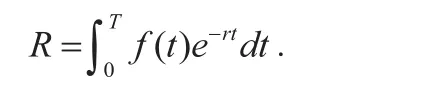
3.模型求解

若是收益率f (t)=A(A是常数)，称此时是平均收益率，那么总收益的现值是

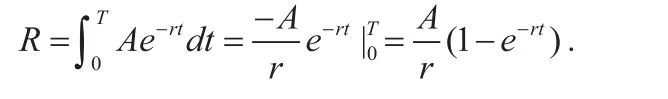
假设期初的投资额是a，那么此投资的纯收益贴现值是

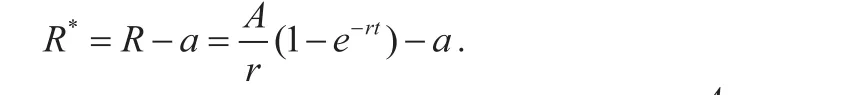
4.模型应用

(1)假设连续3年的年贴现率是5%，且收益率固定保持在200(万元/年)，那么它的现值又几何？

由公式得

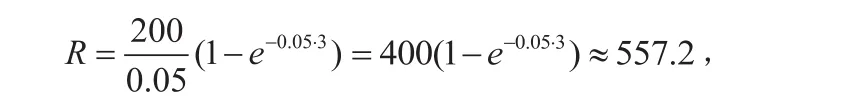
其现值是557.2万元.

(2)如果此项工程投资800万元，年利率为5%，且10年内的均匀收益率是200(万元/年)，求投资回收期与投资所得的纯收益分别是多少？

由公式得

因而投资所得纯收益是

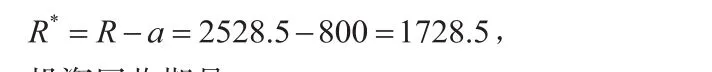
投资回收期是

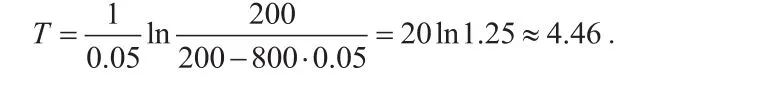
所以可得，在10年中该投资可得的纯利润为1728.5万元，4.46年即为投资回收期.

二、积分计算解决

对于下列残值、增量以及总量等涉及经济问题，我们还可直接通过积分计算来解决.

案例1、要是某一条小河已被污染得比较严重，且现拥有V(单位：km3)库存量.经测量，现在的污染物总量已到Q0(单位：吨)，且污染物平均地分部在水里.假设现已不再向小河排污，净水以不变的速率r (单位：km3/年)流入小河，并立即和小河的水相混合，小河的水也以相同的速率r流出.如果起初的时刻是t=0.

(1)求当在时刻t时，小河中残留污染物的数量Q(t).

(2)若要使小河中污染物的数目回到起初的10%，还得经过几年.

解 (1)由题意可得，当时间t(t ≥ 0)，Q(t)的变化率＝－(污染物的流出速率).

分离变量得

案例2、设某产品是连续生产的，总产量Q是时间t的函数.如果总产量的变化率是(单位：吨/日)，问投入生产后由t=3到t=30此27天的总产量是多少？

解 总产量Q(t)是其变化率Q′(t)的原函数，所以从t=3到t=30这27天的总产量是