从“有法”到“无形”

■龚 震

从“有法”到“无形”

■龚 震

大学毕业，笔者和众多青年教师一样，带着对神圣职业的热爱和些许空乏的心理学、教育学理论走上讲台，但却发现无从下手。与许多年轻教师不同的是，笔者幸运地师从全国著名特级教师李庾南，在她所创立的“自学·议论·引导”教学法的引领下，一路走来，教师专业成长的道路变得顺畅而宽广。

一、从模仿到理解

始入课堂，如同一张白纸，能够随时听到像师傅这样的特级大师的随堂课是多么幸福，总被李老师那自然流畅的教风教态、科学严谨而又不失温和的教学语言、游刃有余的教学技巧所折服。为什么李老师的课总能让听者都陶醉在其中？为什么她问的问题都能引起学生积极的思维共鸣？她与同学们的交流问答为什么会那么流畅自然呢？当时我们不明白其中的教学原理，只是觉得这就是好课。我们几个年轻人开始模仿，模仿她的每一句话、每一个动作、每一丝微笑，幻想着有一天能够将这样的课搬入自己的课堂！然而事与愿违，为什么李老师那么热情洋溢、充满着智慧与感染力的语言在我们嘴里背出来显得那么干涩无力、不知所云？为什么李老师与学生酣畅淋漓、积极踊跃的交流到了我们课上就变得磕磕绊绊、冷冷清清？一堂课我们能做到的只是该讲几个知识点，要讲哪些例题。带着这样的疑惑去请教师傅，李老师微笑着拿出两本介绍“自学·议论·引导”教学法思路的书说道：“你们只知道听我在讲什么，但你却不知道我为什么要这样去设计，我这样做要达到什么样的教学目标，为了达到这些目标，我又采用了哪些方式，设计了哪些环节。这些书里介绍了我的教学方法和理念，多看看自然会明白的。”

如获至宝，仔细研读。慢慢地读懂了李老师每堂课的精彩，悟出了“自学·议论·引导”教学法的一些“妙招”。再去听课时，不再一味去听去记，更多的是思考，李老师的课堂哪些环节是为了培养学生自学能力，激发学生求知欲、自主独立建构新知的；哪些环节是为了学生的议论而创设情境，在议论中揭示自己思维过程、促进学力发展的；哪些环节是为了引导学生攻克难点，启发思维，提高师生情感交流的。不断琢磨，将这些方法适当地应用到自己的教学中，渐渐地开始理解怎样上课了。

二、从经历中收获

2003年4月，笔者作为刚工作一年的新教师偶获第一次在其他地区借班上公开课的机会，课题是“平行线分线段成比例定理”。这节内容对初中阶段学生能力要求很高，现在的教材已经删减。记得笔者还是学生时，数学老师就告知我们有这样一个定理，接着就是与这个定理相关的大量练习和运用，那么，该如何体现“自学·议论·引导”教学法的思想呢？

李老师指出，这节课学生已经学习了“平行线等分线段”定理，有基础，可以通过自学，将“不等分”转化为“等分”，课初就可先让学生回顾平行线等分线段定理（如图1）。引导学生，由比例线段概念得

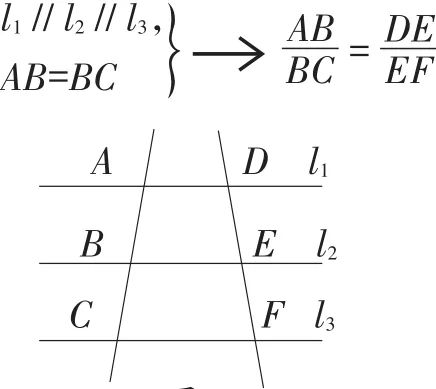
图1

同时给出问题：若AB=2BC，如何转化而证得结论呢？

学生很快自主探究找到方法——在BA上顺次截取与BC相等的线段，二次后截尽，转化为平行线等分线段，顺利得出结论。

接着进一步抛出本节课的难点——若截不尽呢？如何转化？

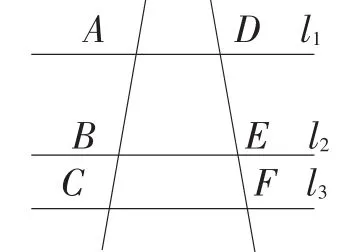
图2

让学生小组交流后全班交流，此时学生显得没有方向，该如何引导呢？如果是教者一个人讲下去，也许可以把预设顺利讲完，但这显然不是“自学·议论·引导”教学法的体现。要让学生讲，他们能讲清楚思路吗？看着下面听课的专家包括师傅李老师，都担心笔者如何突破这个难点。该如何驾驭呢？这时下面出现了一个微小的声音：“能不能把BC改短后去截？”“好，你准备将BC如何改短呢？改短后如何转化呢？”“截两次后剩余部分可以用BC截，假设再截三次截尽，则AB=2.3BC。此时过每个截点作平行线，可以将DE也分成两大段和三小段，由平行线等分线段定理可知DE=2.3EF，即（如图2）。若还截不尽，可以用更小的线段去截。”接着，在一步步的引导下，几位学生渐渐有了思路。终于在大家的努力下，学生共同概括出了平行线分线段成比例定理。今天回想起来，“引导”是多么奇妙，在踌躇关头，一个学生的小声议论打破了“僵局”，师生一起找到了难点的突破口，随之而来的追问，引导着学生找到了自己解决难点的途径。师生都在这种“互引”中找到了成功的喜悦，这便是一种“教学相长”吧!

虽然这堂公开课上得很稚嫩，课后师傅提出了不少改进的地方，但对笔者来说是一次难得的锻炼。通过这堂课，需要思考如何深入学习“自学·议论·引导”教学法，展现这套教学法的精妙，为后来的教学展示提供了经验。

渐渐地，在每次备课时都有意识地去设计、去思考，努力向“自学·议论·引导”教学法的精神靠拢，教学开始“有法”了。

三、从“无形”的类比中提升

对外展示多了，用“自学·议论·引导”教学法指导自己的教学也更多了，渐渐地笔者开始对“自学·议论·引导”教学法产生了模式化的依赖，更准确地说是自己的懒惰把这种教学法当成一种工具在机械地操作。

2009年10月，在李老师的推荐下，笔者有幸参加“名师指导团送教下乡”活动，并在活动中执教“一元二次方程”。为准确定位这节课的教学目标，深入研究李老师著作和相关课例之后，确定了如下教学目标：在与一元一次方程的类比中让学生自主建构一元二次方程的知识体系。具体实施时，先让学生回顾一元一次方程，说出它的定义、标准形式、方程的解以及解方程的步骤等，将一元一次方程知识体系放到了一张表格（见下表）中，而后学生可以对照表格依葫芦画瓢地完成一元二次方程的学习。

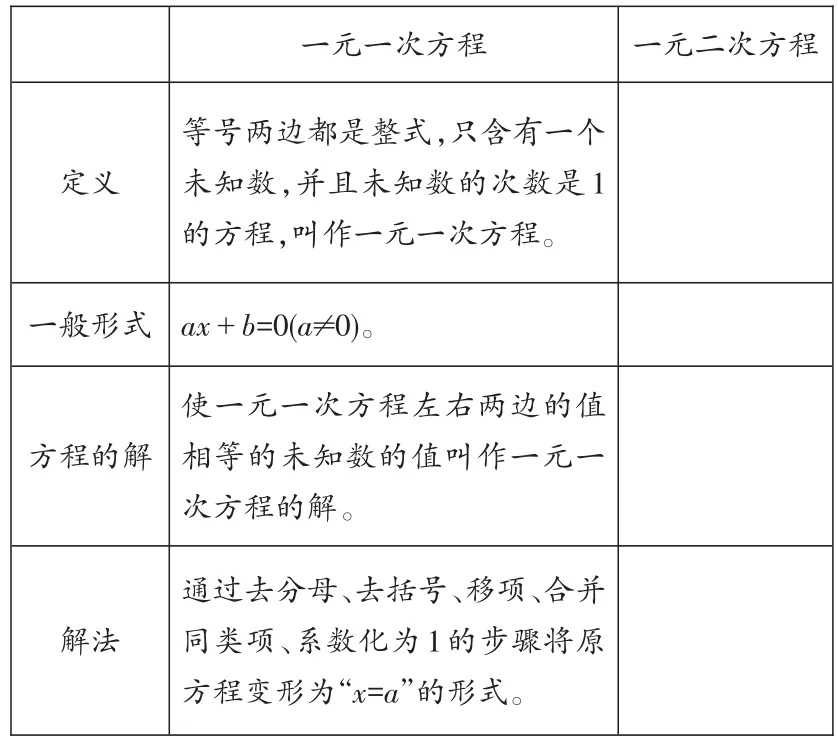
一元一次方程一元二次方程定义等号两边都是整式，只含有一个未知数，并且未知数的次数是1的方程，叫作一元一次方程。一般形式方程的解解法ax＋b=0(a≠0)。使一元一次方程左右两边的值相等的未知数的值叫作一元一次方程的解。通过去分母、去括号、移项、合并同类项、系数化为1的步骤将原方程变形为“x=a”的形式。

教案初稿出来后，笔者有些得意，遐想着上课的画面：学生套用前面一元一次方程的概念，自然地说出一元二次方程的相关知识，都不需要教师的点拨，多能体现学生的自主性呀！即便是学习能力比较弱的学生，利用这张表格的内容自学也不困难，课堂的议论该多么热烈呀！但与李老师交流后，大师的眼光就是那么犀利，她一针见血地指出：“用这样列表的方式与一元一次方程进行对比，将初三学生的思维发展限制在一个框框里，他们无法对新知进行拓展与探索，对初三的学生要求偏低了，明显滞后于学生学力的发展。”根据李老师的建议，重新备课，更换如下问题情境：

（1）一个矩形的周长是40cm，它的宽比长少6cm，求这个矩形的宽。

（2）一个矩形的面积是40cm，它的宽比长少6cm，求这个矩形的宽。

整理得到2x-14=0和x2+6x-40=0两个方程。通过对这两个方程的比较，学生由学习一元一次方程的经验，自觉给第二个方程取名为一元二次方程，接着让学生自主概括一元二次方程的定义及一般形式，学生在潜移默化中自觉地与一元一次方程类比，借助一元一次方程的学习经验和对“元”“次”的认识自主生成了一元二次方程的相关知识，通过练、议巩固了一元二次方程的定义后，学生再进一步探究什么是一元二次方程的解和如何解方程时，不断地自觉运用类比去生成一元二次方程的知识结构。整堂课我并没有与学生谈到一句“类比”，可在学生最后谈收获时，大部分学生都谈到了研究新的方程可与前面所学知识进行比较，把未知转化成已知，可见“类比”在无形中已渗透进学生的思维里，这样的教学更能让学生有所收获，不管是在知识上，还是在情感上都符合他们发展的需要，贴合他们的“最近发展区”。更可贵的是，有位学生说：“今后我们可以定义任何一个多元多次方程了，而且最终都应转化为一元一次方程来研究。”无形的“类比”又让这节课更开放了。

在后来的教学中，笔者逐渐领悟到，李老师的“自学·议论·引导”教学法从没有一个单一固定的教学模式，只是抓住了“以人为本、整体发展”的核心理念，以人为认识活动和一切实践活动的主体，确保了学生在学习活动中的主体地位，只要是有利于学生主体地位发挥的，有利于师生学力共同提高的，有利于学生情感态度和心理发展的教学行为，都是和谐的、高效的“自学·议论·引导”教学法的课堂形式的体现，正所谓“教学有法，教无定法”，想来，也就是杨九俊先生赞誉李老师教学风格是“有规则的自由”的原因吧。

在每一次成长中，笔者认识到，学无止境，要树立终身学习的理念。李老师正是用自己的实际行动影响我们的，年近八旬的她，仍然坚守讲台，不断地汲取新知识充实自己的教学理念，更何况我们年轻人呢？李老师的“自学·议论·引导”教学法的内涵和外延已如浩瀚的大海，而我们只是一叶刚刚启程的小舟，在远方依稀看到了一抹光亮。但这足以激励我不断前行，不断追求。

（作者为江苏省南通市启秀中学教师）