一道圆锥曲线试题的背景揭示及推广

杨苍洲

福建省泉州市第七中学 (362000) 林志敏福建省泉州市第五中学 (362000)

一道圆锥曲线试题的背景揭示及推广

杨苍洲

福建省泉州市第七中学 (362000) 林志敏福建省泉州市第五中学 (362000)

近年来，高考试题的命制往往具有深刻的高数背景，起点高落点低，试题设计来源于高等数学，但是用初等数学方法来解答，因此挖掘其背景，推广其结论很有必要，一方面可以让学生摆脱题海战术，另一方面可以把学生的思维引向深处.

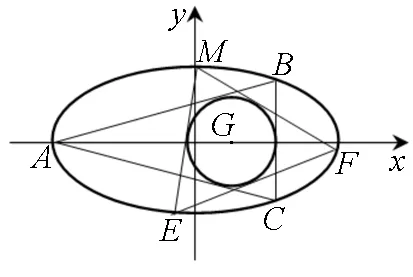
图1

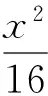
(Ⅰ)求圆G的半径r；

(Ⅱ)过点M(0,1)作圆G的两条切线交椭圆于E，F两点，证明：直线EF与圆G相切．

一、背景揭示

本题的第(Ⅱ)问是Chasles对应原理的一个应用：

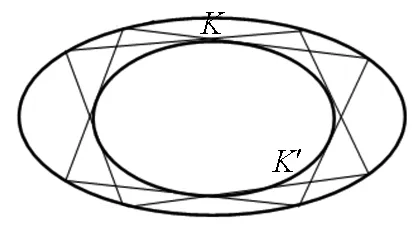
图2

不相切的两条圆锥曲线K,K′，从K上一点P0作K′的一条切线，它和K的第二个交点P1.通过P1给出K′的第二条切线，它和K的第二个交点是P2.如此继续，可以构造出链P0,P1,P2,...,Pn.

则利用对应原理有：当链曾有一次在非平凡的意义下封闭Pn=P0，则不管P0在K上如何选取，链都封闭.(如图2)

反映在本题的第(Ⅱ)问，若某个椭圆内接三角形如ΔABC的内切圆，则必为该椭圆任一内接三角形的内切圆.这里的椭圆和圆可以推广为任意两个圆锥曲线，基于难度的控制，一般限制第二条圆锥曲线K′为圆.

二、初数证明

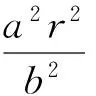
(Ⅱ)过椭圆E上任一点P作圆T的两条切线交椭圆于M,N两点，则直线MN与圆T相切.

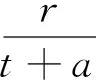
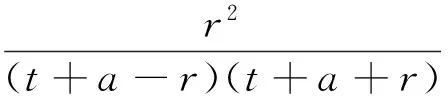
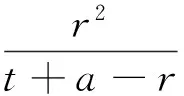
(Ⅱ)设P(acosθ,bsinθ),M(acosα,bsinα),

N(acosβ,bsinβ)(其中θ,α,β∈[0,2π)).

直线PM的方程为(x-acosθ)(bsinθ-bsinα)-(y-bsinθ)(acosθ-acosα)=0⟹(bsinθ-bsinα)x-(acosθ-acosα)y-ab(sinθcosα-

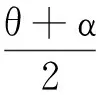
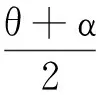
因为直线PM与圆T相切，得

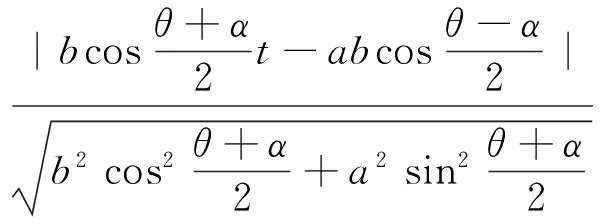
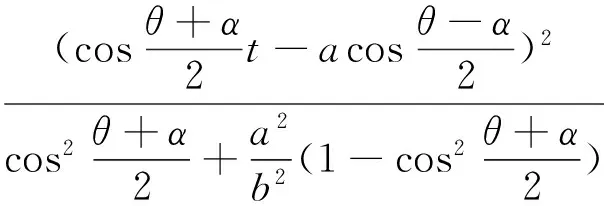
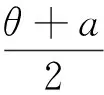
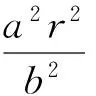
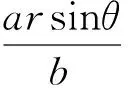
同理可得(acosθ-rcosθ-t)(acosβ)+

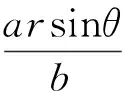
圆心T到直线MN的距离：

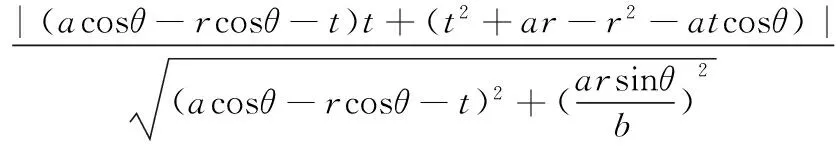
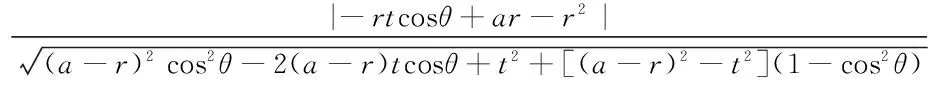
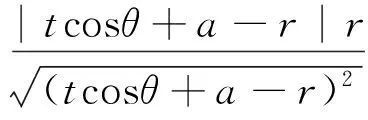
故直线MN与圆T相切，结论成立.

三、结论推广

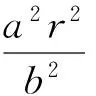
(Ⅱ)过双曲线E上任一点P作圆T的两条切线交双曲线于M,N两点，则直线MN与圆T相切.

定理3 若圆T：(x-t)2+y2=r2是抛物线E：y2=2px(p>0)的内接ΔABC的内切圆，其中A为抛物线的顶点，则有

(Ⅰ)r2=2p(t-r)；

(Ⅱ)过抛物线E上任一点P作圆T的两条切线交抛物线E于M,N两点，则直线MN与圆T相切.

以上两个定理2、3的证明，可以参考定理1的方法，留给读者自行完成.

四、变式应用

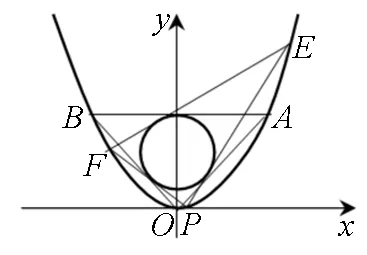
图3

变式1 如图3，已知圆C:x2+(y-b)2=R2是抛物线

(Ⅰ)建立b与R满足的关系式；

(Ⅱ)证明：过抛物线上的任意一点P(x0,y0),|x0|≠R，都可作抛物线的内接ΔPEF，使得圆C为其内切圆．

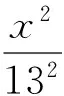
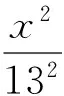
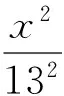
[1]彭世金.对江西卷文科第22题的探究[J].中学数学研究(江西)，2009(11)：37-38.

[2][荷]B.L.范德瓦尔登著，李培廉、李乔译[M].代数几何引论，北京：科学出版社,2008.