三角形长度元素的一条不等式链的下界改进

何 灯

福建省福清第三中学 (350315)

三角形长度元素的一条不等式链的下界改进

何 灯

福建省福清第三中学 (350315)

文献[1]中利用3个引理建立了关于三角形角平分线的一个等式

定理1 设a,b,c是ΔABC的3条边长，wa,wb,wc是ΔABC的角平分线，则

文献[4]将以上4个不等式进行统一指数推广，得到

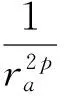
笔者发现上述不等式链的下界可作进一步的改进，由此得

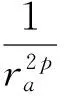
故定理3的下界优于定理2的下界.

为了证明定理3，需要引入一个引理.

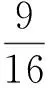
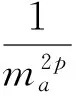
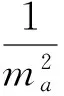
由于∑a2b2=(∑ab)2-2abc∑a=[s2+r(4R+r)]2-16Rrs2，∑a=2s，则只需证明

若4R-31r≥0，则(*)式显然成立.若4R-31r<0，则f(s2)可看作以s2为自变量的一元二次函数，由16Rr-5r2s24R2+4Rr+3r2(Gerrestsen不等式)及一元二次函数图像性质可得f(s2)≥min {f(16Rr-5r2),f(4R2+4Rr+3r2)}，又f(16Rr-5r2)=4r2(R-2r)(576R2-563Rr+118r2)，f(4R2+4Rr+3r2)=4(R-2r)(16R4+16R3r+44R2r2+33Rr3+22r4)，由欧拉不等式(R≥2r)易证f(16Rr-5r2)≥0，f(4R2+4Rr+3r2)≥0，故f(s2)≥0.得证当p=1时，定理3成立.

当p>1时，由幂平均不等式得

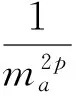
综上，定理3得证.

[1]曾善鹏.一个角平分线不等式[J],数学通报,2009(12):45.

[2]安振平.一个角平分线不等式的简证与加强[J],数学通报,2011(4):38.

[3]马占山,范红英.关于三角形旁切圆半径的一个有趣性质[J],数学通报,2011(11):57.

[4]黄兆麟.3个几何不等式的统一指数推广[J],中学教研(数学),2016(3):34-35.

[5]刘健.一个三角形中线不等式猜想的证明[J],华东交通大学学报,2008,25(1):105-108.