问题引导 关联思考 明晰本质——例说初中数学微探究的实践与思考

朱建良

江苏省太仓市第一中学 (215400) 江苏省太仓市朱建良名师工作室领衔人

问题引导 关联思考 明晰本质
——例说初中数学微探究的实践与思考

朱建良

江苏省太仓市第一中学 (215400) 江苏省太仓市朱建良名师工作室领衔人

初中数学课堂教学微探究主要着力于学生的学，是一种类似于课题研究的学习模式，微探究的教学目标指向培养学生的问题意识和探究能力，教师尝试将教学内容转变为“微探究”任务，在问题引导下启发学生主动探究，有效改善传统学习方式的缺点，基于学生的亲身经历，以疑问激发他们的求知欲望，优化学生数学思维方式和思维品质，具有提高学生学习效果和探究能力的功效．

《数学课标2011版》指出，综合与实践是一类以问题为载体，重视问题情境创设，以学生主动参与为主的学习活动．倡导教师深入用好教材、挖掘教材，并在教材内容的基础上开发微探究学习实践活动，精心设计一个微探究学习内容，充分调动学生的学习积极性，引导学生善于思考、乐于探究．笔者以苏科版九(上)数学第二章《圆》第四节《圆周角(3)——圆内接四边形》为微探究课题，谈谈在教学实践中的一些收获和认识，供同行参考．

1．微探究学习内容分析

微探究学习内容为九(上)苏科版数学§2．4 圆周角(3)——圆的内接四边形，其学习目标为：(1)掌握圆内接四边形的概念及其性质定理．(2)引导学生经历探究“圆内接四边形的对角互补”的学习过程，培养学生动手操作、自主探索和合作交流的能力．(3)培养学生合情推理意识，掌握说理的基本方法，渗透从特殊到一般、类比、转化等数学思想．

2．问题启智、类比探究

从具体的作四边形的外接圆的动手操作实验出发来设计微探究学习内容，类比作三角形外接圆的方法，激发学生的思维始终处于积极主动的状态，通过猜想、发现与归纳推理，理解数学概念．数学概念的形成过程是进行数学思想方法教学的最好载体，引导学生理解没有“过程”就没有“思想”．

图1

问题1 (1)过三角形的三个顶点能画一个圆吗？为什么？(2) 过三角形的三个顶点这个圆叫什么？这个三角形又称为什么？(3) 过四边形的四个顶点能画一个圆吗？为什么？(4) 如图1，已知四边形ABCD是⊙O的内接四边形，请探究∠A与∠C，∠B与∠D有怎样的数量关系？为什么？(说明理由)用几何语言准确表述你的发现．

解析:尝试画图实践操作入手，类比探究圆内接四边形ABCD性质，得出∠A+∠C=∠B+∠D=180°的数量关系，归纳出“圆的内接四边形对角互补”．

设计意图:关注学生微探究学习方式，引导学生自己经历思考的过程，通过交流合作和动手操作来感悟和体验知识发生、由来的过程，在学生亲身感受、体验的历程后，抓住四边形ABCD与⊙O的位置特征，运用合情推理去探索结论，从“共同特征”中归纳“本质特征”，获得数学学习经验．

3．理解性质，提炼方法

从简单的特例出发，寻求圆周角之间的数量关系，以数学知识的探究过程为学习重心，通过学生独立思考发现圆内接四边形的性质，设计动态变化的微探究问题情境，从本质上探究圆周角之间的合理联系与逻辑联系．

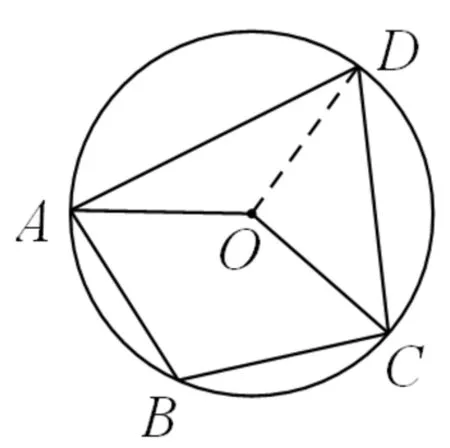
图2

问题2 如图2，已知四边形ABCD内接于⊙O，若∠AOC=140°．

求：(1)∠ABC的度数；

(2) ∠OAD+∠OCD的度数．

变式1 (续问题2)如图2，若DA=DC，你能求出哪些角的度数？

变式2 如图2，已知四边形ABCD内接于⊙O，若有ABCO，你能求出哪些角的度数？

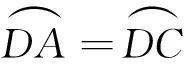
微探究问题设计基于学生数学基本活动经验，言简意赅，应用圆内接四边形性质解决问题简约明了，以特殊圆周角度数为突破口，帮助学生快速捕捉、理解有效信息、解决问题．

图3

解析:(1)连接AC，在等腰ΔDAC中，求出∠DAC=55°，解读四边形ACED内接于⊙O模型，得∠DAC+∠E=180°，求出∠E=125°.

在圆上增加一动点，将图形变换，一图多用，一题多变，问题设置别致精巧，平中见奇，微探究指向培养学生探究能力，帮助学生正确理解基本图形、基本知识，通过特殊圆周角的求解，实现知识立意到能力立意的转变．

设计意图:通过将条件弱化或增强，从而转化为微探究新问题，引导学生对数学问题进行引申、推广，促使学生积极思考，寻求最佳的解决思路，积累经验方法，培养学生自主探究、合作学习的能力．问题2难度较低，为后续探究做好铺垫，拓展问题为学生提供了展示自己智慧的舞台，使其在新问题情境中探求出解决陌生问题的方法．

4．变式探究，拓展延伸

构建“圆的内接四边形的一个外角等于它的内对角”几何模型，联系三角形角平分线和三角形相似等相关性质，采用类比联想的研究方法，及时归纳总结出解决此类问题的一般方法，帮助学生在变式的微探究的思考中发现一类数学问题的本质和规律，经历数学知识的再发现过程．

图4

问题3 如图4，四边形ABCD内接⊙O，DB=DC，∠DAE是四边形ABCD的一个外角，问∠DAE与∠DAC相等吗？为什么？

变式1 如图4，ΔABC内接⊙O，AD为ΔABC的外角平分线，交⊙O于D，连接BD、CD，判断ΔDBC的形状，并说明理由．

变式2 (续问题3)如图5，若AF平分∠BAC，连接DF，问：DF与BC有怎样的位置关系？为什么？

解析:通过寻求相等量，巧妙转化，寻求∠DAE=∠DCB=∠DBC，变式1互逆变换问题3的条件

图5

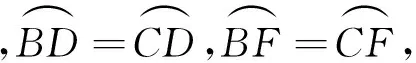
拓展如图6，四边形ABCD内接于⊙O，AC、BD相交于点F，BA、CD的延长线交于点E，若CB=CA=AE．

(1)判断BD是否平分∠EBC，说明理由；(2)若CD=6，BD=8，求DF的长．

图6

解析:依据圆内接四边形性质，寻求等腰ΔACE、ΔCAB角之间数量关系发现，∠CAB=2∠EBD，又∠CAB=

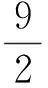
通过变式问题纵向拓展，在编制问题、解决问题、完善问题的系列操作过程中经历了数学思维的运用与逐步完善，数学微探究过程不止于数学知识的发生、发展和形成的过程，更在于数学知识、经验、思想方法的内化和迁移过程，从特殊到一般进行探究，体现数学思维中的“火热思考”，指向解题突破时要回归到“圆的内接四边形性质”的核心概念．

设计意图:基于“理解数学”的视角，通过将问题设计成同一模型多个层次的问题串，变式探究，分散难点，逐层展开，循序深入，数学微探究按图示方式展开：

真正体现了《数学课程标准(2011版)》人人学有用的数学，不同的学生在数学上得到不同的发展的理念．

5．沉淀思维，积累经验

突出能力培养应重视在问题解决中渗透数学思想方法，数学思维训练的重要目的是积累解题经验，拓展数学思维深度，优化解题策略．在思考题中以旋转变换为问题载体，涉及操作不变性思想和分类讨论的思想方法，帮助学生从特殊到一般的角度理解“化动为静、动静结合”的方法．

思考题已知在ΔABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E．(1)如图7①，若AB=6，CD=2，求CE的长；(2)如图7②，当∠A为锐角时，试判断∠BAC与∠CBE的数量关系，并证明你的结论；(3)图7②中的边AB不动，边AC绕点A按逆时针方向旋转，当∠BAC为钝角时，如图7③，CA的延长线与⊙O相交于点E，试判断∠BAC与∠CBE的数量关系是否与(2)中你得出的关系相同．若相同，请加以证明；若不同，请说明理由．

图7

设计意图:“好奇——探究——解题——感悟——创新”是数学微探究学习的必由之路，以激发学生动手操作实验为主线贯穿整个教学过程，问题设计从发散性视角培养学生的学习兴趣，因材施教，引导学生在微探究学习过程中深层地体会学习的乐趣．

课堂教学中，教师重视微探究学习的过程，微探究问题设计遵循学生的认知规律，立足于学生的实际认知水平和能力．以开放性、探究性的数学问题引导学生独立思考、合作发现，帮助学生正确理解问题，避免出现“只见教师智慧，不见学生感悟”现象，数学微探究对于学生学习方式的转变、培养学生的数学问题意识，培养学生的质疑问难的能力，具有十分重要的现实意义．

教学微探究是一种行之有效的教学方法，教师根据教材特点、学情设计微探究内容，让学生在经历知识的形成与应用的过程中，真正理解数学知识，内化知识结构，形成技能，积累方法，获得数学思想方法，通过数学微探究的学习，让学生更加有兴趣地学习知识，提升学生实践动手能力，提高数学思维模式的层次，提高教学效果，真正践行有效教学．