冷链多配送中心配送路径优化研究

梁承姬　杨继滔　黄涛

[提要] 为解决在冷链多配送中心的货物调配过程中配送中心缺货和运输成本高的问题，提出通过其他配送中心协助完成货物的调配，即横向转运策略，建立配送成本最小和顾客满意度最大的多目标数学模型。由于生鲜产品具有易腐的特性，引入惩罚函数处理约束，并对遗传算法改进。在求解中，由于配送范围内客户点多，先采用重心分区法对客户点进行分区，使得每个配送中心负责一定区域的客户点，再通过改进遗传算法优化分析带模糊时间窗冷链物流问题和多配送中心货物调配问题。最后，由算例分析，可以看出所建模型和采用的算法能够缩短路径，降低配送成本。

关键词：横向转运；重心分区法；改进遗传算法；顾客满意度

基金项目：国家自然基金资助（71471110、61540045）；上海市科委创新项目资助（14170501500、14D2280200工程中心、16DZ1201402、16040501500）；上海市重点学科资助（J50604）；陕西省社会科学基金资助项目（2015D060）

中图分类号：TP202+.7 文献标识码：A

收录日期：2017年9月6日

冷链物流配送在国外的研究由来已久，发展更是早于国内，对冷链配送和车辆路径问题的分析也较成熟完善，提出了多配送中心车辆调度的问题，即MDVRP。根据现实情况需同时考虑送货和取货，建立了带时间窗的车辆配送问题。多配送节点的车辆路径问题模型特点，给出合适的自适应的遗传算法。王科峰、叶春明将节点单需求和节点双重需求模型进行了对比分析，说明了启发式算法的改良对成本节省的实际效果。李华考虑的是约束条件未知下考虑送取货的多目标车辆路径问题。Karl F.Doerner研究了带有时间窗的送货和取货同时考虑的车辆路径问题。NabilaAzi在解决容易腐烂的食品配送的VRP优化问题上使用了距离路程最短法。于坤根据传统典型的送货和取货同时考虑的车辆路径问题为基础，构建基于该问题的城市冷链物流配送路径优化模型。结合模型设计遗传算法求解其具体配送方案。陈冲就生鲜农产品的车辆配送问题进行了研究，基于软时间窗约束条件，考虑产品的货损周期，采用节约法对模型求解和分析。如果物流网络采用库存集中管理模式，还需要考虑集中库存的再分配问题。横向转运可实现配送中心之间的物资再分配。横向转运是物料在同一层级的设施间定向运动达到补充库存的目的。例如，从供应商到制造商，从制造商到分销商，层间流动的方向和物流比较容易确定。相比之下，横向转运是更为灵活的库存补充再分配方式。

本文结合当前配送路径的研究以及对横向转运的概述，考虑到冷链物流承载的货物具有一定的特殊性且对温度的要求较高，提出在冷链物流配送中设定模糊时间窗来反映顾客满意度。同时，探讨了多配送中心的冷链物流存在的某一配送中心无法满足某一需求点的货物调配问题，在该问题的研究中，以配送点至客户点、配送点之间的成本和顾客满意指标来设立多目标模型。为优化多配送中心的配送路径，在求解中，先采用重心分区法对客户点进行分区，使得每个配送中心负责一定区域的客户点，再通过改进遗传算法优化分析带模糊时间窗冷链物流问题和多配送中心货物调配问题。由算例分析可以看出所建模型和采用算法的研究意义。

一、问题描述

由于当前城市规模不断扩大，消费者对物流配送的需求明显升高。从物流配送方面考虑，客户点呈现逐年增多、区位复杂的特点，通过对客户点分区，设立多配送中心進行物流配送，可以避免配送车辆线路杂乱、时间长、成本高的缺点。同时，随着电子商务量和人们生活水平的提高，物流配送需求越来越大，配送中心的供货压力也较以往增大。在现实生活中，配送中心往往存在库存不足、客户点需求增加等情况，通过考虑配送中心的货物调配，对多个配送中心的货物需求进行实时监测，及时补货可以减少对相应客户点的配送时间，降低成本。

本文考虑的基于多配送中心货物调配的冷链运输优化问题，即在一定区域范围内，有若干需要配送的客户点和多个配送中心，且配送中心有确定的配送范围。在配送中心发车向该配送范围内的客户点配送冷链货物的过程中，车辆需要在约定好的时间约束范围内完成配送，不符合实际约束就会有不同程度的惩罚成本。每个配送中心的库存是固定的，在分区后，由于个别配送点的配送压力增加或需求变化，会出现配送中心A库存不足或者客户点需求增加的情况，导致无法完成对某个客户点a配送的情况，此时将进行判断并进行选择：（1）邻近的配送中心B完成该区域配送后再对客户点a进行配送，然后返回配送中心B；（2）配送中心B补货给配送中心A，配送中心A再对客户点a所属路线进行配送。选择时间成本、距离成本较小的方案进行配送。该方法可以针对库存不足或需求增大做出相应合理的配送方案，从时间、货物质量等方面考虑都得到了明显改善。关于整个流程的车辆配送时序图，如图1所示。（图1）

二、模型建立

（一）基本假设。（1）各个客户需求点位置和需求已知，各负责仓储配送点的位置已知；（2）所有有需求点客户点的配送任务都要完成，并且只能通过一辆配送车对每个配送路径上的点服务；（3）配送车从仓储配送点出发开始服务，完成后返回出发点；（4）配送中所有的运输距离都满足小于配送运输车辆的行驶距离约束要求；（5）配送中心需要补货由其他配送中心进行调配，车辆在完成补货后返回发车配送中心。

（二）参数定义。k：配送的车辆总数，v∈k；M：配送中心点，m∈M；n：接受配送的客户点；fm：配送中心m配送货物的冷链成本；a：配送车辆单位距离成本；b：配送车辆单位空载成本；pi：客户点i需求货物的价值；？着：冷链货物的货损率，？着=1-e-？茁；qm：配送中心m对冷链货物的需求补货量；dij：配送中心i为配送中心j货物调配距离；S■■：车辆v到达客户点i的时间。

（三）决策变量。S■■：配送中心m的车辆到客户点i的时间；h■■：当配送中心i负责配送中心j的货物，调配为1，否则为0；r■■：当配送中心i调配车辆m至配送中心j为1，否则为0；x■■：当车辆v由配送中心m从客户点i配货至客户点j时，为1；否则为0；y■■：客户点i由配送中心m配送为1，否则为0；A■■：等于最佳服务时间下限ei减去到达时间S■■；D■■：等于到达时间S■■减去最佳服务时间上限li。endprint

（四）目标函数及约束条件

目标函数：

MinLP1=■■■■x■■（f■+ad■）+■■■ah■■d■+r■■+f■ （1）

MinLP=-■ （2）

约束条件：

f■=■y■■p■？着+■■？姿A■■+？姿D■■ （3）

■■y■■=n （4）

■■■x■■=n （5）

■■q■x■■+q■h■■≤Q （6）

■■■x■■+h■■≤■ （7）

■x■■=■x■■？坌m∈Mv∈k （8）

A■■≥e■+l■ （9）

D■■≥S■■-l■ （10）

A■■≥0，D■■≥0 i∈n，v∈k （11）

x■■∈{0，1} ？坌i∈n，j∈n，v∈k，m∈M （12）

h■■∈{0，1} ？坌i∈n，j∈n，m∈M （13）

y■■∈{0，1} ？坌i∈n，m∈M （14）

本文建立的是基于模糊时间约束的多目标冷链运输路径优化模型。模糊时间窗的设立表示车辆应尽量在顾客要求的时间窗内服务，但不同于对固定时间窗的硬性要求，对大多数非刚性需求时要求服务时间外也可以进行服务，以部分成本作为惩罚，同时将车辆服务时间用顾客对服务的满意程度来表达，更加直观全面的描述分析需求。车辆对客户点配送的不同情况如图2所示，每个客户点都有一个最优服务时间[ei，li），在此服务时间内没有时间惩罚成本且顾客满意度最高，同时在模糊时间窗[ei'，ei）和[li，li'）内会产生时间惩罚成本且影响顾客满意度，模糊时间窗之外的任何时间，客户点将拒绝接受服务，需要车辆等待至模糊时间窗内或者重新服务，最后每个顾客的服务结束后回到原配送地。（图2）

本文对模糊时间窗分析设定如下：

G（Siv）=0 Siv∈[0，ei'）■ Siv∈[ei'，ei）1 Siv∈[ei，li）■ Siv∈[li，li'）0 Siv∈[li'，∞） （15）

在该公式中，车辆进行配送的时间被分层五部分。在[0，ei'）和[li'，∞）区间内，客户对配送服务的满意度为0，拒绝接受服务；在[ei，li]区间内，客户对配送服务最满意，此时不需要考虑惩罚产生的额外成本；在[ei'，ei]和[li，li']内，车辆也可以对顾客进行配送，但需支付一定的惩罚成本，同时顾客满意度随Siv的具体时间来确定，需要注意的是，由于延迟服务所耗的时间更久，且顾客更不希望等待车辆服务，所以设定延迟服务额外成本大于时间窗服务的额外成本。

上述模型的目标函数为两个：一是降低冷链运输中的成本；二是提高顾客对配送服务的满意程度。式（1）表示降低冷链运输中的成本，由两部分组成：一是配送中心向各个客户点配送的成本，包括冷链成本和距离成本；二是配送中心间的货物调配产生的成本，包括距离和空载成本、货损成本、惩罚成本；式（2）表示建立求解顾客对配送服务的满意程度最大化目标函数；式（3）表示车辆在向客户点配送货物时产生的冷链成本，包括货损成本和时间窗惩罚成本；式（4）表示一个配送中心负责一个需要配送的客户点；式（5）表示所有有需求点客户点的配送任务都要完成；式（6）表示冷鏈配送和货物调配的需求都不会大于车辆总载重；式（7）表示配送和货物调配所需的车辆不大于总车辆；式（8）表示冷链运输车辆从配送中心出发点发车，经过一个或多个客户点后返回发车的起点；式（9）表示当车辆提前于已知确定的时间窗约束到达，计算出的提早服务时间；式（10）表示若车辆晚于已知确定的时间窗约束到达，计算出的延迟服务时间；式（11）表示提早服务时间和延迟服务时间是非负的，即保证模糊时间窗存在；式（12）、（13）、（14）表示使决策变量值为0或1的整数限制式。

三、算法求解

（一）多边形重心分区法。本文采用多边形重心分区法，充分考虑了多配送中心的情况，先连接所有配送中心的坐标点，形成一个封闭的多边形，通过计算求得其重心坐标，再将中心坐标与多边形的每条边的中点相连并向外形成射线而把配送范围分成一个个不同的配送区域。每个区域各自有对应的配送中心，负责该区域的配送服务，不同范围的配送任务不干扰、不交叉。（图3）

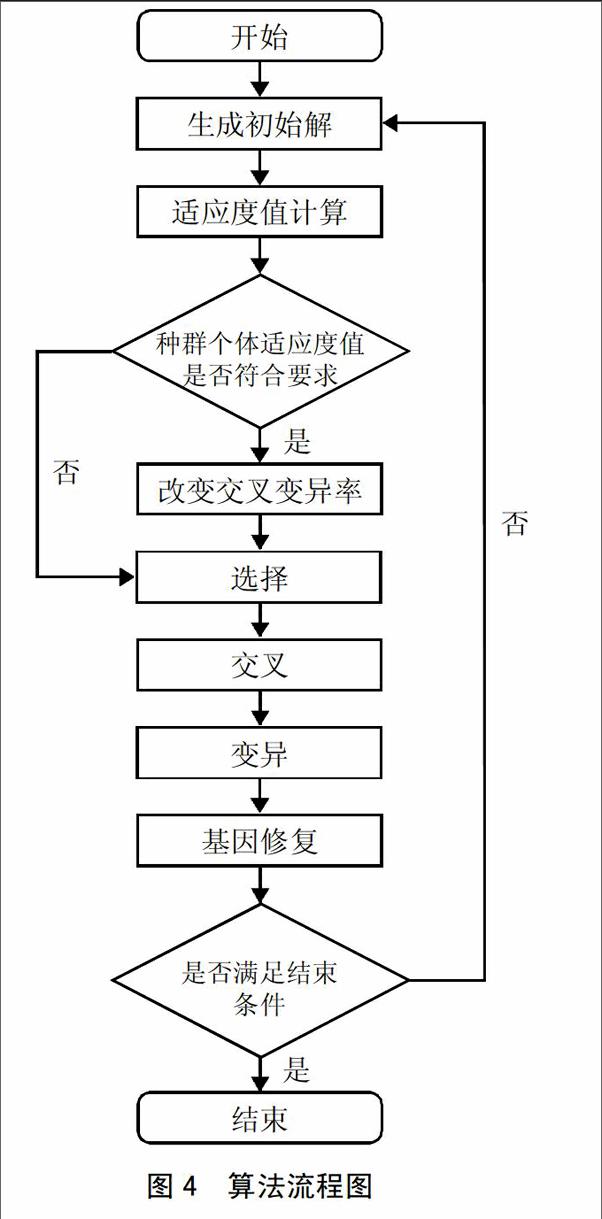
（二）遗传算法求解。在本章节对车辆路径优化求解中，第一阶段将若干客户点进行了合理的分区，在第二阶段，本文采用遗传算法对具体的配送中心为客户点运输服务的路径问题以及配送中心货物调配的问题进行优化求解。通过在算法操作中，对个体适应度值的判断，不断改变交叉率和变异率，并且在操作结束后进行基因修复，可以有效防止早熟现象的发生，避免操作后的染色体不符合约束，确保算法求解的稳定性。如图3所示整个算法的流程图，在确定个体适应度值后，做出相应判断，如果趋于一致则增加pc和pm概率。若较为分散，就减小pc和pm概率。在选择交叉后的基因修复可以有效地防止染色体不符合约束条件，确保算法求解的稳定性。（图4）

1、染色体编码。假定有m个配送中心为n个客户点进行运输。染色体第一部分为每个配送点发出车辆1，依次遍历相应客户需求点，然后返回配送起点的路径。现有3个配送点和25个客户需求点，假设染色体第一部分的编码设计为12-9-21-3-14-23-5-19，该染色体编码就是一个可行的运输方案。首先通过分区，确定每个配送中心要为哪些客户点运输服务。配送中心1的第1辆车m11负责的客户点分别是12、9、21，配送中心1的第2辆车m12负责的客户点分别是3、14、23、5、19，则该染色体是已分配好客户点的配送中心1的配送方案，通过解码可以得出属于该染色体编码的具体方案为：m11-12-9-21-m11m12-3-14-23-5-19-m12。同理，根据该操作可以得到关于配送中心2和配送中心3配送方案的染色体编码。整体的染色体编码如：12-9-21-3-14-23-5-19-0-18-10-2-13-24-7-1-20-0-17-25-6-15-8-16-22-4-11。endprint

2、生成初始种群。本章算法设计中，通过随机生成若干染色体来构造初始种群。任意取n个基因数（n=客户点数量），将这n个基因数随机设定在不同的染色体基因位中，这样就生成了冷链运输路径的服务方案。

3、交叉算子。本文所进行的交叉算子操作如图所示，首先，从父代1里任意选取3个基因位上的基因值，将其复制到子代相同基因位上；然后去掉父代2中与父代1所选基因值相同的基因；最后子代1中的基因位值由父代2里仍保留的基因有序填充，如果遇到某一基因位上已经存在基因值，则跳过该基因位继续填入下一个位置。本章选取的交叉操作方法如图5所示。（图5）

4、变异算子。在遗传操作中，变异算子遵循一定的变异概率，模仿生物学中基因突变原理，为了开拓染色体不同组合的多样性，从而进行染色体变异。如图5，这里选取父代中的两个随机基因，进行调换，从而达到变异的效果，产生新的子代。（图6）

5、适应度函数。作为遗传算法衡量染色体个体的优劣准则，适应度函数充分结合了问题本身的要求和考虑约束，一般与目标函数需要紧密相连，才能作为判断标准的主要依据。本文综合考虑将目标函数作为适应度函数。即Fi=minLP1-100·n（minLP2）的形式。其中，目标函数LP2是0～1内的小数，代表客户对服务的满意程度，对适应度函数的影响程度较小，所以选择100作为变换因素，将顾客满意度转化为费用。

6、基因修复。本文考虑的是基于配送中心货物调配的冷链车辆路径问题，在交叉和變异操作后，会由于条件和约束限制，染色体会出现不符合规则的情况。故针对不符合条件的染色体进行如下步骤的基因修复：

第1步：判断交叉变异后的染色体中，所有配送中心每辆车配送的客户点是否大于等于2，如果是转入第二步，如果不是则放弃该染色体重新生成，再次判定。

第2步：由于染色体中含有没有意义的数字为0的基因位，所以判断在交叉变异后是否存在间隔符0相邻的情况，这种情况会导致有车辆闲置，配送中心无配送任务，若不是转为下一步，若是则随机选取其他基因位随机段插入两个间隔符0之间。

第3步：判断染色体中包含间隔符0的数量是否等于3，等于则符合条件，不等于会生成少于3个配送中心的配送方案，任意选取两个基因位间插入一个间隔符0，使染色体符合条件限定。

四、算例分析

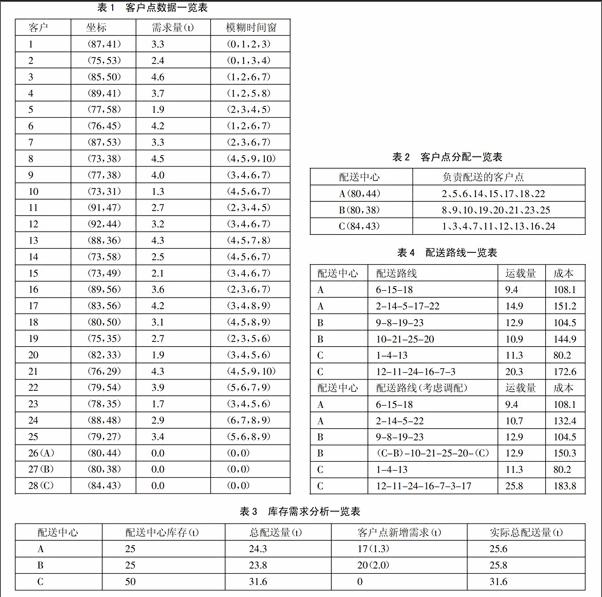
（一）算例介绍。假设配送中心数量为3个，有25个需要运输服务配送的客户点，客户点经过分区已确定由哪个配送中心配送。车辆每公里运输成本为2元，冷链中的货损率为7%，冷链货物的价格为1，500元/t，？姿1=0.5，？姿2=1.0，？茁=1.0。本章节模糊时间窗ei'，ei，li，li'。ei，li是指顾客对运输服务满意度为1的时间窗，把该时间窗各项两端扩展1h，即ei'=max{0，ei-1}，li'=li+1。在25个客户点后，标号为26、27、28的分别代表3个配送中心A、B、C，库存量分别是25、25、50。具体初始数据如表1所示。（表1）

通过分区，得出各个配送中心负责的客户点，具体如表2所示。（表2）

在实际配送算例中，部分客户点因市场原因会出现需求增长，如表3所示，属于配送中心A的客户点17新增了1.3t的需求量，属于配送中心B的客户点20新增了2.0t的需求量，这也使得实际总配送量发生改变，对比配送中心的库存量，则需要进行货物调配才能完成每个客户点的配送。（表3）

对于算法中相应的参数设置为：N=100，迭代数为200，pc=0.8，pm=0.05。通过Matlab运行求解。

（二）不考虑调配的优化方案。首先得出一个不考虑客户点需求增加，不需要货物调配的配送方案，如图7所示。（图7）

在图7所示的配送方案中，选取一个距离3个配送中心距离接近的点作为一个虚拟发货点，这样由虚拟发货点向3个配送中心延伸，再进行路径优化。虚拟发货点延伸的路程成本不算在总成本内。由于事先进行的分区操作，使得整个区域的客户点配送路径更加合理清晰。

（三）考虑横向转运的优化方案。在考虑客户点需求增加后，发现负责A配送的客户点17和负责B配送的客户点20出现需求变动，两个配送中心皆不能完成对相应需求变动的客户点的配送，因此需要由库存充足的配送中心C进行货物调配。为了保证符合目标函数成本最小的条件，在确定货物调配之前需要对不同的方案进行对比判定。

方案1：C在完成负责区域的配送后，继续为客户点17配送货物再返回C。

方案2：C将货物配送至A，货物调配车辆再返回C，仍由A为客户点17进行配送。

新增的货物需求导致配送中心无法按原计划进行配送，确定新的配送方案需要根据不同路线距离成本的对比来决定如何选择。通过对图7的配送结果图中可以分析出，方案1因配送客户点17，需要走的路径为3-17-C，再减去原本3-C的距离，同时省去了配送中心C中5-17-22的路程；方案2需要走的路径为C-A-C，其他路径不变。可由距离计算公式d=■得出距离的对比结果。客户点20的判断方法同理。（图8）

图8是判断配送方案后的优化结果，客户点17由配送中心C的分支路线配送，在配送中心C将货物运送至B后，客户点20仍由配送中心B进行配送，优化后的配送方案具体配送路线和成本对比如表4所示。（表4）

五、小结

为了解决在冷链多配送中心的货物调配过程中，配送中心缺货和运输高成本问题，提出通过其他配送中心协助完成货物的调配，即横向转运策略，建立配送成本最小和顾客满意度最大的多目标数学模型。由于生鲜产品具有易腐的特性，引入惩罚函数处理约束，并对遗传算法改进。

本文中在不考虑客户点需求变化之前的总运载量为79.7t，总成本为761.5。加入需求变化考虑因素，客户点17和客户点20分别增加需求1.3t和2.0t，同时判断配送路线成本，在优化后选择的配送路线总运载量为83t，总成本为759.3。可以看出，在总运载量提高的前提下，通过路线优化，成本反而得以下降。

主要参考文献：

[1]Laura Calvet，Albert Ferrer，M.Isabel Gomes，Angel A.Juan，David Masip.Combining statistical learning with metaheuristics for the Multi-Depot Vehicle Routing Problem with market segmentation[J].Computers & Industrial Engineering，2016.8.

[2]Chao Wang，Dong Mu，Fu Zhao，John W.Sutherland.A parallel simulated annealing method for the vehicle routing problem with simultaneous pickup delivery and time windows[J].Computational Optimization and Applications，2015.4.83.

[3]郑翀.基于自适应遗传算法的多配送中心车辆调度优化[D].辽宁：大连海事大学，2013.

[4]王科峰，叶春明.节点具有双重需求车辆路径问题及其解的性质分析[J].上海理工大学学报，2013.35.4.

[5]李华.具有同时配送和回收需求的车辆路径问题研究[D].四川：西南交通大学，2007.

[6]李宏.城市冷链物流配送车辆路径问题的研究[D].湖南：长沙理工大学，2006.

[7]Herer，Y.T，Tzur，M，Yucesan，E.The multil-ocation transshipment problem[J].IIE Trans-action，2006.38.endprint