基于两种教育公平理念的数学教学公平

摘 要 当下有关教育公平的概念大都折射出尊重权利和尊重差异这两种公平理念。受其影响，数学教学在课堂资源分配、数学教学和评价中分别形成了“均分”原则与“应得”原则、授受式与活动式以及多元化与标准化矛盾。小组合作式学习以及形成合理的数学学习评价观念是协调这些矛盾，从而实现数学教学公平的有效途径。

关键词 尊重权利 尊重差异 数学教学公平 协调矛盾

一、教育公平理念与数学教学公平

1.教育公平的两种理念

在诸多关于教育公平的观点中，大都折射出两种公平理念：一是尊重权利说，二是尊重差异说。尊重权利是指受教育权是人的基本权利之一，教育公平要着重保护人的这一权利。体现尊重权利的典型理解是：教育公平是教育“质”的范畴，是相对的；在教育活动中公平对待教育对象及其评价；教育公平包含平等性和合理性，其观念基础是平等理念；教育起点的平等是教育权利的平等；教育平等不应被理解为教育上的“相称”[1]。此种观点强调教育公平是相对的，其本质应体现社会平等、比例平等或实质平等，在基础教育阶段，受教育是人的基本权利，这种权利的获得不需要竞争，各级教育机构要予以绝对的保证。与之相比，高等教育则有所不同，属于人较高的权利，只能实现比例上的平等，使有能力接受此阶段教育的学生都享有均等的机会。而“相称”体现的是教育对象个体特性的“应得”需求，对人的基本权利做出了人为的修改。尊重差异是指教育公平要体现人的差异性，将有限教育资源进行高效使用，使人得到应有及充分的发展。体现尊重差异的典型理解是：在教育公共资源的配置或供给过程中按照“其所应得”原则使资源与教育对象形成“相称”关系，充分实现教育资源的平等、均衡、合理安排与有效利用[2]。据此，教育公平就是要体现对个体差异的尊重，要求公平的同时还要兼顾效率和质量，但问题是：如何裁定“其所应得”？由谁来裁定？

这两种教育公平理念有所重叠：首先，二者都认为教育公平是相对的，是对质的考量；其次，教育公平的目的就是要实现公共教育资源的合理分配。可见这两种理念在教学中产生的矛盾是辩证统一、可调和的。根据教育公平所要调节的教育资源分配在教育过程中的地位，将教育公平分为起点公平、过程公平和结果公平。首观起点，受教育权是个体享有的基本权利之一，为彰显人权不可因个体的特性而对这一权利进行调整。再观过程，教育公平不能只顾及权利的平等，在保证机会平等的同时还要保证质量，即人人都可得到充分发展的机会，使教育的收益最大化。正因如此，有人提出了教育公平的差异原则、平等原则以及补差原则[3-4]。与前面两点相比，结果平等是乌托邦似的构想，由于个体存在差异，每个人的成就不一样，不可能整齐划一地对学生进行要求。

2.数学教学公平

教学公平是教育公平的子系统，是实现教育起点公平之后所面临的又一难题。教学发生在学校中，进入学堂的学生都已获得受教育权，而这一权利却是初步和可视的，在教学活动中学生还需获得实质的、隐性的受教育权利。数学教学公平是指学生学习数学以及参与数学教学活动的机会均等[5]。法律、政策只能将学生送进学堂，学生坐在教室里并不一定就有数学学习的机会。数学学习机会隐藏在数学教学过程和学习结果的相互影响中，学生能否拥有公平的数学学习机会，就要看数学教学能否对课堂学习资源进行合理配备，以及在学习结果上给予应有的保障。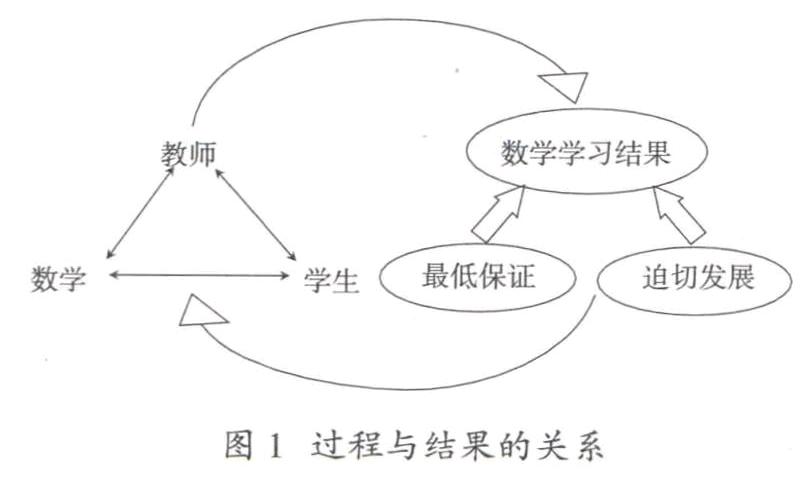

数学教学围绕着教师、学生和数学三者之间的相互作用而展开[6]。学生能否参与课堂数学学习的关键就在于他們对课堂学习资源的掌握情况。课堂学习资源主要表现为师生互动、生生互动以及数学实际操作，其中最为重要的是数学实际操作的机会。在实际操作中学生能够培养他们作为数学学习者和操作者的意识，使学生认识到自己就是数学学习的主体。数学学习的主体意识促使他们在数学学习中努力参与，并对自己的学习过程进行有效监督，独立地形成数学认识。学生的实际操作还离不开师生、生生之间的互动，在互动的过程中，给学生的操作提供指导，避免走弯路或形成不当的认识，还有助于学生发生联想，使数学的认知结构更加完善。

数学学习结果的公平主要表现在两个方面：保证每位学生掌握能够使其继续学习数学的基础知识和基本能力；使每个学生在数学上获得适切的发展。虽然对数学学习的结果不能提出整齐划一的要求，但要有统一的最低要求，即每位学生必须掌握使其继续学习数学的基础知识和基本技能。同时，还应使学生根据自己的能力在数学学习上得到适切的发展，因此，数学学习结果的评价要实现帮助学生发现其学习上的不足，还要培养他们的信心和兴趣，尽可能获得更多的学习数学的机会。

综上所述，课堂教学是对学习资源进行分配的过程，数学学习结果是对课堂学习资源进一步分配的依据。数学学习机会蕴藏在过程与结果的交互影响中，好的数学教学过程产生良性的数学学习结果。良性的数学学习结果是进一步数学学习的基础，并且能够保证学生的兴趣与信心，服务于下个阶段的数学学习，其关系如图1所示。

二、两种教育公平理念下数学教学中的矛盾

数学教学过程与数学学习结果的良性循环可实现数学学习机会的平等。在注重权利与注重差异这两种公平理念的影响下，数学教学形成了“均分”原则与“应得”原则、活动式与授受式和多元化与标准化矛盾。

1.数学课堂资源分配之“均分”原则与“应得”原则

（1）“均分”原则的利与弊

课堂教学资源的平均分配是对学生受教育权利的尊重。褚宏启教授认为不止要让所有的学生享受均等的教育机会，还要让他们在教育过程中享受同等的高质量的教育[4]。人人享受均等的高质量教育，这是教育公平的最高境界，使人的权利得到充分的尊重。只有在教育资源相当充足的情况下才能实现这种理想的教育公平，但在资源有限、人数众多的课堂中这种公平是很难实现的。然而，低质量的均等不是教育公平，通过提高教育质量促使不同学生学习得到长足的发展才是教育公平追求的实质性目标[7]。endprint

（2）“应得”原则的利与弊

应得原则使每位学生分得的课堂资源与各自内部条件形成“相称”的对应关系。这种分配方式充分尊重了人的差异性，使有限课堂资源得到了充分应用。我国通过托低拔尖来提高总体的教育质量，是一种高效培养人的教学方式。但面临的问题是：如何界定每个学生的“应得”，如何做到公正的“应得”分配；如何消除这种分配方式对学困生受教育权利的威胁。

2.数学教学过程之授受式与活动式

（1）授受式教学的利与弊

授受式教学是指教师将教学内容按由浅到深、由具体到抽象的层次进行划分，并对教学的重难点进行估计，用准确的语言进行讲解，使学生能够用已有的、相关的数学知识将其同化与顺应。授受式教学给每位学生呈现同样的数学学习资源、学习目标；教师还可以凭借专业性注意对学生的状态进行有效地控制，一定程度上避免学生的假性参与，从而保护了学生的数学学习机会。授受式教学的公平隐患表现在三个方面：第一，无法实现因材施教。个体差异使部分学生不能适应统一的教学方法与教学内容，如此便剥夺了这些学生的数学学习权利，采取统一的教学目标易使部分学生产生挫败感，对接下来的数学学习产生不良的影响。第二，教师的专业性注意容易失效。在教学中教师容易受情感和情绪的影响使专业性注意的功能不自主的丧失，如教师被活跃的学生吸引而忽视较为安静或走神的学生。第三，漠视学生的主体地位。剥夺了学生在数学学过程中的实际操作的机会，阻止了学生对数学的自主建构，不利于数学学习反思能力的培养以及数学CPFS结构的形成与完善。

（2）活动式教学的利与弊

活动式教学是指教师创设教学情境，允许学生凭借学习的内在需求，采取主动探索、变革、改造活动对象等手段来实现自己主体能力的综合发展[8]。活动式教学将数学认识由“静态”转化为“动态”。这种教学方式尊重学生的差异性，允许他们采用自己擅长的方式去学习数学，在参与的过程中每个人都会有“新的”发现，每个人都有所得。活动教学的缺陷主要表现在两方面：一方面，容易产生边缘化的学生。部分优生由于过硬的数学基础和学习能力，使得他们在数学学习活动中掌握着话语权，而处于劣势的学生由参与者变成了旁观者，久而久之，数学学习资源都集中在了这部分优生的手中，间接的剥夺了处于劣势的学生学习数学的机会。另一方面，难以保障学习结果的最低要求。数学的活动式教学注重学生的自主建构，但由于学生的基础与能力不同对数学理解的程度也就不同，而被边缘化的学生更难以形成继续学习数学的必要基础。

3.数学学习评价之多元化与标准化

（1）多元化评价的利与弊

多元评价强调方法多元、评价主体多元、评价内容多元，其本质在于全面真实的评价学生的学习成就，反应学生学习上的问题，为教学的改進提供信息，最终促进学生的全面发展[9]。数学学习多元化评价是指方法上既定量又定性，评价主体上既师评又生评，评价内容上既重数学知识又重数学能力、既重数学技能又重数学情感态度与价值观、既重数学学习结果又重数学学习过程。多元化评价将学生的学习结果立体的展现出来，充分尊重个体在学习数学上的差异及兴趣以及不同的学生在数学学习上取得的不同成果。多元化评价的价值不只是为了体现差异、对学生进行甄别，重点是对学生进行激励与诊断，从而保护学生数学学习的机会。多元化评价的缺陷是：由于评价内容没有明确的标准，因此无法形成直观的评价结果，以至很难对学生进行数学学习的纵向比较，也不利于判断学业达标程度以及未来数学人才的培养和选拔。

（2）标准化评价的利与弊

标准化评价主要表现为在评价内容上重视认知目标或者是学业成绩；在评价方法上还是纸笔测试一统天下；在评价目的上突出差异与甄选[10]。这种评价方式简便可行，有着明确、统一的标准，测试学生数学学习的结果便可知能否进入下一步学习。标准化评价是选拔人才实现学习机会的比例均等，从而高效使用高等教育资源的有效手段。这种评价方式的公平隐患表现为：第一，忽视评价的诊断功能。采取一刀切的手法对学生划分等级，使学困生不仅获得数学学习的挫败感，而且对他们数学学习的改进并无多少帮助，进而对接下来的数学学习产生负面影响。第二，忽视学生的其他成就。评价内容上的单一使得学生在非智力方面的成就被忽视，久而久之对数学形成片面的认识，逐渐失去学习数学的兴趣。第三，忽视了教学之“可能性”。统一的评价标准使数学教学成为“肯定性”教学，阉割了学生在数学上发展的各种可能性，这对兴趣广泛、特长多样的学生而言是不公平的。

三、协调数学教学中三组矛盾的策略

1.小组合作学习

数学教学公平问题围绕着数学课堂资源的如何分配而展开，要实现数学教学公平就要协调这两种理念在分配原则与方式上所产生的矛盾。第一，通过“平等优先，余补缺，优帮差”来协调原则上的矛盾。不能以任何借口对个体的受教育权进行调整，在资源分配原则上首先应该体现教育的起点公平；由于学生个体的差异，平分资源使得部分学生的资源呈现富余和不足，此时采取“余补缺”将部分学生余出的资源转移到资源不足的学生手上，使其得到适切的发展；获得更多资源的学生在数学学习上取得更好的成就后要“优帮差”，反过来帮助学习共同体中表现较差的学生。第二，通过“活动与讲授有机结合”的教学方式来协调分配方式上的矛盾。“活动与讲授有机结合”就是要实现学生主体与教师主导的统一。尊重学生学习的主体地位、允许他们根据自己的特性采用适合的方式去使用资源是对个体差异性的尊重。然而，教师还要发挥其主导作用进行调控以实现如下三个目标：使每位学生能够顺利地使用这些资源；将多余的资源进行重新调配，满足学生的适切发展要求；对学生是否符合进一步数学学习的最低要求进行把关。

“平等优先，余补缺，优帮差”原则以及“活动与讲授有机结合”教学方式的平台是小组合作学习。在数学教学过程中，学生的学习离不开实践、交流和指导。塑造出来的“任务性兼互助性”小群体可以充分发挥学生的主体作用，使学生有更多的交流以及实际操作机会。同时，化整为零而成的若干非正式小群体便于教师的专业性注意发挥作用，在小组中教师能很好的注意到每个学生的表现，对整个教学做出合理的调控。然而小组合作学习教学的另一关键之处在于学习情境的创设。数学教学离不开问题解决，出于公平的考虑，任务情境中的数学问题在难度上要呈现出梯度以满足不同学生的发展需求，保证学生能够参与。在实施的过程中还要注意以下三点。endprint

其一，防止学生边缘化。在小组合作式学习中，“组内成员任务技能的结构”和“任务的特殊分配”是防止小组成员被边缘化的有效手段[11]。在需要多种技能联合操作才能完成的任务情境中，通过“小组成员任务技能的构造”手段使学习小组具备完成某项任务的全部技能，但小组每位成员需要各展所长才能完成任务，这样不仅保证学习小组任务完成的可能性，而且使小组中的每一个成员变得无可代替，促使他们发生更多的交流与合作。“任务的特殊分配”手段指的是在活动过程中，教师凭借专业性注意发现小组中疑似被边缘化的学生，并且公开给他们分配特定的任务，保证小组接受他们，并且承认他们的地位。

其二，提高教师的专业性注意。传统的教师注意停留在学生参与与否、学生得出的结果正确与否，为实现数学教学公平，教师的专业注意还应该关注学生学习策略的选择，关注并理解学生的认识以及对学生的认识做出反应。也就是将教师的专业性注意的集中点转移到学生内部的学习过程。

其三，情境化与去境脉化相结合。教学的去境脉化就是要帮助学生对完成任务的过程进行反身抽象，一方面使学生形成的数学认识便于在下一阶段的学习中进行迁移，另一方面对学生认识予以保证，以满足数学学习的最低要求。

2.形成正确的数学学习评价观

多元化评价或标准化评价不是指具体的某一种评价方式，而是突出评价的视角和出发点，欲协调这对矛盾首先要了解：多元化与标准化的目的是什么；数学学习评价的目的是什么。多元化评价并不是排斥测试偏重主观的评价，而是以测试为基础加入多种元素、拓宽评价维度，以达到量评与质评相结合的效果，实现对知识、能力、情感态度以及过程等的全方位评价，其目的在于促进学生的全面发展。标准化评价的目的在于从结果的维度来量化教学的达标程度，以及凸显差异性实现教育机会的比例平等。在多元化与标准化两者之间怎样取舍就要看数学学习评价的目的是什么，这就涉及到评价者采取的数学学习评价观念。从个人与社会发展的需求来看，合理的数学学习评价观念至少具有以下两点认识。

其一，评价要使人人可终身学习和使用数学。数学学习评价不能只简单的评价认知结果，而是要拓宽到数学的方方面面。数学学习评价要发挥本应该有的诊断、反馈、定向、证明和教学功能，让学生形成学习和使用数学所必须的知识、能力、思想和活动经验，以满足终身学习的需求。从数学在现代科学发展中扮演的角色来看，这才是对人权的尊重。

其二，评价要为社会培养专门人才。这种评价观就是要实现数学学习机会的比例平等。从教育资源、人的差异性和社会发展的角度来看，教育不能把人人都培养成数学家，可是国家科学事业的发展又离不开数学家，那么数学学习评价就有义务甄选出有数学才能和兴趣的人进行数学家的教育。需要阐明的是，这两点认识其实并不冲突对立，而是数学教育上的衔接，专家型数学必须生长在大众型数学的基础之上，否则就使数学失去了应有的价值与生命力。

参考文献

[1] 郭元祥.对教育公平问题的理论思考[J].教育研究，2000（3）.

[2] 石中英.教育哲学[M].北京：北京师范大学出版社，2007.

[3] 张良才，李润州.关于教育公平的理论思考[J].教育研究，2002（12）.

[4] 褚宏启、杨海燕.教育公平的原则及其政策含义[J].教育研究，2008（1）.

[5] Anita A.Wager，Noticing Children ParticipationInsights into Teachers toward Equitable Mathematical Pedagogy.Journal for research mathematic education，2007（3）.

[6] Julian Weissglass.Inequity in Mathematics Education：Questions for Educators.The Mathematics Educators，2002（2）.

[7] 史亞娟，华国栋.论差异教学与教育公平[J].教育研究，2007（1）.

[8] 田慧生.活动教育引论[M].北京：教育科学出版社，2000.

[9] 易凌峰.多元教学评价的发展与趋势[J].课程·教材·教法，1999（11）.

[10] 龚玲梅.数学教育评价的回顾与展望[J].数学教育学报，2003（2）.

[11] Indigo Esmonde.Ideas and Identities：Supporting Equity in Cooperative Mathematics Learning.Review of Educational Research，2009（2）.

[作者：汪辉（1986-），男，湖北黄石人，四川职业技术学院助教，硕士。]

【责任编辑 郭振玲】endprint