建模思想在小学数学中的应用

任红君

[摘 要]

要解决一道复杂的数学问题，关键就在于思想方法的运用，而思想方法的核心就是建立模型，它是问题解决的最重要组成部分，体现了学生的学习能力。本文简要提出模型构建的3个重要步骤，并以小学常见的数学类型题为例，通过列举几种基本的数学模型，强调用模型解题的简便性，突出建模思想在小学数学学习中的重要地位。

[关键词]

小学数学；数学建模；模型思想

一、模型的构建

小学的数学问题，多半是数学知识与实际情况相结合产生的。一部分包含生活实际，一部分联系数学专业知识。而数学建模思想就是根据问题中所描述的复杂的已知条件，通过分析问题本质，化繁为简，抽取有用的数学信息，从而把生活情境转化为数学符号或图像，并用数学文字来表示问题的过程。小学学习的数学知识是数学领域最根本的知识，因此在日常数学教学过程中，除了让学生领会课本上的知识以外，教师更应该培养学生的思维方式和解决问题的能力，为以后初中和高中的学习打下坚实的基础。

（一）创设情境，激发兴趣

教师在平时的课堂教学中，可适当地向学生们提出一些他们平时会碰到的问题。比如帮父母卖水果、让学生计算从家到学校的距离、判断东西是否会按时送达等。通过讲述一些身边发生的情况，激发学生兴趣，并逐渐上升到数学问题。通过观察、比较、分析、综合、抽象概括等方式，寻找必要条件，联系已学知识，建立数学模型，形成初步的建模思想观念，通过数学建模，使小学生真正感受到数学知识与外部世界的联系，激发学习兴趣。

（二）找出问题本质，完成模型构建

具体的情境能够激发学生对问题的兴趣，但如果没有将具体情境转化为抽象数学知识，那就无法完成建模。以“圆的认识”为例，如果只是让学生感知象棋、钟表、车轮等具体的生活素材，而忽略寻找它们本质的过程，那么，当学生提取“圆”的模型时，呈现出来的一定是生活中圆形的具体实物，而不是数学意义上的圆。因此，教师在教学过程中，应当注重培养学生找出问题本质的能力。从而建立真正意义上的数学模型，完成从具体到抽象的数学模型的构建过程。

（三）拓展模型，回归生活

从具体情境中构建抽象的数学模型，再将已构建的模型应用到实际生活中，是完整的模型构建的过程。通过将模型还原为具体可感的数学实际问题，使已经构建的模型得到扩充和提升。如经典的“鸡兔同笼”问题模型就是通过研究“鸡”“兔”建立起来的，而这个模型也可以用到许多实际问题中去。例如：自行车与小轿车一共有20辆，它们一共有64个轮子。问自行车有多少辆？小轿车有多少辆？这样通过解答不同的问题，使模型得以拓展和扩充。

二、模型的应用

数学模型，一般来说，就是根据某种事物的特征或数量关系，采用形式化的数学符号和语言，来表示问题的一种特殊的数学结构。在小学数学的学习过程中，许多内容的本质就是数学模型。比如：一年级下册书中讲述过的圆角分的计算，其数学模型实际上就是小数的运算；还有在奥数比赛中经常会遇到的鸡兔同笼问题，其数学模型实质上就是二元一次整数方程。更进一步来说，解决一道数学应用题，就是对一种比较复杂抽象的特定情境用数学符号简化成一个具体的模型。本文根据小学数学应用题的不同类型总结了几种常见的数学模型。

（一）数学文字模型

数学文字型应用题，顾名思义，就是纯文字的一类应用题。这类应用题通常比较复杂抽象，且无關的条件较多。建立文字型数学模型，就是将数学应用题里一些可以忽略的无用条件去掉，将原题改写成只有数学文字表达的模型。经过这样的改变后，应用题的条件和问题都变得一目了然，解题思路也变得清晰许多。举一道小学常见的应用题为例：

例1：小华、小明、小刚三个同学共有45个苹果。如果小华向小明要了三个苹果，然后又送给小刚5个。那么现在三个人拥有的苹果数量恰好相同。问：小华、小明、小刚三个同学原来各拥有多少个苹果？

分析：根据题意，将有用的数学信息抽取出来，用相应的数学文字模型表达。三个同学之间给来给去，没有给别人。那么三个同学拥有的苹果数相同，也就是现在每个同学有45÷3=15（个）。因为小华向小明要了3个苹果后，小明有15个苹果。则原来小明的苹果数为15+3=18（个）。又因为小华给了小刚5个苹果后，小刚有15个苹果，则小刚原来拥有苹果数为15-5=10（个）。则小华拥有的苹果数为45-18-10=17（个）。这样，通过将生活中常见的字眼“要”“送”等转化为数学中的“多”“少”，再进一步简化为“+”“-”，就建立起了简单的数学文字型模型。通过建立模型，使解题变得简单许多。

（二）图式模型

图式这一概念最初是由康德提出的。康德认为图式是“潜藏在人类心灵深处的”一种技术、一种技巧。在小学数学学习过程中，教师应不断地引导学生应用图式模型解决数学问题。建构数学学习图式，有利于找准问题的难点，化繁为简、化难为易；有利于解决数学学习中的困难；有利于学生形成自己独特的知识体系，把脑海中的知识点连成一条线，进而形成自己的知识网络。以一道典型的线段图为例：

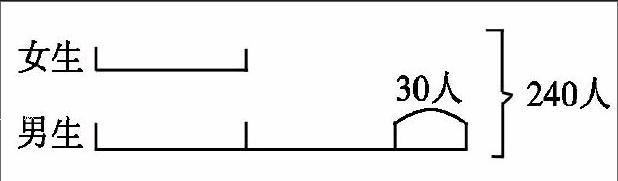
例2：某校五年级学生一共有240人。其中男同学的人数比女同学人数的2倍还多30人。问学校五年级男生有多少人？女生有多少人？

分析：将女同学的总人数看作1份，则男同学的人数是2份+30，由此得到模型

通过线段模型，可以很清楚地看出：女生的人数为（240-30）÷3=70（人）男生的人数为70×2+30=170（人）。

（三）算数模型

算数方法是小学生最先接触的解题方法。在训练学生的独特思维和对数量关系的分析方法上，算数方法是不可替代的。以大家熟悉的问题为例：

例3：在下面空白处填上合适的数。

（1）2，5，8，11， ，17，20……endprint

（2）5，10，15，20， ，30，35……

（3）1，3，4，7， ，18，29……

分析：通过阅读此题，我们能够知道问题中的数与数之间有一种关系。通过观察三个小问题，我们能够直观地看出（1）中后一个数比前一个数大3，容易求得（1）空白处的数字为11+3=14，而14也正好比后一项的数字17小3。在（2）中显然数和数之间不是一种加法关系，第1个数为5×1，第2个数为5×2，通过归纳总结，可以得出第N个数为5×N。所以当N为5时，得出（2）中第5个数为5×5=25。再观察（3），虽然不能直接看出数与数之间的关系，但通过前后数字的作和，可得出这样的关系式：1+3=4，3+4=7，经过总结，我们能够发现数与数之间奇妙的关系，即：前两个数的和等于后一个数。求得空白处的数字为4+7=11。在解决一些问题时，通过建立算数模型，能够很容易找到这些看似杂乱的数字之间的联系。

（四）分类模型

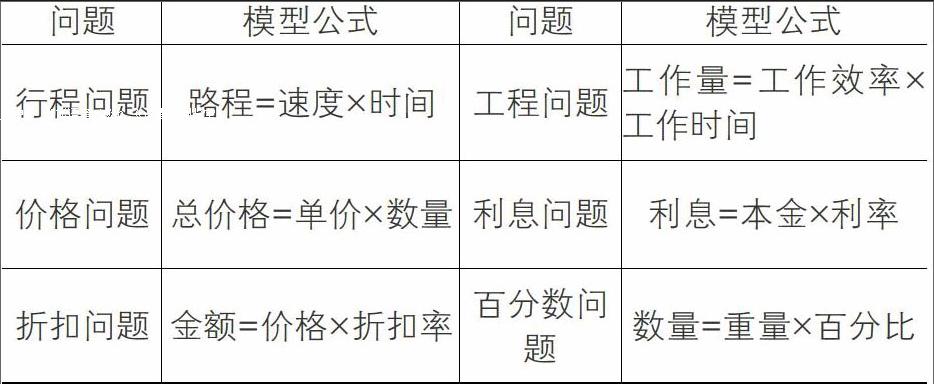
在小學数学教学过程中，教师应积极培养学生的模型意识。使学生在面对复杂问题时，能够第一时间从脑海里找到此类问题所对应的数学模型。小学数学中绝大多数复杂的应用题，我们都可以从中找到一个甚至几个数学模型。也就是说，一些较为复杂的数学模型往往是由几个简单的基础模型组成的。因此，熟练理解并运用基本模型解决问题就变得尤为重要。本文总结了几个在小学数学应用题中常见的基础模型：

三、结语

不同于中学、大学旨在培养数学高素质人才的远大目标，建模思想在小学阶段的应用主要在于培养学生的学习能力、思维能力、学习兴趣，使学生在遇到复杂问题时，能够主动运用建模思想来解决问题、分析问题，形成积极正确的学习态度。《课程标准》曾明确说明：“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。”也就是说，建立数学模型的最基本的目的，就是让学生从数学的角度看待外部世界，理解数学与外界的基本联系。从根本来说，拥有建模意识，可以使学生在分析问题时更接近问题的本质，从而考虑问题更精确、更全面。因此，数学建模思想在小学数学中的应用显得尤为重要。

[参 考 文 献]

[1]姜启源.数学建模[M].北京：北京高等教育出版社，1993.

[2]李罗平.浅谈小学数学建模在数学活动中的运用[J].新课程学习（中），2012（10）.

[3]陈蕾.小学数学建模的三个关注点[J].上海教育科研，2013（8）.endprint