基于FrFT域的雷达压制干扰信号噪声特征提取与分类研究∗

杨 林 王国宏 杨 忠

（海军航空工程学院 烟台 264001）

基于FrFT域的雷达压制干扰信号噪声特征提取与分类研究∗

杨 林 王国宏 杨 忠

（海军航空工程学院 烟台 264001）

针对有源压制干扰条件下干扰类型分类难的问题，提出了一种基于分数阶傅里叶变换域的压制干扰信号特征提取与分类方法。首先，分析了四种典型的压制干扰信号的产生机理；在此基础上，根据分数阶傅里叶变换的性质，对叠加了不同类型压制干扰的线性调频信号进行分数阶傅里叶域分析，并根据分析结果提出压制干扰信号的分类方法；然后对不同干信比下的分类效果进行分析；最后通过仿真实验验证了该方法的有效性，对雷达的压制干扰分类识别具有理论指导意义。

雷达压制干扰；分数阶傅里叶变换；特征提取；方差

C lassNum ber TN95

1 引言

在日益复杂的电磁环境中，现代雷达面临着电子干扰、超低空突防、反辐射攻击等严峻威胁。压制干扰作为雷达干扰的一种主要手段，通过类似于噪声的干扰信号对雷达回波信号进行覆盖，严重影响了雷达作用的正常发挥。因此，如何有效地对抗压制干扰已经成为了雷达抗干扰领域的重要课题［1～3］。对压制干扰类型进行正确识别是开展雷达抗压制干扰研究的前提。目前，国内外相关学者对压制干扰的分类识别方面进行了大量研究。文献［4］基于分数阶傅里叶域的分形特征对压制干扰的存在性进行研究；文献［5］利用分数阶傅里叶对线性调频信号的能量聚集性质，提出了基于分数阶傅里叶变换的雷达抗主瓣压制干扰技术，以上研究主要是针对是否存在压制干扰及如何进行对抗的问题提出了相应的方法。文献［6］提出了一种基于分数阶傅里叶变换和分层决策分类算法的宽带干扰自动识别方法；文献［7］引入了特征加权和相像系数聚类算法，对雷达有源压制干扰进行了分类识别，以上研究对于压制干扰识别特征的提取提出了几种思路，但在识别的准确率和分类的精细程度等方面还有待进一步提高。针对上述问题，本文针对几种典型的压制干扰信号，提出了一种基于分数阶傅里叶变换的方差和匹配阶数的特征提取方法，并在不同的干信比条件下进行仿真验证，得出的结论对于雷达压制干扰分类识别具有一定的参考价值。

2 典型压制干扰信号模型

雷达是通过接收回波信号并与发射信号进行对比关联从而发现目标并对其参数进行测量的。任何雷达都有内部噪声或外部噪声，压制干扰就是通过产生并发射与噪声类似的干扰信号进入接收机，对有用的回波信号进行覆盖或压制。当干扰功率足够强时，就会导致雷达接收机的输出信噪比急剧恶化，从而给雷达检测发现目标造成困难。根据干扰噪声调制方式和数学模型的不同，压制干扰信号可以分为射频噪声干扰、噪声调频干扰、噪声调幅干扰、噪声调相干扰。其数学模型可以分别表示为

射频噪声干扰：

式中，包络Un(t)服从瑞利分布，相位ϕ(t)与Un(t)相互独立，并且在[0，2π)内服从均匀分布。ωj为载频，远大于J(t)的谱宽。

噪声调频干扰：

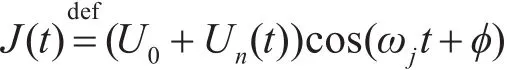
式中，调制噪声Un(t)的均值为零，其方差等于σ2n并且是分布在[-U0，∞)的广义平稳随机过程；U0、ωj为常数；ϕ是均匀分布在[0，2π)上的随机变量，并与Un(t)相互独立。

噪声调相干扰：

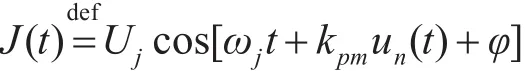
式中，Uj、ωj为常数，分别表示噪声调相干扰信号的振幅及中心频率；kpm为常数，称为调相系数；式中，调制噪声u(t)是零均值的广义平稳随机过程；ϕ为在[0，2π)上均匀分布的随机变量，并且与u(t)相互独立；Uj、ωj、KFM为常数，分别是噪声调幅干扰的振幅、中心频率和调频斜率。

噪声调幅干扰：un(t)为调制噪声；φ为随机变量，并在[0，2π)区间内呈均匀分布，且与ut(t)相互独立。

3 基于分数阶傅里叶变换的压制干扰信号特征提取

分数阶傅里叶变换是在统一的时频域上对信号进行处理，是传统傅里叶变换的广义形式。与傅里叶变换相比，分数阶傅里叶变换在处理非平稳信号方面有着更明显的优势，且处理起来更加灵活，因此广泛应用于信号处理领域。

定义x(t)为t域内的信号函数，那么从积分变换的角度，x(t)的分数阶傅里叶变换为

式中，α=pπ/2，p表示分数阶傅里叶变换的阶数，Fp称为 p阶傅里叶变换算子。

线性调频信号（LFM信号）是指频率随时间而线性改变的信号，其在雷达的应用中非常广泛，因此考虑雷达信号为LFM信号时受到压制干扰的情况。定义线性调频信号为

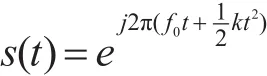
其频率与时间满足 f(t)=f0+kt。其中，f0为零时刻的频率，k为调频斜率。

当雷达受到压制干扰时，接收到的回波信号模型为

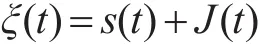
式中，s(t)为有用的目标信号，J(t)为压制干扰信号，其数学模型可能为上文提到的四种典型压制干扰信号中的一种。下面将具体分析在分数阶傅里叶域内压制干扰信号对于信号能量分布产生的影响。

根据分数阶傅里叶变换的性质，LFM信号在分数阶傅里叶域内的相应位置会产生能量聚集现象，随着α角度的扫描，会有一个合适的角度，使得线性调频信号呈现出高度的能量聚集性；而压制干扰信号通常是随机分布的，与目标信号不存在相关性，其中，高斯白噪声在分数阶傅里叶域内的能量是均匀分布的，能量并不会发生聚集；而经过调制的干扰噪声信号也只会在某一阶次或者局部出现很弱的聚集。图1为不同类型的压制干扰信号在分数阶傅里叶域内呈现的能量分布情况，可以看出，调制噪声在某些点存在能量较小的尖峰。

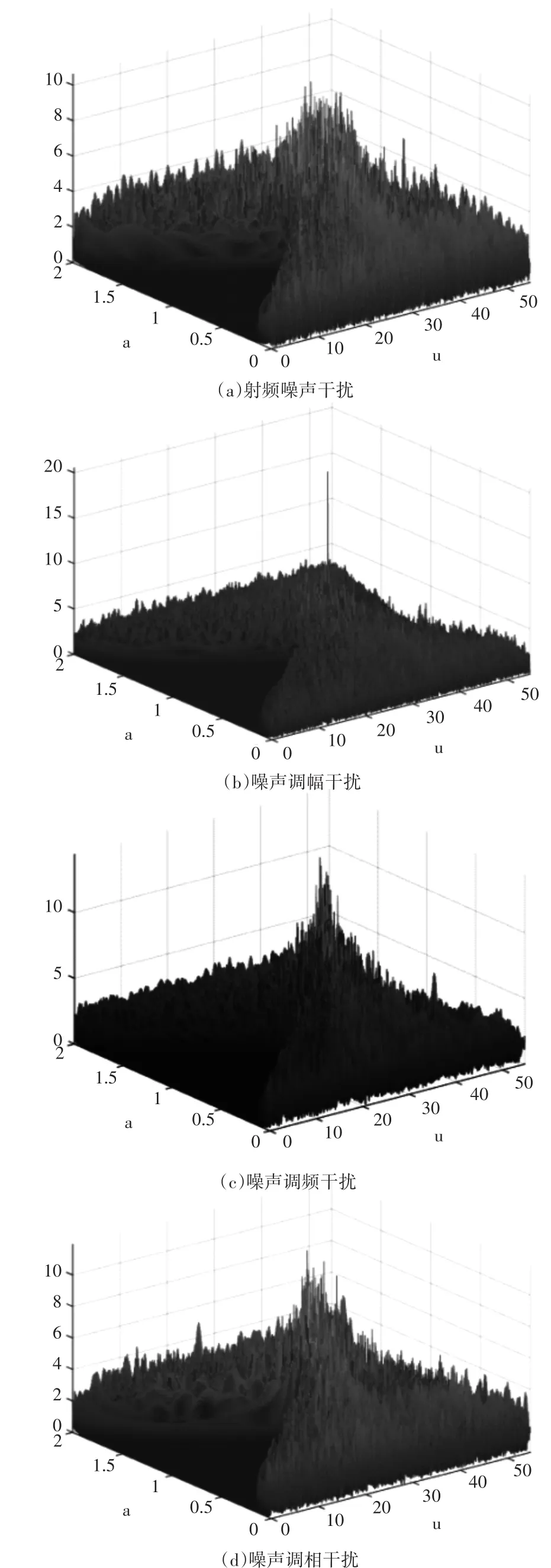
图1 不同类型压制干扰信号FrFT域能量分布

根据上述分数阶傅里叶变换的特性，我们考虑将受到压制干扰的信号ξ(t)在分数阶傅里叶域内进行分析，以旋转角α为变量进行扫描。此时我们可以得到信号能量在(α，u)平面上的二维分布，在此基础上对该平面的峰值点进行搜索即可检测出LFM信号，此时根据α=pπ/2计算得出的阶数 p称为匹配阶数。该过程可以描述为

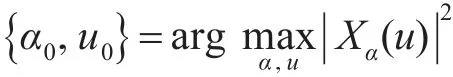
LFM信号的参数可以估计为

为获得更好的压制干扰效果，压制干扰信号通常会进行调制，同时干扰的功率一般远大于信号的功率。此时对ξ(t)进行分数阶傅里叶变换，其结果呈现出的能量聚集性必然会受到强干扰信号的影响，即除了线性调频信号呈现出的能量聚集性之外，信号能量还会在其它局部位置会发生随机起伏。同时LFM信号的检测和参数估计也会出现误差。上文提到的四种典型的压制干扰信号是通过不同方式进行调制的，它们对于分数阶傅里叶域能量聚集性的影响也是不同的。下面将基于不同压制干扰信号对分数阶傅里叶域能量聚集性的影响提取识别特征。

在统计学中，方差可以用来衡量一组数据的离散程度，即每个样本值与全体样本值均值之差的平均数。对于受到压制干扰的信号ξ(t)，我们可以分以下几个步骤进行特征提取：

首先，进行功率归一化处理。考虑到当雷达受到压制干扰时，信号ξ(t)的功率一般是未知的，为了避免功率变化对特征值的影响，因此先将功率进行归一化后再进行处理。具体做法是首先计算信号ξ(t)的功率Pξ，根据信号功率和幅度大小的关系，可以得到功率归一化后的信号为

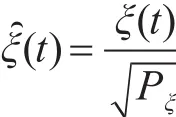
然后，对功率经过归一化的信号(t)进行分数阶傅里叶变换，得到在(α，u)平面上二维分布的Xα(u)，即

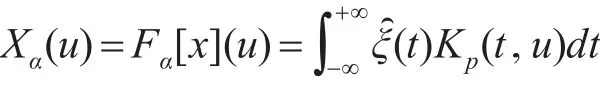
最后，计算平面(α，u)内所有的信号能量的方差。信号能量的均值为其表达式为

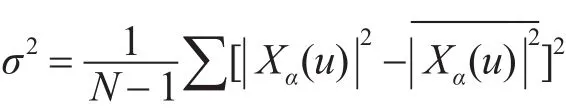
经过以上步骤求得的方差σ2，可作为压制干扰的识别特征。通过预先设定的阈值就可以对压制干扰样式进行分类识别。

4 仿真验证

4.1 仿真条件

设线性调频信号的时宽为10μs，带宽为60MHz，调频斜率k为6000GHz/s；射频噪声干扰是由高斯白噪声通过截止频率为60MHz的滤波器得到；噪声调频干扰中心频率为30MHz，调制噪声截止频率为20MHz，噪声调频斜率kfm为30MHz/V；噪声调幅干扰中心频率为30MHz，调制噪声截止频率为20MHz，有效调制系数取10；噪声调相干扰中心频率为30MHz，调制噪声截止频率为20MHz，调相斜率kpm取6；采样频率取300MHz。

4.2 仿真结果

通过500次蒙特卡洛仿真实验，得到干信比不同时特征值σ2的变化情况。取干信比变换范围为30dB～40dB时，如图2所示。

图2 不同干信比条件下σ2结果

由图2可以看出，当干信比发生变化时，尤其是干信比较高时（大于20dB），提取的特征值σ2对不同干扰样式的区分效果比较明显。同时，在干信比较高时，提取的特征值σ2的变化幅度也比较平稳，只在很小的范围内波动，这也有利于特征值门限的选取。

根据上述实验获得的数据，可以提取不同类型压制干扰的特征值的经验值范围。具体得到的特征值阈值如表1所示。

表1 压制干扰信号特征值阈值

根据仿真得到的结果，进一步将压制干扰信号分类识别模型修正如下：

1）若σ2＜3.8，则压制干扰类型可能为射频噪声干扰；

2）若 3.8＜σ2＜3.95，则压制干扰类型可能为噪声调相干扰；

3）若3.95＜σ2＜4.1，则压制干扰类型可能为噪声调幅干扰；

4）若σ2＞4.1，则压制干扰类型可能为噪声调频干扰。

4.3 不同干信比条件下特征值σ2检测性能仿真

为验证上述分类识别方法的识别性能，下面将进行仿真实验。设目标信号为线性调频信号，其参数同上。分别对雷达受到射频噪声干扰、噪声调幅干扰、噪声调频干扰、噪声调相干扰这四种情况进行仿真模拟。压制干扰干信比设置为从30dB步进至40dB，识别门限选取表1中的结果。经过500次蒙特卡洛仿真实验，得到对不同压制干扰类型的识别正确率曲线如图3所示。

4.4 仿真结果分析

本节通过仿真实验，给出了压制干扰分类识别门限，并得到了该方法对于不同压制干扰信号的分类识别概率曲线。从仿真结果来看，可以得到以下结论：

1）在不同类型的压制干扰信号的影响下，目标信号在分数阶傅里叶域内的能量聚集性会受到不同程度的影响。不同压制干扰信号所产生的影响主要表现在信号能量离散程度的不同。因此可以选取方差σ2作为识别特征。

2）特征值σ2的大小只与压制干扰类型有关。在干扰强度较低的情况下（干信比小于20dB），特征值σ2对干扰类别的分类效果并不明显，这是由于信号的存在可能会对特征值的大小产生一定的影响；而当干扰强度较强时（干信比大于30dB），特征值σ2则具有明显的分类效果，此时信号强度已经非常微弱，对特征值σ2的影响已经可以忽略。

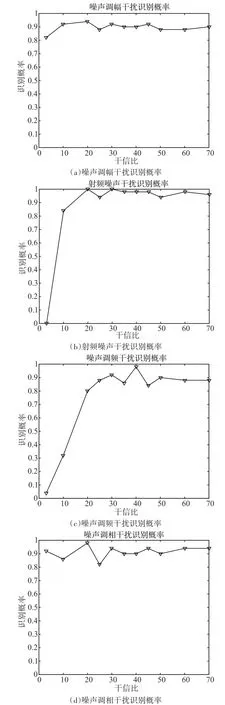
图3 不同压制干扰类型识别率

3）通过仿真验证表明，在压制干扰强度较强（大于20dB）时，识别准确率基本能达到90%以上，对于压制干扰类型具有较高的识别率。其中，该方法对于噪声调幅干扰和噪声调相干扰具有较好的识别性能，在干信比较低（小于10dB）时仍能有效识别干扰类型。出现的差错主要集中在干信比较低时对射频噪声干扰和噪声调频干扰的识别上。尤其是对于噪声调频干扰，必须保证有较高的干信比（大于30dB）才能对其进行有效的识别。

5 结语

本文针对雷达压制干扰分类识别的问题，根据四种典型的压制干扰信号模型，从原理上分析了利用分数阶傅里叶变换进行压制噪声特征提取的可行性，给出了相应方法，通过仿真分析给出了相应的判决门限，并通过仿真实验，验证了不同干信比条件下特征值的识别效果。结果表明，该方法在干信比较高的情况（大于30dB）下对于压制干扰信号具有较好的分类识别效果，整体的识别概率能达到90%以上。尤其对于噪声调幅干扰和噪声调频干扰，该方法在干信比小于10dB时仍然能维持80%的识别概率，具有较好的识别性能。出现的差错主要集中于在干信比较低（小于20dB）时对噪声调频干扰和射频噪声干扰的识别上。尤其对噪声调频干扰，该方法需要干信比达到30dB才能保证较高的识别概率。因此，如何在干信比较低的情况下有效地识别射频噪声干扰和噪声调频干扰需要对该方法进行进一步完善和改进。

［1］赵国庆.雷达对抗原理［M］.2版.西安：西安电子科技大学出版社，2012：122-143.

［2］杜辉.电子战综述［J］.计算机与网络，2005（7）：50-52.

［3］周一宇，安玮，郭福成.电子对抗原理［M］.北京：电子工业出版社，2009：73-85.

［4］祝宏，江舸，张海，唐高弟，李中云，等.基于FRFT域分形特征的压制干扰存在性检测［J］.强激光与粒子束，2016，28（5）：1-7.

［5］王文涛，张剑云，曹磊，王瑜，等.FRFT应用于雷达抗主瓣压制干扰技术研究［J］. 现代防御技术，2015，43（6）：183-189.

［6］陈自力，韦乃棋，朱安石，等.基于分数阶Fourier变换的宽带干扰识别方法［J］.光电与控制，2013，20（10）：102-105.

［7］李广强，贺奎，张良，唐翥，等.基于特征加权与相像系数聚类的有源压制干扰分类技术［J］.舰船电子对抗，2014，37（6）：26-28.

［8］鲍晓利，冯永新.宽带扫频式干扰的仿真与FPGA实现［J］.沈阳理工大学学报，2008，27（3）：61-64.

［9］何友，修建娟，张晶炜，等.雷达数据处理及应用［M］.北京电子工业出版社，2006：165-169.

［10］陶然，王越，邓兵，等.分数阶Fourier变换在信号处理领域的研究进展［J］.中国科学 E 辑，2006，49（11）：1-25.

［11］孙即祥.现代模式识别［M］.长沙：国防科技大学出版社，2001：9-18.

［12］POISEL R.Modern communications jamming principlesand techniques［M］.2nd ed． London：Artech House Press，2011：9-18.

［13］王党卫，秦江敏，马晓岩，等.基于模式分类检测的射频噪声干扰抑制方法［J］.空军雷达学院学报，2003，17（1）：4-6.

［14］徐会法，刘峰.线性调频信号分数阶频谱特征分析［J］.信号处理，2010，26（12）：1896-1901.

［15］齐林，陶然，周思永，等.基于分数阶傅里叶变换的线性调频信号的自适应时频滤波［J］.兵工学报，2003，24（4）：499-503.

Research on Noise Feature Extraction and C lassification of Radar Suppression Interference Signals Based on FrFT Domain

YANG Lin WANG Guohong YANG Zhong
（Naval Aeronautical Engineering Institute，Yantai 264001）

Aiming at the problem of classification of interference type under active suppression interference condition，a feature extraction and classificationmethod of suppression interference signal based on fractional Fourier transform domain is proposed.Firstly，the generationmechanism of four typical suppression interference signals is analyzed.On this basis，the fractional Fourier transform of the LFMsignalswith different types ofsuppression interference is carried outaccording to the nature of fractional Fourier transform.Finally，the validity of themethod is verified by the simulation experiment，which is of theoretical significance to the classification and recognition of the suppression of the radar.In this paper，the classification of the jamming signal isanalyzed.

radar suppression interference，fractional fourier transform，feature extraction，variance

TN95

10.3969/j.issn.1672-9730.2017.09.012

2017年3月10日，

2017年4月24日

杨林，男，硕士研究生，研究方向：雷达抗干扰技术。王国宏，男，教授，博士生导师，研究方向：多源信息融合、雷达组网、目标检测与跟踪等。杨忠，男，博士研究生，研究方向：多传感器信息融合、雷达抗干扰技术。