交易量影响波动率的成因：交易规模还是交易次数？

马长峰，陈志娟

(浙江工商大学 金融学院，浙江 杭州 310018)

交易量影响波动率的成因：交易规模还是交易次数？

马长峰，陈志娟

(浙江工商大学 金融学院，浙江 杭州 310018)

文章基于2001-2016年间日度数据，首先验证了沪深两市个股和指数都存在交易量和波动率之间的正相关。将交易量分解为交易规模和交易次数，发现中国A股市场上交易规模和交易次数各自对波动率具有解释能力。交易规模和交易次数同时作为解释变量时，虽然交易规模在2009年前子样本对波动率不具解释能力，但是2009年后子样本和全样本中对波动率具有解释能力。考虑价格冲击之后，交易次数在全样本和两个子样本中对波动率都具有解释能力，说明中国市场上交易规模和交易次数对波动率的解释能力是并存的。进而证明了交易量和波动率之间的正相关在金融危机期间和平时并无显著差异。

交易量；波动率；交易规模；交易次数；金融危机

一、 引 言

本文分析中国上海证券交易所和深圳证券交易所两个市场的股票波动率能否被交易量解释。股票波动率作为或有要求权定价、风险管理、资产配置和市场有效性检验的基石，是金融学的核心变量，因此学术界对此进行了广泛而深入的研究。Engle (1982)[1]提出了刻画金融市场波动丛集性的ARCH模型，*GARCH类模型的文献很丰富，例如朱钧钧和谢识予 (2011)[2]运用MCMC方法估计了上证综指的MS-TGARCH模型证明上证综指波动率具有双重不对称性，张宗新和王海亮 (2013)[3]将波动率归因于信念和情绪，郑挺国和尚玉皇 (2014)[4]基于宏观基本面利用GARCH-MIDAS模型改进日度波动率估计。虽然深刻揭示了波动率的丛集性，但ARCH类模型主要刻画条件方差，对于无条件方差的解释以及波动率的成因则缺乏理论阐述。在波动率的成因方面，由于French和Roll (1986)[5]等发现波动率并不能由基本价值的变化完全解释，因而学术界转而探索投资者交易行为能否解释波动率，因此交易量能否解释波动率(交易量-波动率相关性)就成为一个重要的研究领域。这个领域的基础是信息不对称、意见分歧等对于资产价格变化的解释，因此对于资产定价的理论分析具有重要意义，也出现了大量的实证研究。

虽然交易量能否解释波动率已经出现了大量研究，但是本文研究具有的重要意义在于：第一，学术界对于波动率的理论解释尚无定论，例如Adam等(2016)[6]仍然在理论上寻求对于波动率的解释，因此探索波动率的成因具有重要意义。第二，交易量对于波动率的解释目前尚未定论，仍有大量研究集中于此，例如Bollerslev等 (2016)[7]仍然在探讨交易量对于波动率的解释，Rannou和 Barneto (2016)[8]对欧洲碳排放市场的波动率和交易量之间的相关性进行了经验分析。第三，作为最大的新兴市场，中国A股市场已经确定将于2018年被纳入MSCI指数，届时必将成为世界金融市场的重要组成部分从而受到世界各大机构投资者的关注和参与，而中国A股市场波动率的解释却十分欠缺。因此，本文从交易量的角度分析中国A股波动率的成因，具有重要的学术价值。最后，寻求波动率的解释因素对于中国监管部门也具有实际意义。

本文研究的贡献有如下四点：第一，证明了最大的新兴市场——中国A股市场存在稳健的交易量与波动率正相关性，拓展了这一问题的研究范围；第二，本文证明在一个纯粹的指令驱动市场上也存在交易量和波动率的正相关性，为资产价格变化理论分析提供了新的证据。报价驱动市场上交易量受到做市商存货的影响，而指令驱动市场上交易量受到委托指令簿的深度的影响，也就导致交易量和波动率的相关程度不同。同时，Chan和 Fong (2000)[9]认为微观结构的差异会导致交易规模和波动率之间关系的变化。由于纯粹通过计算机控制的委托指令簿撮合交易，中国A股市场的交易机制与NYSE和NASDAQ市场交易机制显著不同，因此本文的研究为交易量与波动率相关性及其相关的资产价格变化理论模型提供了更多事实依据。第三，本文发现中国A股市场上交易规模和交易次数对波动率的解释力并存，为投资者交易行为导致资产价格变化的理论分析中将交易规模内生化提供了经验证据。第四，本文证明交易量和波动率之间的正相关在金融危机期间和平时并无显著差异。

本文其他部分结构如下：第二部分是相关文献回顾和理论假设；第三部分是样本、变量和描述性统计量；第四部分是实证研究结果报告；第五部分是全文总结。

二、 文献回顾和理论假设

投资者交易对波动率的解释可以按照是否区分投资者类型分为两类，第一类区分投资者类型，第二类不加区分。第一类文献中最重要的是机构投资者交易对于波动率的影响。*Foucault等(2011)[10]发现个人投资者交易增加波动率。国内学者对于机构投资者交易能否降低波动率存在争议：祁斌等 (2008)[11]、林忠国和韩立岩 (2011)[12]、谭松涛等 (2014)[13]对此持正面观点，即认为机构投资者能够降低波动率；与此相反，蔡庆丰和宋友勇 (2010)[14]却认为机构投资者增加了波动率，史永东和王谨乐 (2014)[15]也发现机构投资者对波动率的影响随着市场上升和下降而变化。

与特定类型投资者对波动率的影响不同，本文主要是分析总体交易量和波动率之间的关系。在中国A股交易量与波动率相关性研究方面，以往的研究主要是以GARCH模型为基础。*采用GARCH模型研究成交量和波动率的经典文献是Lamoureux和 Lastrapes (1990)[16]。赵留彦和王一鸣 (2003)[17]采用GARCH模型研究交易量和指数波动率的相关性，这与本文以个股作为研究对象显著不同。王燕辉、王凯涛 (2004)[18]和杨炘、王邦宜 (2005)[19]同样采用GARCH模型，虽然以个股作为分析对象，但都是仅以20只股票为样本分析交易量对于波动率持续性的解释，因此样本数量偏小。上述文献都是以GARCH模型为基础探讨交易量和波动率的关系，其特征表现为：第一，GARCH模型侧重波动率丛集性的描述，而非波动率的成因；第二，样本期都比较短，而且包含的个股偏少，因此难以避免样本偏差。

尽管国内相关研究匮乏，国际上交易量和波动率之间的相关性以信息不对称和意见分歧等理论模型为基础，是一个很重要的研究方向，在长达几十年的时间里持续被学术界关注和研究。在实证研究方面，学术界发现这一现象存在于股票、期货和汇率市场，存在于小时、日度、周度等不同频率，是一个普遍存在的规律。为了解释这一现象，学术界发展了三种理论模型。第一种是以Tauchen和 Pitts (1983)[20]等文献为代表的混合分布模型。该理论假设收益率和交易量都是以某个时间间隔(例如一天)内到达金融市场的信息数量(混合变量)作为条件的正态分布，各自均值和标准差都与混合变量成正比，相互之间的条件协方差为零。收益率和交易量之间的无条件联合分布就是条件正态分布的混合，而条件正态分布都以混合变量作为条件，因此解释了交易量和波动率之间的相关性。第二种是以Kyle (1985)[21]以及Admati和Pfleiderer (1988)[22]为代表的信息不对称模型。这种模型认为信息交易者提交的指令对应的交易量反应了其私有信息，因此信息交易者交易量增加就会使价格体现更多信息从而增加波动率，因此交易量和波动率正相关。第三种是以Scheinkman和Xiong (2003)[23]以及Banerjee和 Kremer(2010)[24]为代表的意见分歧模型。意见分歧模型认为，当公共信息由好变坏(反之亦然)，投资者的异质信念会引起交易(量)，而公共信息同时影响价格和交易量，因此就导致了交易量和波动率的正相关。

在与本文更为相关的研究中，陈梦根和毛小元 (2007)[25]虽然也分析了波动率和换手率之间的关系，但是该文与本文至少有三点不同：第一，交易量的度量指标不同，在交易量与波动率相关性检验的文献中一般采用成交股数而不是换手率度量交易量；第二，该文并非以交易量与波动率相关性检验为主要研究对象；第三，该文以换手率而不是波动率作为被解释变量，并未控制波动率的滞后项，这样该文得到的换手率和波动率正相关的结论就需要进一步验证。另外，唐齐鸣和刘亚清 (2008)[26]采用SVAR模型分析A股和B股之间(内部)的信息传递，也分析了成交量和波动率之间的关系，但是该文研究对象限于指数，这与本文以个股分析为主是截然不同的。

综上所述，中国A股市场作为最大的新兴市场，其交易量与波动率之间的正相关关系有待验证。更重要的是，交易规模是否影响波动率存在争议：虽然Chan和 Fong (2000)[9]认为交易规模对波动率有影响，但是Jones等(1994)[27]却发现交易次数包含了几乎所有信息从而导致交易规模失去对波动率的解释力。交易规模与价格冲击和信息有关。个人投资者限于资金水平而极少提交大单，正因如此，平均单笔交易量也就是交易规模能够体现提交大单的机构投资者的交易。一般认为机构投资者是知情交易者，那么根据信息不对称模型，交易会将其信息展现出来[28-29]，而这伴随着价格变化，也就会导致交易规模和波动率的正相关。

如果机构投资者拆单隐藏交易动机，则其最优策略是提交中等规模的交易指令，则交易规模和波动率之间就不会正相关，然而，有两个原因使得这个结论在中国A股市场不成立。第一，信息的时效性要求机构投资者尽快使用其私有信息，因此机构投资者很可能不会过度依赖拆单。第二，个人投资者的交易非常活跃使得中国A股市场流动性非常充沛，因此机构投资者无需依赖拆单。所以，我们预期交易规模与波动率存在正相关。由于交易规模越大，价格冲击越大，因此我们预期价格冲击会影响交易规模和波动率之间的相关性。

交易次数对应交易频率，这在一定程度上体现了流动性，例如Lippman和 Mccall (1986)[30]就将成交所需时间长度定义为流动性，因此某一周期(例如一日)内的交易次数就是流动性的一种度量。从这种角度来说，交易次数越多表明流动性越好，因此越不容易产生价格冲击，也就会降低价格波动。另一方面，交易次数越多体现了噪音越大，因此会增加价格波动率。而在中国A 股市场上，个人投资者是绝对多数，而我们预期交易次数主要体现噪音，会增加波动率。

三、 样本、波动率度量和描述性统计

本文的样本来自锐思股票数据库的2001-2016年间所有沪深两市非ST个股日度数据，包括收益率、流通市值、最高价、最低价、交易量(股数)、交易笔数等。交易量单位取为10万股/天，交易笔数是100次/天。

本文以极差波动率作为股票i在日期t的波动率的度量，具体定义如下：

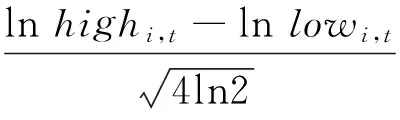
(1)

其中highi,t和lowi,t分别表示股票i在t日的最高价和最低价。根据Alizadeh等(2002)[31]的研究结果，该波动率指标不仅是有效的，而且对于微观结构噪音是稳健的。为了保证结论的稳健性，我们也采用文献中惯用的另一种指标来度量波动率，即经过(2)式回归得到的收益率残差的绝对值|εi,t|(以下称残差波动率)：

(2)

其中Ri,t表示股票i在日期t的收益率，Dk,t表示周一到周五的虚拟变量(D1,t在周一取1，否则取0，其余以此类推)。Schwert (1990)[32]提出将(2)式中的残差绝对值作为波动率的估计值，之后这一方法成为波动率文献中广为使用的方法，例如Avramov等 (2006)[33]、Chan和Fong (2000)[9]、Jones等 (1994)[27]都采用了这一度量方法。

由于面板数据既有横截面又有时间序列，仅仅矫正其中一个维度的相关性并不充分，因此Thompson (2011)[34]和Cameron等 (2011)[35]给出了一种同时矫正时间序列和横截面相关性的方法。为了得到稳健的结论，本文对于个股的分析采用二维丛集性(two-way clustering)矫正标准误，指数的分析采用Newey和West (1987)[36]矫正标准误计算t统计量。

表1给出了本文关键变量的描述性统计量。每年按照流通市值将所有股票动态分为5组，然后计算每个市值组合中各个变量的均值、中位数、标准差、峰度和偏度等统计量，同时给出所有股票的相应统计量。表中极差波动率的均值、中位数和标准差并未随着市值而单调变化，说明平均而言市值差异并未伴随着波动率差异。峰度和偏度却随着市值而变化较大，说明不同市值组合的波动率的分布并不相同。最小市值组合的波动率均值明显偏大，说明小市值股票的波动率相比其他市值组合较大。

交易量指的是每日个股的交易股数，其均值、中位数都随市值单调递增，表明大市值股票比小市值股票交易更活跃。交易量随着市值变化非常明显，意味着实证分析应该按市值分组进行。最大市值组合的交易量显著高于其他组，为分组分析提供了更强的依据。交易规模等于交易量和交易笔数的比值，表1显示平均一笔成交1400股，也就是14手。不同市值组合之间的交易规模相差并不大，但是中等股票的交易规模的偏度和峰度显著不同于其他市值组，说明中等市值的股票的交易规模分布显著异于大市值股票和小市值股票。交易次数虽然并不随市值单调变化，但是最大市值组的交易笔数显著高于其他市值组合，而且其峰度和偏度也显著高于其他组，这也是后续分析采用市值分组的根据。平均而言，一只股票每天成交5580笔，平均每分钟成交超过23笔，说明交易非常活跃。最大市值的股票交易最频繁，但交易最不频繁的并非小市值股票而是中等市值的股票。

表1 描述性统计量

四、 实证研究结果及分析

这一部分中，首先验证中国A股市场是否存在交易量和波动率的正相关。中国和美国分别代表了最大的新兴市场和最大的发达市场，而且A股是纯粹的电子指令驱动市场，因此验证A股市场是否存在交易量和波动率的正相关的意义在于将这个结论适用的范围从发达市场拓展到新兴市场，从有人工参与的撮合交易拓展到全无人工参与的撮合交易。然后我们着重分析交易规模、交易次数对波动率的解释。

(一) 交易量波动率正相关的验证

1.交易量(股数)波动率相关性检验。为了检验交易量波动率之间的相关性，参考Chan和Fong (2000)[9]等文献，每年对每只股票进行如下回归：

(3)

式(3)中σi,t表示股票i在日期t的波动率，用极差波动率度量；vlmi,t表示交易量(单位是10万股)的对数；MDt表示周一虚拟变量(周一取1，否则取0)。由于波动率具有丛集性，因此在式(3)中包含12阶波动率滞后项作为控制变量。为了分析回归结果是否随市值而变化，每年按照第一个交易日的流通市值将股票分为5个市值组合。并且要求每年进入样本期的股票至少具有60个观测。表2中分别对所有股票以及5个市值组合报告式(3)系数估计值的平均值，同时圆括号中给出经过横截面(同一年不同股票之间)和时间序列(同一股票)二维丛集性矫正的t统计量。为了节省篇幅，表2省略掉12阶波动率滞后项的系数估计结果。为了显示结论的稳健性，除了A栏的全样本结果，表2的B栏和C栏给出了2009年前后两个子样本的估计结果。

表2的A栏中αiM所在的行是周一虚拟变量的系数估计值及其t统计量，最后一列显示所有股票的αiM估计值为0.0011，对应t统计量是4.78，在1%水平上显著，说明极差波动率在周一显著高于其他工作日，因此中国A股市场存在波动率的周一效应。5个市值组合的αiM估计值同样在1%水平上显著为正且差异很小，说明周一效应显著且不受市值影响。表2的 A栏中最后两行是交易量系数估计值及其t统计量，最后一列显示所有股票的交易量系数的估计值为0.0082，对应t统计量为13.66，在1%水平上显著为正，说明交易量和波动率显著正相关。5个市值组合的交易量系数估计值也都是在1%水平显著为正，但并不随着市值而单调变化，说明交易量和波动率之间的强正相关并不受市值的影响。这与美国市场发现的交易量和波动率正相关是一致的。

表2的B栏给出了2009年前这一子样本的交易量波动率相关性检验结果，为了节省篇幅，我们只报告交易量系数的估计值和t统计量。最后一列显示在2009年前子样本中，所有股票的交易量系数估计值显著为正，而且这种显著为正同样存在于不同市值组合中。表2的C栏显示2009年后这一子样本的交易量系数估计值不论是在全部股票还是5个市值组合中都显著为正，表明交易量和波动率之间的正相关性同样存在于这一子样本中。表2说明，中国A股存在稳健的交易量和波动率之间的强烈的正相关性。对比2009年前后两个子样本，不难发现，交易量系数的估计值由2009年前的0.0071增加至2009年后的0.0093，对应的t统计量由8.69增加至12.33，意味着这种正相关随着时间推移而增强。

表2 个股交易量波动率相关性检验

注:*、**、***分别表示估计值在10%、5%和1%水平下显著。

2.指数交易量和波动率相关性分析。选取有代表性的上证指数、A股指数和沪深300指数，利用式(3)估计这三个指数交易量和波动率之间的相关性，结果如表3所示。对于指数不需要考虑残差的横截面相关性，因此分别对每个指数进行GMM估计从而对标准误采用Newey-West矫正序列相关。为了节省篇幅，表3仅仅给出了三个指数交易量估计值及其经过Newey-West矫正的t统计量(在圆括号中)，同时给出全样本以及2009年前后两个子样本结果。表3中第三列显示上证指数、A股指数和沪深300指数在全样本期间交易量系数的估计值分别是0.5311，0.4849和1.0791，都在1%水平显著，证明指数交易量和波动率之间同样存在显著为正的相关性，即指数交易量的增加伴随着波动率的增加。表3第四列和第五列显示上证指数、A股指数和沪深300指数在2009年前后两个子样本中交易量系数估计值都在1%水平显著，同时这三个指数交易量和波动率之间的正相关表现出增强的趋势。综合表3关于指数的结果和表2关于个股的结果，表明交易量和波动率之间的正相关关系不仅存在于中国A股市场的个股，同样存在于指数，且表现出增强的趋势。验证了交易量和波动率之间的显著正相关性之后，下面继续探讨这种正相关是来自交易规模还是交易次数。

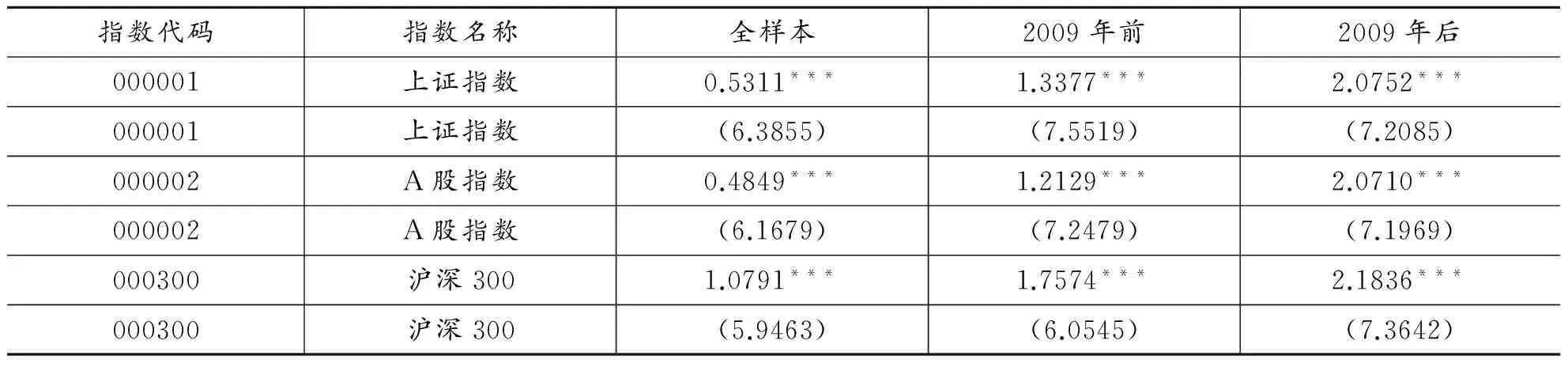
表3 指数交易量波动率相关性检验

注:*、**、***分别表示估计值在10%、5%和1%水平下显著。

(二) 交易量影响波动率的成因来自交易规模还是交易次数？

1.交易规模波动率相关性检验。交易量可以进一步分解，将交易量除以交易次数，即得平均每次成交的交易量，也就是交易规模。Grundy和Mcnichols (1989)[37]、Holthausen和Verrecchia (1990)[38]、Kim和Verrecchia (1991)[39]等文献认为交易规模含有价格信息，因此交易规模可能影响波动率。为了检验交易规模和波动率之间的相关性，每年对每只股票进行如下回归：

(4)

式(4)将式(3)中的交易量vlm换做交易规模AV，其余变量含义保持不变。表4的A、B和C栏分别给出了全样本、2009年前子样本和2009年后子样本中交易规模和波动率相关性检验的结果，每一栏结果都分为全部股票以及5个市值组合。A栏中间两行的最后一列显示全部股票估计得到的周一虚拟变量的系数估计值为0.0013，在1%水平上显著，同样证明A股日度波动率具有周一效应。5个市值组合的结果表明周一效应不随市值而发生变化。A栏最后两行是交易规模的系数估计结果，最后一列显示全部股票估计得到的交易规模的系数估计值为0.4978，在1%水平上显著，表明平均单笔成交的交易量越大，伴随着波动率越高。5个市值组合同样给出了显著为正的交易规模系数估计值，且全部在1%水平上显著，表明交易规模和波动率的正相关存在于所有市值组合当中。比较5个市值组合，发现交易规模系数的估计值随着市值增大而单调减小，表明市值越大，交易规模对于波动率的解释能力越弱。最小市值组合的交易规模系数估计值和t统计量都明显高于其他组合，表明交易规模对于波动率的影响在小市值股票中特别明显。

表4的B栏给出了2009年前这一子样本的交易规模的估计值，同样显示交易规模和波动率之间显著的正相关不仅存在于全部股票，而且存在于不同的市值组合当中，表明交易规模和波动率之间的正相关是稳健的。同时，随着市值的增加，交易规模的系数估计值单调递减，表明在2009年前这段时期内，市值越小交易规模对于波动率的影响越大，这与A栏中全样本的结果是一致的。

表4的C栏给出了2009年后这一子样本的交易规模的估计值，结果显示全部股票的交易规模和波动率之间显著正相关，然而5个市值组合的结果与全样本和2009年前的子样本却有不同之处。一是第3组的估计值仅在5%水平上显著，尽管其他组仍然是1%水平上显著。二是估计值不再随着市值而单调变化，而是呈现一个随着市值增加而先降后升的U形。可以推断，全样本期交易规模和波动率之间的正相关随市值单调递减主要来自2009年前这一子样本。2009年前后这一正相关随着市值变化规律的变动很可能来自中国A股市场的结构性变化。

市值越小的股票交易规模对波动率影响越大可以从流动性角度给予解释，市值小的股票由于流动性较低而导致交易规模对价格影响更加显著，从而对波动率影响更显著。然而，交易规模对波动率影响随市值增加先降低后增加却很难归因于流动性。

对比表4的B栏和C栏，发现随着时间推移，交易规模对波动率的解释能力在降低，意味着中国A股市场交易规模包含股价的信息含量在降低。对此有两种可能的解释：第一，近年来程序化交易的盛行使得投资者很容易利用拆单技术隐藏其交易，从而大大降低了交易规模的信息含量。第二，大量增加的机构投资者之间的竞争引起交易规模包含的机构投资者交易的信息含量下降。

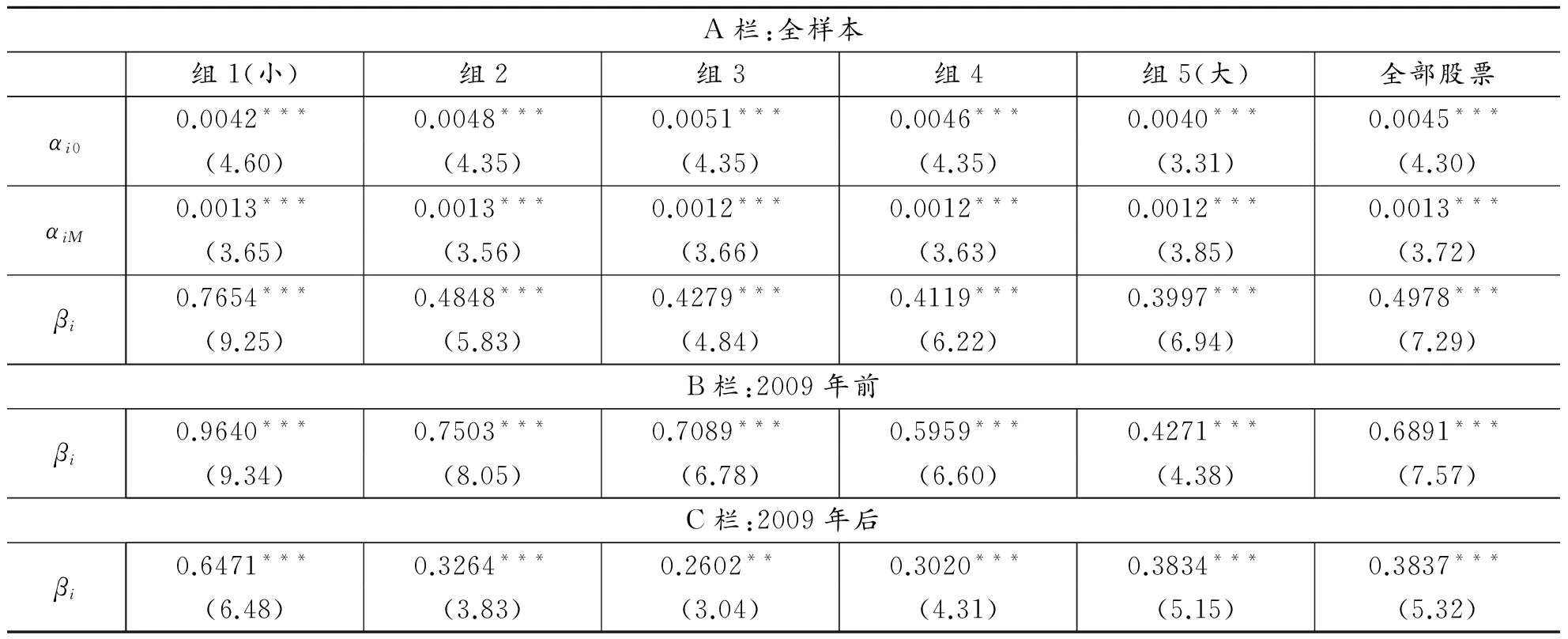
表4 交易规模和波动率相关性检验

注:*、**、***分别表示估计值在10%、5%和1%水平下显著。

2.交易次数波动率相关性检验。Jones等(1994)[27]、Chan和Fong (2000)[9]都发现交易次数对于波动率具有解释能力，而且中国是一个个人投资者占比特别大的市场，因此交易次数更可能对波动率产生显著影响。为了检验交易次数和波动率之间的相关性，每年对每只股票进行如下回归：

(5)

式(5)将式(3)中的交易量vlm换做交易次数NT，其余变量含义保持不变。表5的A、B和C栏分别给出了全样本、2009年前子样本和2009年后子样本中交易次数和波动率相关性检验的结果，每一栏结果都分为全部股票以及5个市值组合。A栏中间两行显示全样本期周一虚拟变量的系数不论是在全部股票还是5个市值组合当中都是1%水平显著为正，说明A股市场存在周一效应，和表2、表4结果一致。A栏最后两行最后一列给出交易次数的系数估计值为0.0261，在1%水平上显著，说明全部股票组合中交易次数越多伴随着波动率越高。5个市值组合中交易次数都显著为正，说明交易次数和波动率之间的强烈正相关同样存在于5个市值组合中。有趣的是，随着市值增加，交易次数的估计系数单调降低，表明股票市值越大交易次数对波动率解释力越弱，股票市值越小交易次数对波动率解释力越强。这与噪音交易者偏爱小市值股票且频繁交易导致波动率变化是一致的。

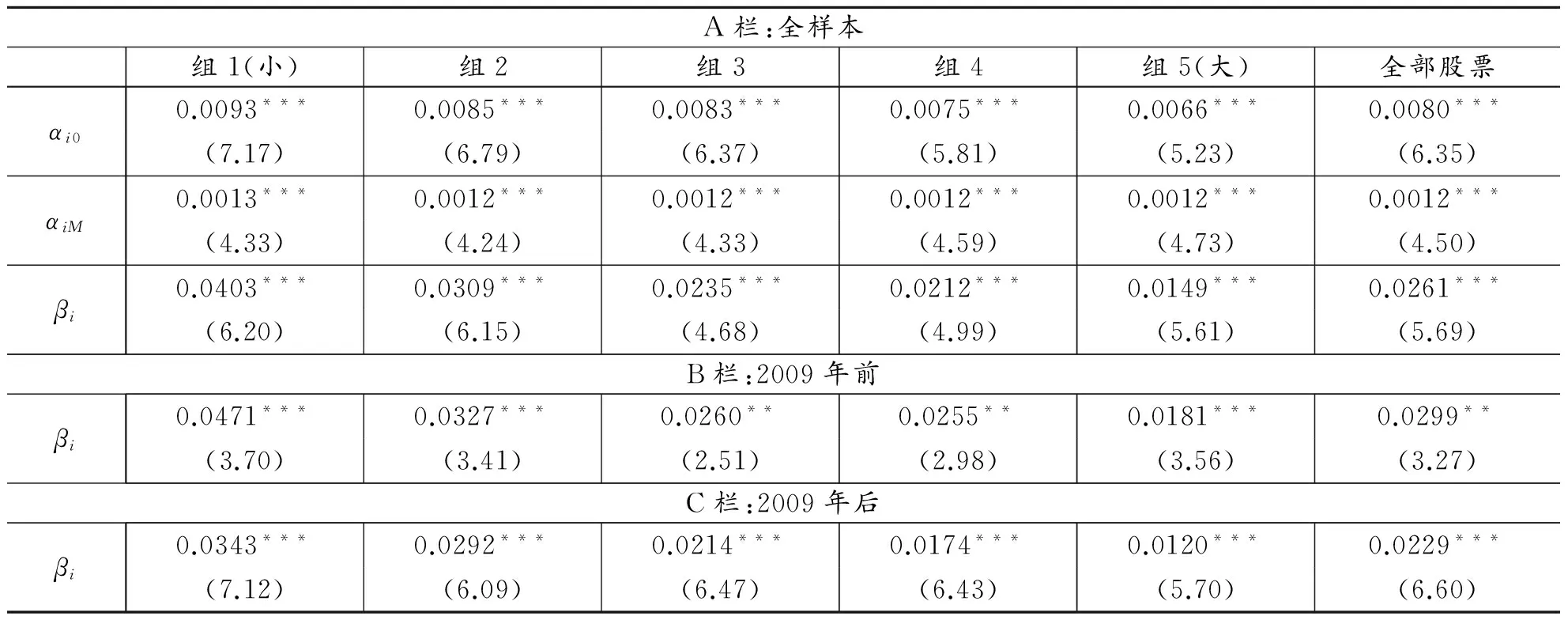
表5 交易次数和波动率相关性检验

注:*、**、***分别表示估计值在10%、5%和1%水平下显著。

表5的B栏给出了2009年前这一子样本的交易次数的系数估计值。全部股票组合中交易次数估计值为0.0299，在5%水平上显著为正。5个市值组合中除了第3、4组的交易次数系数估计值在5%水平上显著为正之外，其他组合的交易次数估计值都在1%水平上显著为正。这表明2009年前这一子样本中交易次数对波动率的解释力度并不强。5个市值组合的交易次数系数估计值同样表现出随着市值增加而单调减小的模式，说明股票市值越大交易次数对波动率影响越弱，这与全样本结果一致。

表5的C栏给出了2009年后这一子样本中交易次数系数估计值，最后一列给出全部股票交易次数估计值为0.0229，在1%水平上显著为正。5个市值组合中交易次数系数估计值也都在1%水平上显著为正，而且系数估计值随着市值增加而单调减小，表明股票市值越大交易次数对波动率影响越弱。对比2009年前后的结果，发现交易次数的系数估计值随时间推移而减小，表明交易次数对波动率的影响在减弱。根据第二部分的理论分析，这可能是伴随着个人投资者交易占比下降，而这与交易规模对波动率影响降低而体现的机构投资者交易占比增加是一致的。本文发现的交易次数和波动率正相关，与Jones等(1994)[27]在美国NASDAQ市场上的发现是一致的。本文为电子指令驱动市场交易次数和波动率正相关提供了直接证据。

3.交易规模对比交易次数：谁和波动率相关性更强？表4和表5分别证明了中国A股市场交易规模和交易次数各自和波动率的正相关，然而，这两个变量是否包含了同样的信息呢？或者说，这两个变量谁包含了更多的信息？Jones等(1994)[27]发现在美国市场交易次数包含了几乎所有信息，导致交易规模失去对于波动率的解释力度。那么这一结论是否适用于中国A股市场呢？为了检验这一结论，下面我们将交易规模AV和交易次数NT同时作为解释变量，每年对每只股票进行如下回归：

(6)

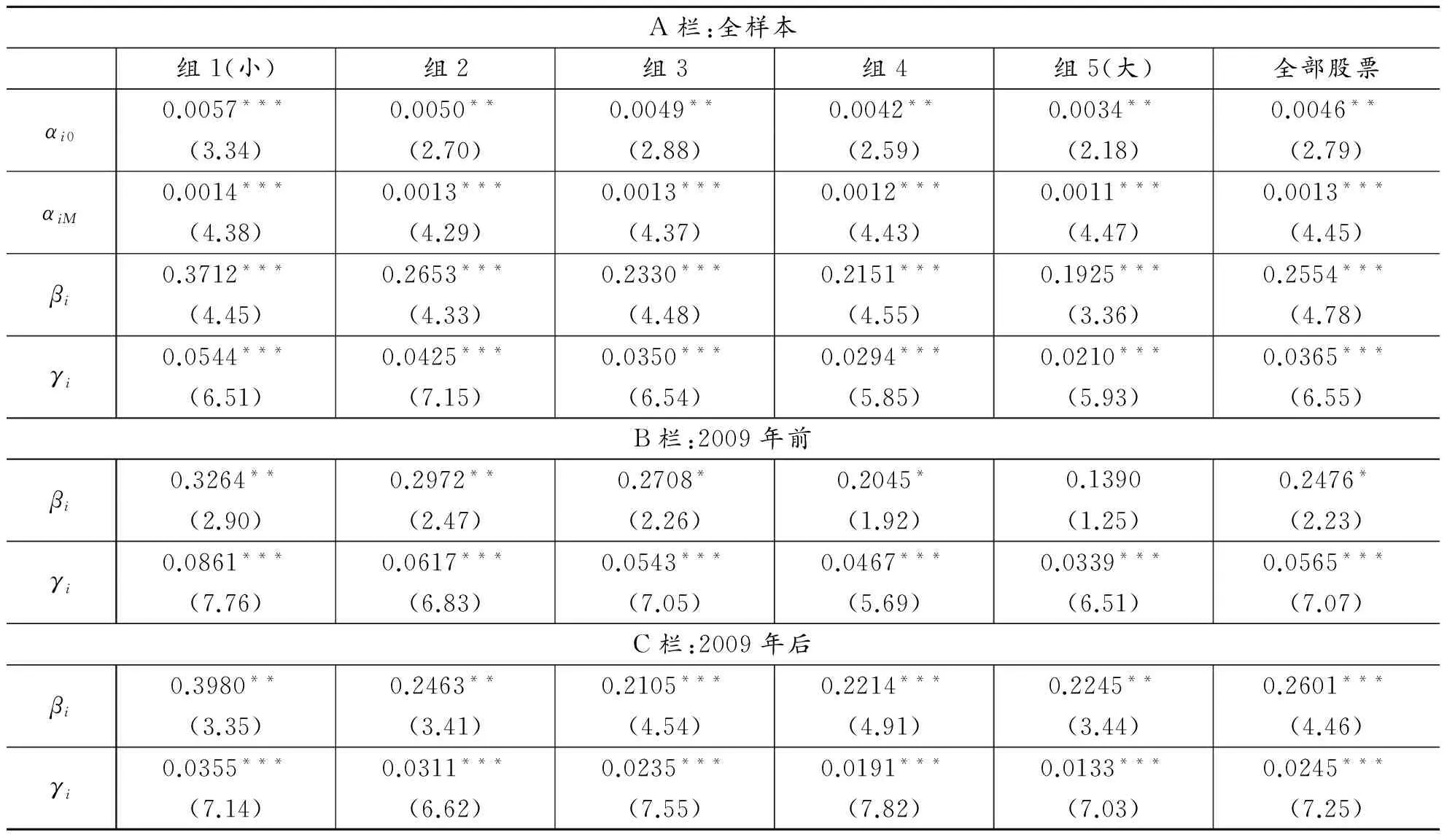
表6 交易次数+交易规模和波动率相关性检验

注:*、**、***分别表示估计值在10%、5%和1%水平下显著。

表6给出了交易规模和交易次数同时作为解释变量的估计结果，A、B和C栏分别对应全样本、2009年前的子样本和2009年后的子样本。A栏中周一虚拟变量的估计值和此前结果类似，说明A股波动率存在周一效应。A栏最后一列倒数4行显示当交易规模和交易次数同时作为解释变量时，交易规模和交易次数的系数估计值分别为0.2554和0.0365，都在1%水平上显著为正，表明二者都对波动率具有解释能力，任何一个变量不能吸收掉另外一个变量对波动率的解释力度。而且5个市值组合中同样如此，表明交易规模和交易次数对波动率的解释力度并存且不受市值影响。这与Jones等(1994)[27]在美国NASDAQ市场上的发现不同，该文发现虽然交易规模和交易次数分别都与波动率正相关，但是二者同时作为解释变量时，交易规模的解释力会被交易次数吸收掉。在交易规模和交易次数同时作为解释变量时，二者的估计系数都随着市值增加而单调递减，说明不论是交易规模还是交易次数对波动率的影响都随市值增大而减弱。

表6的B栏最后一列表明在2009年前这个子样本中，交易次数的出现导致交易规模不再具有显著为正的系数，而且此时交易规模只是在小市值股票中保持了对波动率的影响，这与Jones等(1994)[27]在美国NASDAQ市场的发现是一致的。交易次数的系数估计值仍然是显著为正的，不论是全部股票还是5个市值组合都是如此，表明交易次数比交易规模在2009年前这一子样本内具有更多的价格信息。同时，交易规模和交易次数的系数估计值都随着市值增加而减小。

表6的C栏最后一列表明在2009年后这个子样本中，交易次数并未吸收掉交易规模对波动率的解释力，这与Jones等(1994)[27]在美国NASDAQ市场的发现不同。所有市值组合中交易规模和交易次数的系数估计值都显著为正，表明交易规模和交易次数对于波动率同时具有解释能力并不受市值影响。交易次数的系数估计值随市值增加而单调递减，与表5结果一致。交易规模的系数估计值却出现了随市值增加而先降后升，与表4的C栏结果一致，这意味着2009年后交易规模对波动率的影响随市值增加而先降后升并不受交易次数的影响。

对比表6的B栏和C栏，发现交易次数的系数估计值不论在全部股票还是在5个市值组合中都是减小的，这与表5结果一致，说明交易次数对于波动率的影响在减弱，可能来自个人投资者对市场的影响在减弱。而交易规模的系数估计值虽然在全部股票中增加，但是5个市值分组中除了第1、第4和第5组是增加之外，第2、第3组却在减小，这与表4结果不同。但是，交易规模的系数估计值显著性却随时间而增加，说明交易规模对波动率的影响趋于稳健。结合表4和表5，交易次数对波动率解释力的减小不受交易规模的影响，但交易规模对波动率的影响减弱的结论受到交易次数的影响，再次说明交易次数对波动率的影响比交易规模显著。

为了分析价格冲击对交易规模和波动率相关性的影响，我们在式(6)中加入价格冲击指标进行如下回归：

(7)

式(7)中的PIi,t指的是股票i在日期t的价格冲击指标，根据Florackis等(2011)[40]，定义为收益率的绝对值(百分数)和换手率的比值。

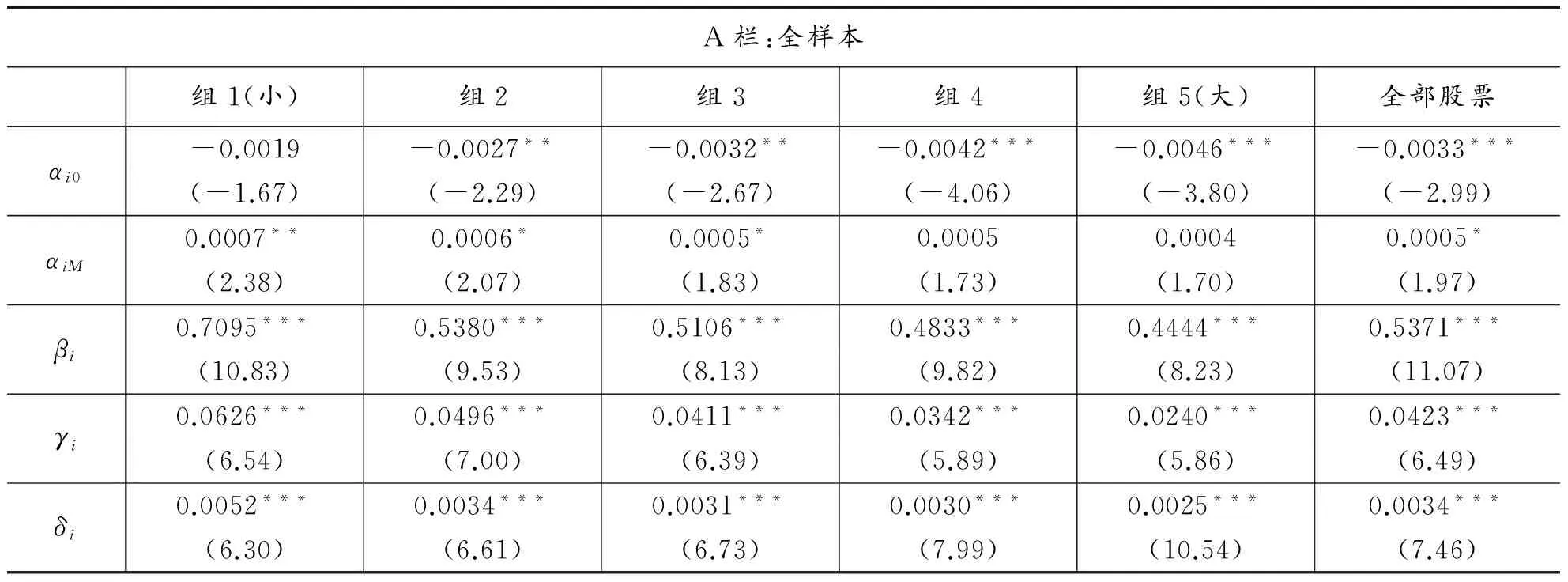
表7 交易次数+交易规模和波动率相关性检验：控制价格冲击

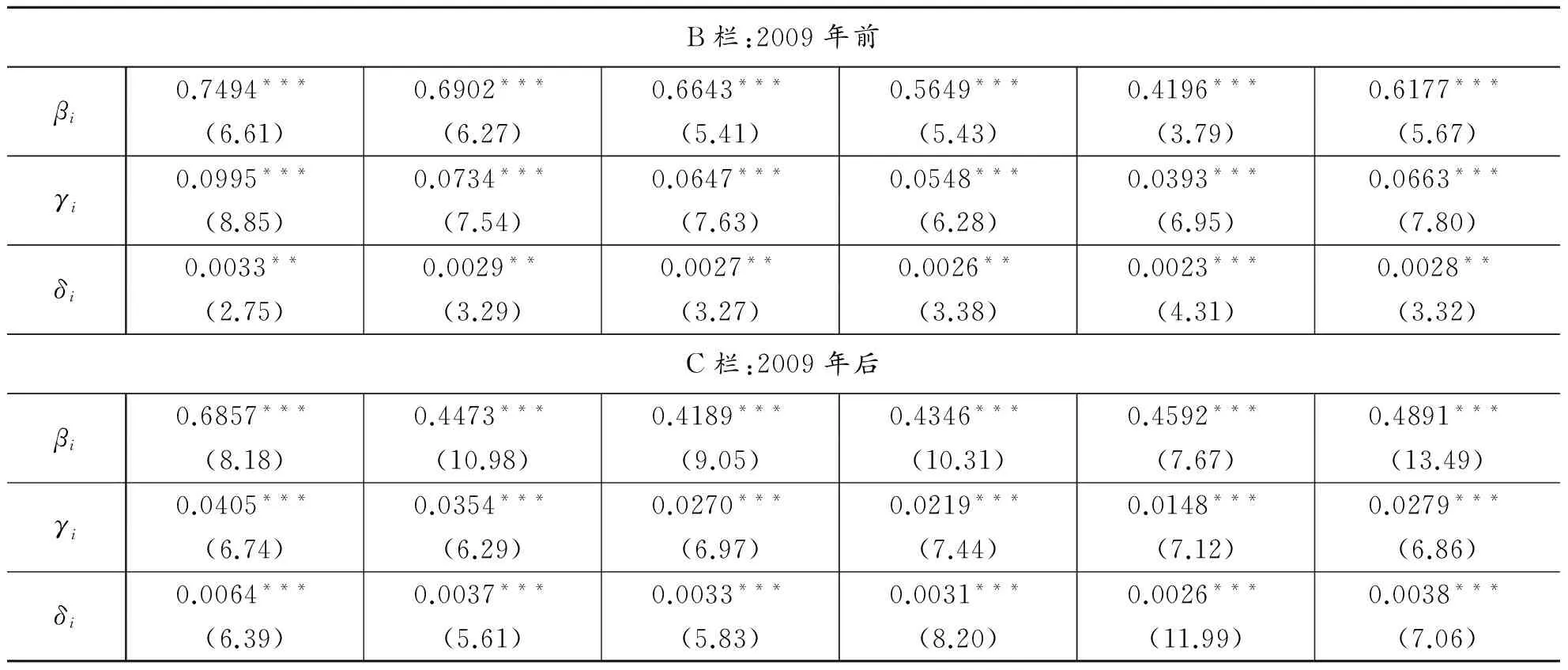
(续表)

注:*、**、***分别表示估计值在10%、5%和1%水平下显著。

表7给出了控制价格冲击之后的结果，A、B和C栏分别对应全样本、2009年前、后两个子样本。控制价格冲击之后，A栏周一虚拟变量所在的行显示除了最小市值股票组合之外，其他组合全部不再显著，表明波动率的周一效应在考虑价格冲击之后消失了，意味着波动率的周一效应很可能来自价格冲击。A栏中不论是全部股票还是5个市值组合交易规模的系数都比表6中更大，且显著性更强，表明在考虑价格冲击后交易规模对波动率解释能力增强了，这也意味着价格冲击能影响交易规模和波动率的相关性，证明了之前的推断。交易次数的系数估计值在加入价格冲击之后也增大了，与交易规模系数类似。价格冲击所在的行显示不论全部股票还是5个市值组合价格冲击的系数都是显著为正，这是合理的结果。价格冲击指标越大，单位换手率产生的价格变化越大，自然就对应着较高的波动率，因此价格冲击和波动率正相关。A栏的结果还显示，交易规模、交易次数和价格冲击的系数估计值都随市值增加而减小，表明这三个变量对波动率的影响随市值增大而减小。

表7的B栏显示，考虑价格冲击之后2009年前这一子样本中交易规模的系数不论全部股票还是5个市值组合都是显著的，与表6的B栏中的交易规模的系数相比，显著性大大增强。这说明交易规模对于波动率的影响来自价格冲击。表7的B栏中交易次数的系数估计值也比表6更大。表7的C栏显示，考虑价格冲击之后2009年后这一子样本中交易规模和交易次数的系数估计值全部显著，也比表6更大。对比表7和表6的结果，可以认为价格冲击影响交易规模和交易次数对波动率的解释，而交易规模受到的影响更明显。对比B栏和C栏，除了最大市值组合之外，交易规模和交易次数的系数估计值都随时间推移在减小，这与表4至表6的结果是一致的。

4.金融危机的影响。为了分析金融危机对交易规模和波动率相关性的影响，我们在式(7)中加入交易规模和金融危机虚拟变量的交叉项、交易次数和金融危机虚拟变量的交叉项，采用全样本进行如下回归：

σi,t=αi0+αiMMDt+βiAVi,t+βicAVi,t·Ct+γiNTi,t+

(8)

式(8)中Ct是金融危机虚拟变量，参考Barrot等(2016)[41]研究，Ct在2008年9月到2009年4月之间等于1，否则取值为0，其他变量和(7)式相同。

表8给出了式(8)的估计结果。其中交易规模、交易次数和价格冲击的系数估计值与表7的A栏基本一致，说明控制金融危机并不影响交易量和波动率之间的关系。βic所在的行显示，不论对于5个市值分组还是所有股票而言，金融危机虚拟变量和交易规模交叉项的系数估计值都不显著；γic所在的行显示金融危机虚拟变量和交易次数的交叉项系数估计值同样不显著。这说明交易量和波动率之间的正相关在金融危机期间和其他时期并无显著差异。

表8 交易次数+交易规模和波动率相关性检验：控制价格冲击和金融危机

注:*、**、***分别表示估计值在10%、5%和1%水平下显著。

5.稳健性分析。本文通过不同的波动率度量指标和不同的计量分析方法进行稳健性检验。实际上，表3～表7中已经进行了分样本的稳健性检验。将(7)式中的极差波动率换成残差波动率得到的分析结果和表7类似，具体结果不再赘述。

表9 系数估计值t>2百分比(%)

表9是对式(7)中所有个股估计系数t统计量大于2的百分比统计结果。具体过程是，首先找出每年至少有60个观测的个股时间序列，每年对每只个股进行时间序列回归，得到每一个回归的经过Newey-West矫正的t统计量，然后计算t统计量大于2的百分比。注意，只要t统计量大于2的百分比高于5%即可拒绝系数为0的原假设，但我们取临界值为20%以保证结论可靠。

表9给出了式(7)的交易规模和交易次数的系数估计值t>2的统计结果。全样本所在的行中交易规模系数估计值t>2百分比最小为41.82%，因此不论全部股票还是5个市值组合的系数估计值都拒绝系数为0的假设，在两个子样本中也是如此。表9中交易次数的系数估计值t>2百分比更大，同样拒绝其系数为0的原假设。表9的结果进一步印证了表7的结果，表明结论是稳健的。

五、 结 论

基于2001-2016年沪深A股所有个股数据，计算经过横截面和时间序列二维丛集性矫正的稳健标准误，本文首先证明了中国A股市场个股具有交易量与波动率正相关关系，接着证明这种正相关也存在于指数中。将交易量分解为交易规模和交易次数，发现交易规模和交易次数单独作为解释变量时，这两个变量也都与波动率存在稳健的正相关关系，这与美国市场的结论一致，但本文的发现证明了纯粹的电子指令驱动市场同样存在交易量(总股数、交易规模和交易次数)和波动率之间的正相关。将交易规模和交易次数同时作为解释变量，全样本期间二者都对波动率具有解释能力。虽然在2009年前子样本期间交易次数吸收掉了交易规模对波动率的解释能力，但是2009年后子样本期间交易规模和交易次数同时具有对波动率的解释能力，这与美国市场是不同的。进一步地，在考虑价格冲击之后，交易规模对波动率的解释能力显著增强，并且在全样本和子样本中都不会因为交易次数而失去对波动率的显著解释能力，这表明交易规模对波动率的影响可归因于价格冲击。比较而言，中国A股市场上既存在与美国市场共有的交易量波动率正相关，也存在交易规模和波动率之间的正相关性不因交易次数而消失的特有现象。基于这一发现，本文的结论说明，针对中国A股市场的资产定价理论模型应该考虑交易规模和交易频率都包含价格信息，且交易次数对价格变化的影响更大，同时价格冲击也应该被考虑在内。

我们在A股市场发现平均单笔交易量也就是交易规模同样具有对波动率的解释能力，与美国市场不同。这可能来自两个市场的投资者结构差异。美国市场相对成熟，以机构投资者为主，中国市场以个人投资者为主。在一个个人投资者在交易中占绝对多数的市场中，交易规模能够体现机构投资者的交易，因此根据信息不对称模型，机构投资者的交易在展现信息的同时伴随着价格变化，这就出现了交易规模和波动率的正相关。交易规模对波动率的影响并未因为交易次数而消失可以视作信息不对称模型的一种事实依据，因此本文结论在一定程度上支持交易量与波动率正相关的信息不对称模型。

[1]ENGLE R F.Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation[J].Econometrica,1982,50(4):987-1007.

[2]朱钧钧,谢识予.中国股市波动率的双重不对称性及其解释——基于 MS-TGARCH 模型的 MCMC 估计和分析[J].金融研究,2011(3):134-148.

[3]张宗新,王海亮.投资者情绪,主观信念调整与市场波动[J].金融研究,2013(4):142-155.

[4]郑挺国,尚玉皇.基于宏观基本面的股市波动度量与预测[J].世界经济,2014(12):118-139.

[5]FRENCH K R,ROLL R.Stock return variances:the arrival of information and the reaction of traders[J].Journal of Financial Economics,1986,17(1):5-26.

[6]ADAM K,MARCET A,NICOLINI J P.Stock market volatility and learning[J].The Journal of Finance,2016,71(1):33-82.

[7]BOLLERSLEV T,LI J,XUE Y.Volume,volatility and public news announcements[EB/OL].(2016-06-23)[2017-05-01].http://EconPapers.repec.org/RePEc:aah:create:2016-19.

[8]RANNOU Y,BARNETO P.Futures trading with information asymmetry and OTC predominance:another look at the volume/volatility relations in the European carbon markets[J].Energy Economics,2016,53(1):159-174.

[9]CHAN K,FONG W-M.Trade size,order imbalance,and the volatility-volume relation[J].Journal of Financial Economics,2000,57(2):247-273.

[10]FOUCAULT T,SRAER D,THESMAR D J.Individual investors and volatility[J].The Journal of Finance,2011,66(4):1369-1406.

[11]祁斌,黄明,陈卓思.机构投资者与股市波动性[J].金融研究,2008(9):54-64.

[12]林忠国,韩立岩.机构交易的正面效应:波动率和市场效率的视角[J].系统工程理论与实践,2011(4):606-616.

[13]谭松涛,崔小勇,孙艳梅.媒体报道,机构交易与股价的波动性[J].金融研究,2014(3):180-193.

[14]蔡庆丰,宋友勇.超常规发展的机构投资者能稳定市场吗?[J].经济研究,2010(1):90-101.

[15]史永东,王谨乐.中国机构投资者真的稳定市场了吗?[J].经济研究,2014(12):100-112.

[16]LAMOUREUX C G,LASTRAPES W D.Heteroskedasticity in stock return data:volume versus GARCH effects[J].The Journal of Finance,1990,45(1):221-229.

[17]赵留彦,王一鸣.沪深股市交易量与收益率及其波动的相关性:来自实证分析的证据[J].经济科学,2003(2):57-67.

[18]王燕辉,王凯涛.股票交易量对收益率波动性的影响——对深市个股的实证分析[J].金融研究,2004(12):81-88.

[19]杨炘,王邦宜.交易量与股价波动性:对中国市场的实证研究[J].系统工程学报,2005(5):530-534.

[20]TAUCHEN G E,PITTS M.The price variability-volume relationship on speculative markets[J].Econometrica:Journal of the Econometric Society,1983,51(2):485-505.

[21]KYLE A S.Continuous auctions and insider trading[J].Econometrica,1985,53(6):1315-1335.

[22]ADMATI A R,PFLEIDERER P.A theory of intraday patterns:volume and price variability[J].Review of Financial Studies,1988,1(1):3-40.

[23]SCHEINKMAN J A,XIONG W.Overconfidence and speculative bubbles[J].Journal of Political Economy,2003,111(6):1183-1220.

[24]BANERJEE S,KREMER I.Disagreement and learning:dynamic patterns of trade[J].The Journal of Finance,2010,65(4):1269-1302.

[25]陈梦根,毛小元.股价信息含量与市场交易活跃程度[J].金融研究,2007(3):125-139.

[26]唐齐鸣,刘亚清.市场分割下 A、B 股成交量、收益率与波动率之间关系的 SVAR 分析[J].金融研究,2008(2):113-126.

[27]JONES C M,KAUL G,LIPSON M L.Transactions,volume,and volatility[J].Review of Financial Studies,1994,7(4):631-651.

[28]许香存，陈志娟.沪港通对股票市场波动性和流动性影响的实证研究[J].浙江工商大学学报，2016(6)：76-83.

[29]黄顺武，王梦莹，昌望.机构投资者的信息优势研究——来自上市公司重大股权收购的证据[J].证券市场导报，2015(8):45-51,77.

[30]LIPPMAN S A,MCCALL J J.An operational measure of liquidity[J].The American Economic Review,1986,76(1):43-55.

[31]ALIZADEH S,BRANDT M W,DIEBOLD F X.Range-based estimation of stochastic volatility models[J].The Journal of Finance,2002,57(3):1047-1091.

[32]SCHWERT G W.Stock volatility and the crash of ’87[J].Review of Financial Studies,1990,3(1):77-102.

[33]AVRAMOV D,CHORDIA T,GOYAL A.The impact of trades on daily volatility[J].Review of Financial Studies,2006,19(4):1241-1277.

[34]THOMPSON S B.Simple formulas for standard errors that cluster by both firm and time[J].Journal of Financial Economics,2011,99(1):1-10.

[35]CAMERON A C,GELBACH J B,MILLER D L.Robust inference with multiway clustering[J].Journal of Business & Economic Statistics,2011,29(2):238-249.

[36]NEWEY W K,WEST K D.A simple,positive semi-definite,heteroskedasticity and autocorrelation consistent covariance matrix[J].Econometrica,1987,55(3):703-708.

[37]GRUNDY B D,MCNICHOLS M.Trade and the revelation of information through prices and direct disclosure[J].Review of Financial Studies,1989,2(4):495-526.

[38]HOLTHAUSEN R W,VERRECCHIA R E.The effect of informedness and consensus on price and volume behavior[J].Accounting Review,1990,65(1):191-208.

[39]KIM O,VERRECCHIA R E.Market reaction to anticipated announcements[J].Journal of Financial Economics,1991,30(2):273-309.

[40]FLORACKIS C,GREGORIOU A,KOSTAKIS A.Trading frequency and asset pricing on the London Stock Exchange:evidence from a new price impact ratio[J].Journal of Banking & Finance,2011,35(12):3335-3350.

[41]BARROT J-N,KANIEL R,SRAER D.Are retail traders compensated for providing liquidity?[J].Journal of Financial Economics,2016,120(1):146-168.

(责任编辑毕开凤)

WhatCausestheInfluenceofTradingVolumeonVolatilityTradeSizeorNumberofTransactions？

MA Chang-feng， CHEN Zhi-juan

(SchoolofFinance，ZhejiangGongshangUniversity，Hangzhou310018，China)

Based on the daily data of individual stocks and indices from 2001 to 2016 at Shanghai and Shenzhen Exchange， this paper establishes the contemporaneous positive correlation between trading volume and volatility. Decomposing volume into trade size and number of transactions， we find that either trade size or number of transactions is able to explain volatility respectively. When they both serve as independent variables to explain volatility， trade size has power to explain volatility in the after-2009 sample and whole sample， though it has no explaining power in the before-2009 sample. The explaining power of number of transactions on volatility manifests not only in both sub-samples but also in the whole sample after taking price impact into account， indicating the co-existence of the explaining power of both trade size and number of transactions on volatility within the China stock market. We also show that the positive correlation between trading volume and volatility during financial crisis is not significantly different from the normal period．

trading volume; volatility; trade size; number of transactions; financial crisis

F839.5

A

1000-2154(2017)09-0072-14

2017-05-04

国家自然科学基金青年项目“盈余公告期间个人投资者买入需求流动性？卖出提供流动性？”(71401155)；教育部人文社科基金青年项目“证券价格波动机理研究：基于个人投资者交易行为的视角”(11YJC790133);浙江省高校人文社会科学重点研究基地(浙江工商大学应用经济学)资助项目(JYTjr20111310)

马长峰，男，讲师，经济学博士，主要从事资产定价研究；陈志娟，女，副教授，经济学博士，主要从事资产定价和风险管理研究。

10.14134/j.cnki.cn33-1336/f.2017.09.007

马长峰，陈志娟.交易量影响波动率的成因：交易规模还是交易次数？[J].商业经济与管理，2017(9)：72-85.