浅谈“设而不求”的解题方法

☉湖南省永顺县第一中学 石家文

浅谈“设而不求”的解题方法

☉湖南省永顺县第一中学 石家文

“设而不求”是一种在解析几何中常见的解题方法，笔者通过多年的教学和研究，体会到这种解题方法不仅用于解决解析几何问题，而且函数、不等式等问题也经常用到，下面笔者从六个方面，谈一谈对这种解题方法的体会.

一、“设而不求”之“引参法”

通过引入参数，架设沟通桥梁.

解析：不防设（fa）=（fb）=（fc）=t，在同一坐标系中作出函数y=（fx）及y=t的图像，如图1所示.

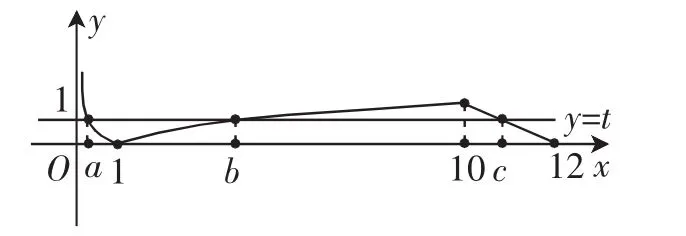
图1

由图1知f（a）=f（b）⇒-lga=lgb，即a-1=b，即ab=1，所以abc=c.

由图1知c的取值范围是（10，12），所以abc的取值范围是（10，12）.

点评：这里参数t的引入，目的便于作图，把a，b，c在图上画出来，让我们据图说话，一幅图真的是胜过千言万语，而参数t就像一根杠杆，起到了四两拨千斤的作用.

二、“设而不求”之“换元法”

通过换元，优化式子结构.

故所求的最小值为3.

点评：设辅助元对分母实施代换，把多项式分母化为单项式分母，优化了式子的结构，为后续的恒等变形和放缩变形创造条件.

三、“设而不求”之“逆代法”

当直线与曲线或曲线与曲线的交点不易解出来或无法解出来时，可以先把交点坐标设出来，然后往回代入，笔者称之为“逆代法”.例如点差法等.3已知椭圆C=1，试确定m的取值范围，

例使得椭圆上有两个不同的点关于直线y=4x+m对称.

解析：设A（x1，y1），B（x2，y2）是椭圆上关于直线l对称的两点，M（x0，y0）为弦AB的中点，则有且

点评：由于用方程组法求交点坐标很困难，故干脆不考虑方程组法，而是一开始就把交点坐标设出来，然后，由交点在曲线上，故把所设点的坐标代入曲线方程，而交点在直线上常转化成三点共线或向量共线，所以说这是一种以逆向思维来处理问题的解题方法，而此处的解法常叫“点差法”.

在数学教学中教师是课堂活动中的主要负责人，也是学生进行自主学习的指导者，只有在教师的安排和指导下，学生才能够有效实现自主学习，培养学生的学习能力。因此需要加强教师对学生自主学习能力培养的重视，明确课堂教学目标，积极进行数学教学策略的创新，结合学生的学习能力，创设课堂情境，组织教学活动，引导学生进行自主学习，培养学生的自主学习意识，促使学生在不断的学习中提高自身能力，实现对学生的素质教育。

四、“设而不求”之“方程组法”

涉及直线与圆锥曲线的交点（包括切点）问题一般先列方程组，然后消元得一个一元二次方程，此时，我们常把它的两根设出来，然后利用韦达定理来处理，这是解析几何问题最常用的解法，通常称为“方程组法”.

例4已知椭圆C的方程为=1，直线l：y=kx+m（|k|≤）与椭圆C交于A，B两点，以线段OA，OB为邻边作平行四边形OAPB，顶点P恰好在椭圆C上，O为坐标原点，求|OP|的取值范围.

点评：直线与圆锥曲线的位置关系的相关知识一直是高考的重点与热点内容，涉及问题有弦长问题、弦中点问题、最值问题、范围问题、定值问题、定点问题等，大都采用设而不求与韦达定理相结合的方法来处理.

五、“设而不求”之“参数方程法”

当问题涉及动直线与曲线上动点有关问题时，常利用参数方程来减少所设参数的个数的方法来解决，常称之为“参数方程法”.

例5已知抛物线y2=2px及定点A（a，b），B（-a，0）（ab≠0；b2≠2pa），M是抛物线上的点，设直线AM，BM与抛物线的另一交点分别为M1，M2.求证：当M点在抛物线上变动时（只要M1，M2存在且M1≠M2） 直线M1M2恒过定点，并求出该定点的坐标.

故设点M（2pt2，2pt），M（，2pt），M（，2pt）（.t，1122t1，t2互不相等）

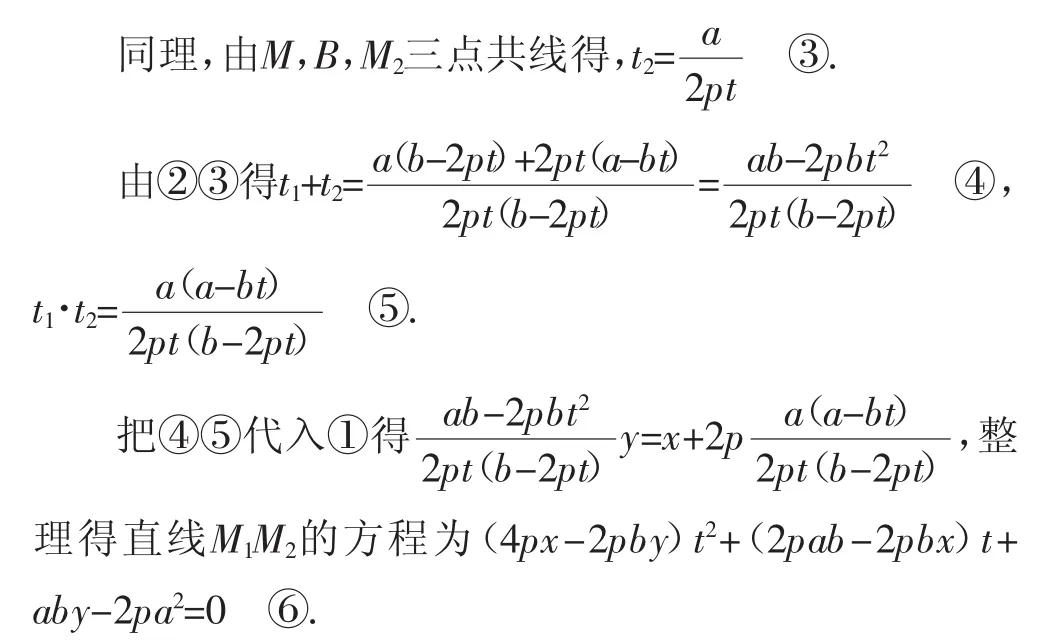
点评：①为了避免求坐标，这里采用了“设而不求”，把相关点的坐标先设出来，为了少设字母，这里充分利用了曲线参数方程；为了表示点在直线上，这里采用三点共线，进而有向量共线，从而避免了复杂的运算.②以参数t为主元，反客为主的方式求得直线M1M2过定点（a，）是研究定点问题的重要方法.③灵活运用类比方法，减少了运算量，是本题解法的一大亮点，值得大家学习和借鉴.

六、“设而不求”之“记零点法”

研究函数问题，常需求函数（特别是导函数）的零点，而此时的零点又难以解出，可以把零点设出来然后回头代入的方法，笔者称之为“记零点法”.

例6设函数（fx）=e2x-alnx.

（1）讨论（fx）的导函数f（′x）零点的个数；

解析：（1）（fx）的定义域为（0，+∞），f′（x）=2e2x-（x＞0）.由f′（x）=0，得2xe2x=a.令g（x）=2xe2x，则g′（x）=（4x+2）e2x＞0（x＞0），从而g′（x）在（0，+∞）上单调递增，所以g（x）＞g（0）=0.

当a＞0时，方程g（x）=a有一个根，即f′（x）存在唯一零点；

当a≤0时，方程g（x）=a没有根，即f′（x）没有零点.

（2）由（1），可设f′（x）在（0，+∞）上的唯一零点为x0.当x∈（0，x0）时，f′（x）＜0；当x∈（x0，+∞）时，f′（x）＞0.故f（x）在（0，x0）上单调递增，在（x0，+∞）上单调递增，所以f（x）min=f（x0）.

七、结束语

综上所述，“设而不求”就是在解题过程中，通过引入辅助元而不求解，只借助它的桥梁作用，使问题得到迅速解决的解题方法.其实，这是从操作方式的角度来说的.若从思维方式的角度去看，它是一种正反结合的思维方式，是顺着不行逆着来；再从功能的角度来看，无论是架设沟通桥梁的引参法还是调整结构的换元法，都是为了避免繁杂的运算而达到简化解题过程的目的；最后从应用范围的角度看，无论是代数（函数、方程、不等式）方面，还是几何（平面几何、解析几何、立体几何）方面，均有设而不求”的应用（限于篇幅，有的没有举例）.因此，“设而不求”是一种运用灵活而广泛的解题方法，若能恰当运用它，则能使问题的解决变得简捷明快.