有关抛物线焦点弦问题的处理策略

☉江苏省如东县马塘中学 黄一白

有关抛物线焦点弦问题的处理策略

☉江苏省如东县马塘中学 黄一白

对一道问题从不同角度进行探究、运用不同的方法进行解答，有利于学生巩固基础，将所学知识由点到线，由线到面，形成网络，在解题中迅速找到最优解法，进而提高自身分析问题、解答问题的能力.本文以2017年高考全国I卷中的一道抛物线问题为例，就其中所涉及的解题方法详细说明.

题目 （2017年全国I卷理10题）已知F为抛物线C：y2=4x的焦点，过点F作两条互相垂直的直线l1，l2，直线l1与抛物线C交于A、B两点，直线l2与抛物线C交于D、E两点，则|AB|+|DE|的最小值为（ ）.

A.16B.14C.12D.10

与抛物线的焦点弦有关的问题，是高考对抛物线考查的重要视角.对于弦长，既可以利用弦长公式，也可以利用焦半径公式，还可以从极坐标和参数方程的视角来求解.下面给出这几种具体的解答方法.

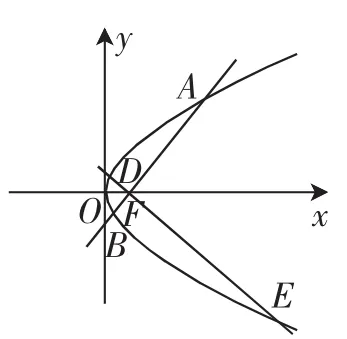
图1

一、直接求弦长

解法1：如图1，由题意可知两条直线的斜率存在，且不为0.设直线l1：y=k（x-1）与抛物线方程y2=4x联立，消y得k2x2-（2k2+4）x+k2=0.

设A（x1，y1），B（x2，y2），则x1+x2=，x1x2=1，所 以|AB|=

同理，|DE|=4k2+4.

评析：因为AB与DE垂直，两斜率互为负倒数，所以对于|DE|的求解，可直接将|AB|=+4中的k用-替换，从而简化解题过程.另外在应用均值不等式求最值时，要注意等号取得的条件.

二、利用抛物线定义

解法2：设直线l1：y=k（x-1）与抛物线方程y2=4x联立，消y得k2x2-（2k2+4）x+k2=0.

设A（x1，y1），B（x2，y2），则x1+x2=

同理，|DE|=4k2+4.

评析：对于抛物线的弦长问题，要重点把握抛物线的定义：到焦点的距离与到准线的距离相等，从而将问题转化求解.此方法简洁、直观，是解答此类问题的通法.

三、参数方程法

四、极坐标法

解法4：以抛物线y2=4x的顶点为极点，x轴正半轴为极轴，建立极坐标系.设|AF|=ρ1，|BF|=ρ2，∠AFx=θ，由抛物线的定义得ρ=ρcosθ+p，所以ρ=，ρ=12

所以|AB|=ρ1+ρ2=

评析：根据圆锥曲线的统一定义：到焦点的距离与到对应准线的距离之比为离心率e，得圆锥曲线的极坐标方程为ρ=，当0＜e＜1时，表示椭圆；当e＞1时，表示双曲线；当e=1时，表示抛物线.本题求解中利用抛物线的极坐标方程，表示出焦点弦的长度，从而将所求最值转化为三角函数求最值或利用均值不等式求最值问题.另外，当e=1时，ρ=，表示以焦点为极点、开口向左的抛物线；ρ=表示开口向上的抛物线；ρ=表示开口向下的抛物线.

五、特殊位置法

解法5：由抛物线的对称性可知，若|AB|+|DE|取得最大值，则此最值应在对称位置取得，即当AB与DE关于x轴对称时取得最大值，此时|AB|与|DE|相等，其中一条直线的斜率为1，另一条直线的斜率为-1.

设直线AB的斜率为1，则AB：y=x-1，与抛物线y2=4x联立消去y得x2-6x+1=0.设A（x1，y1），B（x2，y2），则x1+x2=6.由抛物线的定义知|AB|=x1+x2+p=8，所以|AB|+|DE|的最大值为16.

评析：在标准方程下的椭圆、双曲线、抛物线均为特殊的对称图形，其中椭圆和双曲线既关于坐标轴对称，也关于原点对称.抛物线关于x轴或y轴对称.本题作为一道客观题，只需要给出答案，不需解题过程，因此可采用小题小做的原则，从特殊位置入手.因为抛物线y2=4x关于x轴对称，所以该抛物线的通径、准线等，也关于x轴对称.对称图形的最值，也一定保留着对称性，对称图形的定值也渗透于对称性之中，因此利用圆锥曲线的对称性可以迅速求得某些定值和最值问题.

综上，在解题教学中，教师要善于引导学生对同一题目从不同视角进行探究，用多种方法进行解答，并在解题后进行反思，对各种方法通过繁简对比，从中选出最优的解法，进而提高自身解题能力.