拟复射影空间CQn中2-调和伪脐子流形

刘金梦，耿 杰，宋卫东

(1.安徽师范大学数学计算机科学学院，中国 芜湖 241000;2.安徽信息工程学院，中国 芜湖 241001)

拟复射影空间CQn中2-调和伪脐子流形

刘金梦1，耿 杰2，宋卫东1

(1.安徽师范大学数学计算机科学学院，中国 芜湖 241000;2.安徽信息工程学院，中国 芜湖 241001)

本文用活动标架法研究了拟复射影空间CQn中2-调和伪脐子流形，获得了这类子流形的一个积分不等式及推论，并得到了2-调和伪脐子流形是极小子流形的条件.

拟复射影空间;2-调和子流形；伪脐子流形

AbstractIn this paper, we study pseudo-umbilical submanifolds with 2-Harmonic in a quasi-complex projective space by method of moving frames. We get an integral inequality and ratioccination.Moreover,we also obtian the condition that pseudo-umbilical submanifolds with 2-Harmonic is minimum submanifolds.

Keywordsquasi-complex projective space; 2-Harmonic submanifolds; pseudo-umbilical submanifolds

设CQn是具有Kaehler度量的复n(n≥2)维黎曼复流形，若其曲率张量取为如下形式：

KABCD=a(gACgBD-gADgBC+JACJBD-JADJBC+2JABJCD)+

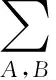
则称CQn为拟复射影空间[1].其中：g为CQn上的黎曼度量，J为CQn的复结构，a,b是CQn上的光滑函数，{λA}是CQn上的单位向量函数，称λA为CQn的生成元.

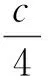
按照Eells和Lemeine在文献[2]中的设想，姜国英在文献[3-4]中给出了黎曼流形间2-调和映射的充要条件.由此条件，文献[5-7]主要研究了复空间形式的2-调和子流形.近年来不少学者开始研究拟复射影空间2-调和子流形的相关问题，得到了一些研究成果[8-9].

本文将继续讨论拟复射影空间的2-调和伪脐子流形，得到以下结果：

定理1设Mn是拟复射影空间CQn的紧致无边2-调和伪脐子流形，则有

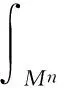
其中，S1为平均曲率向量方向的第二基本形式模长平方.

推论1设Mn是CQn中紧致无边的2-调和伪脐子流形，若S1<(n+3)a+|b|(n+1),则Mn是极小子流形.

推论2设Mn是CQn中具有平行平均曲率紧致无边的2-调和伪脐子流形，若S1<|b|(n+1),则Mn是极小子流形.

定理2设Mn是拟复射影空间CQn中2-调和伪脐子流形，若

则Mn是极小子流形.

1 预备知识

本文对各类指标取值范围约定如下：

A，B，C，…=1，…，n,1*,…,n*;i,j,k,…=1,…,n;α,β,γ,…=1*,…,n*.

设Mn是CQn中的实n维全实子流形，J为CQn的复结构.在CQn上选取局部正交标架场

e1,…,en,e1*=Je1,…,en*=Jen,

使得限制于Mn,{e1,…,en}与Mn相切.以{ωA}表示{eA}的对偶标架场，则CQn的结构方程为：

(1)

其中

ωij=ωi*j*,ωi*j=ωj*i,

KABCD=a(δACδBD-δADδBC+JACJBD-JADJBC+2JABJCD)+

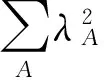
(2)

这里(JAB)为复结构，J是关于{eA}的变换矩阵，即

其中In为n阶单位矩阵.

将上述形式限制在Mn上，则有[10]

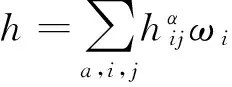
(3)

(4)

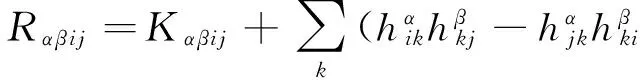
(5)

其中Rijkl,Rαβij分别是Mn的曲率张量场R和法曲率张量场关于{eA}的分量.进一步，Mn的平均曲率向量场ξ,平均曲率H,第二基本形式模长平方S可分别表示为

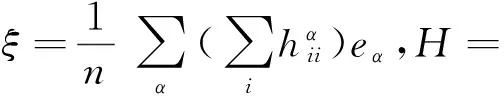
(6)

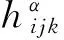
(7)

(8)

引理1[2]Mn是CQn中全实2-调和子流形的条件是

2 定理证明

下面总假设CQn是n维拟复射影空间，Mn是CQn中实n维紧致全实伪脐子流形，选取e1*与平均曲率ξ的方向重合，则

(9)

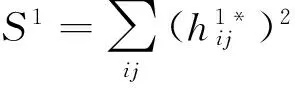
定理1的证明

因为

(10)

(11)

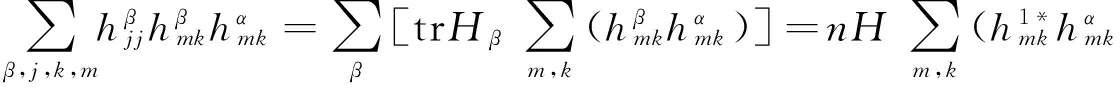
(12)

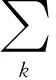
(13)

由式(9)～(13)及引理1的第二式，取α=1*,

对上式两端同时积分及Mn的紧致无边性，由Stokes定理可得：

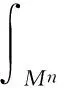
这就证明了定理1，推论1可直接由定理1得出.

推论2的证明

由于Mn具有平行平均曲率向量[11]，由式(1),对任意的α,有ω1*α=0,将其代入式(3)后得到

R1*βij=0, ∀β,i,j

(15)

由式(5)，(9)和(15)可得

若取i=1,有β=j≠1,或取j=1,有β=i≠1,但都有δ1iδβj-δ1jδβi≠0,从而得a=0.

将上式代入式(14)，我们得到

ΔH+H(|b|(n+1)-S1)≥0.

对上式两端同时积分及Mn的紧致无边性，由Stokes定理可得：

故若S1<|b|(n+1),Mn是极小子流形.

定理2的证明

利用式(7)将引理1的第一式改写为如下形式

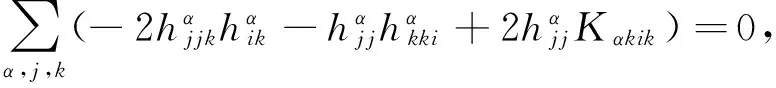
(16)

进一步，我们有

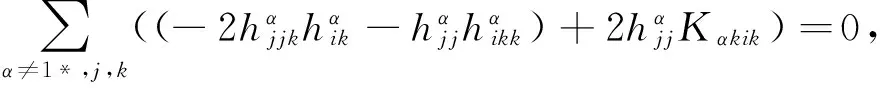
(17)

根据式(2),(9),(16)和(17)得到

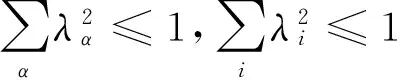
H[(2+n)H-2|b|(n-1)]≤0.

[1] 宋卫东，朱 岩.拟复射影空间CQn+p中的全实伪脐子流形[J].吉林大学学报(理学版)， 2012,50(4):673-676.

[2] EELLS J, LEMARE L. A report on harmonic maps[J].Bull London Math Soc, 1978,10:1-68.

[3] 姜国英.Rieman流形间的2-调和映射及其第一，第二变分公式[J].数学年刊， 1986,7(A):389-402.

[4] 姜国英.Rieman流形间的2-调和映射等距浸入[J].数学年刊， 1986,7(A):130-144.

[5] ZHU Y C, SONG W D. 2-Harmonic sunmanifolds in a Comples Space Form[J].J Math Res Expo, 2008,28(3):727-732.

[6] 胡亚举，王丽娟，宋卫东.复射影空间的2-调和全实力流形[J].大学学报， 2009,24(1):88-91.

[8] 马金生，宋卫东.拟复射影空间CQn+p中的全实2-调和子流形[J].杭州师范大学学报(自然科学版)， 2014，13(5):529-532.

[9] 吴 丹，宋卫东.拟复射影空间CQn+p中的全实伪脐2-调和子流形[J].宁夏大学学报(自然科学版), 2014,35(2):117-119.

[10] 朱 岩，宋卫东.拟复射影空间CQn+p中的全实极小子流形[J].吉林大学学报(理学版)， 2013，51(5)：855-859.

[11] 李海中.关于伪脐子流形的一个整体定理[J].数学杂志,1988,8(2):161-165.

(编辑 HWJ)

The Pseudo-Umbilical Submanifolds with 2-Harmonic in a Quasi-Complex Projective Space

LIUJin-meng1,GENGJie2,SONGWei-dong1*

(1.College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China; 2.Anhui Institute of Information Technology, Wuhu 241000, China)

O186.12

A

1000-2537(2017)05-0080-04

2016-12-24

国家自然科学基金资助项目(11371032);安徽省自然科学基金资助项目(KJ2017A795)

*通讯作者,E-mail：swd56@sina.com

10.7612/j.issn.1000-2537.2017.05.012