历史相依决策模型的建立及相应过程的构造

莫晓云,周杰明，金 芳

(1. 湖南财政经济学院数学与统计学院,中国 长沙 410205；2. 湖南师范大学数学与计算机科学学院，高性能计算与随机信息处理教育部重点实验室,中国 长沙 410081；3.湖南城市学院数学与计算机科学学院，中国 益阳 413000)

历史相依决策模型的建立及相应过程的构造

莫晓云1，2,周杰明2，金 芳3

(1. 湖南财政经济学院数学与统计学院,中国 长沙 410205；2. 湖南师范大学数学与计算机科学学院，高性能计算与随机信息处理教育部重点实验室,中国 长沙 410081；3.湖南城市学院数学与计算机科学学院，中国 益阳 413000)

历史相依决策模型(HDDM)及历史相依决策过程(HDDP)是决策模型及相应的决策过程的一般情形. 马氏决策模型(MDM)及马氏决策过程(MDP)是HDDM及HDDP的特殊情形.本文严格地建立了历史相依决策模型，并证明了相应的历史相依决策过程的存在性，证明是构造性的. 作为HDDM及HDDP的特殊情形，建立了马氏决策模型(MDM), 并构造了相应的马氏决策过程(MDP).

历史相依决策模型的建立; 历史相依决策过程的存在性和构造; 马氏决策模型及马氏决策过程; 马氏过程

AbstractHistory Dependent Decision Model (HDDM) and History Dependent Decision Process (HDDP) are the most general cases of the decision model and their corresponding processes. The Markov Decision Model (MDM) and Markov Decision Process (MDP) are special cases of HDDM and HDDP. In this work, the history dependent decision model has been established, and the existence of corresponding history dependent decision process has been proved. The proof is constructive. As special cases of HDDM and HDDP, the Markov decision model has been established and the Markov decision process has been constructed.

Keywordshistory dependent decision model; Markov decision model; Markov decision process; Markov process

在描述马氏决策模型(MDM)及相应的马氏决策过程(MDP)的决策控制系统中，系统将来的状态只依赖于系统现在的状态和现在采取的决策行动.如果系统将来的状态依赖于系统的历史状态和历史决策行动，这就是历史相依决策模型(HDDM)及相应的历史相依决策过程(HDDP).由于HDDM和HDDP过于一般，较难深入研究.但对马氏决策模型及相应过程，已经有深刻的研究，有丰富的成果[ 1-5 ].关于马氏决策模型及相应过程的诸多专著和论文中，总是简单地提及历史相依决策模型及相应过程，然而却没有详细和准确地给出历史相依决策模型的建立以及相应过程的构造. 因此，完成这个建立和构造很有必要.我们对于诸多相类似的模型及其过程的构造，已经有很好的研究[6-10],本文将利用文献[6-11]中的思想和方法.

1 历史相依决策模型

设有某个受决策者控制的系统，该系统的状态依赖于时间、系统的历史状态和决策者的历史决策行动. 时间可以是连续的，但离散时间更接近于实际的操作. 假定时间为n=0,1,2,…,N.N是正整数，也称期末时. 设在某个时刻，系统处于某个状态x，在该时刻决策者可以作出某个决策行动a，下一时刻，系统的状态将从x转移到某个状态y. 如果在每个时刻n∈{0,1,2,…,N-1}，决策者都做出一个决策行动，这N个行动全体就构成一个决策策略. 策略和行动不同. 研究决策模型的目标之一是选择最好的策略，使得系统的某个指标达到最优.例如，考虑某个投资者，他是决策者，系统的状态就是他的财富，如果他希望期末时财富最多，如何投资就是他的策略.

记系统的状态全体为集合E，称为状态空间. 记决策行动的全体为集合A，称为行动空间. 记R=(-∞,+∞),R+=[0,+∞). 下面从数学上严格地给出历史相依决策模型. 记

H0:=E，

Hn:=Hn-1×A×E,n=1,…,N，

称它们为历史集；元素hn∈Hn具有形式hn=(x0,a0,x1,a1,…,xn-1,an-1,xn),xi∈E,ai∈A.

称hn=(x0,a0,x1,a1,…,xn-1,an-1,xn)为系统至时刻n的历史.

定义1(历史相依决策模型) 给定6元组 (E,A,Dn,Qn,rn,gN),n=0,1,2,…,N-1.

如果它满足下面的(i)至(vi), 称它为历史相依决策模型.

(i) (E,ε)是可测空间，非空集合E称为状态空间，其元素x∈E称为一个状态.

(ii) (A,α)是可测空间，非空集合A称为行动空间，其元素a∈A称为一个行动.

(iii) 可测集Dn⊂Hn×A. 假定：存在一个可测映射fn:Hn→A，使得fn的图{(hn,fn(hn))|hn∈Hn}⊂Dn. 记Dn在hn∈Hn的截口为Dn(hn)={a∈A|(hn,a)∈Dn}. 称元素a∈Dn(hn)为n时刻历史为hn时的一个可取行动，称(hn,a)∈Dn为n时刻的一个历史-行动组合.

(iv)Qn是从Dn到E的一个概率核：

Qn:=Qn(B|hn,a)≡Qn(B|x0,a0,x1,a1,…,xn-1,an-1,xn,a),(hn,a)∈Dn,B∈ε.

固定(hn,a)∈Dn时，Qn(·|hn,a)是(E,ε)上的概率测度. 固定B∈ε时，Qn(B|x0,a0,x1,a1,…,xn-1,an-1,xn,a)是(x0,a0,x1,a1,…,xn-1,an-1,xn,a)的可测函数.

Qn(B|hn,a)表示n时刻历史-行动组合为(hn,a)时，n+1时刻系统的状态处于集合B的概率.Qn描述系统的历史-行动演变的概率规律.

(v) 函数rn:Dn→R，是可测函数.rn(hn,a)表示n时刻历史-行动组合为(hn,a)时，获得的(折现)回报.

(vi)函数gN:HN→R，是可测函数.gN(hN)表示期末N时刻历史为hN时，获得的(折现)回报.

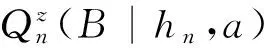
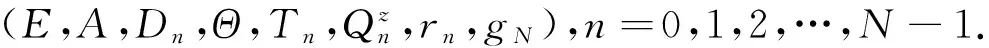
(i)E,A,Dn,rn,gN同定义1.

(ii) (Θ,θ)是可测空间.

(iii)Tn:Dn×Θ→E，是可测映射，称为转移函数或系统函数. 它表示：n时刻的历史-行动组合为(hn,an)，且n+1时刻的干扰为zn+1时，n+1时刻系统的状态将是xn+1=Tn(hn,an,zn+1).

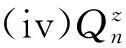
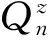
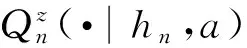
定理1(等价定理) 历史相依决策模型和带干扰的历史相依决策模型是等价的.

证设(E,A,Dn,Qn,rn,gN)是历史相依决策模型. 令

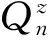
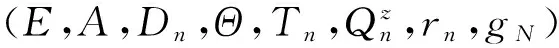
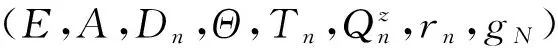
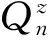
则易验证，(E,A,Dn,Qn,rn,gN)是历史相依决策模型.

定义3(历史相依决策策略) 设(E,A,Dn,Qn,rn,gN)是历史相依决策模型.

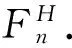
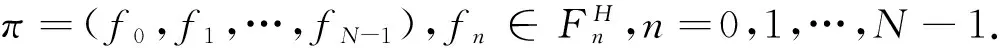
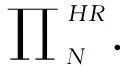
2 历史相依决策过程的存在性和构造

2.1 预备知识

定理2(Tulcea定理[4]) 给定一列可测空间(Ωi,Si),i=0,1,2,…. 记

Xn(ω):=ωn,ω=(ω0,ω1,ω2,…)∈Ω,n=0,1,2,….

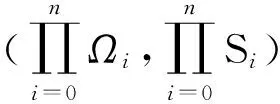
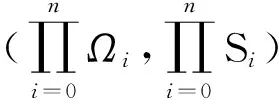
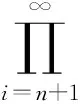
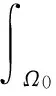
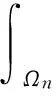
I是示性函数.

从上面的定理，容易得到下面的推论.

推论1给定可测空间(Ωi,Si),i=0,1,2,…,N. 记

Xn(ω):=ωn,ω=(ω0,ω1,…,ωN)∈ΩN,n=0,1,…,N.

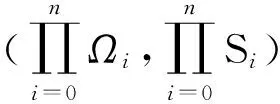
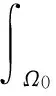
(1)

实际上，只要在定理2中，对i=N,N+1,N+2,…，取

(Ωi+1,Si+1)=(ΩN,SN),P(ω0,…,ωi;dωi+1)=Pi+1(dωi+1),

Pi+1(dωi+1)是(Ωi+1,Si+1)上的任一概率测度即可.

2.2 历史相依决策过程的存在性和构造

下面是历史相依决策过程的存在定理，而且是构造性的.

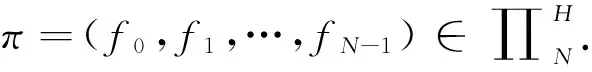
EN+1:=E×E×…×E,εN+1:=ε×ε×…×ε,

Xn(ω):=xn,ω=(x0,x1,…,xN)∈EN+1,n=0,1,…,N.

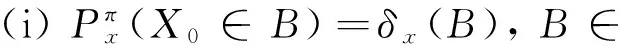
(2)

(3)

称随机过程X={X0,X1,…,XN}为典范历史相依决策过程.

证令

(Ωi,Si):=(E,ε),i=0,1,2,…,N.

(4)

(5)

Xn(ω):=xn,ω=(x0,x1,…,xN)∈EN+1,n=0,1,…,N.

(6)

P0(dx0):=δx(dx0).

(7)

P(x0,x1,…,xn;dxn+1):=Qn(dxn+1|x0,f0(x0),x1,f1(x1),…,xn,fn(xn)),n=1,2,…,N-1.

(8)

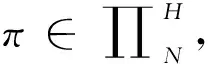
由条件概率乘法公式的积分形式，从上式容易推出，式(2)(3)成立. 定理证完.设

hn=(x0,a0,x1,a1,…,xn-1,an-1,xn)∈Hn.

记条件概率

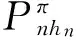
从式(3)，特别地有

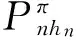
Qn(B|x0,f0(x0),x1,f1(x1),…,xn,fn(xn)).

从上式看出，上式左方的数值与hn=(x0,a0,x1,a1,…,xn-1,an-1,xn)中的a0,a1,…,an-1无关.

3 马氏决策模型和马氏决策过程

所谓马氏决策模型及相应过程，是指历史相依决策模型及相应过程中，对于历史-行动组合(hn,a)∈Dn(hn=(x0,a0,x1,a1,…,xn-1,an-1,x)∈Hn)的相依，实质上只是对于现在的状态-行动组合(x,a)的相依，即马氏相依. 因此，在历史相依决策模型及相应过程中，只要将Hn改成E，将历史hn=(x0,a0,x1,a1,…,xn-1,an-1,x)改成x，就成为马氏决策模型及相应过程. 为明确计，我们给出如下详细定义.

定义5(马氏决策模型) 给定6元组 (E,A,Dn,Qn,rn,gN),n=0,1,2,…,N-1.如果它满足下面的(i)至(v), 称它为马氏决策模型.

(i)E和A同定义1中的(i)(ii).

(ii)可测集Dn⊂E×A. 假定：存在一个可测映射fn:E→A，使得fn的图{(x,fn(x))|x∈E}⊂Dn.对x∈E，记Dn的截口为Dn(x)={a∈A|(x,a)∈Dn}.称元素a∈Dn(x)为n时刻状态为x时的一个可取行动，(x,a)称为一个状态-行动组合.

(iii)Qn:=Qn(B|x,a)是从Dn到E的一个概率核. 固定(x,a)∈Dn时，Qn(·|x,a)是(E,ε)上的概率测度. 固定B∈ε时，Qn(B|x,a)是(x,a)的可测函数.Qn(B|x,a)表示n时刻状态-行动组合为(x,a)时，n+1时刻的状态处于集合B的概率.

(iv)函数rn:Dn→R，是可测函数.rn(x,a)表示：n时刻的状态-行动组合为(x,a)时，获得的(折现)回报.

(v)函数gN:E→R，是可测函数.gN(x)表示在N时刻(期末时)状态为x时，获得的(折现)回报.

如果rn(x,a):=βnr(x,a),gN(x):=βNg(x)，β∈(0,1]是某个(折现)因子，称马氏决策模型为平稳的.

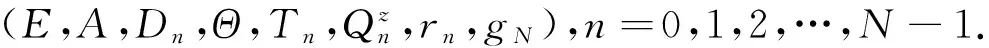
(i)E,A,Dn,rn,gN同定义5.

(ii) (Θ,θ)是可测空间.

(iii)Tn:Dn×Θ→E是可测映射，称为转移函数或系统函数. 它表示：n时刻的状态-行动组合为(x,a)，且n+1时刻的干扰为zn+1时，n+1时刻的状态将是xn+1=Tn(x,a,zn+1).

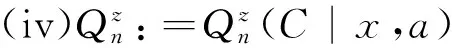
定理4(等价定理)马氏决策模型和带干扰的马氏决策模型是等价的.

定理4的证明类似定理1的证明，略.

定义7(马氏决策规则和马氏决策策略) 设(E,A,Dn,Qn,rn,gN)是马氏决策模型.

(i) 固定n∈{0,1,…,N-1}. 一个可测映射fn:E→A，使得fn(x)∈Dn(x),∀x∈E，称fn为n时刻的一个马氏决策规则.n时刻的马氏决策规则fn全体记为Fn.

(ii) 设π=(f0,f1,…,fN-1),fn∈Fn,n=0,1,…,N-1. 称π为一个N阶段马氏决策策略，其全体记为∏N.

下面的定理是定理3 的特殊情形.

定理5(典范马氏决策过程的存在性和构造) 给定马氏决策模型 (E,A,Dn,Qn,rn,gN),n=0,1,2,…,N-1.x∈E，π=(f0,f1,…,fN-1)∈∏N. 令

Xn(ω)=xn,ω=(x0,x1,…,xN)∈EN+1,n=0,1,…,N.

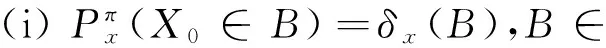
(9)

(10)

称X=(X0,X1,…,XN)为马氏决策过程. 它是马氏过程.

从式(10)的第1等式看出，马氏决策过程X=(X0,X1,…,XN)是马氏过程，它具有马氏性. 从第2等式看出，它在n时刻的一步转移概率记为Pn(x,B),x∈E,B∈ε，则Pn(x,B)=Qn(B|x,fn(x)).

4 期望总回报目标函数和值函数

4.1 历史相依决策过程情形

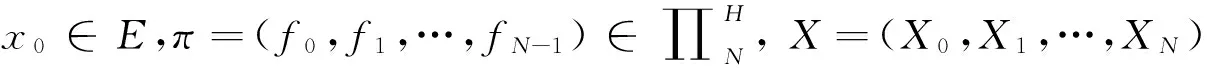
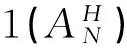
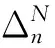
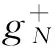
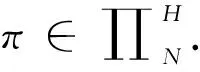
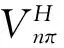
gN(X0,f0(X0),…,XN-1,fN-1(XN-1),XN)].

为策略π时在[n,N]时段的期望总回报. 称

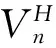
为在[n,N]时段的值函数.

4.2 马氏决策过程情形

可积性假设2(AN) 对n=0,…,N, 假定

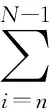
设π∈∏N. 称

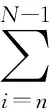
为策略π时在[n,N]时段的期望总回报. 称

Vn(x):=supπ∈∏NVnπ(x),x∈E

为在[n,N]时段的值函数.

定理6[1，4]对n=0,1,…,N-1, 如果hn=(x0,a0,x1,a1,…,xn-1,an-1,xn)∈Hn，则

即

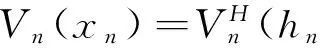
定理6说明，对于历史相依决策过程，如果仅仅只研究其值函数，则只要研究马氏决策过程.

致谢感谢“风险理论与随机控制”讨论班的老师们提出的研究问题和宝贵建议.

[1] BAUERLE N, RIEDER U. Markov decision processes with applications to finance [M]. Berlin: Springer-Verlag, 2011.

[2] GUO X P, HEMANDEZ-LEMA O. Continuous-time Markov decision processes [M]. Berlin: Springer-Verlag, 2009.

[3] GUO X P, HEMANDEZ-LEMA O, PRIETO-RUMEAU T. A survey of recent results on continuous-time Markov decision processes [J]. Top, 2006,14(2):177-246.

[4] HINDERER K. Foundations of non-stationary dynamic programming with discrete time parameter [M]. Berlin: Springer-Verlag, 1970.

[5] 严加安. 测度论讲义(第二版)[M]. 北京：科学出版社，2004.

[6] 莫晓云. 用独立乘积空间构造相依随机变量的组装法 [J]. 湖南师范大学自然科学学报, 2010,33(2)：3-6.

[7] 莫晓云，欧 辉，周杰明. Markov相依风险模型的等价定理及概率构造 [J]. 经济数学， 2012,29(1)：61-64.

[8] MO X Y，YANG X Q. Criterion of semi-Markov dependent risk model [J]. Acta Math Sin, 2014,30B(7):1237-1280.

[9] MO X Y，ZHOU J M, OU H,etal. Double Markov risk model [J]. Acta Math Sci, 2013,33B(2):330-340.

[10] 莫晓云，杨向群. Markov调制风险模型的轨道刻划和概率构造[J]. 应用数学学报， 2012,35(3):385-394.

[11] ZHOU J M， MO X Y， OU H,etal. Expected present value of total dividends in the compound binomial model with delayed claims and random income[J]. Acta Math Sci, 2013,33B(6):1639-1651.

(编辑 HWJ)

Establishment of History Dependent Decision Models and Construction of Corresponding Processes

MOXiao-yun1,2,ZHOUJie-ming2,JINFang3*

(1. College of Mathematics and Statistics, Hunan University of Finance and Economics, Changsha 410205, China； 2. College of Mathematics and Computer Science, Key Laboratory of High Performance Computing and Stochastic Information Processing, Ministry of Education of China, Hunan Normal University, Changsha, 410081, China； 3.College of Mathematics and Computing Science, Hunan City University, Yiyang, 413000, China)

O212.5

A

1000-2537(2017)05-0088-07

2016-12-05

国家自然科学基金资助项目(11671132，11601147，11626094)；湖南省哲学社会科学研究资助项目(16YBA053 )；湖南省教育厅重点科研资助项目(15A032)； 湖南省教育厅科研资助项目(16C0953，16C0296)；湖南省自然科学基金资助项目(2017JJ3206)

*通讯作者,E-mail：moxyun72@163.com

10.7612/j.issn.1000-2537.2017.05.014