T-凸空间中的KKM引理及其应用

2017-10-14陈治友

湖南师范大学自然科学学报 2017年5期

关键词：凸性标号线性

陈治友

(贵阳学院数学与信息科学学院，中国贵阳 550005)

T-凸空间中的KKM引理及其应用

陈治友

(贵阳学院数学与信息科学学院，中国贵阳 550005)

空间的凸性在非线性分析理论、变分不等式论以及最优化理论等领域扮演着重要角色.在这些领域中，不论是理论方面的问题，还是应用方面的问题，都依赖于空间的凸性.然而很多空间都不具备通常的以线性结构为基础的“凸性”.在不具有线性结构的空间中，建立广义凸性，同时把连续选择定理、不动点定理以及其他重要结果推广到不依赖线性结构的广义凸性空间中具有十分重要的意义.为此，充分利用T-凸空间所满足的H0-条件和经典的分析方法，在不具有线性结构的T-凸空间中，建立并证明KKM引理；同时借助该引理，给出一个不动点定理和一个不具拟T-凹性的函数的一个Ky Fan不等式的解的存在性定理．

T-凸空间；H0-条件；KKM引理；Ky Fan不等式

AbstractConvexity of spaces plays a very important role in non-linear analysis theory, variational inequality theory, optimal theory and so on. In all these cases of theoretical and applied studies, the dependence on the convexity of spaces is presumed. However, a lot of spaces do not possess the convex property from the viewpoint of the usual linear structure. Because of this, it has become recent interest to establish generalized convexity on spaces without linear structure and to generalize the continuity selection theorem, the fixed point theorem and some other important results, to generalized convex spaces. Here we make full use of theH0-condition ofT-convex space and classical analysis method, to prove KKM lemma onT-convex space without linear structure. Finally, we study two applications of this lemma onT-convex space. One is the fixed point theorem and the other is the existence theorem for the solution of Ky Fan inequality without quasi-T-concavity onT-convex spaces.

KeywordsT-convex space;H0- condition; KKM lemma; Ky Fan inequality

文献[1]用集合的可缩性构造集合族，利用该集合族定义了一种广义凸性，据此定义了具有H-凸结构的H-空间，该空间将先前的线性凸结构进行了推广.文献[2]指出任何Hausdoff拓扑线性空间，凸空间，可缩空间，伪凸空间都是H-空间.而后，一些专家学者研究了一般拓扑空间中的凸结构，如：半格凸、G-凸、B-凸、Van de Vel凸、Michael-凸、L-凸、超凸等．文献[3-4]指出上述一系列凸结构有一个共性特征，即都满足H0-条件.文献[5]利用连续映射的延拓性质构造了具有T-凸结构的T-凸空间，该空间的T-凸性是H-空间的H-凸性的推广.并且还证明了T-凸空间满足H0-条件.文献[6-11]将一些线性拓扑空间中的重要结果推广到不依赖线性结构的广义抽象凸空间中做了重要尝试.本文将在这些研究的基础上，充分利用T-凸空间所满足的H0-条件和经典的分析方法，在不具有线性结构的T-凸空间中，建立并证明KKM引理；同时借助该引理，证明一个不动点定理和一个不具拟T-凹性的函数的一个Ky Fan不等式的解的存在性定理．

1 预备知识

定义1[5]设X,Y为拓扑空间，A⊂X为X的任意子集，f:A→Y连续，若存在连续映射f*:X→Y，使得f*(x)=f(x),∀x∈A，则称f可以从A延拓(或扩张)X．

定义2[5]设X,Y为拓扑空间，若对X的任意子集A⊂X及任意连续映射f:A→Y，f可以从A延拓X，则称Y关于X具有延拓性质．

定义3[5]设X为一拓扑空间，定义集族{TA}为TA={D⊂X:D关于X具有延拓性质}．以X中一切有限子集A编号，且当A⊂B时，TA⊂TB，则称二元对(X,{TA})为一T-凸空间．集D⊂X称为T-凸的，如果对任意有限集A⊂D，都有TA⊂D．

设(X,{TA})是一T-凸空间，定义A⊂X的T-凸包为：coTA=∩{D⊂X:A⊂D且D是T-凸的}．

易验证，若A⊂X为T-凸当且仅当coTA=A．

定义4[5]称T-凸空间(X,{TA})满足H0-条件，如果凸结构{TA}有下面性质：

对每个有限集{x0,x1,…,xn}⊂X，存在连续映射

f:ΔN→coT{x0,x1,…,xn}

使得

f(ΔJ)⊂coT{xj:j∈J}，∀φ≠J⊂N．

其中ΔN=e0e1…en是n维标准单纯形，e0,e1,…,en是Rn+1中的标准正交基．

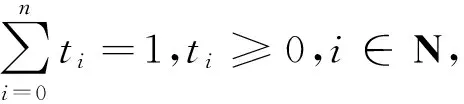
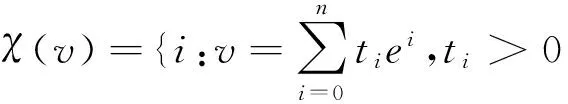
定义5设{Ti:i∈I}是n维标准单纯形ΔN=e0e1…en的一类单形剖分，υ表示该类单形剖分的所有子单形的所有顶点的集.若函数λ:υ→{0,1,…,n}满足：

λ(v)∈χ(v),∀v∈υ，

则称该函数为这个剖分的一个正常标号.进而，若Ti的顶点对应一个完全标号集{0,1,…,n}，则称Ti是一个具有完全标号的子单形.

引理1[4]设{Ti:i∈I}是n维标准单纯形ΔN=e0e1…en的任意一单形剖分，并且被函数λ进行正常标号，则在这一剖分中一定存在奇数个具有完全标号的子单形.

注3: 设Y是一个T-凸Hausdorff拓扑空间，X是Y的一个非空闭T-凸集，若泛函ψ：X×X→R满足：对任一λ∈R,集合

Fλ={y∈X:-ψ(x,y)≤λ,∀x∈X}

是T-凸的，则称∀x∈X,ψ(x,y)在X上关于y是拟T-凹的．

2 主要结果

证设{y0,y1,…,yn}是X的任一有限子集.由于(Y,{TA})是一T-凸空间，因此，它满足H0-条件，所以必存在一单值的连续函数

使得对每一个非空子集J⊂N,有

f(ΔJ)⊂coT{y0,y1,…,yn}.

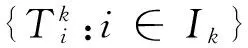
对每一个v∈υk，令

λk(v)=min{j∈χ(v):f(v)∈F(yj)}.

由假设，因为v∈coT{ej:j∈χ(v)}且

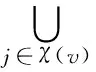
则λk(v)是非空的.易知λk是这个剖分的一个正常标号函数.

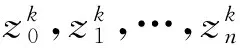
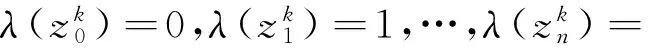
由λ的定义，有

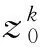
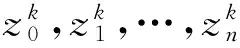
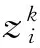
由于ΔN是紧的，因此必存在y*∈ΔN，使得

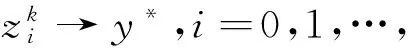
则

又因为F为闭值的，即有每一个F(yi),i=0,1,…,n是闭的，故

f(y*)∈F(yi),i=0,1,…,n.

即

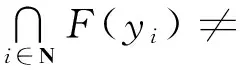
定理1得证.

3 应用

证由于X紧，且开集族{F-1(x):x∈X}覆盖X，据有限覆盖定理，必存在X的有限子集{x0,x1,…,xn}，使得有限个开集的集：

{F-1(xi):xi∈X,i=0,1,…,n}，

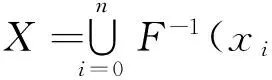
H(x)=[XF-1(x)],x∈X.

易知H是闭的，据定理1，H不是KKM映射.因此必存在有限子集

{y0,y1,…,ym}⊂X,

使得

即存在某个y*∈coT{y0,y1,…,ym}，使得y*∉H(yi),i=0,1,…,m.即

y*∈F-1(yi),∀i=0,1,…,m.

从而有

yi∈F(y*),∀i=0,1,…,m.

因此有

y*∈coT{y0,y1,…,ym}⊂F(y*).

定理2得证.

定理3设Y是一个T-凸Hausdorff拓扑空间，X是Y的一个非空闭T-凸集，设泛函φ和ψ是X×X→R的且满足条件：

(1)φ(x,y)≤ψ(x,y),ψ(x,x)≤0,∀x,y∈X；

(3)∀x∈X,ψ(x,y)在X上关于y是拟T-凹的．

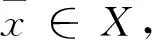
证作映射G,H:X→2X分别如下：

G(y)={x∈X:φ(x,y)≤0},H(y)={x∈X:ψ(x,y)≤0}．

由(2)知下水平集G(y)闭．下证G为KKM映射．即证：

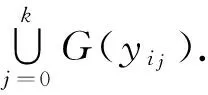
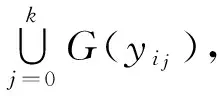
于是由(1)就有ψ(u,yj)>0,j=i0,…,ik，再由(3)有ψ(u,u)>0与(1)矛盾，故

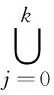
定理3得证.

[1] HORVATH C D. Some results on multivalued mappings and inequalities without convexity[M]. in: Lin B.L., Simons S.(Eds.), Nonlinear and Convex Analysis, Marcel Dekker, 1987.

[2] BARDARO C, CEPPITELLI R. Some futher generalizations of Knaster-Kuratowski-Mazurkiewicz theorem and minimax inequalities[J].J Math Anal Appl, 1988,132(3):484-490.

[3] XIANG S W, YANG H. Some properties of abstract convexity structures on topological spaces[J]. Nonlinear Anal, 2007,67(5):803-808.

[4] XIANG S W, XIA S Y. A further characteristic of abstract convexity structures on topological spaces[J].J Math Anal Appl, 2007,335(7)：716-723.

[5] 陈治友.T-凸空间的结构和性质[J].西南大学学报(自然科学版)， 2012,34(10)：106-108.

[6] 陈治友，夏顺友.抽象凸空间中广义最大元的稳定性[J].西南大学学报(自然科学版)，2012,34(8)：116-118.

[7] 陈治友，夏顺友.抽象凸空间上广义博弈Nash平衡点的存在性[J].辽宁工程技术大学学报(自然科学版)，2012,31(5)：786-791.

[8] 夏顺友.抽象凸空间上弱Ky Fan点的存在性及其等价描述[J]. 辽宁工程技术大学学报(自然科学版)，2013,32(10)：1437-1440.

[9 ] 夏顺友. 集值Sperner组合引理与抽象凸空间中的KKMS引理[J]. 西南师范大学学报(自然科学版)，2013,38(6):25-29.

[10] 陈治友，夏顺友.抽象凸空间中的Shapley-KKM引理[J].四川师范大学学报(自然科学版)，2014，37(3)：338-340.

[11] 夏顺友. 抽象凸空间上的拟变分不等式及其应用[J]. 应用数学学报， 2014,37(1)：78-86.

(编辑 HWJ)

KKM Lemma and Its Applications onT-Convex Spaces

CHENZhi-you*