不规则波与开孔沉箱相互作用数值模拟

唐 蔚，孙大鹏，吴 浩

(大连理工大学 海岸及近海工程国家重点实验室，辽宁 大连 116024)

不规则波与开孔沉箱相互作用数值模拟

唐 蔚，孙大鹏，吴 浩

(大连理工大学 海岸及近海工程国家重点实验室，辽宁 大连 116024)

采用三步有限元法对N-S方程进行离散，同时借助CLEAR-VOF方法追踪流体自由表面，利用主动吸收式造波等手段改进了二维不规则波浪数值水槽，使得水槽中的波浪谱与目标靶谱吻合较好。进而建立了不规则波浪与开孔沉箱作用一种新的数值模式，分析研究不规则波作用下开孔沉箱的反射率，并与现有的物模结果和数模结果进行了对比，为不规则波与开孔沉箱作用问题的研究，探求了一种新的数值手段。

不规则波；CLEAR-VOF方法；主动吸收式造波；开孔沉箱；反射率

Abstract: A two-dimensional irregular wave numerical flume is established by active absorption wave-maker. In this numerical model, the three step finite element method is used to discrete N-S equation, and the CLEAR-VOF method is used to track the free surface of the fluid. The wave spectrum in the flume is in good agreement with the target spectrum. And then a new numerical model of irregular wave acting on perforated caisson is put forward. The reflection coefficient of perforated caisson is studied, and compared with the existing results of the physical model and numerical results, and finally a new numerical research method is explored for irregular waves acting on perforated caisson.

Keywords: irregular wave; CLEAR-VOF; active absorbing wave-maker; perforated caisson; reflection coefficient

自从Jarlan[1]提出开孔沉箱型式的防波堤之后，国内外许多学者对其水动力特性进行了大量的研究。研究发现，开孔沉箱结构能有效减少沉箱前的波浪反射并且降低结构受力，因而在工程中得到广泛的应用。陈雪峰等[2]通过物理模型试验，分析研究了波浪反射率与开孔板的开孔率、消浪室相对宽度等影响因素之间的关系；周凌愉和戴路[3]通过波浪断面试验讨论不规则波浪作用下开孔沉箱消浪效果与消浪室、水深、波高、码头面超高、开孔率等影响因素的关系，得到开孔沉箱码头反射系数的简化公式。Suh[4-5]等利用伽辽金特征函数法提出了计算不规则波浪作用下单层开孔沉箱反射系数的方法，并与物模实验结果进行了对比,研究发现波浪的频率对不规则波反射有直接影响；刘勇等[6]基于线性势流理论并利用匹配特征函数展开法建立了不规则波浪与开孔沉箱相互作用的模型来分析沉箱的受力特点。迄今，对于不规则波浪与开孔沉箱相互作用的研究多集中在物模试验方面，但相应的数值模拟研究成果却鲜见报道。考虑到实际工程中的波况都是不规则波浪，而物模试验成果是相对有限的，为了拓宽研究范围并使成果便于工程设计应用，开展不规则波浪与开孔沉箱作用数值模式的研究是必要的。

1 数值方法

1.1控制方程及其离散

采用二维黏性不可压缩流体的连续性方程和Naiver-Stokes方程为基本控制方程，引入大涡模拟方法模拟湍流效应，其控制方程为：

上式中所有物理量均为滤去脉动之后的平均量，其中：p为压强；u为流速；ρ为流体密度；f为作用在流体上的体积力；υe表示有效黏性系数，υe=υ+υt，υ为湍流黏性系数，υt为运动黏性系数；下标i和j表示方向。

对控制方程的离散采用能有效处理复杂开孔边界形态并且数值实现相对简单的三步有限元法[7]，将每个时间步分成三个小步来完成，可以得到展开的的Navier-Stokes方程离散形式：

关于压力p的泊松方程如式(6)所示：

最后再采用传统的Galerkin加权余量法对上述各式进行求解。

1.2自由表面追踪

图1 流体多边形的输运示意Fig. 1 Sketch of motion of fluid polygon

早期的VOF方法提出了一个流体体积函数，将每个网格单元内部流体所占有体积与该单元可容纳流体体积之比定义为流体F函数。而CLEAR-VOF方法则与其不同，它是由Ashgriz等[8]于2004年提出的适用于非结构化网格的自由表面重构方法，该方法精度高并且完善了经典的VOF方法，通过在欧拉网格基础上采用拉格朗日思想和计算几何学方法来实现F函数的更新。

图1中的粗线表示某时刻t的水体自由表面，细线表示计算网格线。计算出流场内网格节点的速度之后，网格边线上任意点速度可以由相邻网格节点速度通过插值求出。图1显示了经过Δt时间，流体多边形abcd变为流体多边形a’b’c’d’的过程，部分流体会由母单元向其他周围单元输运。在确定流体多边形每个顶点在新时刻的位置之后，通过计算几何学方法，就能得到t+Δt时刻下的各单元的VOF函数值，进而得到水体自由表面。

2 数值波浪水槽的建立

2.1主动吸收式造波

通常在进行不规则波与建筑物相互作用的数值模拟时，需要模拟的造波时间较长，波浪会在建筑物与造波板之间多次来回反射，将严重影响模拟区域内产生的波浪特性以及模拟精度，使数值模拟难以进行。

为了消除造波端的二次反射波，采用Frigaard和Christensen[9]提出的主动吸收式造波方法进行造波。该方法原理如下：在波浪水槽中加入两个浪高仪作为滤波器，实时采集波高数据，通过一系列滤波变换分离出入射波和反射波信号，并将反射波信号作为修正信号反馈到造波端，吸收掉不规则波中反射波的部分，最终达到消除二次反射的目的。

不规则波频率区间划分采用等分能量法，造波板运动速度：

其中，ηp-j表示(p-j)·Δt时刻放置滤波器处实时波面数据；X*p表示p·Δt时刻得到的造波修正信号；N表示滤波器数组大小；hj表示t=j·Δt时刻的滤波系数；Δt表示滤波器的采集时间间隔。

2.2数值波浪水槽的性能验证

2.2.1 造波有效性验证

为验证造波端的主动吸收功能，将水槽右端设置为直墙边界并进行造波。理论上，如果造波端没有二次反射波浪，入、反射波分离之后，水槽中的波浪入射谱应与靶谱相一致。

图2 数值波浪水槽中不规则波入射谱与靶谱的对比Fig. 2 Comparison of incident spectrum and target spectrum of irregular waves in a numerical wave flume

由图2可以看出，数值波浪水槽中不规则波入射谱与靶谱的能量分布、峰频位置以及频率分布等特征均吻合良好。

2.2.2 造波稳定性验证

当数值水槽右端设置为直墙时，若水槽造波端不具有吸收功能，波浪将在水槽中多次反射叠加，导致波高会越来越大，直至计算发散。为验证数值水槽的造波稳定性，将数值模拟的造波时间加长，观察波面是否稳定，并比对入射谱与靶谱。图3给出了造波时间为T=230 s，距离造波端1.8 m与7.0 m两位置处的入射谱与目标靶谱的对比。

由图3可以看出，经过较长时间的造波，得到的频谱基本与靶谱吻合，并且沿水槽长度方向不同位置处的入射谱也与靶谱吻合较好，说明所采用的造波方法能够在数值波浪水槽中生成稳定的不规则波浪。

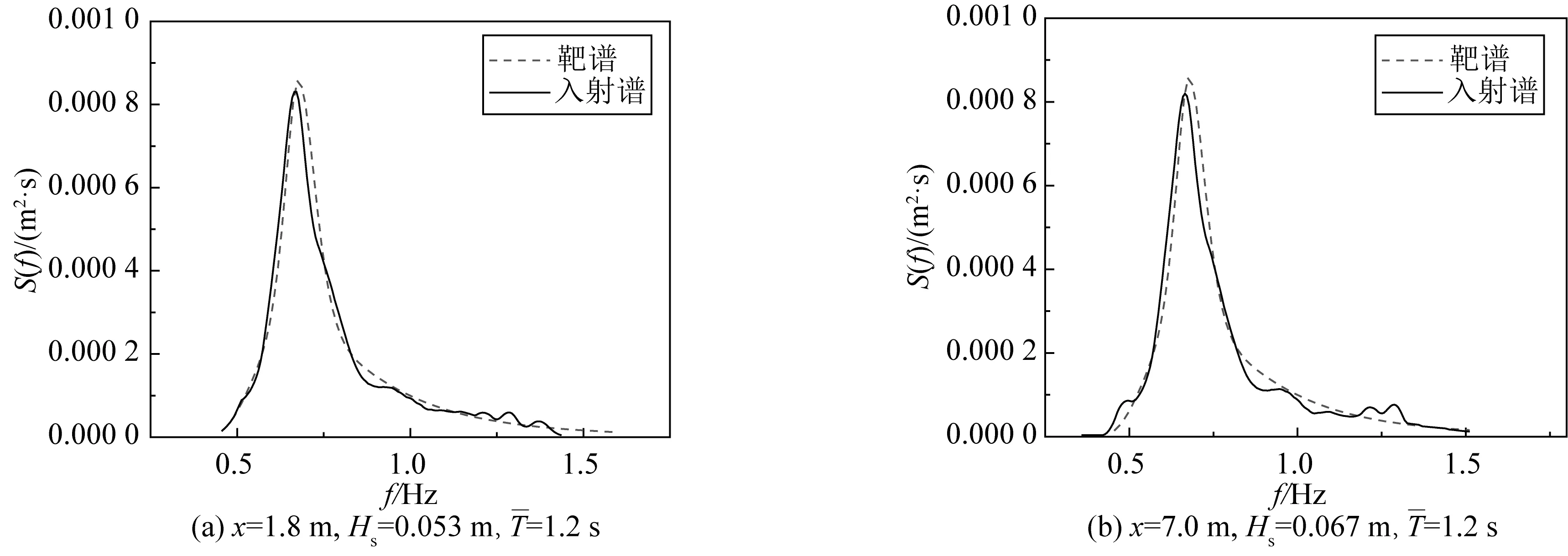
图3 数值水槽不同位置处的入射谱与靶谱的对比Fig. 3 Comparison of the incident spectrum and the target spectrum at different locations of the numerical flume

3 数值计算结果及分析

3.1开孔沉箱在数值波浪水槽的布置

数值波浪水槽示意如图4所示，水槽试验段长7.7 m、高0.6 m，数模试验中水深保持0.4 m不变。水槽左端为主动吸收式造波边界，水槽试验段内安放开孔沉箱，水槽底部、开孔板的非开孔部分以及消浪室后墙设置为固体边壁。

图4 数值水槽布置示意Fig. 4 Sketch of the numerical flume

图5 开孔板开孔位置示意Fig. 5 The shape of perforated caisson orifice

开孔板的开孔率分20%和40%两种，具体尺寸如图5所示。当开孔率α=20%时，每个孔尺寸为高0.032 m、宽0.142 m；当开孔率为40%时，孔高为0.064 m、宽0.142 m。

3.2波浪与开孔沉箱作用的波况对比

本课题的研究过程中，已先期开展了不规则波浪与开孔沉箱相互作用的物模试验[10]，参照图4所示开孔沉箱前的浪高仪布置，2#浪高仪位置处数值模拟和物模试验得到的波面历时曲线对比示例如图6所示，统计分析其有效波高与周期并做对比如表1所示，进而分析给出该位置处的数值水槽频谱与物模试验的频谱对比如图7所示。

由表1可以看出，在数值水槽中加入开孔沉箱之后，数值模拟得到不规则波的有效波高和周期与物模结果近乎一致；图7中数模的频谱与物模试验频谱的能量分布、峰频位置以及频率分布等均吻合良好。

图6 2#浪高仪位置处数值模拟和物模试验的波面历时曲线对比Fig. 6 Time series of wave elevation at gauge 2 in front of caisson

图7 开孔沉箱前2#浪高仪位置处的数值水槽频谱与物模频谱对比Fig. 7 Spectrum comparison between simulated results and physical model at gauge 2 in front of caisson

试验工况物模值本文数模值入射波高Hs/m周期T-/s沉箱前波高Hs/m周期T-/s沉箱前波高Hs/m周期T-/s0．0531．00．0601．00．0611．00．0671．20．0711．20．0721．2

3.3波浪与开孔沉箱作用反射率数值模拟结果

工程中通常用波浪的反射率来评价开孔沉箱的消浪效果，现行《防波堤设计与施工规范》[11]中，给出了不规则波作用下的开孔沉箱反射系数的计算公式为：

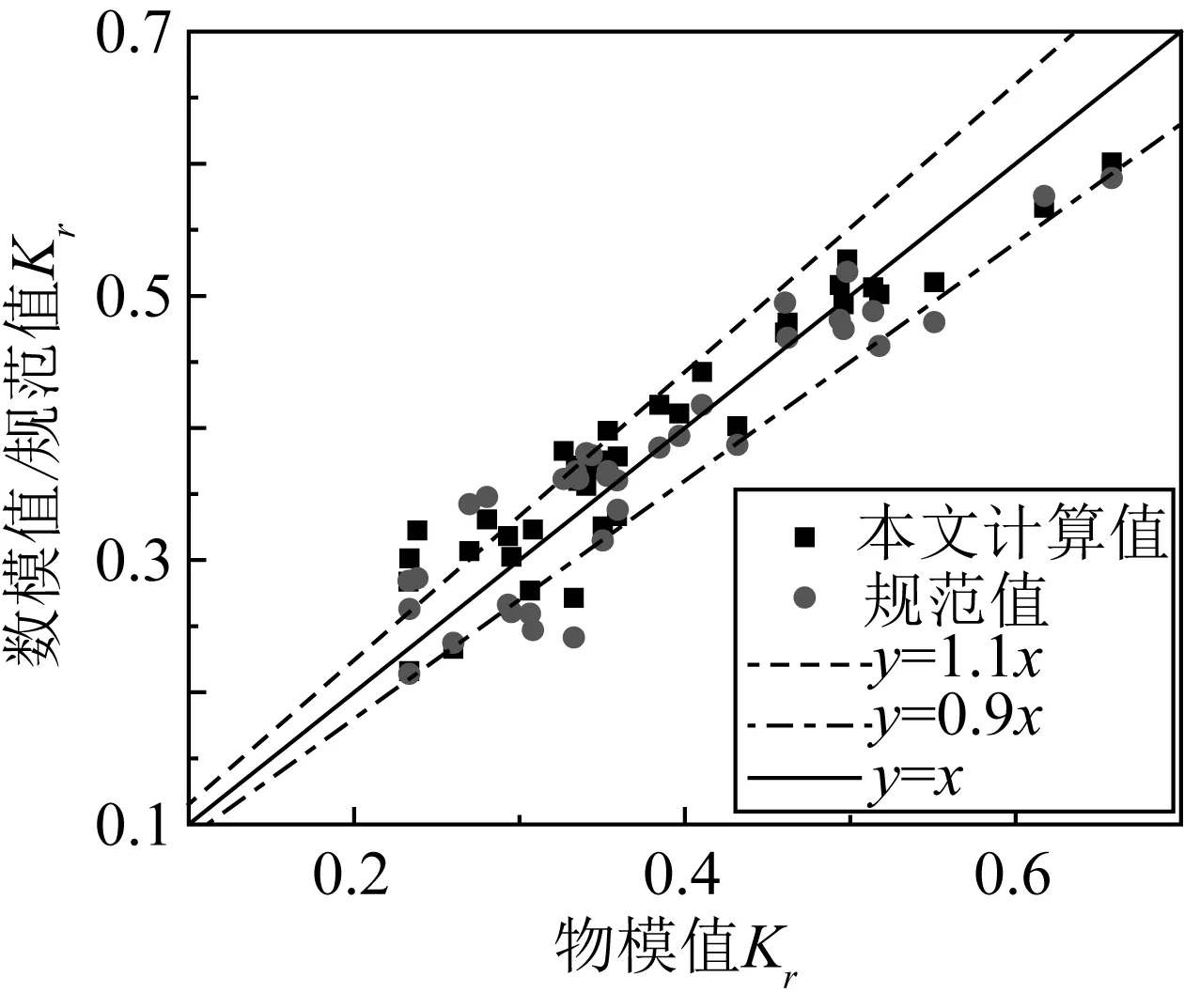
图8 数模值以及规范值与物模值的比较Fig. 8 Comparison of Kr between numerical results, norm value and physical experiment value

式中：α为开孔率。

为了验证本文所研究的不规则波浪与开孔沉箱相互作用的正确性与有效性，将本文的数值模拟计算结果、式(9)的规范计算值与物模试验的结果进行对比，如图8所示。图中的实、虚线分别代表y=x以及y=x(1±10%)，横坐标表示物模试验的结果，纵坐标表示本文数模结果与规范计算值。其中，方形点表示本文数值模拟值，圆形点表示规范计算值。可以看出，本次数值模拟大部分数据点都分布在两条虚线以内。

以物模试验值为基准，表2给出了开孔沉箱前波浪反射率的规范值、本文数模计算值、陈雪峰数模计算值[10]与物模值的比较。

表2 开孔沉箱前波浪反射率的规范值、本文数模计算值、陈雪峰数模计算值与物模值的比较Tab. 2 Comparison of Kr between numerical results, norm value and physical experiment value in front of caisson

从表2可以看出，本文反射率的数值结果与规范值相比，与物模试验结果吻合得更好；相同计算工况下，本文反射率的数值结果和陈雪峰数模计算值[10]相比，与物模试验结果的误差更小。

综合3.2和3.3开孔沉箱前波况、反射系数数模和物模研究结果的对比分析，表明数值波浪水槽对开孔沉箱前的波况模拟具有较高的计算精度。

3.4开孔沉箱反射率影响因素

采用单因次分析法，分别考察消浪室相对宽度B/L、相对水深d/L、相对波高Hs/L各因素对反射系数Kr的影响，并与相同工况下的物模试验值、式(9)规范值进行对比，探求开孔沉箱反射系数主要影响因素的规律性。

1)考察消浪室相对宽度B/L对反射系数Kr的影响

图9 B/L与Kr之间的关系Fig. 9 Relational graph of B/L versus Kr

从图9可以得出，在Hs=0.053 m、0.067 m，消浪室宽度B=0.15 m、0.2 m、0.3 m，开孔率α=0.2、0.4时，相对于规范值，本文数模结果更贴近于物模试验值。物模试验和数值模拟的结果都表明：开孔沉箱的不规则波反射系数和消浪室相对宽度呈非线性关系，且当B/L取到0.18左右时，反射系数Kr有最小值。

2)考察相对水深d/L对反射系数Kr的影响

从图10可以得出，在Hs=0.053 m、0.067 m，消浪室宽度B=0.15 m、0.2 m，开孔率α=0.2、0.4时，数模计算值、物模试验值和规范值三者趋势相同，且数模计算值和物模试验值吻合良好，即随着相对水深d/L的增大，开孔沉箱的反射系数Kr呈现递减趋势，并且两者之间大致呈线性相关关系。

图10 d/L与Kr之间的关系Fig. 10 Relational graph of d/L versus Kr

3)考察相对波高Hs/L对反射系数Kr的影响

从图11可以得出在Hs=0.053 m、0.067 m，开孔率α=0.2、0.4，消浪室宽度B=0.15 m、0.2 m时，数模计算值、物模试验值和规范值三者规律性大体相同，且数模计算值和物模试验值的吻合程度相对较好，即开孔沉箱的反射率随着相对波高Hs/L的增大而减小，并且两者之间大致呈线性相关关系。

图11 Hs/L与Kr之间的关系Fig. 11 Relational graph of Hs/L versus Kr

由本节讨论可以得出：不规则波与开孔沉箱作用的反射率Kr的主要影响因素为相对消浪室宽度B/L、相对水深d/L和相对波高Hs/L；反射率Kr与相对消浪室宽度B/L呈非线性相关关系，且Kr在B/L取得0.18左右时有最小值。反射率Kr与相对水深d/L和相对波高Hs/L大致呈线性相关关系，Kr随着这两个量的增大而相应减少。

4 结 语

基于N-S方程，将三步有限元法与CLEAR-VOF相结合，通过主动吸收式造波消除造波端的二次反射波浪，改进了不规则波浪数值水槽，进而成功实现了不规则波浪与开孔沉箱相互作用的波况模拟。本文的数值结果与物模试验结果吻合较好，且计算精度优于规范值和已有的数模结果。表明：本文所建立的不规则波浪与开孔沉箱作用新的数值模式，具有较好的适定性和较高的计算精度，为本课题的深入研究奠定了可靠的数模基础，成果对开孔沉箱的工程设计应用具有参考和借鉴意义。

[1] JARLAN G E. A perforated vertical wall breakwater[J]. The Dock and Harbour Authority, 1961, 41(486): 394-398.

[2] 陈雪峰, 李玉成, 孙大鹏. 不规则波与开孔沉箱相互作用的实验研究[C]//第八届全国海洋工程学术会议. 2000: 262-269. (CHEN Xuefeng, LI Yucheng, SUN Dapeng. Experimental investigation of irregular waves acting on perforated caisson [C]//Proceedings of the Eighth National Conference on Marine Engineering. 2000: 262-269.(in Chinese))

[3] 周凌愉, 戴路. 不规则波作用下开孔沉箱结构码头反射系数研究[J]. 中国水运(下半月), 2012(6): 253-255. (ZHOU Lingyu, DAI Lu. Study on reflection coefficient of perforated caisson structure wharf under irregular wave [J]. China Water Transport, 2012(6): 253-255. (in Chinese))

[4] SUH K D, CHOI J C, KIM B H, et al. Reflection of irregular waves from perforated wall caisson breakwaters [J]. Coastal Engineering, 2001, 44: 141-151.

[5] SUH K D, PARK J K, PARK W S. Wave reflection from partially perforated-wall caisson breakwater [J]. Ocean Engineering, 2006, 33(2): 264-280.

[6] LIU Yong, LI Yucheng, TENG Bin, et al. Total horizontal and vertical forces of irregular waves on partially perforated caisson breakwaters [J]. Coastal Engineering, 2008, 55: 537-552.

[7] 吕林, 李玉成, 陈兵. 溃坝流动的有限元数值模拟[J]. 中国造船, 2006, 46(B11): 246-252. (LV Lin, LI Yucheng, CHEN Bing. Numerical simulation of dam breaking with finite element method [J]. Shipbuilding of China, 2006, 46(B11): 246-252. (in Chinese))

[8] ASHGRIZ N, BARBAT T, WANG G. A computational lagrangian-eulerian advection remap for free surface flows [J]. International Journal for Numerical Methods in Fluids, 2004, 44(1):1-32.

[9] FRIGAARD P, CHRISTENSEN M. An absorbing wave-maker based on digital filters [J]. Coastal Engineering, 2012:168-180.

[10] 陈雪峰. 波浪与开孔沉箱的相互作用[D]. 大连: 大连理工大学, 2003. (CHEN Xuefeng. Wave interaction with perforated caisson breakwaters [D]. Dalian: Dalian University of Science and Technology, 2003. (in Chinese))

[11] JTS154-1-2011, 防波堤设计与施工规范[S].中华人民共和国交通部发布, 2011. (JTS154-1-2011, Code of design and construction of breakwaters [S]. 2011. (in Chinese))

Numerical investigation of perforated caisson under the action of irregular wave

TANG Wei, SUN Dapeng, WU Hao

(State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China)

TV139.2

A

10.16483/j.issn.1005-9865.2017.04.006

1005-9865(2017)04-0044-09

2016-12-17

国家自然科学基金资助项目(51279027；51221961)

唐 蔚(1992-)，男，硕士研究生，主要从事海岸和近海工程研究。E-mail：lucktangweiluck@163.com