浮式结构物二阶波浪力求解方法比较研究

欧绍武，付世晓

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240; 2. 高新船舶与深海开发装备协同创新中心，上海 200240)

浮式结构物二阶波浪力求解方法比较研究

欧绍武1, 2，付世晓1, 2

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240; 2. 高新船舶与深海开发装备协同创新中心，上海 200240)

对远场法、近场法和中场法这几种常用的二阶波浪力计算方法进行了总结，并结合算例对它们之间的差异进行了研究，重点分析了网格密度、浮体形状、水深等因素的影响。此外，还对全QTF法和Newman近似这两种不规则波中的二阶力计算方法进行了讨论，比较了不同水深条件下两种方法求得的二阶波浪力谱之间的差异。研究结果表明，远场和中场法给出的结果基本一致，且具有较好的数值稳定性；而近场法受网格密度、浮体形状等因素影响较大；Newman近似给出的结果在频率较低时与全QTF法接近，但在频率较高时存在一定的误差。

二阶波浪力；远场法；近场法；中场法；全QTF法；Newman近似

Abstract: The commonly used methods in calculating second-order wave drift forces, such as far-field integration, near-field integration and middle-field integration, are summarized. The difference between these methods are studied by several examples, with special emphasis on element density, model shape and water depth. In addition, the drift forces in irregular sea with different water depths are calculated by both full-QTF method and Newman’s approximate, and the difference between two methods is further discussed through spectrum analysis. The results show that far-field integration and middle-filed integration give similar results with better robustness, while near-field integration is largely influenced by element density and model shape. It also shows that the results given by the Newman’s approximation are close to those by the full QTF method at low frequencies, but with certain errors when the frequency is higher.

Keywords: second-order drift force; far-field integration; near-field integration; middle-field integration; full-QTF; Newman’s approximate

对于海洋结构物而言，在不规则波浪的作用下，受到的波浪力包含一阶和二阶成分。一阶波浪力幅值较大，与波高成线性关系且频率与波浪相同。而二阶波浪力包括定常二阶力、低频二阶力和高频二阶力三部分，幅值相对较小，且与波高的平方成比例。由于二阶波浪力的存在，使得波浪中的海洋结构物不仅存在波频的摇荡运动，而且还存在长周期的漂移运动，这一运动的频率远低于不规则波的特征频率。对于锚泊的海洋浮式结构物如FPSO、半潜平台等而言，二阶波浪力中的低频成分有可能与锚泊系统的固有频率接近而产生共振，从而引起相当大的水平运动，在锚泊系统中产生较大的附加应力，对锚泊系统的安全构成威胁。

对二阶波浪力的深入研究源于20世纪60年代。Maruo[1]在由自由面、物面以及一个远离浮体的控制面围城的流域内，应用动量和能量守恒方程，得到了浮体在规则波中的平均二阶力的表达式。该理论之后由Newman[2]及Faltinsen等[3]加以推广。上述方法均是在远离浮体的控制面上积分，具有计算简便的优点，但只能求出二阶力中的定常部分，被称为远场积分法。后来，Molin[4], Pinkster[5], Ogilvie[6]等提出了压力积分法，直接求出物面上压力的所有二阶分量，然后在物面上积分，求得二阶力在各坐标轴上的分量。这种方法又被称为近场积分法，它可以清晰地显示出二阶力的各种组成部分，能够用于计算定常、低频和高频二阶力。但与远场积分相比，该方法计算相对复杂费时，计算结果容易受物面形状及网格划分的影响。近年来，Chen[7]在近场积分法的基础上提出一种新的二阶力计算方法，被称为中场积分法。其做法是首先在浮体附近建立一个控制面，然后利用斯托克斯公式和高斯公式，将近场积分法公式中对物面的积分转化成在控制面及平均水线面上的积分。这一方法能够用于计算定常、低频和高频二阶力，同时，由于控制面可以选取解析的性状，避免了浮体表面网格划分对速度势求解精度的影响，具有较好的数值稳定性。

对不规则波中的浮式锚泊系统而言，低频二阶力预报是十分重要的。对于低频二阶力的计算，可以采用近场积分法或者中场积分法求解完整的二阶传递函数矩阵，被称为全QTF法，但这些方法需要求解二阶速度势，求解过程极其耗时。工程中常使用Newman[8]提出的利用定常二阶力近似低频二阶力的方法，该方法被称为Newman近似。

在锚泊浮式海洋结构物的运动响应预报中，选取合适的方法，对二阶波浪力进行准确考虑是十分重要的。在以往的研究中，有学者曾分别对上述方法中的某一种或两种的特点进行过讨论[9-12]，但这些研究均是基于某一特定的船型开展的，得出的结论存在一定的局限性。本文首先对上述几种常用的二阶力计算理论进行了梳理，随后结合一些算例就网格划分、物体形状、水深等因素对这几种方法计算结果的影响进行了分析，并在此基础上对它们的适用性进行了讨论。

1 基本理论

1.1势流理论

为了讨论浮体在波浪中的运动，这里定义三个坐标系[13]，分别是：大地坐标系OXYZ，原点位于静水面上，用于描述波浪入射角β；随体坐标系OAXAYAZA，原点固结在浮体重心处，随船一起摇荡；参考坐标系OBXBYBZB，原点始终位于浮体的平衡位置，不随浮体一起摇荡，当浮体静止时，其与随体坐标系重合。三个坐标系均为右手系，Z轴垂直向上，浮体静止时，三个坐标系的X,Y轴平行，如图1所示。

图1 坐标系及浪向角定义Fig. 1 Definition of coordinate system and wave direction

本文讨论的浮体二阶波浪力计算基于势流理论，流体满足无黏、无旋、不可压缩三个基本假定，当简谐的入射波频率为ω时，总的速度势可以表示为：

其中，φI是入射势；φD为绕射势，是固定不动的结构物在入射波作用下产生的速度势；φR表示辐射势，是浮体在静水中摇荡产生的速度势。φp=φD+φR是由于结构物存在而产生的速度势，又称为扰动势。

速度势满足下列定解条件：

1)Laplace方程：

2φ=0 (流域内)

2)统一的线性化的自由面条件：

3)物面条件：

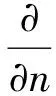
其中，(n1,n2,n3)=n，(n4,n5,n6)=r×n，n表示浮体表面某点的单位外法向量；r表示从浮体随体系原点到该点的矢径。

4)水底条件：

5)远方辐射条件：

假设海底是水平的，自由表面无限长，根据Airy波理论可以得到入射势的表达式为：

其中，A为波幅，β为浪向角，h为水深，k为波数。由色散关系确定：

辐射势和绕射势的定解问题可以利用格林函数法求得。在柱坐标系(R,θ,z)下，距离浮体很远(R→∞)的某点的绕射势和辐射势可以表示为[7]：

其中，K(θ)称为Kochin函数，定义为：

式中：S为浮体的湿表面；σ(Q)为表面的源强。

1.2远场法

远场法的基本思想是在由物面S、自由面SF、半径无限大的垂直柱面S∞和水底平面SB围成的流域内，运用动量和能量守恒方程，得到浮体所受的平均二阶力。Newman[2]给出的平均二阶力的表达式为：

从表达式来看，远场法是在一个柱面上积分，对浮体表面网格划分不敏感，因此具有较好的数值稳定性，在工程中被广泛应用。但同时，由于远场法需要选取无限大控制面，故只能用于计算单浮体的平均二阶力。

1.3近场法

近场法的基本思想是直接求出物面上压力所有的二阶分量，并在物面上进行积分，以求得二阶波浪力(力矩)在各坐标轴上的分量。具体做法是将速度势、压力、瞬时波面升高、运动向量等均展开成ε的级数的形式，然后在浮体的瞬时湿表面上积分，并精确至二阶[13]：

注意式中已将浮体的瞬时湿表面分成平均湿表面S0，和因波浪及浮体运动引起的湿表面变化ΔS。式中带括号的上标(0)、(1)、(2)表示对应物理量的阶次。

p(0)，p(1)，p(2)分别为静压力、一阶动压力和二阶动压力，由下面的式子确定：

注意这里为了避免混乱，引入了符号x1,x2,x3来表示x,y,z三个方向。类似的，后面还将使用α1,α2,α3来表示α,β,γ三个欧拉角。式中，向量X表示浮体表面一点在参考坐标系下的位置，定义为：

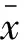
浮体表面法向N的定义与X类似，为：

N=n+α(1)×n+D·n=n(0)+εN(1)+ε2N(2)

将上面式子代入式(18)，保留二阶项可以得到二阶漂移力的表达式如下：

在不规则海况中，入射波可以记为各种频率的规则波的叠加，即：

若只研究差频二阶力，则可将表达式化简成以下形式：

从近场法的推导过程可知，该方法具有普适性，能应用于单体或者多体系统，并能够给出六个自由度上包括定常、低频和高频成分在内的所有二阶力分量。但由于近场法需要在船体表面积分，在船体表面存在尖角的地方容易产生奇点，进而对计算结果造成影响。

1.4中场法

中场法从近场法发展而来，其基本思想是在浮体附近建立一个封闭的控制面，然后对近场法的二阶漂移力计算公式使用双参数的斯托克斯公式和高斯公式，将其转换成在浮体表面S、自由面SF及控制面C上的积分[7]，即：

F=ρ∬S[Φ(·n)+()(X·n)]ds-ρg∮ΓΘkdl-

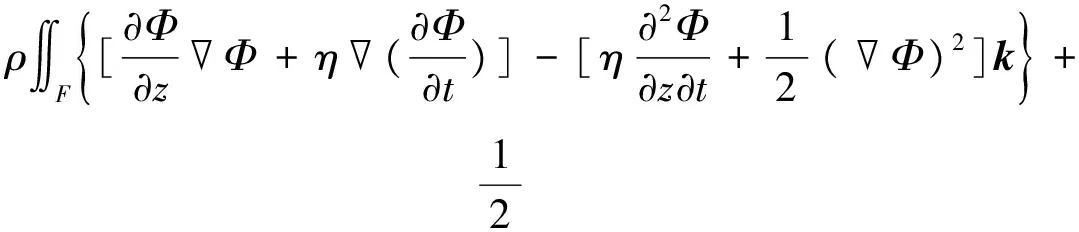
M=ρ∬Sx×[Φ(·n)+()(X·n)]ds-ρg∮ΓΘ(x×k)dl-

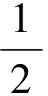
式中：Γ为浮体与自由面的交线；ΓC为控制面与自由面的交线；Θ定义为：

式(22)，(23)是通用的公式，可用于计算包括和频和差频成分在内的六个方向上的所有二阶力。若只需计算平面内三个方向(横荡、纵荡和艏摇)的平均二阶力，则可将上述公式进一步简化成在控制面及其与自由面的交线上的积分，即：

式中：〈·〉表示在一个周期内取平均值。

从表达式来看，中场法将积分转换成了在控制面及其与自由面交线上的积分，受物体几何形状影响较小，能够应用于单体或者多体的情况，并能给出六个自由度上的定常、低频及高频二阶力。

1.5Newman近似

对不规则波中的浮式锚泊系统而言，低频二阶力预报是十分重要的。对于低频二阶力的计算，常用的方法主要有两种：第一种是利用近场法式(19)或者中场法式(22)、式(23)直接计算完整的QTF矩阵，然后根据不规则波时历计算低频二阶力，被称为全QTF法；另一种方法是根据规则波下计算得到的平均二阶力，使用近似的方法得到QTF矩阵，其中使用最广泛的是Newman近似。

一般而言，ωi,ωj平面内的所有频率均对二阶力有贡献，但二阶力的幅值通常都比较小，因此只有频率接近锚泊系统固有频率的二阶力会对浮体的运动响应有明显影响。频率差Δω等于固有频率ωn在ωi,ωj平面内表示两条线ωi=ωj±ωn，而大多数情况下，浮式锚泊系统在水平面内运动的固有频率都远小于波浪频率，此时这两条线接近QTF矩阵的对角线。Newman近似[8]认为，这种情况下QTF矩阵中的非对角元素Tωi,ωj可以用对角元Tωi,ωi来表示：

上式是原始的Newman近似公式，该式还有多种修正的表达式，其中使用最多的是[14]：

与全QTF法相比，Newman近似能够极大地提高计算效率，在浮式锚泊系统固有频率很低的情况下有较高的精度，但其完全忽略了二阶速度势的影响，在某些情况下的正确性有待讨论。

2 数值计算

2.1数值模型

本文的数值计算主要基于Hydrostar软件[15]，共涉及到两种主尺度相近的模型，分别是方Weigly船和半椭球体，其主要参数如表1所示。

表1 模型的主要参数Tab. 1 Models’ main characteristic parameters

2.2浮体形状及网格划分的影响

为了研究网格划分对不同二阶力计算方法的影响，选取网格数为400、800、1 200、2 000和4 000五种情况，进行比较分析。数值计算中的波浪频率选取为0.05～2.5 rad/s，间隔0.05 rad/s，浪向角选取45°，浮体湿表面及中场积分法所用的控制面如图2所示。

图2 湿表面及控制面模型(网格数N=1 200)Fig. 2 Panel model of control surface and wet surface (element number N=1 200)

图3给出了不同网格密度下Weigly船的一阶纵荡、横荡和艏摇运动RAO。其中，无符号的曲线表示纵荡；带“o”的曲线表示横荡；带“*”的曲线表示中场法艏摇。从计算结果来看，各网格密度下的结果吻合得很好，表明网格密度对一阶运动RAO没有明显的影响。

图3 不同网格密度下Weigly船和椭球体的运动RAOFig. 3 Motion RAOs of weigly ship and ellipsoid with different element densities

图4给出了不同网格密度下，分别用远场法、近场法和中场法计算平均二阶力的结果。其中，带“x”的曲线表示远场法；带“o”的曲线表示中场法；无符号的曲线表示近场法。

图4 不同网格密度下Weigly船和椭球体的平均二阶力Fig. 4 Mean drift force of Weigly ship and ellipsoid with different element densities

总体而言，三种方法给出结果随频率的变化趋势相同，中场法和远场法给出的结果基本一致，且具有较好的收敛性。对于算例中的两个模型，当网格数大于1 200时，中场法和远场法的结果基本不再随网格数变化而变化；但对于近场法，在波浪频率较大时，不同的网格密度下计算结果有较大的差异，随着网格密度的提高，近场法与其它两种方法的结果有趋同的倾向。此外，在波浪频率较低时，三种方法的结果基本一致，但随着波浪频率的增大，近场法的结果与远场法和中场法的结果出现了一定的差异。值得注意的是，在波浪频率为0.75～1 rad/s时，近场法给出的Weigly船的纵荡二阶力与中场法和远场法的结果有较大的差异，其原因可能是Weigly船的表面存在尖角，进行压力积分时这些地方容易产生奇点，进而对计算结果造成影响。相比之下，表面相对光滑的椭球体则不存在这类问题，波浪频率较低时(1.2 rad/s以下)三种方法的结果基本一致。

2.3水深的影响

一般而言，不同水深下浮体所受的波浪力及其运动响应存在一定的差异，常用的三种二阶波浪力计算方法的原理不同，其在不同水深条件下给出的预报结果可能存在一定的差异。为了比较这种差异，这里以椭球体为例，网格数选取N=2 000，水深与吃水之比选取无限大(inf)，10，5，2，1.5五种情况进行分析，如图5所示。其中，带“*”的曲线表示远场法；带“o”的曲线表示中场法；无符号的曲线表示近场法。从图5中的结果来看，在各种水深条件下，远场法给出的结果均与中场法一致。而对于近场法，由于算法的不同，在算例中的几种水深条件下，给出的平均二阶力结果与远场法和中场法略有差异，但随水深变化的规律与基本一致，即随水深的变浅而有一定程度的增大。这一现象表明，在浅水条件下预报平均二阶力时，三种方法均适用。

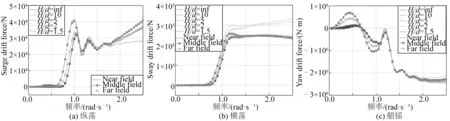
图5 不同水深下椭球体的平均二阶力Fig. 5 Mean drift force of ellipsoid at different water depths

2.4Newman近似与全QTF法的差异

由于Newman近似简单地根据二阶传递函数的定常项(对角元项)得到QTF矩阵的其余部分，这种做法难免会带来一定的误差。

图6 椭球体的横荡QTF矩阵Fig. 6 Sway QTF matrix of ellipsoid

为了研究Newman近似与全QTF法的差异，这里以椭球体为例，网格数选取N=2 000，水深/吃水选取无限大，利用中场法求得平均二阶力，然后利用Newman近似求出近似的QTF矩阵，如图6(a)所示；图6(b)则给出了直接用中场法求出的完整的QTF矩阵。由图可知，在对角线附近(图中两根虚线之间的位置)，两种方法给出的结果基本一致，表明两种方法对二阶力中频率很低的部分预报结果是相近的。但在远离对角线的位置，两者存在明显的差异，Newman近似得出的QTF矩阵较为平滑，具有明显的规律性；而全QTF法的结果在非对角元上波动较大，存在明显的峰谷交替现象。这一结果表明，两种方法对频率稍高的二阶力成分预报的结果可能存在差异。

为了进一步说明两种方法的预报结果的差异，根据式(21)计算了不同水深条件下，不规则波中椭球体所受的二阶力时历，并进一步利用FFT给出了相应的二阶力谱，如图7所示。其中不规则波选取ITTC双参数谱，有效波高Hs=1 m，特征周期T1=4.6 s，其谱形如图8所示。

图7中H/d表示水深与吃水之比，其中虚线表示Newman近似的结果，带“o”的实线表示全QTF法的结果。显然，在频率较低的情况下(小于0.1 rad/s)，Newman近似与全QTF法给出的结果基本一致；但在稍高的频段内(0.1～0.8 rad/s)，两种方法存在明显的差异，大多数情况下，Newman近似的结果明显大于全QTF法的结果。此外，在水深较小的情况下(H/d=1.5)，全QTF法的结果中，0.2～0.6 rad/s范围内的艏摇二阶力明显大于Newman近似的值，原因是浅水条件下二阶速度势对二阶力有较大的贡献，而Newman近似完全忽略了这一项的影响，从而导致较大的误差。

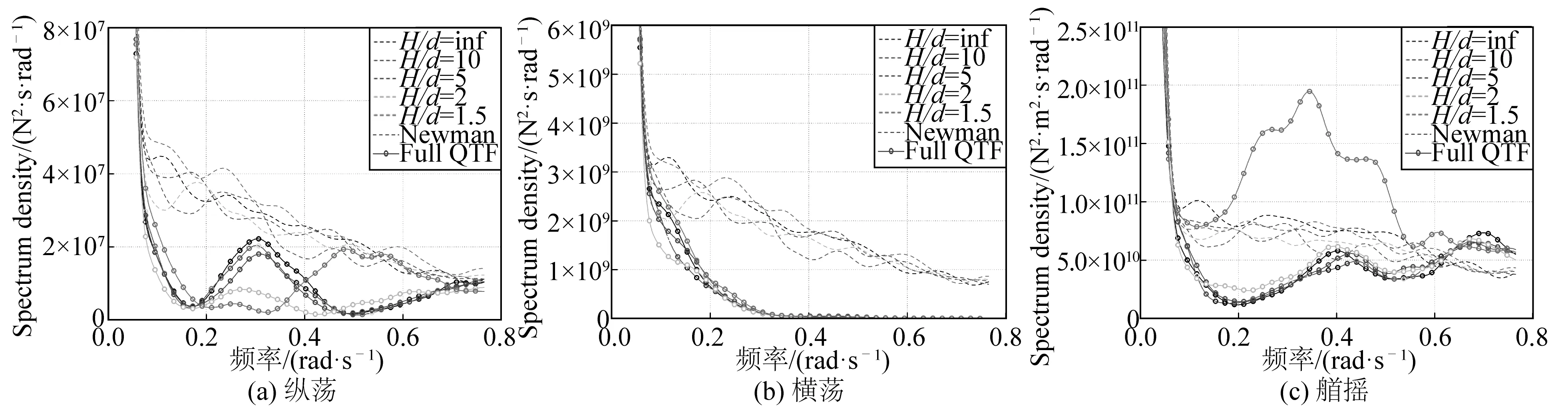
图7 椭球体的横荡二阶力谱Fig. 7 Sway drift spectrum of ellipsoid

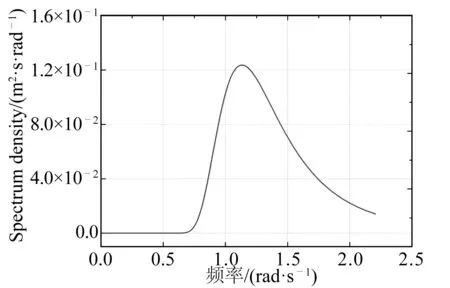
图8 ITTC双参数谱(Hs=1 m， T1=4.6 s)Fig. 8 Two-parameter ITTC spectrum (Hs=1 m， T1=4.6 s)

3 结 语

通过上述讨论，可以得出以下结论：

1) 远场积分法只能用于单浮体计算，能给出纵荡、横荡和艏摇三个自由度上的平均二阶力；近场积分法清楚地解释了二阶力的来源，具有普适性，能应用于单体或者多体系统，并能够给出六个自由度上包括定常、低频和高频成分在内的所有二阶力分量；中场积分法能应用于单体或者多体系统，也能用于计算二阶力的定常、低频和高频部分。

2) 三种方法给出的结果在波浪频率较低时(1.2 rad/s以下)差异不大。但随着波浪频率的提高，远场法与中场法表现出更好的数值稳定性，网格密度对结果影响不大；相比之下，近场法的结果受网格密度影响比较明显。此外，使用近场法计算具有尖角的结构时可能会出现误差。

3) 三种方法给出的平均二阶力随水深变化的规律一致，即随水深的变浅而有一定程度的增大，表明这三种方法对深水或浅水的情况均适用。

4) Newman近似与全QTF法给出的结果在对角线附近基本一致，但在远离对角线的位置，两者存在明显的差异。从不规则波下的响应谱来看，在频率很低(0.1 rad/s以下)的情况下，Newman近似与全QTF法给出的结果基本一致；但随着频率的增大，Newman近似出现了明显的误差。此外，在水深较浅的情况下，二阶速度势对二阶力有较大贡献，导致浮体某些自由度的低频二阶力将会发生明显的变化，但Newman近似忽略了这一影响。

[1] MAURO H. The drift of a body floating on waves[J]. Journal of Ship Research, 1960, 4: 1-5.

[2] NEWMAN J N. The drift force and moment on ships in waves[J]. Journal of Ship Research, 1967, 11(1): 51-60.

[3] FALTINSEN O M, MICHELSEN F C. Motions of large structures in waves at zero froude number[J]. International Symposium on the Dynamics of Marine Vehicles and Structures in Waves, 1975, 90:3-18.

[4] MOLIN B. Computations of wave drift forces[C]//Proceedings of the offshore Technology Conference. 1979: OTC-3627-MS.

[5] PINKSTER J A. Low frequency second order wave exciting forces on floating structures[D]. TU Delft, Delft University of Technology, 1980.

[6] OGILVIE T F. Second-order hydrodynamic effects on ocean platforms[M]//International Workshop on Ship and Platform Motions. Berkeley: University of California, 1983.

[7] CHEN X B. Middle-field formulation for the computation of wave-drift loads[J]. Journal of Engineering Mathematics, 2007, 59(1): 61-82.

[8] NEWNAN J N. Second-order, slowly-varying forces on vessels in irregular waves[J]. Marine Vehicles, 1974: 182-186.

[9] KASHIWAGI M, ENDO K, YAMAGUCHI H. Wave drift forces and moments on two ships arranged side by side in waves[J]. Ocean Engineering, 2005, 32(s 5-6):529-555.

[10] INOUE Y, ISLAM M R. Numerical investigation of slowly varying drift forces of multiple floating bodies in short crested irregular waves[C]//Proceedings of the Tenth International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2000.

[11] MALENICA &, OROZCO J M, CHEN X B. Some aspects of multibody interactions in seakeeping[C]//Proceedings of the Fifteenth International offshore and Polar Engineering Conterence. International Society of Offshore and Polar Engineers, 2005: ISOPE-1-05-250.

[12] NACIRI M, BUCHNER B, BUNNIK T, et al. Low frequency motions of LNG carriers moored in shallow water[C]//Proceedings of the 23rd International Conference on Offshore Mechanics and Arctic Engineering. 2004:995-1006.

[13] 刘应中，缪国平. 船舶在波浪上的运动理论[M]. 上海: 上海交通大学出版社, 1987. (LIU Y Z, MIAO G P. Motion theory of ship on waves[M]. Shanghai: Shanghai Jiao Tong University Press, 1987. (in Chinese))

[14] DNV-RP-C205, Environmental conditions and environmental loads[S]. Veritas D N, 2010.

[15] Veritas B. Hydrostar for experts user manual[S]. 2010.

A comparative study on the numerical methods of second-order drift forces on floating structures

OU Shaowu1, 2, FU Shixiao1, 2

(1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China)

U661.1

A

10.16483/j.issn.1005-9865.2017.04.013

1005-9865(2017)04-0100-10

2016-08-15

欧绍武(1991-)，男，硕士研究生，主要从事多体水动力研究。E-mail:shaowuloveh@163.com

付世晓。E-mail:shixiao.fu@sjtu.edu.cn