我国滨海核电站防护工程设计标准研究
2017-10-12刘德辅史宏达刘桂林王风清
刘德辅,史宏达,刘桂林,王风清
(中国海洋大学,山东 青岛 266003)
我国滨海核电站防护工程设计标准研究
刘德辅,史宏达,刘桂林,王风清
(中国海洋大学,山东 青岛 266003)
面对全球极端气候频发的趋势,国内外核电站海岸防护工程普遍采用“可能最大台风暴潮”、“设计基准洪水”等具有含混性的规定作为确定防灾设计标准的依据,其内涵的各种不确定性因素必然会对防灾决策带来重大的致灾隐患。按照国务院核电站安全规划(2011-2020)提出的“必须按照全球最高安全要求”,全面开展滨海核电站防护工程设计标准研究己势在必行。使用多维复合极值分布理论及双层嵌套多目标联合概率模式,将核电站水文与气象的研究标准合二为一,对IAEA及我国滨海核电站防护工程设计标准进行了风险评估,供有关部门参考。
滨海核电站;防护工程;设计标准;设计基准洪水;多维复合极值分布;风险评估
Abstract: With the tendency of increasing extreme natural hazards, the typhoon, hurricane, and tropical cyclone induced surges, waves and rainstorms menace Nuclear Power Plants (NPP) in coastal areas. National Nuclear Safety Administration of China and International Atomic Energy Agency (IAEA) have recommended safety regulations for NPP site evaluation installation and coastal defence infrastructures. These standards include Probable Maximum Hurricane /Typhoon (PMH/T), Probable Maximum Storm Surge (PMSS), Probable Maximum Flood (PMF) as well as Design Basis Flood (DBF). According to the 2011-2020 safety planning of China State Council for nuclear power plants, it is necessary to do a comprehensive research on design standards for protective engineering and structural technology of the NPP based on the world’s highest safety requirements. This paper discusses the joint probability analysis of meteorological and oceanographic factors based on our proposed Compound Extreme Value Distribution (CEVD), Multivariate Compound Extreme Value Distribution (MCEVD), and Double Layer Nested Multi-Objective Probability Model (DLNMOPM), and ours are compared with IAEA recommended safety regulation design criteria for NPP coastal defence infrastructures in China.
Keywords: nuclear power plants; protection engineering; design standard; design basic floods; multivariate compound extreme value distribution; risk assessment
随着全球气候变暖和海平面上升等因素加剧的趋势,台风、巨浪、风暴潮、暴雨和洪灾等已成为影响滨海核电站防护工程安全的重大问题。日本核电灾害发生后,许多学者对地震-海啸的研究表明:当Manila和Rykyu海沟发生9级地震时,对我国东南沿海诱发的海啸巨浪不超过6 m[1]。世界气象组织指出:百分之九十的自然灾害为极端气象灾害,例如台风、飓风和热带风暴灾害。台风是威胁我国滨海核电站的最重要致灾因素。研究台风、巨浪、风暴增水、暴雨、洪水及其与天文大潮组合的小概率极端事件发生的可能性非常必要。2006年桑美台风诱发的7 m巨浪和3.8 m风暴增水造成沙埕港千艘船只毁坏和多人死亡。如果台风延后两小时登陆,则恰逢天文大潮,这种“三碰头”的组合,可完全淹没包括核电站在内的福建和浙江大部分土地,其灾难性后果难以估量。虽然这属于小概率极端事件,但是这类事件的发生是完全可能的。因此,按照国务院核电站安全规划(2011-2020)提出的“必须按照全球最高安全要求”,全面开展滨海核电站防护工程设计标准研究己势在必行。必须重新检验核电站防护工程设计标准应对各种极端自然灾害的可靠性。目前我国滨海核电站设计基准洪水位的计算分析以确定论方法为主,以“10%超过概率天文高潮位+可能最大风暴潮增水及百年一遇波高”的组合作为防护工程设计标准。但是,在计算防护工程标准时,我国核电站有关规范的“可能最大风暴潮增水”、“设计基准洪水”(DBF)、IAEA2006-2009和U.S.NRC 2011在新的安全规程中提出的“风暴潮、天文潮和巨浪的组合”[2-8]内涵各种不确定性因素,这些不确定性因素必然会对防灾措施的决策带来重大的致灾隐患。因此,在港口、海岸、近海及河口城市防护工程的设计中,由于概率统计理论和方法上的限制,无法考虑恶劣环境条件下多种荷载共同作用的问题必须得到妥善解决。
1 复合极值分布理论(CEVD)及多维复合极值分布理论(MCEVD)的建立
国内外惯用年极值系列按照某种概率模式(如P-Ⅲ型、Gumbel,Weibull分布)外延推求不同重现期设计值。但这种作法存在的弊端——遗漏了每年各次台风致灾因素提供的重要信息,影响到概率预测结果的置信度。考虑到台风影响不同海区每年出现的频次各不相同,可用离散型随机变量及相应的离散型概率分布表示;而台风诱发的致灾因素(风速、增水、波高等),则可用连续型极值分布表示。二者的组合在顺序统计学和测度论的理论基础上,经过严格的数学推导,可构成一种新的极值分布模式——复合极值分布(compound extreme value distribution,简称CEVD)。根据统计检验结果,台风(飓风)影响各海区的频次符合Poisson分布,台风(飓风)波浪的不同特征,可分别采用Gumbel和Weibull分布,则可构成Poisson-Gumbel CEVD分布(用于我国台风影响海域)[9]和Poisson-Weibull CEVD分布(用于美国墨西哥湾和大西洋沿岸)[10]。
近年来,CEVD完成了从一维拓宽到多维复合极值分布(multivariate compound extreme value distribution,简称MCEVD)的理论推导和相应工程应用。2005年美国Katrina飓风对新奥尔良的毁灭性破坏,进一步验证了CEVD模式应用于飓风概率预测结果的正确性[11-17]。2006年有关文献[18-19]在重要国际会议和刊物公开发表后,得到了国际学术界的高度评价。2008年交通部在国家行业标准“海港水文规范”(JTJ213-98)修订稿中,正式采用了“复合极值分布理论”作为设计波高概率预测的理论和方法,首次取代了该国家行业标准中持续使用近四十年的P-Ⅲ型曲线。2008年美国佛罗里达国际飓风研究中心在海岸防护飓风灾害工程设计中,引用文献[9-10,19-20]作为防护飓风灾害设计标准的依据[21]。多年来MCEVD用于城市防灾、三峡防洪、防灾区划、奥帆工程、海洋平台和滨海核电站防护工程设计标准的风险分析以及暴雨,洪水诱发滑坡、泥石流等致灾因素概率预测研究成果[22-34];有关内容被美国NOVA科学出版社收录在《Natural Disasters: Prevention, Risk Factors and Mitigation》一书的第一章“Typhoon/Hurricane/Tropical Cyclone Disasters: Prediction, Prevention and Mitigation”中[35];2015年美国NOVA科学出版社再次将有关内容收录在学术专著《Risk Assessment for Nuclear Power Plants against Natural Disasters: Probability Prediction and Disaster Prevention Infrastructures》中[36]。
2 预测结果比较
2005年美国发生的Katrina飓风重灾,导致新奥尔良市毁灭性破坏,1 800人死亡,800亿美元经济损失。这次飓风的强度和特征,符合1982年使用复合极值分布理论模式预测结果[10](表1),显示2005灾后使用MCEVD复核结果的合理性[20,37];同时也表明美国国家海洋和大气管理局(NOAA)制订的上述海区防灾标准的可能最大飓风(PMH)和标准设计飓风(SPH)过低,相关文献[38-39]也得到相同的结果。
2012年10月30-31日桑迪飓风造成堤坝冲毁,特拉华州、新泽西州及纽约周边大面积淹没,大量人员伤亡,数百亿美元经济损失,再次表明传统的设计标准和工程结构标准过低,我们对上述海区飓风强度预测成果再次得到证实[10]。
使用2002年以来新开发的 MCEVD分析飓风及其诱发的极端风速的预测值明显高于2005年以前美国不同学者公开发表对上述海域预测成果(图1)。同时,MCEVD的预测结果还显示,重现期100年一遇的风速在3区(新奥尔良区)的预测值与2005卡特里娜飓风状况相近,明显高于设防标准;8-9区(新泽西,纽约沿岸)的预测值则与2012年桑迪飓风最大风速相近(表2)。

表1 墨西哥湾A区卡特里娜飓风强度概率分析Tab. 1 Probability analysis for hurricane Katrina in Gulf of Mexico area A

表2 不同方法预测结果比较Tab. 2 Predicted results by different models
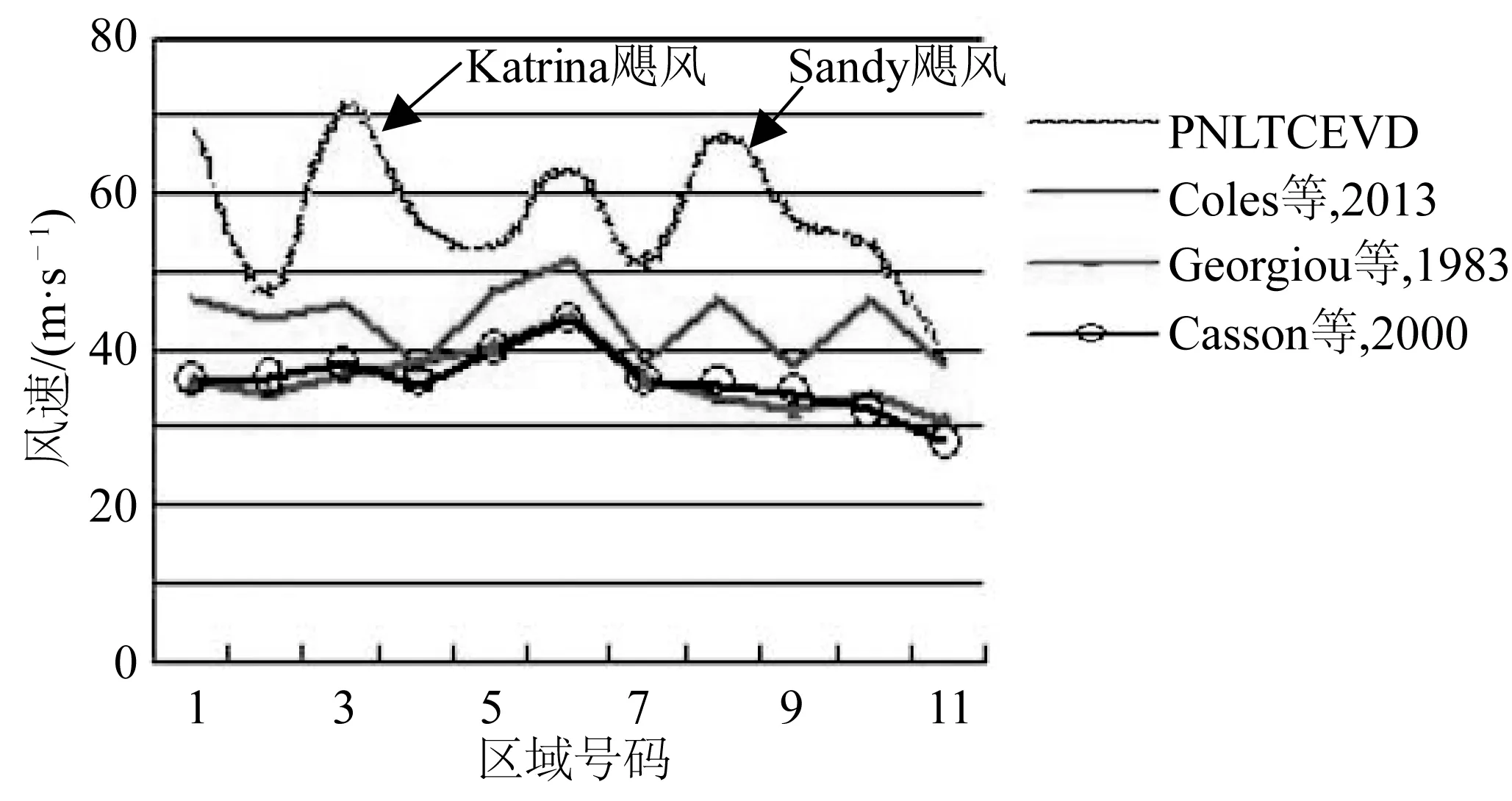
图1 100年一遇的极端风速概率预测Fig. 1 Predicted 100 a return value of extreme wind velocities

图2 美国大西洋沿岸各区不同重现期风暴潮增水预测结果Fig. 2 1982 predicted storm surges with different return periods in US Atlantic areas
如图2所示,1982年预测的费城周边(图中虚线)100年一遇风暴潮增水为3.048 m,与2012年10月30日8时06分桑迪飓风造成的费城周边3.237 m的实测水位相当,而美国国家海洋和大气管理局(NOAA)对该区的预测值仅为2.292 m。
2013年台风菲特带来重大经济损失,浙江、上海多处出现超警戒水位洪水,多处防护工程倒塌。以台风菲特对上海影响为例(如表3所示),考虑台风暴潮、暴雨洪水与天文大潮的组合,2006年使用MCEVD计算的100年一遇预测结果,已大大超过上海防护工程500年一遇超警戒水位设防标准。2013年10月8日,受天文大潮顶托、上游洪水下泄、本地大暴雨和台风暴潮的共同影响,黄浦江沿线水位迅速上涨,下午2时05分,吴淞口实测水位达5.15 m,超过警戒水位0.35 m,仅达到MCEVD计算的60年一遇预测值[36-37,40-42]。
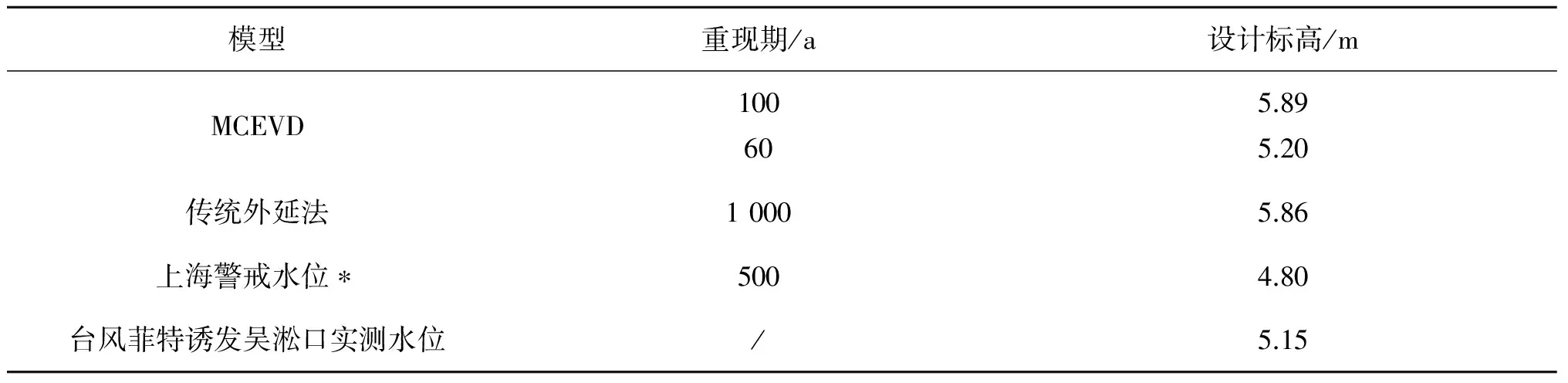
表3 考虑台风暴潮,暴雨洪水与天文大潮使用MCEVD和传统外延法预测结果比较Tab. 3 Comparison between MCEVD predicted combined storm surge, flood and spring tide with traditional method
注:*代表传统规范外延法预测结果。
3 使用CEVD进行滨海核电站防洪裕度分析
为了弥补用年极值系列按照某种概率模式外延推求不同重现期设计值作法存在的遗漏每年各次台风波浪提供的重要信息的弊端,CEVD模式将台风每年影响不同海区的频次作为一组离散型随机变量引入模型,增加了可利用的资料信息;同时研究P-III、Gumbel及其与CEVD 对超低概率极值的拟合能力以及置信度水平的对比,以保证滨海核电站防洪安全裕度评估的正确性。

图3 三种分布的拟合平均差v对比图Fig. 3 Comparison between three models calculated v
为验证CEVD理论预测结果的正确性和可靠性,我们使用滨海核电站周边长期实测资料,对Gumbel,P-Ⅲ和CEVD分布的拟合最大偏差Dn,平均差v,标准差d,不同重现期概率预测值置信区间ΔH进行了比较。将中国科学院南海海洋研究所提供的大鹏湾1951-2002实测(缺测部分为后报)近岸风、浪资料,分别按各20年为一组进行滑动取样,对Gumbel,P-Ⅲ和CEVD分布的拟合优度,按拟合最大偏差Dn,拟合平均差v和拟合标准差d进行比较,比较结果如图3及表4所示。有关统计特征及拟合优度说明,详见文献[35,43]。

表4 三种分布拟合优度参数及其变化范围Tab. 4 Relative differences of predicted returns value between three models
由表4和图3所示,无论是拟合最大偏差Dn,还是拟合平均差v和拟合标准差d,CEVD的拟合偏差数均小于P-III分布和Gumbel分布。

表5 大鹏湾不同重现期概率预测值及置信区间ΔH对比计算结果Tab. 5 Comparison between predicted return values with confidence intervals by three models
表5所示P-III、Gumbel以及其与CEVD对超低概率极值的拟合能力以及置信度水平的对比表明:CEVD是迄今为止可保证滨海核电站防洪安全裕度评估正确性的模式。
4 滨海核电站防护工程设计标准地构建
目前国际上多要素联合概率理论研究(如Copula理论等)都建立在年极值取样或过阈取样(POT)的基础上,但年极值取样遗漏了每年台风诱发的暴潮、波浪等要素的大量信息;POT取样联合概率则无理论依据[25,44-45]。多维复合极值分布理论(MCEVD)将极值过程取样与联合概率结合起来,增加了资料信息,缩小了概率预测的误差范围。既可满足特大值的概率预测,又可进行多种致灾因素联合出现的概率预测。美国学者在《美国洪水概率分析总结》中引用了复合极值分布理论并指出“把事件取样(过程取样)和联合概率结合起来,将大大推动特大洪水概率预测的发展”[11]。MCEVD正是迄今为止能满足这种期待的唯一理论模式,现已在多种工程应用中得到证实。MCEVD模式简介如下:
每年的台风频次λ符合泊松分布:
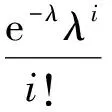
MCEVD可表示为:
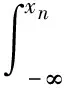
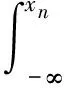
相应的概率密度函数为:

为解决MCEVD的理论解法,引入三元嵌套Logistic模型[46],其一般表达式为
由此可得应用于实际计算的“泊松嵌套逻辑三维复合极值分布”(poisson nested logistic tri-variant compound extreme value distribution,简称PNLTCEVD):
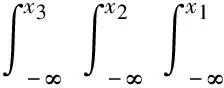
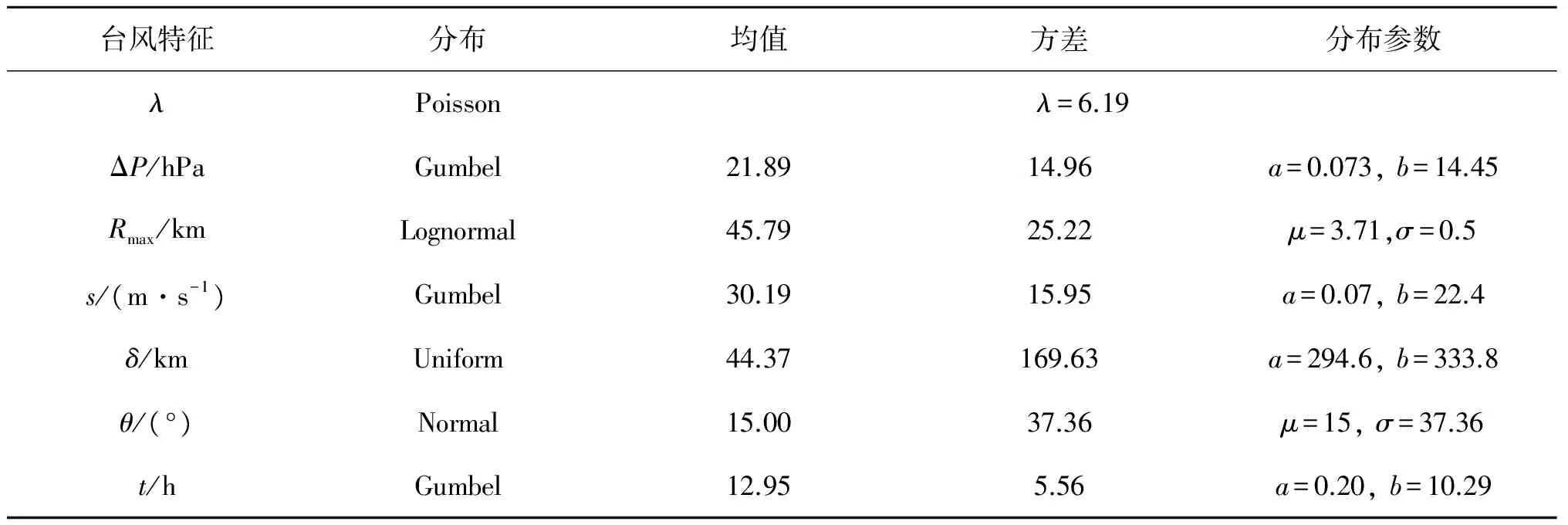
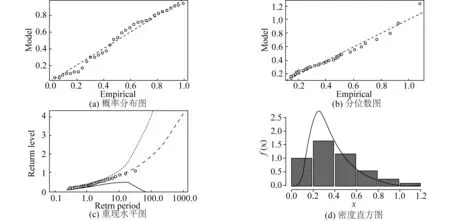
其中,ξj,μj,σj分别为xj(j=1,2,3)的边缘分布的形状参数、位置参数和尺度参数。通过矩估计法,得到相关参数α,β的显式表达式:
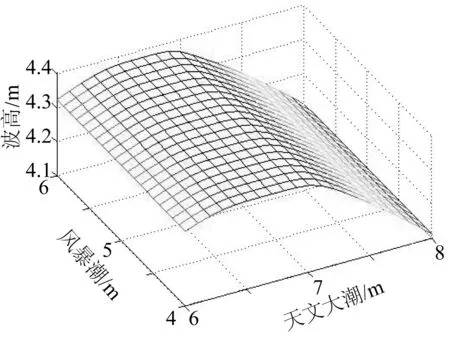
式中:ri,j为一般的线性相关系数,i PNLTCEVD成为显式形式,通过对边缘分布参数和相关参数的分别估计,可确定该模型的具体表达式。它结构简单,应用方便,考虑了三种环境荷载下的最不利遭遇组合,同时涉及两个相关参数,含概了变量之间相关的不对称性。三个变量的分层结构(α为外层,β为内层)表明x1,x2之间比x1,x3和x2,x3之间有着更强的相关性。 上述理论解法及相应的随机模拟计算软件,在国内外尚无先例。只需输入台风特征、各种致灾因素,进行边缘分布分析,统计检验,即可使用相应软件进行台风灾害概率预测[20,37]。 4.1台风特征的长期联合概率预测 由于每年台风频次、路径各不相同,在其形成、发展、登陆和消亡过程中,台风各种特征也不断变化,以致在我国沿海和内陆不同区域的台风特征组合也差异甚大。这些特征与致灾强度和后果都有直接关系。因此,研究不同区域台风特征组合及其相应后果分析,是台风灾害区划的重要组成部分。台风特征大多采用中心气压差(ΔP)、最大风速半径(Rmax)、台风移动速度(s)、台风中心与影响区域最小距离(δ)和台风移动方向角(θ)五种变量表示。复合极值分布理论的特点,在于将台风影响各区域的频次(λ)作为一种离散型随机量考虑。鉴于1975年尼娜台风在福建登陆,经历108个小时北上至河南省,导致暴雨—洪水巨灾,造成大量人员伤亡的悲剧,以及2006年碧利斯台风登陆后持续在内陆各省造成的伤亡,本模式将台风登陆至消亡的历时(t)也作为一种台风特征进行研究。对一种离散型分布(λ)和六种连续型分布的多维联合概率研究,用多维复合极值分布理论的随机模拟求解法,是可行的[35]。 4.2台风诱发不同致灾因素组合的联合概率预测 核电站防护设施风险评估程序如图4所示。图4中(b)、(c)分别为以随机-数值模型计算建立的资料系列及观测资料系列,对不同台风特征组合以及不同的核电站地理位置,分别对不同致灾控制因素(第一位)进行联合概率预测[20]。在台风诱发风暴潮、巨浪及相应天文大潮以及暴雨、大风等致灾因素的联合概率预测中,引入整体不确定性,整体敏感性分析(GUA,GUA)[47],在输入-输出过程中,反复调整输入值,计算其对输出的敏感程度,选择最不利的组合,进行联合概率预测,作为设防标准(图5)。 图4 核电站防护设施风险评估Fig. 4 Safety analysis of disaster prevention infrastructures for nuclear power plants 4.3海岸带防护工程结构的可靠度分析 按可接受风险分析原则(ALARP)进行防护工程结构可靠度分析(图4(d))。 按照国际上广泛采用的ALARP准则(as low as reasonable practice)[48],结构失效概率高于10-3为不可接受风险,低于10-7为可接受风险。使用多维复合极值分布理论的随机模拟求解法;针对防护工程结构特征,对防护工程结构抗力因素及风、浪、潮、流等外荷,使用多维复合极值分布理论的随机模拟求解法,对海洋平台,核电站进行防护工程结构失效概率分析[30-32]。同样也可用于越浪程度的分析,以保证其它工程结构的安全[27-29]。 图5 引入整体不确定性,整体敏感性分析(GUA,GUA)的联合概率分析Fig. 5 Joint probability prediction with Global Uncertainty Analysis (GUA) and Global Sensitivity Analysis (GSA) 岭澳核电站位于南海滨。海岸带台风诱发风暴潮、巨浪与伴生的天文大潮“三碰头”为主要致灾因素,在模型计算中对输入—输出体系引入整体不确定性(GUA)、整体敏感性(GSA)反复分析表明,台风诱发巨浪为致灾控制因素。按图4所示程序计算如下。 5.1输入因素不确定性分析 1) 天文大潮不确定性分析。通过调和分析和统计分析表明,每年的调和常数和平均水位都是不同,25年的调和常数和年平均水位进行不确定性和敏感性分析表明,调和常数和年平均海平面的变化每年不同,分别计算其平均值μ,均方差σ及变异系数COV[49]。 调和常数不确定性: μ=166.65;σ=0.88;COV1=σ/μ=0.005 3 平均海平面不确定性: μ=4.80;σ=3.96;COV2=σ/μ=0.825 6 天文大潮不确定性: COV=(COV12+COV22)1/2=0.825 2)极值波高概率预测不确定性分析[44] 概率预测模式不确定性:COV1=0.08 取样不确定性:COV2=0.09 统计不确定性:COV3=0.10 极值波高概率预测总体不确定性:COV=(COV12+COV22+COV32)1/2=0.156 3)置信区间估计公式[50] Hp=b+eβ=φ(β) 而 故 ΔHp即为相应某种重现值Hp的置信区间半长公式,置信区间(置信概率68.27%)为: HT+ΔHT,HT-ΔHT 5.2南海海区台风概率特征分析 南海海区台风各参数符合的概率分布和概率特征参数、分布参数如表6所示。 表6 南海海岸带台风概率特征Tab. 6 Marginal distribution of typhoon characters for South China Sea 5.3台风特征统计检验 台风特征统计检验图如图6(a)~图6(e)所示。 图6 台风特征统计检验图Fig. 6 Statistical test chart of typhoon characteristics 5.4台风诱发暴潮、巨浪与伴生的天文大潮统计分布诊断检验 台风诱发暴潮、巨浪与伴生的天文大潮统计分布诊断检验,如图7~图9所示。各图中圆点为实测资料点,实线为模型曲线;图(c)中外围两条曲线为模型95%置信区间。 按照表5及图6、图7中的台风特征概率统计分析,可使用基于MCEVD的随机模拟技术求解不同海区台风致灾因素的各种组合。经过图7~图9的台风诱发巨浪、暴潮及相应天文大潮的统计分布诊断检验,使用PNLTCEVD相应的公式和软件,即可获得表7所示岭澳核电站海区以巨浪为致灾控制因素的极端荷载组合,从而可对核安全规范制定的防护工程设计标准进行风险评估。 图7 台风暴潮诊断检验图Fig. 7 Distribution diagnostic testing of storm surge 图8 天文大潮诊断检验图Fig. 8 Distribution diagnostic testing of spring tide 图9 波高诊断检验图Fig. 9 Distribution diagnostic testing of wave height 特征值重现期/a1005001000风暴增水/m2.79+0.513.49+0.713.85+0.80天文大潮/m2.14+0.302.19+0.352.75+0.46波高/m6.6+0.37.3+0.67.9+0.8 该核电站按HAF0100规范的设计标准为[51]: 1)“设计基准洪水”(DBF)=可能最大台风暴潮+天文大潮=6.35 m; 2)相应最大波高=6.6 m。 双层嵌套多目标联合概率模式计算结果为: 1)500年联合重现期最大台风暴潮,天文大潮为4.20+2.54=6.74 m; 2)相应最大波高为7.9 m。 图10 天文大潮和风暴增水联合概率密度分布 Fig. 10 Probability density distribution of spring tide and storm surge 实例计算表明:使用MCEVD理论,计算取得500年一遇联合出现的波高、暴潮和天文大潮的组合,远远高于核岭澳电站按相应“可能最大”组合的设防标准。 据1952-2000年统计资料,秦山核电站附近乍浦、澉浦、盐官等地最大潮差达 7.26~9.00 m。针对秦山核电站海岸防波堤9.76 m高程,进行以天文大潮为控制因素的台风诱发极端外荷作用下核电站海岸防护工程设防标准联合概率风险分析,结果如图10~图12以及表8所示。 图11 天文大潮和风暴潮累积频率分布Fig. 11 Cumulative probability distribution of spring tide and storm surge 图12 1 000年一遇天文大潮、风暴潮和波高联合概率分布Fig. 12 Joint probability distribution of spring tide, storm surge and extreme wave height with 1 000 years joint return period 联合概率/a天文潮/m风暴潮/m波高/m1004.23.02.55005.03.53.010005.54.03.5 秦山核电站海岸防波堤高度9.76 m,低于100年一遇以天文大潮为控制因素的台风诱发风暴潮,波高极端外荷。 我国沿海多个核电站的防护工程设防标准仍然是采用仿照美国(NOAA) 的SPH、PMH的模式,使用“可能最大风暴潮”(PMSS)”、“设计基准洪水(DBF)”以及国际原子能工程机构(IAEA)规定的“可能最大洪水(PMF)”等方法确定,忽略了这些定义和计算中存在的各种不确定性因素以及各种极端海况联合出现的概率。以南海岭澳核电站和秦山核电站防护工程为例,使用MCEVD理论,计算得出的500年一遇联合出现的波高、风暴潮和天文大潮的组合,远远高于两个核电站按相应“可能最大”组合的设防标准。按照我国水利工程设计标准,重要工程都需采用2 000年至3 000年一遇校核值,国际核电组织IAEA新建议采用万年一遇的风暴增水、天文大潮和波高组合作为防灾标准,而上述核电站的“可能最大”组合,连采用MCEVD计算得出的五百年一遇设计标准都达不到。面对全球极端气候频发的趋势,建议对核电防护工程设防标准进行全面风险评估,以达到国务院核电站安全规划(2011-2020)提出的“必须按照全球最高安全要求”的规定。 致谢:衷心感谢谢世楞院士对本项研究的支持。 [1] LIU Y C, SANTOS A, WANG S M, et al. Tsunami hazards along Chinese coast from potential earthquakes in south China sea[J]. Phys Earth Planet In, 2007, 163:233-244. [2] IAEA-TECDOC-1341, Extreme external events in the design or assessment of nuclear power plants[S]. Vienna: IAEA, 2003. [3] IAEA-TECDOC-1487, Advanced nuclear plant design options to cope with extrenal events[S]. Vienna: IAEA, 2006. [4] IAEA. Probability safety analysis (PSA) of other external events than earthquake[R]. Nuclear Energy Agency, Committee on the Safety of Nuclear Installations, NEA/CSNI, 2009. [5] Design-basis flood estimation for site characterization at nuclear power plants in the United States of America[S]. U. S. NRC, 2011. [6] HAD 101/09, 滨海核电厂厂址设计基准洪水的确定[S]. 北京: 国家核安全局, 1990. (HAD 101/09, Determination of design basis flood level on coastal nuclear power plant site[S]. Beiing: National Nuclear Safety Administration of China, 1990. (in Chinese)) [7] HAD 101/11, 核电厂设计基准热带气旋[S]. 北京: 国家核安全局, 1991. (HAD 101/11. Design tropical cyclone for nuclear power plant[S]. Beiing: National Nuclear Safety Administration of China, 1991. (in Chinese)) [8] HAD 101, 滨海核电厂厂址选择安全规定[S]. 北京: 国家核安全局, 1991. (HAD 101, Regulations for selection of nuclear power plant site[S]. Beijing: National Nuclear Safety Administration of China. 1991. (in Chinese)) [9] LIU D F, MA F S. Prediction of extreme wave heights and wind velocities[J]. Journal of the Waterway Port Coastal and Ocean Engineering, ASCE, 1980, 106: 469-479. [10] LIU D F. Long term distribution of hurricane characteristics[C]//Proceedings of the Offshore Technology Conference. 1982: 305-313. [11] KIRBY W H, MOSS M E. Summary of flood-frequency analysis in the United States[J]. J Hydrology, 1987, 96: 5-14. [12] OCHI M K. Stochastic analysis and probabilistic prediction of random seas[J]. Adv. Hydro-Science, 1982, 13: 217-315. [13] LANGLEY R M, EL-SHAARAWI A H. On the calculation of extreme wave heights: A review[J]. Ocean Eng., 1986, 13(1): 93-118. [14] NAFFA M G, FANOS A M, ELGANAINY M A. Characteristics of waves off the Mediterranean coast of Egypt[J]. J Coast Res, 1991, 7(3): 665-676. [15] QUEK S T, CHEONG H F. Prediction of extreme 3 s gusts accounting for seasonal effects[J]. Structure Safety, 1992, 11(2): 121-129. [16] CHEONG H F. Estimation of the minimum pressure coefficient due to gusts[J]. Structure Safety, 1995, 17:1-16. [17] NAFFAA M G. Wave climate along the nile delta coast[J]. Journal of Coastal Research, 1995, 11:219-229. [18] LIU D F, WANG L P. Theory of multivariate compound extreme value distribution and its application to extreme sea state prediction[J]. Chinese Science Bulletin, 2006, 51(23):2926-2930. [19] LIU D F, PANG L, FU G, et al. Joint probability analysis of hurricane Katrina 2005[C]//Proceedings of the Intern. Offshore & Polar Eng. Conference (ISOPE2006). 2006: 74-80. [20] LIU D F, PANG L, Xie B T, et al. Typhoon disaster zoning and prevention criteria -A double layer nested multi-objective probability model and its application[J]. Science in China Series E, Technological Sciences, 2008, 51(7): 1038-1048. [21] CHOWDHURY A G, HUANG P, ERWIN J. Aerodynamic testing application of a full-scale facility for mitigating hurricane-induced coastal disasters[J]. Far East Journal of Ocean Research, 2009, 2(1):1-27. [22] LIU D F, SHI H D. Disaster prevention design criteria for the estuarine cities: new orleans and shanghai-the lesson from hurricane katrina [J]. Acta Oceanologica Sinica, 2006, 25(4):124-130. [23] 刘德辅,庞亮,史宏达. 卡特里娜飓风的启示——有关海岸和水利工程的风险分析[J].中国工程科学, 2007, 9(10):24-29. (LIU Defu, PANG Liang, SHI Hongda. The lesson from hurricane Katrina 2005—Risk analysis for coastal, offshore and hydraulic engineering[J]. Engineering Sciences, 2007, 9(10): 24-30. (in Chinese)) [24] LIU D F, XIE B T, LI H J. Study on the design flood volume of the three gorges project[J]. Journal of Hydrologic Engineering, ASCE, 2011, 16(1): 71-80. [25] LIU D F, PANG L, LI H J. Extreme value prediction of typhoon induced disasters[C]//Proceedings of the 2nd International Summit on Hurricanes and Climate Changes, Monograph of invited papers in Summit. 2009: Paper No.21. [26] LIU D F, JIANG Y P, SHI H D, et al. Uncertainty analysis of breakwater wave overtopping volume, wave forces and structure stability[C]//Proceedings of the ISOPE. 2006:387-392. [27] LIU T F, ZHOU Z G, SHI J G, Optimum design environmental criteria for platforms[C]//Proceedings of the Int. Conference on Behaviour of Offshore Structures (BOSS). 1988, 3:1483-1495. [28] SHI J G, LIU D F, WANG Z. The joint long-term distribution of design environmental factors for offshore structures multivariable probabilities and simulating method[J]. Acta Oceanologica Sinica, 1993, 12(3):465-474. [29] LIU D F, YANG Y C, WANG C, et al. Joint probability of environmental loads on marine structures[C]//Proceedings of the OMAE. 1995: 408-415. [30] LIU D F, DONG S, WANG C. Uncertainty and sensitivity analysis of reliability for marine structure[C]//Proceedings of the OMAE. 1996: 380-386. [31] LIU D F, LIU G L, WANG F Q. Risk assessment of coastal defense against typhoon attacks for nuclear power plants[C]// Proceedings of the ICAPP. 2011: 2484-2492. [32] LIU D F, LI H J, LIU G L, et al. Design code calibration of offshore, coastal and hydraulic energy development infrastructures[J]. WSEAS International Journal of Energy and Environment, 2011, 5(6):733-747. [33] LIU D F, LIU G L, LI H J, et al. Discussion on IAEA and China safety regulation for NPP coastal defense infrastructures against Typhoon/Hurricane Attacks[J]. World Journal of Nuclear Science and Technology, 2012, 2:114-123. [34] LIU G L,LIU D F, LI T F, et al. Joint probability prediction model of rainfall triggered landslides and debris flows[J]. Open Journal of Geology, 2012, 2(2): 103-110. [35] LIU D F, LI H J, SHI H D, et al. Natural disasters: prevention, risk factors and management[M]. USA: NOVA Science Publishers, 2012: 1-86. [36] LIU D F, SHI H D, LIU G L, et al. Risk assessment for nuclear power plants against natural disasters[M]. New York: NOVA Publisher, USA, 2015: 1-131. [37] LIU D F, PANG L, XIE B T. Typhoon disaster in China-prediction, prevention and mitigation[J]. Natural Hazards, 2009, 49(3): 421-436. [38] MITTAL A. Army corps of engineers: history of lake pontchartrain and hurricane protection project[R]. GAO-06-244T, 2006. [39] BEA R. Reliability assessment and management:lessons from hurricane Katrina[C]//Proceedings of the Offshore Mech. & Arc. Eng.. 2007: OMAE2007-29650. [40] 刘德辅, 史宏达,等. 中国沿海台风灾害区划、防台风标准应急制定、防台风应急评估标准制定[R]. 青岛: 中国海洋大学, 2008. (LIU D F, SHI H D, et al. Typhoon disaster prediction, prevention and guideline of emergency plan for China Sea Coasts [R].Qingdao: Ocean University of China, 2008. (in Chinese)) [41] LIU D F, LIU G L,WANG F Q, et al. Extreme sea hazards statistics and engineering application[C]//Proceedings of the International Conference OCEANS` 14 MTS/IEEE. 2014. [42] LIU D F, LIU G L,WANG F Q, et al. Risk assessment of design flood for three gorges dam[C]//Proceedings of the 6th International Conference on Larger Asian River. 2014. [43] 刘德辅,史宏达,王风清.对我国两种海堤规范设计波浪标准的风险分析[J]. 海洋工程, 2013, 31(3):70-76. (LIU Defu, SHI Hongda, WANG Fengqing, Risk analysis for coastal structure design criteria in China[J]. The Ocean Engineering, 2013,31(3):70-76. (in Chinese)) [44] MADSEN H, ROSBJERG D. The partial duration series method in regional index-flood modeling[J]. Wat Res Res, 1997, 33(4): 737-746. [45] RANARD B, LANG M. Use of a Gaussian copula for multivariate extreme value analysis: some case studies in hydrology[J]. Adv Wat Res, 2006(30): 897-912. [46] SHI D J, ZHOU S S. Moment estimation for multivariate extreme value distribution in a nested logistic model[J]. Ann Inst statist math, 1999, 51(2): 253-264. [47] TARANTOLA S, GIGLIOLI N, JESINGHAUS J, et al. Can global sensitivity analysis steer the implementation of models for environmental assessments and decision-making? [J]. Stochastic Environmental Research and Risk Assessment, 2002, 16: 63-76. [48] Marine risk assessment by Det Norsk Veritas, for the health and safety executive, offshore technology report[R]. 2001. [49] LIU D F, KONG L S, ZUO J C, et al. Stochastic-numerical model of tidal current field for Jiaozhou bay of Yellow sea[C]//Proceedings of the ISOPE. 2001:682-685. [50] 刘德辅,马逢时.极值分布理论在计算波高多年分布中的应用[J].应用数学学报, 1976,1:23-37. (LIU D F, MA F S. Theory of extreme value distribution and its application on long term distribution of wave heights[J]. Journal of Applied Mathematics, 1976, 1: 23-37. (in Chinese)) [51] 谢世楞. 核电厂海域工程的设计标准问题[J].港口工程, 2000(1): 6-9. (XIE S L. Design criteria for nuclear power plants in coastal areas[J]. J. Port Engineering, 2000(1):6-9. (in Chinese)) Discussion on safety regulations for NPP coastal defense LIU Defu, SHI Hongda, LIU Guilin, WANG Fengqing (Ocean University of China, Qingdao 266003, China) P753 A 10.16483/j.issn.1005-9865.2017.04.017 1005-9865(2017)04-0135-12 2016-11-14 国家自然科学基金资助项目(51379195) 刘德辅(1936-),男,四川成都人,教授,主要从事海洋工程防灾减灾研究。E-mail:liu@ouc.edu.cn
5 南海岭澳核电站防护工程设防标准的风险分析
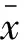
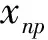

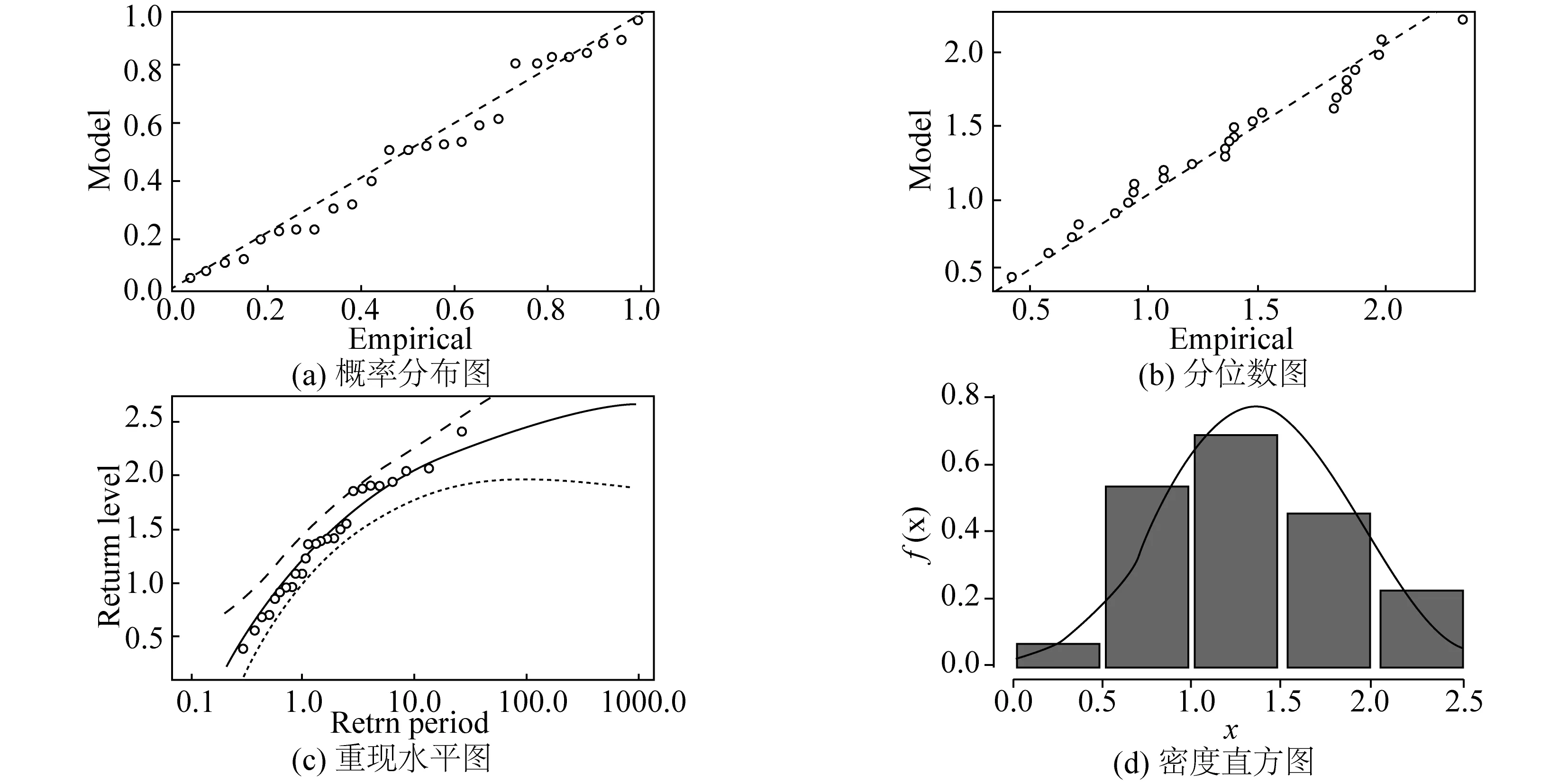

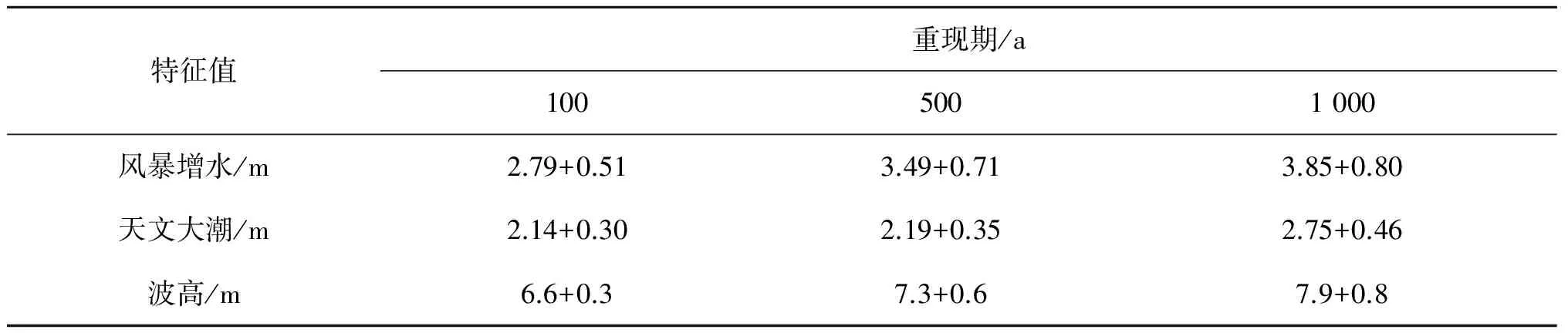
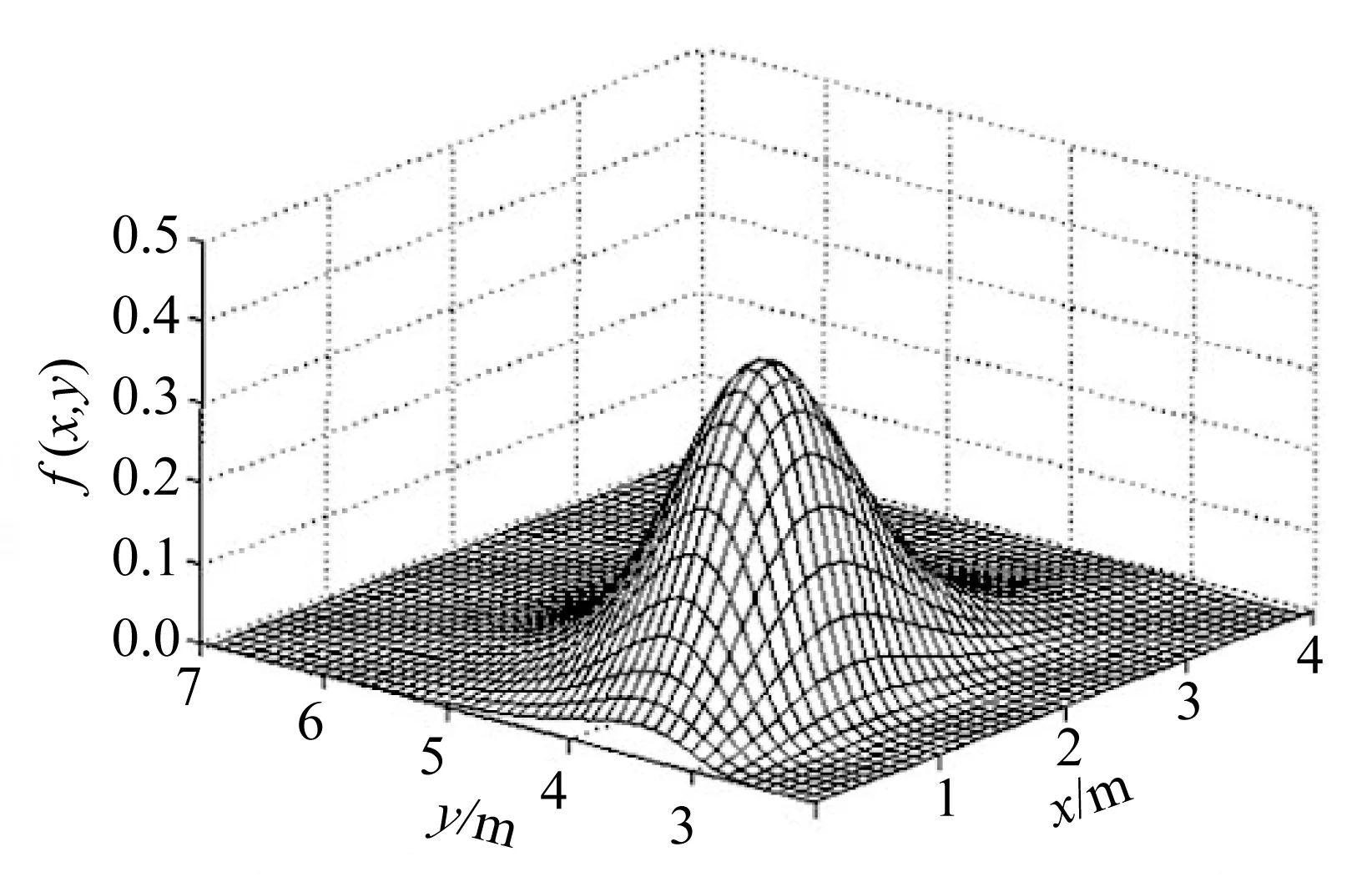
6 秦山核电站防护工程设防标准的风险分析
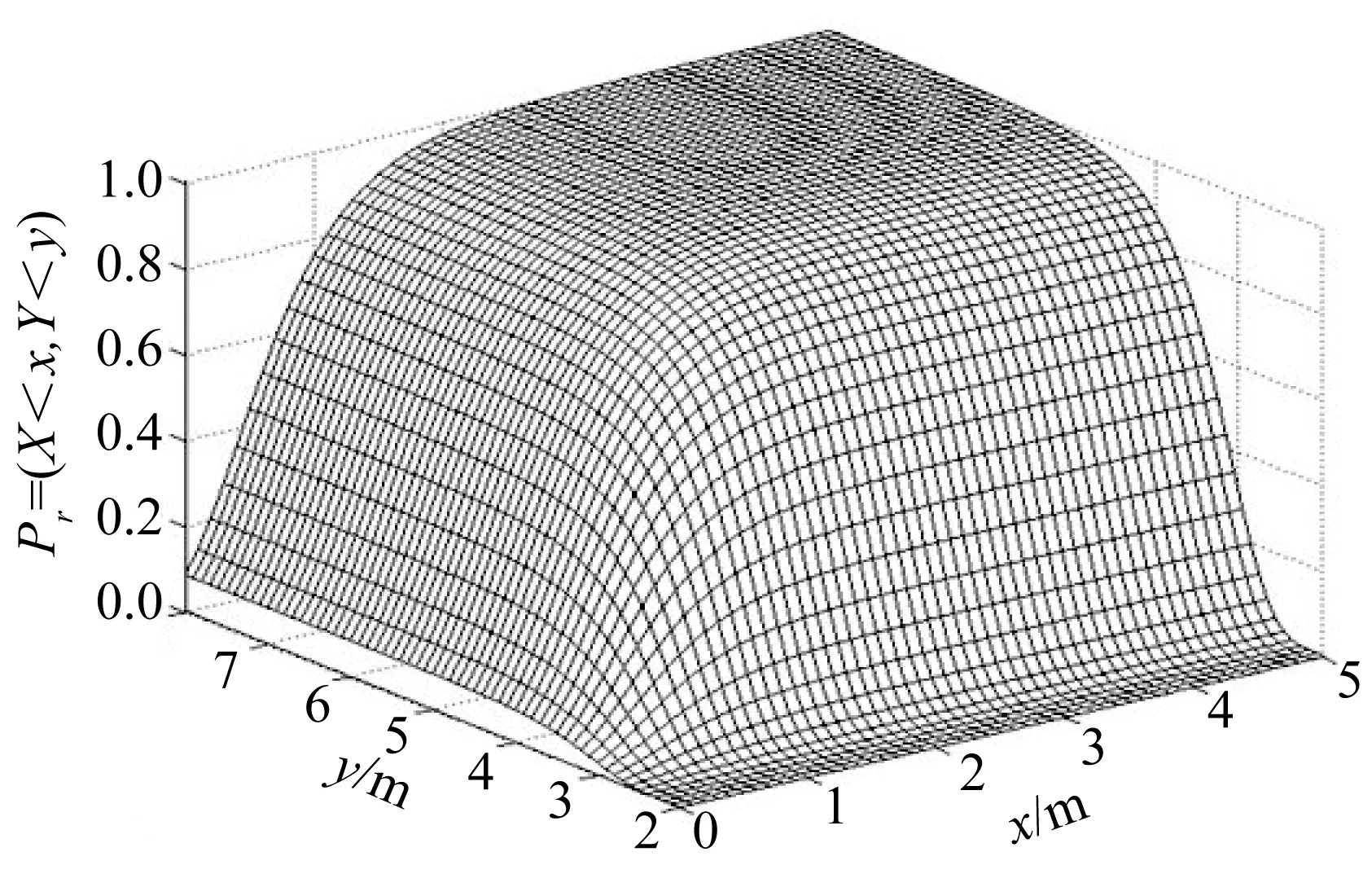

7 结 语
