内孤立波作用下FPSO动力响应特性

张瑞瑞，张新曙，尤云祥，许忠海，刘建成，王 晋

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240；2. 高新船舶与深海开发装备协同创新中心，上海 200240；3. 江苏科技大学，江苏 镇江 212000；4. 招商局重工(江苏)有限公司，江苏 海门 226116)

内孤立波作用下FPSO动力响应特性

张瑞瑞1，2，3，张新曙1,2，尤云祥1,2，许忠海1,2，刘建成4，王 晋1,2

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240；2. 高新船舶与深海开发装备协同创新中心，上海 200240；3. 江苏科技大学，江苏 镇江 212000；4. 招商局重工(江苏)有限公司，江苏 海门 226116)

以KdV、eKdV和MCC理论的适用性条件为依据，利用内孤立波产生的瞬时速度和瞬时压力沿船体表面求面积分的方法分别计算浮式生产储油卸油装置(FPSO)内孤立波摩擦阻力和Froude-krylov力，再结合时域有限位移运动方程，研究了有限深两层流体中的内孤立波与带分段式系泊缆FPSO的相互作用问题。以东沙群岛某海域实测170 m振幅的内孤立波为对象，数值分析了在内孤立波作用下FPSO的内孤立波动态载荷、运动响应及其系泊张力的变化特性。研究表明，内孤立波会对FPSO产生突发的冲击，使FPSO产生大幅度水平漂移运动，导致系泊缆张力显著增大。在该振幅内孤立波作用下，FPSO受到的水平力最大可达56 t，垂向力最大可达1 961 t；纵荡位移可达47.62 m，系泊缆张力增加最大可达106.4 t。因此，在FPSO等深海浮式结构物的设计应用中，内孤立波的影响是不可忽视的。

两层流体；FPSO；内孤立波；动力响应；系泊缆

Abstract: Based on the applicability conditions of KdV, eKdV and MCC theories, a theoretical model for analyzing the interaction characteristics of internal solitary waves with Floating Production Storage and Offloading(FPSO) connected to the sea floor by multi-component catenary mooring lines is presented by using coupled motion equations of the floating body in time domain, where the friction and Froude-Krylov forces on FPSO due to internal solitary waves are calculated with the integration of the instantaneous velocity and pressure by the wetted surface area of FPSO. The observed data near Dongsha Island are used as the characteristic parameters of internal solitary waves to simulate the variation characteristics of dynamic loads, motion responses and mooring tensions for FPSO，where the amplitude of the internal solitary has 170 m. It is showed that internal solitary waves will give rise to the sudden impact loads and motion responses for FPSO, as well as remarkable tension increases in catenary mooring lines. Under the interaction of such an internal solitary, the maximum value of the horizontal force for the FPSO can reach 56 t, the amplitude of the vertical force can reach 1 961 t, the displacement of the surge motion can reach 47.62 m, and the top-tension increment value for mooring line can reach 106.4 t. Therefore, the influence of internal solitary waves on the dynamic behaviors of deep-sea floating structure including FPSO cannot be neglected in the design and application.

Keywords: two-layer fluid; FPSO; internal solitary; dynamic response; mooring lines

我国南海深水海域油气资源丰富，已成为我国深海资源开发的主战场。作为深海油气开发中主流的浮式生产储油卸油装置(floating production storage and offloading,简称FPSO)，通常永久系泊于特定海域进行作业，其规避恶劣海洋条件的能力较差，海洋环境条件对其安全性和作业效率有很大影响，因此，研究其在各种海洋环境条件下的载荷及其动力响应等问题，对保证其安全性有重要的工程实践意义。

内孤立波是发生于密度分层海洋内部的一类特殊海洋波动现象，据大量海上测量和海洋遥感观测表明，南海内孤立波活动频繁，具有分布范围广、振幅大、持续时间长、诱导流场水平速度大等特点[1]。在内孤立波传播过程中诱导的水平流动，会使海洋结构物产生突发性的漂移运动，从而影响其正常的生产作业。在南海流花油田的早期延长测试期间，曾发生因内孤立波产生的突发性强流而导致缆绳拉断、船体碰撞，甚至拉断和挤破漂浮软管等事故。在南海陆丰油田的早期延长测试期间，也曾发生过内孤立波产生的突发性强流使半潜式钻井船与锚定油轮在连接输油管道时发生困难等问题[2]。可见，内孤立波已成为南海深海资源开发中必须考虑的海洋环境因素。

对密度层化海洋的处理，最简单的是两层模式，即把流体看作是密度均匀的两层，两层之间存在密度突变。常见的两层流体内孤立波理论有KdV (Korteweg-de Vries)、eKdV (extended KdV)和MCC (Miyata-Choi-Camassa)等理论模型来描述[3]。但在这三类理论中弱非线性和弱色散这两个条件仅为定性描述，为此黄文昊等[4]以系列实验为依据给出了这两个条件的定量表征方法。

在风浪流环境下，各类深水浮式结构物的载荷及其动力响应问题，目前已有较为成熟的理论方法。但在内孤立波环境下，各类深水浮式结构物载荷及其动力响应等问题，目前仍是海洋工程中面临的挑战性课题之一。Cheng等[5]和Cai等[6]将Morison公式与KdV理论结合，Xie等[7-8]将Morison公式与MCC理论结合，研究了内孤立波作用在小尺度杆件的载荷特性问题。王旭等[9-10]以三类内孤立波理论的适用性条件[4]为依据，采用N-S方程为流场控制方程，研究了内孤立波作用在半潜平台和张力腿平台的载荷特性问题。宋志军等[11]将Morison公式与KdV理论结合，研究了内孤立波作用下Spar平台的载荷与动力响应问题。尤云祥等[12-13]将Morison公式与eKdV理论结合，研究了内孤立波作用下张力腿和半潜式平台的载荷与动力响应问题。最近，黄文昊等[14]以三类内孤立波理论的适用性条件[4]为依据，结合文献[15]中建立的圆柱型结构内孤立波理论模型，研究了内孤立波作用下系泊Spar平台的内孤立波动态载荷及其动力响应问题。马孟达等[16]考虑三类内孤立波理论的适用性条件，结合浮体有限位移时域运动方程，采用Morison和Froude-Krylov公式计算张力腿平台的内孤立波动态载荷，建立了内孤立波与张力腿平台相互作用的理论模型，研究了内孤立波作用下典型张力腿平台(ISSC-TLP)动态载荷、运动响应以及张力腿张力的变化特性。而许忠海等[17]以系列实验为依据建立了FPSO的载荷理论预报模型。但内孤立波作用下FPSO的动力响应特性问题迄今尚不清楚。

有鉴于此，本文以三类内孤立波理论适用性条件为依据，利用文献[17]建立的FPSO内孤立波载荷计算方法，建立内孤立波与FPSO相互作用的理论模型。在此基础上，参照东沙群岛南部海域的内孤立波实测结果，研究分析在内孤立波作用下FPSO的动态载荷、运动响应及其系泊张力变化特性等问题。

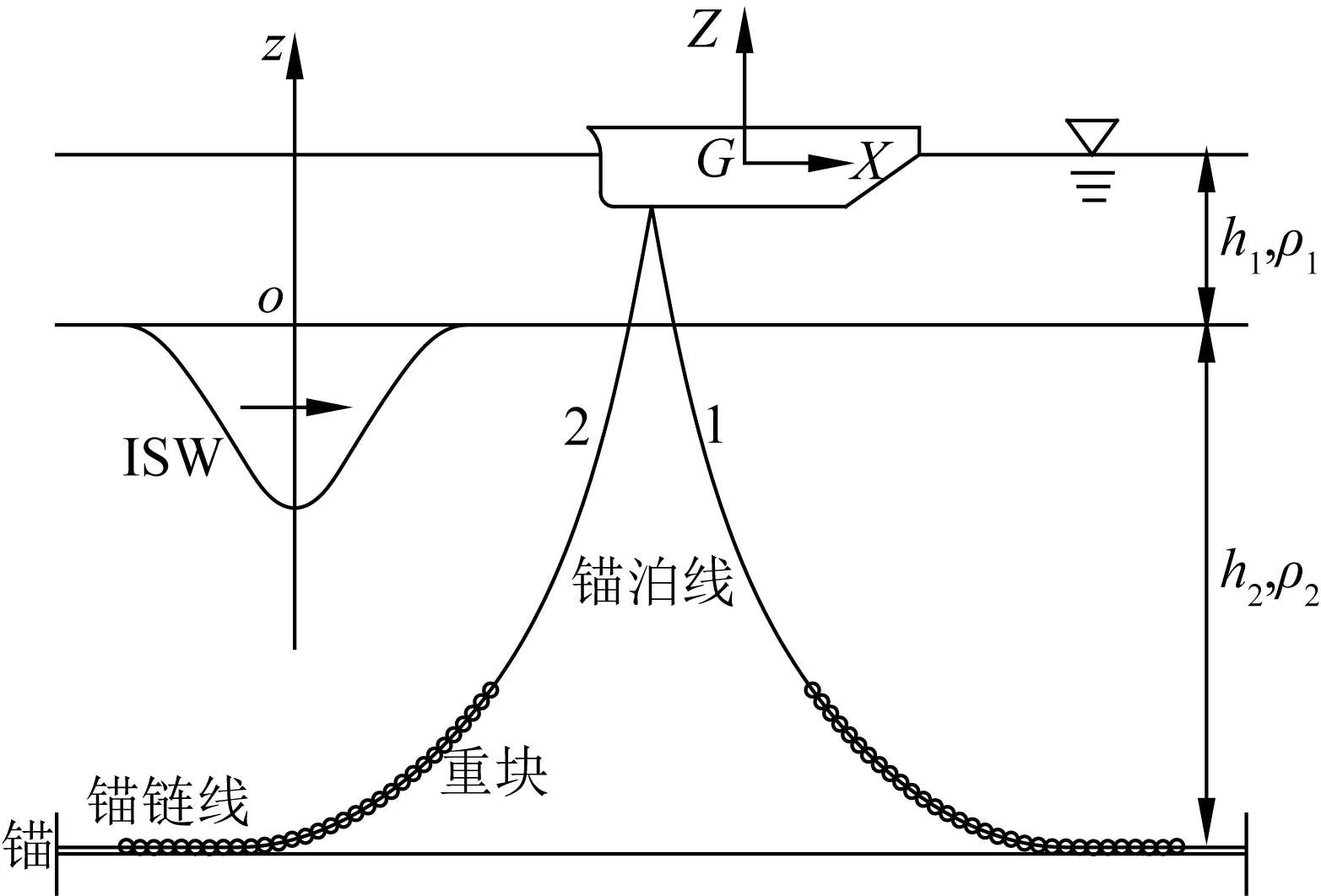
图1 FPSO及其坐标系Fig. 1 The sketch of FPSO and the coordinate system

1 数值方法

考虑有限深层流体中内孤波与FPSO的作用特性问题。设两层流体均为不可压缩且无旋的理想流体，在流体处于平衡状态时，上层流体深度与密度分别为h1和ρ1，下层流体深度与密度分别为h2和ρ2，总水深为h。为描述内孤立波特性，建立直角坐标系oxyz，其中oxy平面位于流体静止时两层流体的界面上，oz轴位于内孤立波波谷处，且垂直向上为正，如图1所示。

设FPSO的长度为LPP，宽度为B，吃水为d。系泊系统采用三段式悬链系泊缆，首尾两段为钢质缆，中间为重力压载链。为便于描述平台运动响应，记OXYZ为一个空间固定的坐标系。其中，坐标原点O位于FPSO静平衡时的重心G处，OXY平面与静水面平行，OZ轴铅直向上为正，OX轴正方向与内孤立波传播方向相同。记Gξηδ是固定在FPSO平台上的随体坐标系，当FPSO处于静平衡状态时，两个坐标系OXYZ与Gξηδ是重合的，如图1所示。

考虑内孤立波作用下FPSO在OXZ平面内的运动响应，其纵荡和垂荡位移分别用X1和X2表示，纵摇位移用X3表示。其中，X1和X2是重心G在OXYZ中的坐标，X3是Gξηδ相对于OXYZ的转角。

随体坐标系Gξηδ与固定坐标系OXYZ之间的坐标转换关系为

FPSO的3个自由度运动方程为：

式中：M为FPSO在工作状态时的质量，I为FPSO在工作状态时的纵摇惯性矩，Fi是FPSO受到的外力(i=1,2)和外力矩(i=3)，变量上方的点表示对时间的导数。

FPSO受到的外力与外力矩包括内孤立波作用力Fw及其力矩MGw，浮力FB及其力矩MGB，系泊传递力Fot及其力矩MGt，以及FPSO自身重力Mg。在求得这些力及力矩之后，即可确定外载荷Fi如下

式中：i,j,k是固定坐标系OXYZ的单位矢量；e1,e2,e3为随体坐标系Gξηδ的单位矢量；g为重力加速度。

1.1外载荷计算方法

首先给出FPSO内孤立波载荷的计算方法。坐标系OXYZ与oxyz之间的坐标转换关系为

式中：xd为波谷到FPSO重心的水平距离，hG为重心G到FPSO底部的距离。

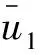
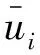
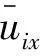
式中：

由伯努利方程可得，内孤立波在上下层流体中诱导的动压力为

为便于陈述，将上下层流体中的速度、动压力及密度统一写成如下形式

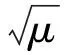
在实际海洋中，内孤立波的特征波长通常可达几百米甚至几千米，远大于FPSO的水平尺度，这意味着FPSO的存在对内孤立波特征的影响可以忽略。作用在FPSO上的Froude-Krylov力可利用内孤立波产生的瞬时压力，通过沿船体吃水表面直接求面积分计算[17]：

式中：S为FPSO船体的湿表面积；n为FPSO船体吃水表面的单位法向矢量,方向指向船体内部。

对内孤立波作用在FPSO上的摩擦阻力，可利用内孤立波产生的瞬时速度切向分量沿船体吃水表面直接求面积分计算[17]：

式中：τ为FPSO船体吃水表面的单位切向矢量,方向指向船体尾部；Vτ为FPSO船体吃水表面的切向速度；Cf为摩擦阻力系数。

由此可得，FPSO的内孤立波作用力Fw为

式中：Fwh和Fwv分别为水平力和垂向力。

对水平力和垂向力分别求其引起的力矩(以顺时针为正)为

式中：rGδ为Gξηδ中δ轴上的点(0,0,δ)相对于重心G的向量；rGξ为Gξηδ中ξ轴上的点(0,0,ξ)对于重心G的向量；L1和L2分别为重心到船尾和船首的距离；hG为重心G到FPSO底部的距离；hw为FPSO在流体中的瞬时浸没深度，其表达式为

当FPSO发生纵摇时，其浮力会对FPSO重心产生力矩，且在FPSO运动过程中，由于FPSO排水体积及其形状将发生改变，因此其浮心位置将会发生偏移现象。FPSO浮心位置在随体坐标系中的坐标变为

式中：ASξ为ξ处的横剖面面积；为排水体积；MξGη为排水体积对水线面ξGη的静矩。

FPSO的浮力为FB=ρg，当浮心发生偏移后，浮力对重心的力矩为

式中：rGB为浮心B相对于FPSO重心G的位置矢量；FGB为FB在随体坐标系中的相应矢量。

1.2系泊传递力计算方法

采用三段式悬链系泊缆，由锚链线、配重线和锚泊线组成，如图2(a)所示。其中，Wa，Wcl和Wc分别为它们的单位长度重量；Aa，Acl和Ac分别为它们的等效截面积；Ea，Ecl和Ec分别为它们的杨氏模量；H0和V0分别为系泊缆顶部的初始水平与垂向预张力；θ0为系泊缆的初始顶倾角；h0为系泊缆顶部导缆器到海底的距离。

设Ht和Vt分别为某一段系泊缆顶部的水平与垂向张力，Hb和Vb分别为其底部的水平与垂向张力，θt与θb分别为其顶倾角和底倾角，W与S分别为其拉伸后的单位长度的重量与长度，如图2(b)所示，那么其水平和垂向投影的悬链线方程为[19]

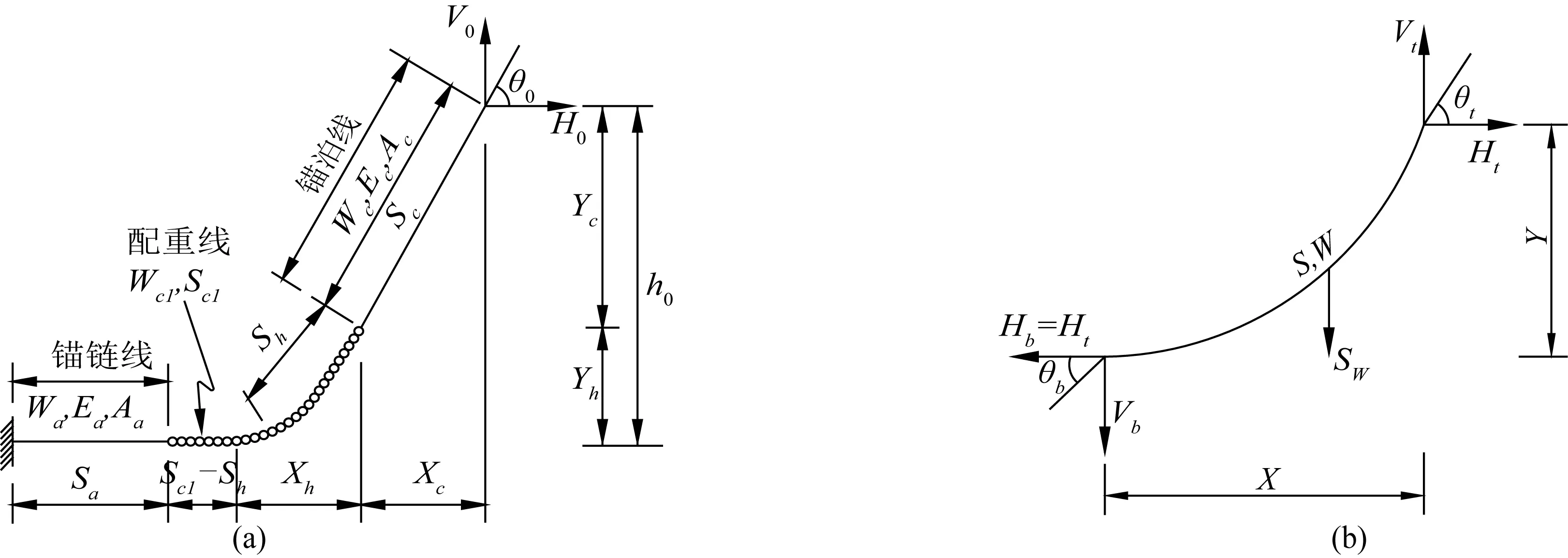
图2 分段式悬链线系泊缆Fig. 2 Multi-component mooring line

拉伸后分段系泊缆的长度和单位重量可按下式近似计算：

式中：S0为拉伸前分段系泊缆的长度；T0和T分别为拉伸前后分段系泊缆的平均张力；E和A分别为分段系泊缆的杨氏模量和等效截面积。

设FPSO的初始排水量为V，初始吃水为d，系泊缆顶端导缆器到FPSO船底的高度为hb，系泊缆顶部初始倾角为θ0，那么在静平衡时每根系泊缆的初始水平预张力H0与垂向预张力V0可表示为

根据式(20)～式(24)，采用迭代的方法，即可确定每根系泊缆的初始状态，之后通过改变系泊缆垂向顶张力，可获得系泊缆水平与垂向预张力与其顶部水平及垂向位移之间的响应曲面[20]。在此基础上，采用二维样条插值的方法，由系泊缆的顶部位移即可确定其顶部张力的水平与垂向分量，从而可得在任意瞬时系泊缆对平台的传递力及其力矩。

设δj和λj分别为在时刻t时第j根系泊缆导缆器Aj的水平及垂向位移，H(δj,λj)和V(δj,λj)分别为相应的水平与垂向张力，可分别由第j根系泊缆水平与垂向顶张力与其顶部水平及垂向位移之间的响应面通过插值获得。设FPSO处于静平衡状态时，第j根系泊缆导缆器Aj在固定坐标系中的坐标为(aj,0,bj)，则在时刻t时两根系泊缆水平和垂向位移为

对FPSO的系泊传递力为

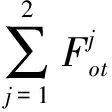
式中：j=1,2分别表示两根系泊缆。

由此可得，系泊传递力矩Mot为

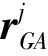
2 数值结果

根据Chang等[20]在东沙群岛南部海域的现场观测可知，上层流体深度h1=60 m，密度ρ1=1 022 kg/m3；下层流体深度h2=550 m，密度ρ2=1 025.5 kg/m3；观测到的内孤立波为下凹型波，最大振幅为a=-170 m。根据黄文昊等[4]对内孤立波理论适用性条件的分析，eKdV的理论极限振幅为amax=-128.3 m，该观测到的内孤立波已超出理论极限振幅，因此eKdV理论不适用。如果采用KdV理论，则在振幅a=-170 m下，经计算可得内孤立波的色散参数μ=1.125>μ0，由于KdV理论仅适用于弱色散情况，因此不适于表征本孤立波。如果采用MCC理论，则在振幅a=-170 m下，经计算可得内孤立波的色散参数μ=0.11>μ0，由于MCC理论不仅适用于强非线性的情况，而且也适用于强色散的情况，因此MCC理论适用于表征本孤立波。

表1 FPSO主要参数Tab. 1 Dimensions of the FPSO

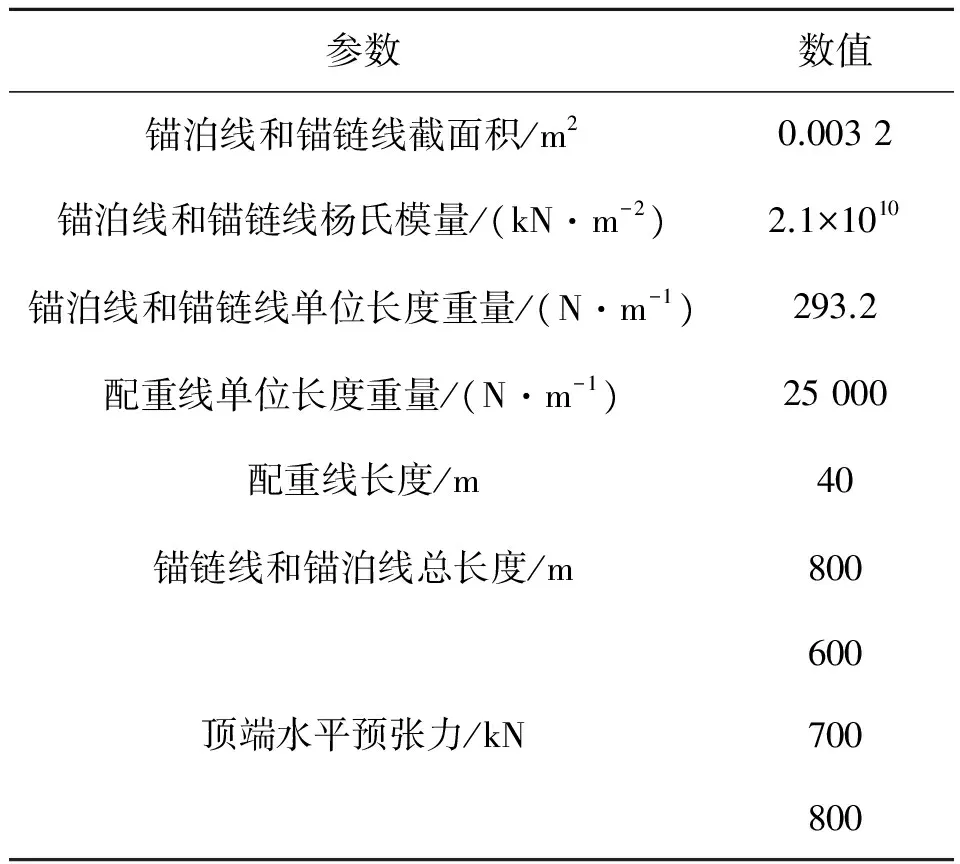
表2 分段式系泊缆主要参数Tab. 2 Data for multi-component catenary mooring line

表1给出了FPSO的主要参数，表2给出了分段式系泊缆的主要参数。假设系泊缆顶端水平预张力H0为600 kN时,其顶端角度θ0=60°,出于控制变量的考虑，其垂向预张力在不同水平预张力时均为1 039.2 kN。当水平预张力为600 kN时，在图3和图4分别给出了系泊缆水平和垂向顶张力与顶部水平/垂向位移之间的关系。由图可知，单根系泊缆的系泊力与顶部垂向位移的关系近似呈线性关系；而单根系泊缆的系泊力与顶部水平位移的关系则呈非线性特征，并且在水平位移为0处配重段部分悬起、部分躺底，系泊力由于水平位移的增大或减小而急剧增大或减小。因此，对FPSO与系泊动力响应的计算是非线性时域耦合的。利用图3和图4的结果，采用二维样条插值的方法，由系泊缆的顶部位移即可确定其顶部张力的水平与垂向分量，从而可得在任意瞬时系泊缆对FPSO的传递力及其力矩。

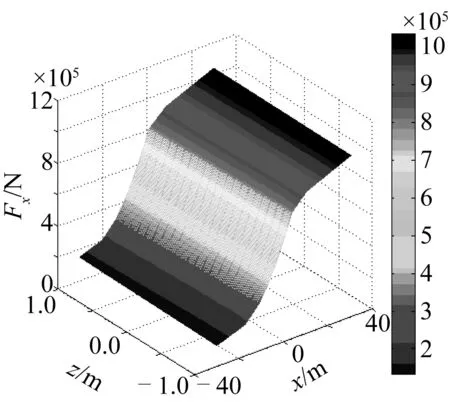
图3 当水平预张力为600 kN时，系泊缆水平顶张力与顶部水平/垂向位移之间的关系Fig. 3 Relationships between the horizontal force and the horizontal/vertical excursions of a single mooring line when horizontal tension equals 600 kN

图4 当水平预张力为600 kN时，系泊缆垂向顶张力与顶部水平/垂向位移之间的关系Fig. 4 Relationships between the vertical force and the horizontal/vertical excursions of a single mooring line when horizontal tension equals 600 kN

2.1载荷与动力响应时历特性

许忠海等[17]在系列实验基础上，获得了表1所述FPSO摩擦力系数的经验预报公式如下

根据式(29)，在图5中给出了当a=-170 m,h1:h2=6:55和水平预张力为600 kN时，内孤立波作用下FPSO载荷时历特性的数值结果。其中，左图为水平力时历，右图为垂向力时历。对水平力，经计算可得摩擦阻力系数为2.14e-5，由图可知，FPSO的摩擦力很小，可以忽略。结果表明，在东沙群岛海域实测大振幅内孤立波作用下，FPSO的水平力最大正值约为56 t，最大负值约为-55 t。从图中可以看出，在内孤立波波峰到达FPSO之前，其水平力先增大至最大值后减小为零；在内孤立波波峰过后，其水平力反向增大至最大值后减小。

由于FPSO船体底面积大，因此其垂向Froude-Krylov力很大，最大可达1 961 t，且始终为正值。原因在于FPSO始终位于上层流体中，而在上层流体中内孤立波诱导水平速度方向与其传播方向相同，流体动压力始终为正，因此FPSO的垂向力始终是正值。

图6给出了当a=-170 m和h1:h2=6:55，系泊缆顶端水平预张力为600 kN、700 kN、800 kN时，在内孤立波作用下FPSO运动响应时历特性的数值结果。由图可知，在东沙群岛海域实测大振幅内孤立波作用下，FPSO的纵摇响应很小，最大值为-7.85×10-4rad (纵摇角取顺时针为正)，可以忽略；FPSO垂荡响应主要表现为上升运动，最大上升量约为0.245 m；而内孤立波对FPSO纵荡响应的影响最为显著，当系泊缆顶端水平预张力为600 kN时，纵荡水平位移最大，最大正值可达29.6 m,最大负值可达47.62 m，而且在内孤立波经过后，仍出现幅值可达30余米的往复纵向运动现象。由此可见，系泊缆顶端水平预张力对FPSO纵荡响应的影响较大，对垂荡和纵摇响应的影响较小。为此，在下面的分析中，系泊缆顶端水平预张力均取600 kN。

图6 当a=-170m和h1:h2=6:55时,FPSO运动响应时历特性Fig. 6 Time histories for motion responses of FPSO when a=-170m and h1:h2=6:55

图7给出了当a=-170 m,h1:h2=6:55和水平预张力为600 kN时，在内孤立波作用下FPSO系泊缆张力增量时历特性的数值结果,其中ΔTot-1和ΔTot-2分别为两根系泊缆张力增量。由图可知，在东沙群岛海域实测大振幅内孤立波作用下，FPSO的系泊缆张力会发生急剧变化，对系泊缆1，其张力增加最大可达44.2 t，而张力减小最大可达86.4 t；对系泊缆2，其张力增加最大可达39.2 t，而张力减小最大可达106.4 t；在内孤立波经过FPSO之后，系泊缆张力还会出现较大幅度的震荡现象，对系泊缆1，其震荡幅值可达约70 t，而对系泊缆2，其震荡幅值可达约60 t。FPSO系泊缆顶端张力的这种大幅度突然变化现象，会导致系泊缆突然张紧和松弛的问题，从而对系泊系统的安全性产生严重的影响。

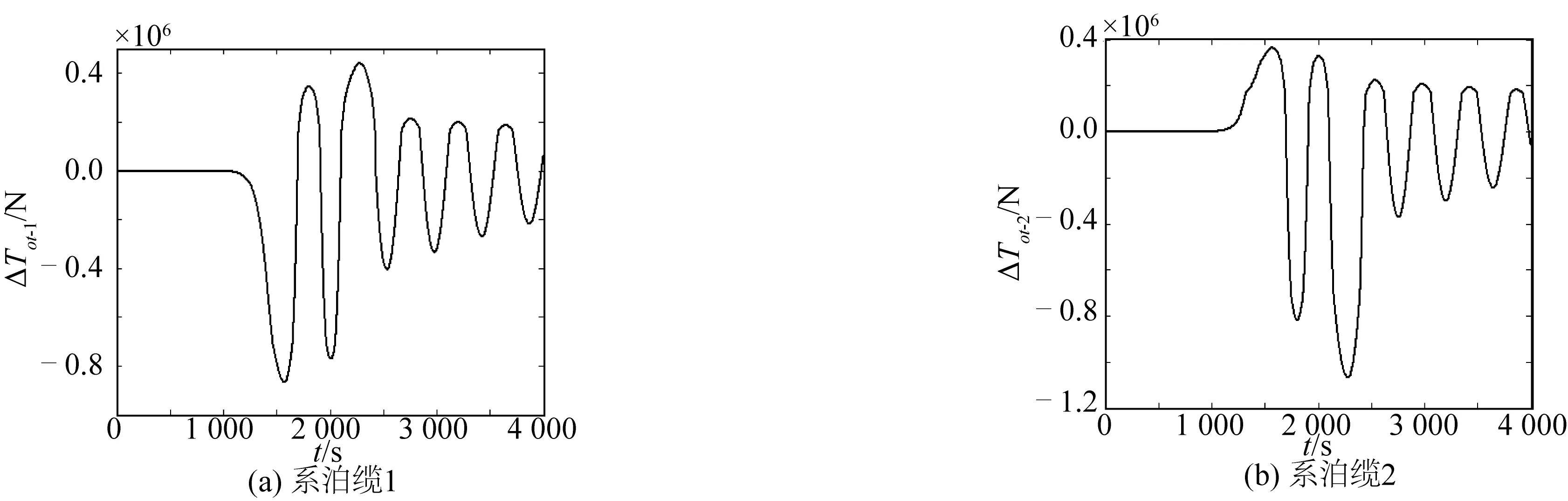
图7 当a=-170 m,h1:h2=6:55和水平预张力为600 kN时,FPSO系泊缆张力增量时历特性Fig. 7 Top-tension increment of mooring lines when a=-170m ,h1:h2=6:55 and horizontal tension equals 600 kN

2.2动力响应幅值变化特性

下面分析系泊缆顶部水平预张力为600 kN条件下,FPSO遭遇不同振幅内孤立波时的动力响应幅值变化特性问题。图8给出了当h1:h2=6:55时，FPSO运动响应幅值随内孤立波波幅变化特性的数值结果。其中，X1max为FPSO纵荡位移最大值，X2max为FPSO垂荡位移最大值。由于FPSO纵摇响应幅值很小，因此略去了其纵摇响应幅值的结果。结果表明，FPSO的运动响应幅值随内孤立波振幅的增大而增大；当内孤立波振幅小于130 m时，随着内孤立波增幅的增大，FPSO纵荡位移最大值近似线性增加；当振幅超过130 m后，随着内孤立波增幅的增大，FPSO纵荡位移最大值的增加出现变缓趋势；对垂荡位移，随着内孤立波增幅的增大，其最大值则近似线性增大。

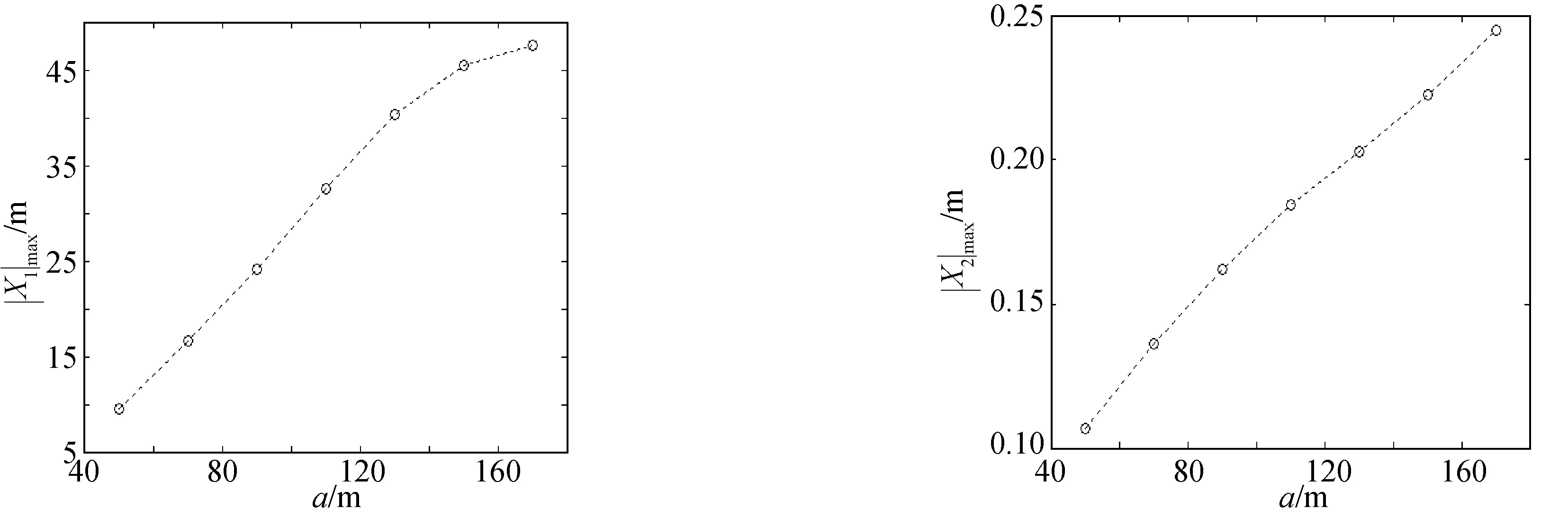
图8 当h1:h2=6:55时，不同振幅内孤立波下FPSO运动响应幅值变化特性Fig. 8 Variation characteristics of motion amplitudes of FPSO for internal solitary waves with different wave amplitudes when h1:h2=6:55

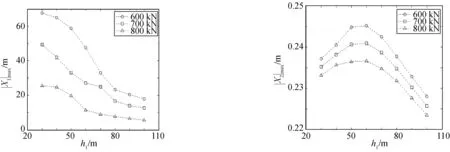
图9 当a=-170 m时，不同上层流体深度下FPSO运动响应幅值变化特性Fig. 9 Variation characteristics of motion amplitudes of FPSO for internal solitary waves with different wave amplitudes when a=-170 m

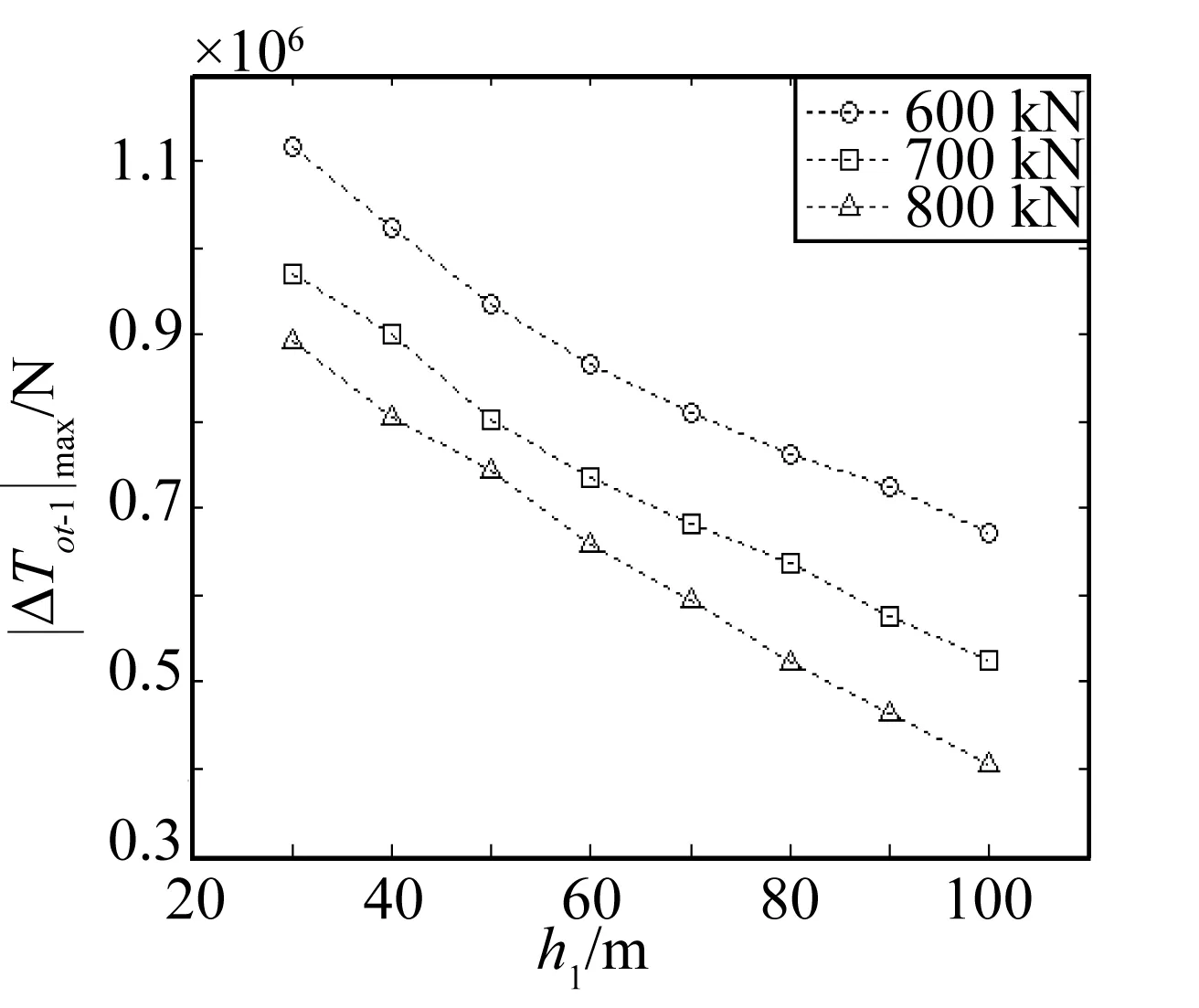
图10 当a=-170 m时，不同上层水深情况下FPSO系泊缆顶端张力变化幅值特性Fig. 10 Variation characteristics of top-tension increment for mooring lines with different upper-layer depth when a=-170 m

海水的跃层位置随着季节有明显的不同，在保持总水深610 m不变的情况下，分析不同跃层位置对FPSO运动响应幅值的影响。图9给出了a=-170 m时，FPSO运动响应幅值随上层流体深度变化的数值结果。结果表明，随着上层流体深度的增大，纵荡幅值逐渐减小，这是由于在相同振幅条件下，随着上层流体深度的增大，上层流体中内孤立波诱导水平速度减小，对FPSO的载荷作用也随之减小；而垂荡幅值先增大、后减小，这是由于在相同振幅条件下，随着上层流体深度的增大，内孤立波的相速度增加，而在上层流体中内孤立波诱导的垂向速度减小，由式(9)确定的内孤立波诱导动压力则先增大后减小，以Froude-Krylov力为主的垂向力也随之先增大后减小，因此垂荡幅值先增大后减小。

不同跃层深度对系泊缆张力变化也会产生不同的影响。下面给出系泊缆1顶端张力幅值随上层流体厚度的变化特性，结果如图10所示，其中a=-170 m。结果表明，随着上层流体深度的增大，FPSO纵荡位移最大值随之减小，系泊缆1 顶端张力变化的最大值也呈近似线性规律减小；此外对于同一水深情况，随着初始水平预张力的增大，系泊缆1顶端张力变化的最大值减小。

3 结 语

基于两层流体内孤立波理论的适用性条件，根据伯努利方程，采用内孤立波产生的瞬时速度和瞬时压力沿船体吃水表面直接求面积分的方法计算FPSO的孤立波动态载荷，结合浮体有限位移时域运动方程和悬链线系泊理论，建立了内孤立波与带悬链线系泊FPSO相互作用的耦合动力响应模型。对东沙群岛附近海域某振幅为170 m的实测内孤立波与FPSO相互作用问题进行了数值计算，获得FPSO动态载荷、运动响应以及系泊缆张力的变化特性。主要结果：

内孤立波对FPSO运动响应的影响主要表现为大幅度的水平漂移运动，当系泊缆顶端水平预张力为600 kN时，FPSO产生最大水平位移为47.62 m，系泊顶端张力增加幅值为106.4 t；本文研究的振幅为170 m的实测内孤立波特征波长约1 800 m，对FPSO产生显著影响的作用时间约25 min；随着内孤立波波幅的增大，FPSO纵荡响应也随之增大；随着上层流体深度的增加，FPSO纵荡响应及其系泊缆张力变化幅值则随之减小。

研究表明，在我国南海深海油气资源开发中，将内孤立波作为深海浮式结构物水动力性能分析与评估的一种重要因素有现实工程需要，本文为分析与评估内孤立波与FPSO相互作用特性提供了一种切实可行的方法。

[1] 方欣华，杜涛. 海洋内波基础和中国海内波[M]. 青岛: 中国海洋大学出版社, 2005.(FANG X H，DU T. Fundamentals of oceanic internal waves and internal waves in the China Seas[M].Qingdao: China Ocean University Press, 2005.(in Chinese))

[2] 陈景辉.南海流花11-1深水油田开发工程[J].中国海洋平台, 1996, 11(1): 43-46. (CHEN J H. The development of Liuhua 11-1 oilfield in South China Sea[J].China Offshore Platform, 1996, 11(1): 43-46. (in Chinese))

[3] HELFRICH K R，MELVILLE W K. Long nonlinear internal waves[J]. Annu. Rev. Fluid Mech., 2006, 38: 395-425.

[4] 黄文昊, 尤云祥, 王旭, 等. 有限深两层流体中内孤立波造波实验及其理论模型[J]. 物理学报, 2013, 62(8): 10.7498/aps.62.084705. (HUANG W H, YOU Y X, WANG X, et al. Wave-making experiments and theoretical models for internal solitary waves in a two-layeruid ofnite depth[J]. Acta Phys. Sin., 2013, 62(8): 10.7498/aps.62.084705. (in Chinese))

[5] CHENG Y L, LI J C, LIU Y F, et al. The induced flow field by internal solitary wave and its action on cylindrical piles in the stratified ocean[C]//Proceedings of the International Conference on Fluid Mechanics. 2004.

[6] CAI S Q, LONG X, WANG S. Forces and torques exerted by internal solitons in shear flows on cylindrical piles[J]. Applied Ocean Research, 2008, 30(1):72-77.

[7] XIE J, JIAN Y, YANG L. Strongly nonlinear internal soliton load on a small vertical circular cylinder in two-layer fluids[J]. Applied Mathematical Modelling, 2010, 34(8):2089-2101.

[8] XIE J S, XU J, CAI S. A numerical study of the load on cylindrical piles exerted by internal solitary waves[J]. Journal of Fluids & Structures, 2011, 27(8):1252-1261.

[9] 王旭, 林忠义, 尤云祥. 半潜平台内孤立波载荷特性数值模拟[J]. 船舶力学, 2015, 19(10):1173-1185.(WANG X, LIN Z Y, YOU Y X. Numerical simulation for the load characteristics of internal solitary waves on the semi-submersible platform[J]. Journal of Ship Mechanics, 2015, 19 (10) :1173-1185. (in Chinese))

[10] 王旭, 林忠义, 尤云祥. 张力腿平台内孤立波作用特性数值模拟[J]. 海洋工程, 2015, 33(5):16-23.(WANG X, LIN Z Y, YOU Y X. Numerical simulation for interaction characteristics of internal solitary waves with tension leg platform [J]. The Ocean Engineering, 2015, 33(5):16-23.(in Chinese))

[11] 宋志军, 勾莹, 滕斌, 等. 内孤立波作用下 Spar平台的运动响应[J]. 海洋学报, 2010(2): 12-19.(SONG Z J, GOU Y, TENG B, et al. The motion responses of a Spar platform under internal solitary wave[J]. Acta Oceanologica Sinica, 2010(2):12-19. (in Chinese))

[12] 尤云祥, 李巍, 时忠民, 等. 海洋内孤立波中张力腿平台的水动力特性[J]. 上海交通大学学报, 2010 (1): 56-61.(YOU Y X, LI W, SHI Z M, et al. Hydrodynamic characteristics of tension leg platforms in ocean internal solitary waves[J]. Journal of Shanghai Jiao Tong University, 2010, 44(1):12- 17. (in Chinese))

[13] 尤云祥, 李巍, 胡天群, 等. 内孤立波中半潜平台动力响应特性 [J]. 海洋工程, 2012, 30(2): 1-7.(YOU Y X, LI W, HU T Q, et al. Dynamic responses of a semi-submersible platform in internal solitary waves[J]. The Ocean Engineering, 2012, 30(2):1-7.(in Chinese))

[14] 黄文昊, 林忠义, 尤云祥. 内孤立波作用下Spar平台动力响应特性[J]. 海洋工程, 2015, 33(2):21-31.(HUANG W H, LIN Z Y, YOU Y X. Dynamic response characteristics of a spar platform under internal solitary waves[J]. The Ocean Engineering, 2015,33(2):21-31. (in Chinese))

[15] 黄文昊, 尤云祥, 王旭, 等. 圆柱型结构内孤立波载荷实验及其理论模型[J]. 力学学报, 2013,45(5): 1-13.(HUANG W H, YOU Y X, WANG X, et al．Internal solitary wave loads experiments and its theoretical model for a cylindrical structure[J]．Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(5): 1-13. (in Chinese))

[16] 马孟达, 尤云祥, 张新曙. 海洋内孤立波作用下张力腿平台动力响应特性[J]. 水动力学研究与进展:A辑, 2016, 31(2): 135-144.(MA M D, YOU Y X, ZHANG X S. Dynamic response characteristics of a tensionleg platform under internal solitary waves[J]. Chinese Journal of Hydrodynamics, 2016, 31(2): 135-144. (in Chinese))

[17] 许忠海, 尤云祥, 黄文昊, 等. FPSO 内孤立波载荷实验及其理论模型研究[J]. 水动力学研究与进展: A辑, 2014, 29(1):24-33.(XU Z H, YOU Y X, HUANG W H, et al. Experiments and theoretical model on the load characteristics of the FPSO in internal solitary waves[J]. Chinese Journal of Hydrodynamics, 2014, 29(1):24-33. (in Chinese))

[18] CAMASSA R, CHOI W, MICHALLET H, et al. On the realm of validity of strongly nonlinear asymptotic approximations for internal waves[J]. Journal of Fluid Mechanics, 2006, 549: 1-23.

[19] AGARWAL A K, JAIN A K. Dynamic behavior of offshore spar platforms under regular sea waves[J]. Ocean Engineering, 2003, 30(4): 487-516.

[20] CHANG M H, LIEN R C, YANG Y J, et al. Nonlinear internal wave properties estimated with moored ADCP measurements[J]. Journal of Atmospheric & Oceanic Technology, 2011, 28(28):802-815.

Dynamic response characteristics of FPSO in internal solitary waves

ZHANG Ruirui1, 2, 3, ZHANG Xinshu1, 2, YOU Yunxiang1, 2, XU Zhonghai1, 2, LIU Jiancheng4, WANG Jin1, 2

(1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China; 3. Jiangsu University of Science and Technology, Zhenjiang 212000, China; 4. China Merchants Heavy Industry (Jiangsu) Co., Ltd., Haimen 226116, China)

P751

A

10.16483/j.issn.1005-9865.2017.04.002

1005-9865(2017)04-0008-10

2016-05-26

国家自然科学基金资助项目(11372184)；国家重大基础研究计划973课题资助项目(2015CB251203-3，2013CB036103)；江苏省海门市"东洲英才"创新团队基金

张瑞瑞(1981-)，女，山西临汾人，博士研究生，主要从事船舶与海洋工程水动力研究。

尤云祥。E-mail：youyx@sjtu.edu.cn