临床化学检验中精密度、正确度、总误差和测量不确定度的讨论

张诗诗，王薇，赵海建，王治国

(1.北京医院 国家老年医学中心 卫生部临床检验中心/北京市临床检验工程技术研究中心，北京 100730；2.北京协和医学院研究生院，北京 100730)

·专家论坛·

临床化学检验中精密度、正确度、总误差和测量不确定度的讨论

张诗诗1,2，王薇1，赵海建1，王治国1,2

(1.北京医院 国家老年医学中心 卫生部临床检验中心/北京市临床检验工程技术研究中心，北京 100730；2.北京协和医学院研究生院，北京 100730)

在临床化学检验中，精密度和正确度是测量程序两大主要的性能特征，同时也是临床实验室方法确认和性能验证的重要内容。由Westgard提出的传统“总误差(total error，TE)”模型已在临床实践工作中应用了几十年，该模型通过线性相加将不精密度和偏移结合在一起。但TE模型无法覆盖影响测量结果准确度的所有因素，TE的表达未分别阐明随机误差和系统误差的大小，也无法反映系统误差和随机误差的关系。因此，另一模型即测量不确定度(measurement uncertainty，MU)模型受到了认可和标准化机构的推荐。MU模型分别评定不精密度和偏移引入的MU，并表达为围绕最佳估计值的区间，在该区间内真值以一定的概率出现。鉴于MU评定的复杂性，开发便捷的软件简化MU的计算，有利于促进临床实验室中MU的使用。

精密度；正确度；不精密度；偏移；总误差；测量不确定度；测量程序；方法确认；性能验证

在临床化学检验中，测量程序的性能直接关系到测量结果的质量，并且进一步影响临床决策的制定。因此，临床实验室在使用任一测量程序前均需要对其进行方法确认和/或性能验证。ISO 15189[1]条款5.5.1“测量程序的选择、验证和确认”中也对此进行了描述，提出了临床实验室对测量程序进行确认和验证以及评定测量不确定度(measurement uncertainty，MU)的要求。在方法确认和/或性能验证中，精密度(precision)和正确度(trueness)是必不可少的两大性能特征，通常分别以不精密度(imprecision)和偏移(bias)表示[2]。根据Westgard“总误差(total error，TE)”模型，TE是不精密度和偏移的线性和[3]，同一TE可由多种不同的不精密度和偏移结合而成，且不精密度和偏移的任意结合会产生相同的TE。因此，对于可接受的TE值，可能会隐藏其中某一组分不可接受的情况，而对于不可接受的TE值，可能对于发现和纠正其根本原因帮助不大。基于TE模型的局限性，且为了更好地描述测量结果与真值的关系，另一重要概念MU被认可和标准化机构提出并推荐。

1 精密度和正确度的概念

在临床化学检验中，测量程序的方法确认和/或性能验证通常集中于精密度和正确度。精密度，是“在规定条件下，对同一或类似被测对象重复测量所得示值或测得值间的一致程度”[4]，反映测量结果随机误差的大小，通常以不精密度表达，常用标准差(s)或变异系数(CV)表示。正确度，是“无穷多次重复测量所得量值的平均值与一个参考量值间的一致程度”[5]，反映测量结果系统误差的大小，通常用偏移来度量。偏移是系统测量误差的估计值[4]，是由一种或多种系统误差所引起的。

对于以上两个非常重要的性能特征，制造商提供的试剂说明书中通常只包含有关精密度的信息，但是一般没有或无法提供有关正确度的信息。因为根据CLSI EP05-A3[6]、EP15-A3[7]、WS/T 420-2013[8]和CLSI EP09-A3[9]等文件，精密度容易通过样品的重复测量来获得,但正确度的评价或偏移的估计则较为困难。偏移的估计需要与源自参考测量程序或参考方法的参考量值比较，但是在临床实验室的实践工作中，由于成本和技术等问题，不可能总是与参考方法比对。因此，一般与临床实验室已用的常规方法比对，估计的是评价方法和比对方法之间的偏差[10]。实验室也可以参加室间质量评价正确度验证计划，将测量质控品所得量值的均值与质控品的指定值比较，估计偏移。但除参考测量程序以外，使用其他比对方法需要注意干扰物质的影响和基质效应。

2 总误差的概念及特征

1974年，Westgard等[3]引入了TE的概念，规定TE是随机误差和系统误差的线性和，且表达式为：TE=z×s+bias。其中，s代表不精密度，是精密度的常用表示方式；bias代表偏移，是正确度的度量。TE的概念将精密度和正确度结合到一起并形成一个统一的表达式。在临床实验室中，TE有2个主要用途：(1)描述测量程序的性能或者在减去偏移之后，通过不精密度(标准差)对TE进行标准化以获得西格玛度量，用于与其他实验室比较；(2)制定性能规范，包括允许总误差、允许不精密度和允许偏移。

然而，该传统TE模型也存在许多局限性。第一，采用该模型获得的TE并非检验过程完整的TE[11]，如生物学变异、仪器和试剂变异[12]等影响测量结果准确度的因素，TE无法将其全部覆盖。确切地说，此处的TE指的是由分析过程所引起的总分析误差(total analytical error，TAE)，小于完整检验过程的随机误差和系统误差之和[11,13]。关于TE和TAE之间的差异，CLSI EP21[14]中有进一步的解释。Westgard在其近期的一篇文章中还将TE的定义修改为：TE=z×s+│bias│[15]。第二，根据TE的定义，对于给定的TE值，可以通过不精密度和偏移的线性相加来获得。因此，减少偏移能够抵消增加的随机误差，反之亦然。但TE的表达中并未分别阐明随机误差和系统误差的大小，也没有为终端用户(如临床医生)提供是否应该从报告结果中加上或减去一定数值的信息。第三，TE反映的是测量程序总体的性能，仅使用TE说明测量程序的性能规范，无法进一步了解测量结果不精密度和偏移之间的关系。由于已知的偏移会影响测量结果的评估和临床决策的制定，允许总误差虽然包含已知的偏移却通常未对其具体说明。TE虽然在表面上可以满足临床医生和实验室人员的需求，但其实用价值却非常有限。但由于任何一种模型都不可能将所有来源的误差模型化，并且Westgard的传统TE模型已涵盖了TE的大部分[11]，因此在提出更好的模型之前，大部分临床实验室依然愿意使用Westgard的传统TE模型来描述测量程序的总体性能。第四，在TE模型中，已知的TE需要分解成系统误差和随机误差，才能与其他因素造成的误差合并。这也体现了TE缺乏转换性[16]。

3 测量不确定度的概念及特征

基于传统TE模型的局限性，MU被提出并受到了认可和标准化机构的推荐。在临床化学检验中，测量的性能以及结果也可以用MU表达，其定义[16]是“根据所有信息，表征赋予被测量量值分散性的非负参数”，且通用形式是标准差。MU不关注“真值”的未知性，而是通过定义一个量值区间来表达量值不完整性的信息。MU包含测量程序中所有可能的不确定度来源，同时也要求把已知的偏移减少到可忽略或消除。偏移的消除会导致测量程序总(或“合成”)不确定度的增加，这是MU使用必须满足的先决条件，与TE模型对于已知偏移的保留明显不同。在计量学领域，采用定义良好的校准品和高计量学标准的测量程序，对无干扰成分影响且无基质效应的样品进行赋值，可以充分地降低偏移。在临床化学检验中，从校准品的定义到测量程序的计量学标准均不可能达到最佳条件，因此校准品溯源链的每次比对均有不确定度的增加。

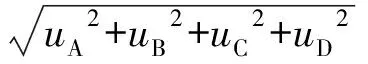
在医学实验室中，原则上有2种评定MU的方法[16]。第一种，“自下而上(bottom-up)”法，也称GUM或模型方法，是在全面系统地分析测量过程后，识别出每个可能的MU来源并通过统计学或其他方法(如从文献、产品说明书中获得性能数据)评定每个来源MU的大小，并使用方差法(各来源MU的方差和开平方)合并所有来源的MU以获得测量结果的“合成标准不确定度”。第二种，“自上而下(top-down)”法，这是临床实验室中较为经济实用的MU评定方法。在该方法中，精密度(不精密度/实验室内复现性)和正确度(偏移)是两个主要的分量，前者引入的MU可利用室内质量控制(IQC)数据、实验室间比对(PT)数据或重复测量常规样本的合并标准差来评定，后者引入的MU可利用有证参考物质(CRM)(包括正确度验证计划的质控品)、PT数据或与参考测量方法比较来评定，临床实验室通常将此二者与TE模型中的随机误差和系统误差相联系。若采用“自上而下”法获得的MU没有达到目标不确定度的要求，则可用“自下而上”法识别不确定度的各种来源，并有针对性地改进主要影响因素以减少MU。值得一提的是，不同于TE模型采用不同方式处理系统误差(各系统误差之和)和随机误差(先计算各随机误差平方和的平方根，再乘以包含因子k，通常k=1.96)，MU模型均采用同一方式处理评定过程中所有来源类型的MU组分，最终获得的MU也仅包含一种组分。

4 如何使用软件评估测量不确定度

MU评定过程的复杂性很大程度上阻碍了其在临床实验室中的发展和应用。如果可以设计软件并将计算过程编写成程序，那么实验室就能直接输入变量获得结果的MU。目前，已有专家学者开发出偏导数的数值逼近法[13]或模拟测量函数法[17]，在Microsoft Excel中对MU的计算编程。偏导数的数值逼近法设计的电子表格可以显示许多有用的信息，包括输入量值及其对应的绝对或相对标准不确定度计算后每个来源不确定度的相对大小、合成的绝对和相对不确定度以及扩展不确定度和其在给定置信水平的不确定度区间等。模拟测量函数法在电子表格中则很容易编程且可有几种算法用于模拟正态和其他的分布[18]。但这些方法也存在一些局限性，例如偏导数的数值逼近法并未解决共向变量以及指数或对数函数或者允许相同的输入量出现在测量功能的多个位置等问题。

介于MU评定算法的复杂性，用电脑编程和制作软件，发展MU评定的简便快捷方式，将是一个必然的发展趋势。若能改进现有方法并开发出更好的软件，不仅有利于临床实验室广泛使用MU，也可为临床医生制定决策提供有力的帮助。

5 总结

在临床化学检验中，精密度和正确度作为测量程序的两大性能特征，同时也是临床实验室方法确认和性能验证的重要内容。Westgard提出的传统TE模型通过线性相加将不精密度和偏移这两个独立的度量结合在一起，并创建出一个独立的表达式。然而，由于TE模型的局限性，其所能提供的信息无法满足临床实验室或临床医生的应用。因此，MU模型被提出以进一步描述测量程序的性能。MU模型除要求消除或减少偏移并用增加的合成不确定度代替，还可将已知的生物学变异、试剂变异等影响因素合并入MU的评定中。此外，开发简便快捷的MU评定软件可推动MU在临床实验室的广泛使用。

[1]ISO 15189. Medical laboratories—Requirements for quality and competence[S]. International Organization for Standardization, 2012.

[2]CNAS-CL38. 医学实验室质量和能力认可准则在临床化学检验领域的应用说明[S].中国合格评定国家认可委员会，2012.

[3]Westgard JO, Carey RN, Wold S. Criteria for judging precision and accuracy in method development and evaluation[J]. Clin Chem, 1974, 20(7): 825-833.

[4]JJF 1001-2011. 通用计量术语及定义[S]. 国家质量监督检验检疫总局，2011.

[5]王治国. 临床检验质量控制技术[M]. 第3版. 北京：人民卫生出版社，2014: 47-52.

[6]CLSI EP05-A3. Evaluation of precision of quantitative measurement procedures; approved guideline—third edition[S]. Clinical and Laboratory Standards Institute, 2014.

[7]CLSI EP15-A3. User verification of precision and estimation of bias; approved guideline—third edition[S]. Clinical and Laboratory Standards Institute, 2014.

[8]WS/T 420-2013. 临床实验室对商品定量试剂盒分析性能的验证[S]. 中国国家卫生和计划生育委员会，2013.

[9]CLSI EP09-A3. Measurement procedure comparison and bias estimation using patient samples; approved guideline—third edition[S]. Clinical and Laboratory Standards Institute, 2014.

[10]康凤凤，王治国. ISO 15189:2012与临床检验定量检测方法确认和性能验证[J]. 临床检验杂志，2013, 31(12): 881-884.

[11]Krouwer JS. The problem with total error model in establishing performance specifications and a simple remedy[J]. Clin Chem Lab Med, 2016, 54(8): 1299-1301.

[12]Krouwer JS. How to improve total error modeling by accounting for error sources beyond imprecision and bias[J]. Clin Chem, 2001, 47(7): 1329-1330.

[13]Kallner A. Is the combination of trueness and precision in one expression meaningful? On the use of total error and uncertainty in clinical chemistry[J]. Clin Chem Lab Med, 2016, 54(8): 1291-1297.

[14]CLSI EP21. Evaluation of total analytical error for quantitative medical laboratory measurement procedures—second edition[S]. Clinical and Laboratory Standards Institute, 2016.

[15]Westgard JO. Useful measures and models for analytical quality management in medical laboratories[J]. Clin Chem Lab Med, 2016, 54(2): 223-233.

[16]CNAS TRL-001:2012. 医学实验室—测量不确定度的评定与表达[S]. 中国合格评定国家认可委员会，2012.

[17]Farrance I, Frenkel R. Uncertainty in measurement: a review of Monte Carlo simulation using Microsoft Excel for the calculation of uncertainties through functional relationships, including uncertainties in empirically derived constants[J]. Clin Biochem Rev, 2014, 35(1): 37-61.

[18]Kallner A. Microsoft Excel 2010 offers an improved random number generator allowing efficient simulation in chemical laboratory studies[S]. Clin Chim Acta, 2015, 438(1): 210-211.

R446

A

2017-02-04)

(本文编辑王海燕)

10.13602/j.cnki.jcls.2017.09.01

张诗诗，1991年生，女，硕士研究生，研究方向：临床实验室质量管理。

王治国，研究员，E-mail: zgwang@nccl.org.cn。