基于小波变换的混凝土压缩损伤模式识别
2017-10-12王宗炼任会兰宁建国
王宗炼, 任会兰, 宁建国
(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
基于小波变换的混凝土压缩损伤模式识别
王宗炼, 任会兰, 宁建国
(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
为了实时获取混凝土中微裂纹扩展演化的物理信息,对实验采集的每一个声发射信号作小波变换,识别出3种典型模式的声发射信号;根据声发射信号的事件密度变化规律和脆性材料断裂理论,将混凝土压缩破坏过程分为微孔洞压缩闭合、裂纹萌生、裂纹生长和裂纹汇合4个阶段。根据混凝土材料中声发射信号频率与裂纹源尺寸呈反比例关系以及声发射信号在4个破坏阶段中的分布特征,将3种模式的声发射信号分别对应于裂纹萌生、裂纹生长和微孔洞压缩闭合、裂纹汇合。实验结果表明,裂纹萌生、裂纹生长和微孔洞压缩闭合、裂纹汇合对应的声发射信号的上升时间依次增长、频率逐渐降低,与应变能释放理论相符合。
固体力学; 混凝土; 声发射; 小波变换; 损伤机制
Abstract: In order to acquire the physical information about the evolution of microcraks in concrete in real time, three typical types of acoustic emission (AE) signals are identified by the wavelet transform of experimentally collected AE signals.The whole compressive fracture process of concrete is divided into four stages,i.e., microvoid compressive closure, crack initiation, crack growth and crack coalescence, on the basis of the event density fluctuation of AE signals andthe fracture theory of brittle materials. Based on the inverse proportional relationship between the frequency of AE signal and crack size, and the distribution characteristics of the three types of AE signals at four fracture stages, the AE signals are associated with crack initiation, crack growth (or microvoid compressive closure) and crack coalescence, respectively. The experimental results show that the rise times and frequencies of AE signals caused by crack initiation, crack growth (or microvoid compressive closure) and crack coalescence increase in turns and decrease gradually, respectively, which conform to the strain energy release theory.
Key words: solid mechanics; concrete; acoustic emission; wavelet transform; damage mechanism
0 引言
混凝土是一种典型的非均匀准脆性复合材料。微裂纹演化及汇合是准脆性材料的主要损伤机制。混凝土内部裂纹在形成和扩展时,局部源快速释放能量、产生瞬态弹性波,即声发射现象[1]。声发射信号可以提供材料内部微观缺陷产生和发展的动态信息,利用声发射信号的特点能够检测材料中裂纹产生、扩展汇合而导致材料断裂的动态过程。声发射技术作为一种成熟的无损检测方法,具有实时、动态、对结构影响小的优点,广泛应用于金属、陶瓷、岩石及复合材料的破坏失稳机理研究[2-8]。
很多学者在混凝土结构声发射检测方面做了大量工作,但是这些研究主要集中于幅值、事件数、振铃数、能量等参数的分析方法[9-15]。Iturrioz等[9]利用声发射技术监测混凝土棱柱试件在压缩载荷及预制裂纹梁在3点弯曲载荷下的破坏行为,同时采用网格模型模拟两种情况下混凝土的破坏过程,基于声发射数据分析(声发射信号幅值分布斜率b值、声发射事件率、能量)进行实验,结果与数值模拟结果吻合良好。朱宏平等[10]在混凝土损伤力学及声发射活性速率理论的基础上,建立了在单轴受压状态下混凝土材料的声发射特征参数与损伤演化间关系的方程,实现了运用测量得到的声发射特征参数最终量化评估混凝土的损伤大小。Sagar等[11]基于声发射参数如声发射事件率、能量、幅值和振铃数等参数的分析,对混凝土和水泥砂浆在3点弯曲载荷作用下破坏过程的不同阶段进行了研究。Corrado等[12]基于能量密度、声发射信号幅值分布斜率b值和重整化群理论评估单轴压缩情形下混凝土、岩石损伤区域分形维数,其中能量密度、声发射信号幅值分布斜率b值建立在声发射技术的基础上,3种方法的分析结果吻合良好。吴胜兴等[13]对混凝土轴拉破坏进行了声发射研究,实验结果表明:幅值、振铃、持续时间、声发射信号能量、绝对能量和信号强度6个参数能够较好地体现混凝土轴拉损伤过程的阶段性特征;幅值、振铃数、持续时间、上升时间和信号强度5个参数之间存在显著的相关性。Tsangouri等[14]对损伤的混凝土和自修复的混凝土中声发射源定位精度进行了研究,结果表明:声发射源定位误差可以表征裂纹演化阶段(微裂纹过渡到宏观裂纹)和损伤程度,可以作为混凝土裂纹的自愈合指标,然后通过管网供应愈合剂来修复裂纹。Gluth等[15]通过声发射技术对混凝土暴露在高温环境中及后续冷却过程中的剥落行为与裂纹演化进行了监测,根据声发射事件率变化判断危险裂纹的形成并分析了对应的微观结构变化。综上所述,参数分析法对于研究裂纹扩展量和材料损伤度具有重要意义,但对于材料细观损伤机制识别方面明显不足。
声发射信号具有瞬态性和随机性,包含不同频率和模式成分。已有学者发现,不同的损伤模式产生的声发射信号具有不同的频率特征[16-17]。采集到的声发射信号经过快速傅里叶变换能够得到信号的频谱图,但在变换过程中丢掉了时间信息,在处理非稳态声发射信号时存在明显的不足且很难定量、全面地分析信号特征。小波变换可以将单一时域信息变换为时间- 频率域信息,并可以将信号进行多尺度分解,在声发射信号处理中扮演着重要角色[18-20]。但目前较少有学者利用小波分析法对声发射信号与混凝土材料细观损伤机制之间的联系展开研究。
因此,本文采用声发射技术对混凝土压缩破坏过程进行实时监测。对采集到的每一个声发射信号进行小波分析,得到小波时频图与能量分布图,以识别3种典型模式的声发射信号。根据声发射信号的事件密度变化和脆性材料细观损伤理论,将混凝土压缩破坏过程分成4个阶段,即微孔洞压缩闭合阶段、裂纹萌生阶段、裂纹生长阶段和裂纹汇合阶段。然后根据混凝土材料中声发射信号与裂纹源尺寸的反比例关系和声发射信号的频率特征,以及声发射信号在4个破坏阶段中的分布特征,将第1种模式的声发射信号对应于裂纹萌生,第2种模式的声发射信号对应于裂纹生长和微孔洞压缩闭合,第3种模式的声发射信号对应于裂纹汇合。最后结合应变能释放理论对实验结果进行分析。
1 实验方法
实验中混凝试件尺寸规格为长100 mm×宽100 mm×高200 mm,混凝土材料制作配合比为水∶水泥∶砂子∶石子为0.52∶1.00∶2.23∶3.97. 粗骨料为石灰石碎石骨料,粒径为5~20 mm连续级配,细骨料为河砂(中砂)。混凝土采用电动式搅拌棒搅拌,由振动台振动密实,24 h后拆模,随即放入标准养护室养护,试件养护至28 d后进行实验。
实验加载设备为WAW-2000型液压式压力试验机,最大载荷200 t,可以进行实验载荷以及位移的控制,加载速率在0.05~150 mm/min范围内可调并保持良好的线性。采用轴向力控制加载,保持恒定加载速度,加载速率设定为10 kN/s. 采用美国PAC公司生产的PCI-2多通道声发射采集系统,声发射探头为压电式传感器,谐振频率为150 kHz,带宽为50~400 kHz. 采样频率设为1 MHz,波形长度设为2 k(2 048 μs),预触发长度设置为256 μs;撞击闭锁时间(为避免反射波或迟到波干扰而设置的关闭测量电路时间间隔)设置为2 000 μs,以使采集的每个声发射信号避免反射波和迟到波的干扰,只代表一次材料局部变化;噪声门槛值设为45 dB,以有效地减少噪声的影响;传感器与试件之间使用白凡士林进行耦合,用白色透明胶带固定在试件表面;8个前置端放大器分别连在8个传感器上,增益设为40 dB. 实验加载装置和传感器布置及声发射仪器分别如图1和图2所示。

图1 实验加载装置及传感器布置Fig.1 Experimental setup and sensor layout

图2 声发射仪器Fig.2 Acoustic emission instrument
2 小波变换理论
当一个函数ψ(t)∈L2(R)(其中L2(R)表示平方可积的实数空间)满足以下性质时:
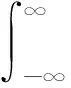
(1)

(2)
称函数ψ(t)为小波或母小波。将母小波ψ(t)经过尺度伸缩和时间平移后可得
(3)

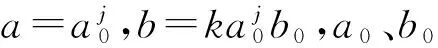
ψj,k(t)=2-j/2ψ(2-jt-k),j∈Z,k∈Z.
(4)
对于任意s(t)∈L2(R)的函数,关于离散小波基ψj,k(t)的离散小波变换(DWT)表达为

(5)
DWT的逆变换(重构公式)为
(6)
式中:c为常数。
信号的能量定义为
(7)
3 实验结果与讨论
3.1 声发射信号小波时频分析
为了研究声发射信号与混凝土材料细观损伤之间的联系,采用小波变换对采集的声发射信号进行处理,分析声发射信号的时频特性。
Daubechies小波基是小波变换中应用较广的一种小波,具有正交性和紧支撑性特征,而且可在频率域内快速衰减,因此Daubechies小波常用于分析处理采集到的声发射信号[17]。将Daubechies小波与采集到的声发射信号进行相似度比对,发现db3小波与采集的声发射信号最近似,故选择db3小波基对采集到的声发射信号进行小波分析。实验中,声发射的采样频率设定为1 MHz,根据Nyquist采样定理,采样频率必须为信号发生频率的2倍以上,因此采集的声发射信号的最大频率为500 kHz.

图3 3种典型模式的声发射信号波形(左)及小波时频图(右)Fig.3 Three typical waveforms (left) and corresponding time-frequency characteristics (right) acquired by wavelet transform
采集到的波形在第1 200个点之后的值极小,截取波形的前1 200个点(1 200 μs)对声发射信号进行波形和小波分析(见图3)。声发射信号经过小波变换得到时频图,将信号在时间和频率上的发展同时表现出来。从小波时频图上可以清楚地知道信号在某一时间点的频率成分,以及信号的某一频率成分出现的时间分布。
本文小波分析中选取的时间间隔为1 s,频率间隔1 kHz,信号长度为1 200 μs,小波时频分析的结果是由|cij|2(i=0,1,2,…,500;j=0,1,2,…,1 200)组成的矩阵。通过分析比较声发射信号的波形及时频特性,可以发现在混凝土压缩破坏过程中产生了3种典型模式的声发射信号。这3种典型声发射信号的波形和小波时频图如图3所示。
从图3中可以看出,第1种典型模式的声发射信号是一种突发型信号,具有较短的上升时间和持续时间。该信号能量主要分布在260~480 kHz频带上,并在(280 μs,460 kHz)处取得最大值,即信号的峰值频率为460 kHz,在280 μs处能量取得最大值。第2种典型模式的声发射信号呈现出突发型和连续型混合的模式,上升时间和持续时间相对于第1种有所增长。该信号的能量主要分布在15~250 kHz频带上,信号具有120 kHz和70 kHz两个峰值频率,分别在310 μs(能量为最大值)和475 μs(能量为仅次于最大值的极大值)时取得。第3种典型的声发射信号具有较长的上升时间和持续时间,是典型的连续型信号。该信号峰值频率为20 kHz, 能量主要分布在10~60 kHz频带上,并在330 μs处取得最大值。
3.2 声发射信号模式统计分析
对采集到的每一个声发射信号进行小波变换,8个通道的声发射信号特征整体相似,选取1号通道为研究对象。对采集的声发射信号按采集次序依次选取每20个声发射信号为一个窗口作为一组,计算每一种模式的声发射信号事件密度(窗口中某种模式的声发射数/20),计算结果表明:第2种模式的声发射信号事件密度在每个窗口均大于或等于0.3,根据3种模式的声发射信号事件密度变化,混凝土压缩破坏过程可以分成4段,图4(a)、图5(a)和图6(a)分别为试件1、试件2和试件3的分段结果。
具体的分段过程如下:1)损伤的初始阶段,第2种模式的声发射信号事件密度很大,达到0.8以上,第1种、第3种模式的声发射信号事件密度都很小;2)随着损伤的演化,第2种模式的声发射信号事件密度有所减小,第1种模式的声发射信号有所上升,当第1种模式的声发射信号事件密度上升至0.3以上且连续两个窗口的事件密度都大于或等于0.3时,破坏过程进入第2阶段;3)当第1种模式的声发射信号事件密度再次下降至0.3以下且连续两个窗口的事件密度都小于0.3时,破坏过程开始进入第3阶段;4)进入第3阶段后,第1种模式的声发射信号事件密度逐渐减小,直至为0,第2种模式的声发射信号事件密度有所增大,当损伤发展到一定程度时,第3种模式的声发射信号事件密度开始逐渐增大,当事件密度增大到0.3以上且连续两个窗口的事件密度都大于或等于0.3时,破坏过程进入第4阶段,第4阶段持续到试件最终的断裂失效。
3个试件在破坏过程中,3种模式的声发射信号累计声发射数变化如图4(b)、图5(b)和图6(b)所示;4个破坏阶段中每种模式的声发射信号含量百分比如图4(c)、图5(c)和图6(c)所示。

图4 试件1的分析统计结果Fig.4 Analytical and statistical results of Sample 1
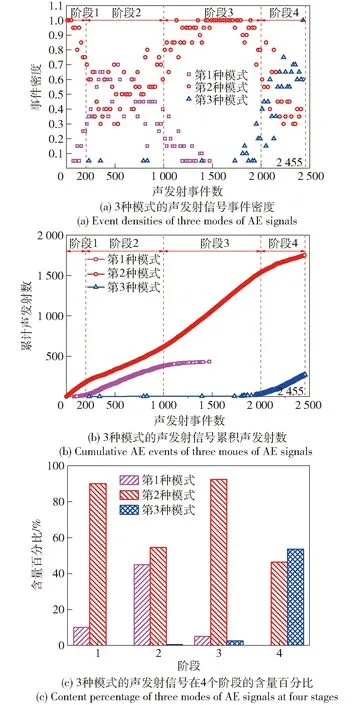
图5 试件2的分析统计结果Fig.5 Analytical and statistical results of Sample 2

图6 试件3的分析统计结果Fig.6 Analytical and statistical results of Sample 3
由以上3个试件的分析统计结果可以看出:在破坏过程的第1阶段,以第2种模式的声发射信号占主导,3个试件破坏过程的第1阶段中第2种模式的声发射信号含量百分比都高于80%,其他两种模式的声发射信号含量百分比都很小;进入第2阶段后,第2种模式的声发射信号含量百分比有所减小,第1种模式的声发射信号含量百分比明显增大,明显大于其他3个阶段中该模式的声发射信号含量百分比,第2阶段中第3种模式的声发射信号含量百分比仍然很小;第3阶段又是以第2种模式的声发射信号主导,试件1中该阶段第2种模式的声发射信号含量百分比为88%,试件2和试件3的该阶段中第2种模式的声发射信号含量百分比都高于90%;当损伤发展到一定程度时,第1种模式的声发射信号完全被抑制,第3种模式的声发射信号事件密度开始逐渐增大,当增大到一定程度时损伤进入第4阶段;第3种模式的声发射信号在第4阶段中占主导,3个试件破坏的第4阶段中第3种模式的声发射信号含量百分比均高于50%,远远大于其他3个阶段中该种模式的声发射信号含量百分比,在第4阶段,没有第1种模式的声发射信号产生。
3.3 实验结果分析
混凝土是一种由水泥砂浆、骨料和微缺陷组成的典型准脆性非均匀复合材料。根据脆性材料细观损伤理论[21],微孔洞压缩闭合、裂纹萌生、裂纹生长及裂纹汇合是准脆性材料损伤和失效的主要机制。由于混凝土试件在制作程中会产生原始微缺陷,在加载初期,这些微缺陷在压应力的作用下发生闭合并产生声发射信号。为了便于数学上的处理,常将准脆性材料中的初始微裂纹形状看作椭圆形[22]。当外载荷加载到一定程度时,椭圆型微裂纹尖端的应力强度因子满足裂纹扩展准则,在裂纹尖端某个方向上萌生出翼型裂纹。随着载荷的继续增大,翼型裂纹继续进行扩展、汇合直至材料最终的失效破坏[20]。图7为裂纹演化示意图,含裂纹的代表性单元受平面双轴载荷σ1、σ2的作用,椭圆形裂纹长轴与σ1的方向夹角为β,翼型裂纹成核扩展方向与椭圆形裂纹长轴夹角为ϑ. 声发射信号包含了材料局部变化的细观物理信息,每一个声发射信号都对应着某种特定的细观损伤机制。综上所述,可以判断3.2节中由声发射信号特征划分的4个破坏阶段分别对应微孔洞压缩闭合阶段、裂纹萌生阶段、裂纹生长阶段和裂纹汇合阶段。
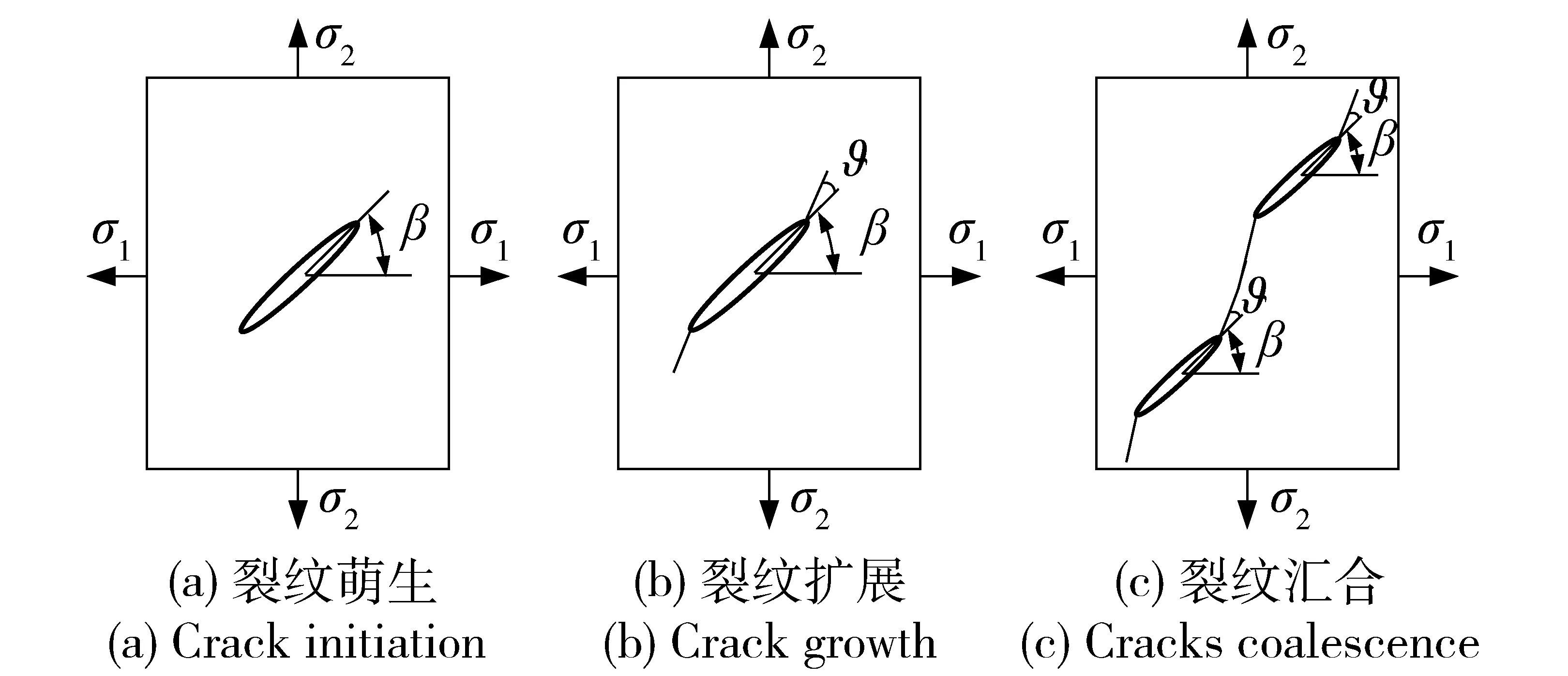
图7 裂纹演化示意图Fig.7 Schematic diagram of crack evolution
混凝土试件破坏后,对断口处进行电镜扫描,以更加清晰地观察和理解裂纹演化过程。断口处的电镜扫描图如图8所示。从图8(a)可以观察到裂纹在初始微缺陷处开始萌生,然后向周边区域扩展延伸;从图8(b)中可观察到翼型裂纹;图8(c)描述了两条即将发生汇合的扩展裂纹;从图8(d)中可以观察到3条不同扩展路径的裂纹发生了汇合,在裂纹汇合处附近分布着大量的微缺陷。

图8 混凝土断口不同位置处电镜扫描图Fig.8 SEM photographs of fracture surfaces of concrete
Haskell[23]和Ohnaka等[24]在研究地震波传播模型和地震波能谱密度时,证明了在膨胀或剪切断裂发生时,弹性波的频率f可简化为(8)式:
f~1/[T+(c/v)-(c/μ)cosθ] ,
(8)
式中:T为裂纹闭合、扩展或剪切变形时间;c为裂纹长度;v为裂纹扩展速度;μ为弹性波在介质内的传播速度;θ为弹性波传播方向与裂纹表面的夹角。为了研究裂纹长度和弹性波频率之间的关系,取θ=π/2 rad. (8)式可简化为
f~1/[T+(c/v)] .
(9)
通过以上分析发现,地质结构中裂纹闭合或张开时产生的弹性波频率与裂纹尺寸近似呈反比例关系,即更长的裂纹倾向于产生更低频率的弹性波。因此,混凝土作为人工合成的典型岩石类准脆性材料,其断裂过程中闭合或张开的裂纹尺寸与产生的声发射信号频率也呈反比例关系。
由3.1节的分析结果可知,第1种、第2种和第3种模式的声发射信号频率依次降低,说明第1种第2种和第3种模式的声发射信号对应的裂纹源尺寸依次增大。对每种模式的声发射信号在4个阶段的分布情况作进一步分析,结果如图9所示。
由图9可知,在3个试件中,每个试件破坏的整个过程所探测到的第1种模式的声发射信号中,都有超过80%的该种模式声发射信号分布在裂纹萌生阶段,而且由3.2节的实验结果可以看出第1种模式的声发射信号在裂纹萌生阶段的含量百分比明显高于其他3个阶段,由此可以判断出第1种模式的声发射信号对应于裂纹萌生。每个试件破坏的整个过程所探测到的第2种模式的声发射信号中,都有超过50%的该种模式声发射信号分布在裂纹生长阶段,而且3个试件中第2种模式的声发射信号在裂纹生长阶段的含量百分比都超过了85%,由此可以判断第2种模式的声发射信号对应于裂纹生长。第3种模式的声发射信号主要集中在裂纹汇合阶段产生,试件1中第3种模式的声发射信号在第4阶段中的分布比例超过了50%,试件2和试件3中第3种模式的声发射信号在第4阶段中的分布比例都超过了80%,而且每个试件的裂纹汇合阶段中第3种模式的声发射信号含量百分比都超过了50%,远远大于其他3个阶段中的含量百分比,由此可以判断出第3种模式的声发射信号对应于裂纹汇合。在3个试件中,微孔洞闭合阶段中第2种模式的声发射信号含量都超过了80%,因此微孔洞压缩闭合所产生的声发射信号也对应于第2种模式的声发射信号。
根据应变能释放理论[25],材料内部发生局部变化时释放应变能的强度与破坏源周围介质的弹性刚度有关,类似于弹簧反弹过程。
裂纹扩展面运动时间函数D(t)的上升时间τ与裂纹源邻域介质的弹性刚度K呈反比,即

(10)
由此可见,裂纹源扩展演化时,释放的应力波上升时间与裂纹源邻域介质的弹性刚度呈反比,裂纹源邻域的弹性刚度越小,释放应力波的上升时间越长。
弹性回弹引起的裂纹扩展面运动所释放的能量:
E~KD2(t),
(11)
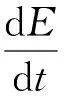
(12)
由此可见,裂纹扩展演化释放能量的快慢即应力卸载速率与裂纹源邻域介质的弹性刚度呈正比。应力卸载速率决定了裂纹扩展演化释放的应力波频谱,应力卸载速率越快即能量释放越快,释放应力波的频率越高。
实验中识别出的裂纹萌生、裂纹生长和微孔洞压缩闭合、裂纹汇合所对应的声发射信号的上升时间依次增长、频率依次降低。这是因为随着微裂纹的演化扩展,裂纹尖端邻域的刚度逐渐弱化[22, 26],裂纹扩展演化释放的应力波上升时间逐渐增长、频率逐渐降低。
4 结论
1)本文通过对采集的每个声发射信号进行小波变换和统计分析,识别出3种典型模式的声发射信号,根据3种不同模式的声发射信号事件密度变化和脆性材料断裂理论,将混凝土压缩破坏过程分成微孔洞压缩闭合阶段、裂纹萌生阶段、裂纹生长阶段和裂纹汇合阶段4个阶段。当破坏进入裂纹汇合阶段时,一些相邻的裂纹发生汇合,形成危险裂纹,材料处于临界失稳破坏状态,此时材料需全面检测后方可使用,据此可以对材料结构进行风险分析及寿命评估。
2)根据混凝土材料中声发射信号与裂纹尺寸的反比例关系和3种模式的声发射信号频率特征,以及3种模式的声发射信号在4个破坏阶段中的分布特征,3种典型模式的声发射信号分别对应于裂纹萌生、裂纹生长和微孔洞压缩闭合、裂纹汇合所产生的声发射信号。实验中裂纹萌生、裂纹生长和微孔洞压缩闭合、裂纹汇合所对应的声发射信号的上升时间依次增长,频率依次降低,这一结果与应变能释放理论相符合。
References)
[1] 杨明纬. 声发射检测[M]. 北京:机械工业出版社,2010. YANG Ming-wei. Acoustic emission testing [M]. Beijing: China Machine Press, 2010. (in Chinese)
[2] Woo S C, Kim J T, Kim J Y, et al. Correlation of fracture processes and damage mechanisms of armor structural materials under high strain rates with acoustic emission characteristics [J]. International Journal of Impact Engineering, 2014, 63:29-42.
[3] Perfilyev V, Lapsker I, Laikhtman A, et al. Scratching of copper and silicon: acoustic emission analysis[J]. Tribology Letters, 2017, 65(1):24-33.
[4] 褚亮, 任会兰, 龙波,等. 陶瓷材料破坏过程中的声发射源定位方法[J]. 兵工学报, 2014, 35(11):1828-1835. CHU Liang, REN Hui-lan, LONG Bo, et al. Location of acoustic emission of ceramics fracturing [J]. Acta Armamentarii, 2014, 35(11):1828-1835. (in Chinese)
[5] 王其胜, 万国香, 李夕兵. 动静组合加载下岩石破坏的声发射实验[J]. 爆炸与冲击, 2010, 30(3):247-253. WANG Qi-sheng, WAN Guo-xiang, LI Xi-bing. Acoustic emission experiment of rock failure under coupled static-dynamic load [J]. Explosion and Shock Waves, 2010, 30(3):247-253. (in Chinese)
[6] 杨班权,张坤,陈光南,等.涂层断裂韧性的声发射辅助拉伸测量方法[J].兵工学报,2008,29(4):420-424. YANG Ban-quan, ZHANG Kun, CHEN Guang-nan,et al. An acoustic emission-based uniaxial tensile test method for evaluation of fracture toughness of a coating on its substrate [J]. Acta Armamentarii,2008, 29(4):420-424.(in Chinese)
[7] Carvelli V, D'Ettorre A, Lomov S V. Acoustic emission and damage mode correlation in textile reinforced PPS composites [J]. Composite Structures, 2017, 163:399-409.
[8] 周伟, 孙诗茹, 冯艳娜,等. 风电叶片复合材料拉伸损伤破坏声发射行为[J]. 复合材料学报, 2013, 30(2):240-246. ZHOU Wei, SUN Shi-ru, FENG Yan-na, et al. Acoustic emission behavior on tensile failure of composite for wind turbine blades [J]. Acta Materiae Compositae Sinica, 2013, 30(2):240-246.(in Chinese)
[9] Iturrioz I, Lacidogna G, Carpinteri A. Acoustic emission detection in concrete specimens: experimental analysis and lattice model simulations [J]. International Journal of Damage Mechanics, 2013, 23(3):327-358.
[10] 朱宏平, 徐文胜, 陈晓强,等. 利用声发射信号与速率过程理论对混凝土损伤进行定量评估[J]. 工程力学, 2008, 25(1):186-191. ZHU Hong-ping, XU Wen-sheng, CHEN Xiao-qiang, et.al. Quantitative concrete-damage evaluation by acoustic emission information and rate-process theory [J]. Engineering Mechanics , 2008, 25(1):186-191. (in Chinese)
[11] Sagar R V, Prasad R V, Prasad B K R, et al. Microcracking and fracture process in cement mortar and concrete: a comparative study using acoustic emission technique[J]. Experimental Mechanics, 2013, 53(7):1161-1175.
[12] Carpinteri A, Corrado M, Lacidogna G. Three different approaches for damage domain characterization in disordered materials: fractal energy density,b-value statistics, renormalization group theory [J]. Mechanics of Materials, 2012, 53:15-28.
[13] 吴胜兴, 王岩, 李佳,等. 混凝土静态轴拉声发射试验相关参数研究[J]. 振动与冲击, 2011, 30(5):196-204. WU Sheng-xing, WANG Yan, LI Jia, et al. Parameters of acoustic emission test of concrete under static uniaxial tension [J]. Journal of Vibration and Shock, 2011, 30(5):196-204.(in Chinese)
[14] Tsangouri E, Karaiskos G, Deraemaeker A, et al. Assessment of acoustic emission localization accuracy on damaged and healed concrete[J]. Construction & Building Materials, 2016, 129:163-171.
[15] Gluth G J G, Rickard W D A, Werner S, et al. Acoustic emission and microstructural changes in fly ash geopolymer concretes exposed to simulated fire[J]. Materials and Structures, 2016, 49(12):1-12.
[16] Gutkin R, Green C J, Vangrattanachai S, et al. On acoustic emission for failure investigation in CFRP: pattern recognition and peak frequency analyses[J]. Mechanical Systems and Signal Processing, 2011, 25(4): 1393-1407.
[17] Koshida N, Hippo D, Mori M, et al. Characteristics of thermally induced acoustic emission from nonporous silicon device under full digital operation [J]. Applied Physics Letters, 2013, 102(12): 123504-123504-4.
[18] Sause M G R, Müller T, Horoschenkoff A, et al. Quantification of failure mechanisms in mode-I loading of fiber reinforced plastics utilizing acoustic emission analysis [J]. Composites Science and Technology, 2012, 72(2): 167-174.
[19] Karimi N Z, Minak G, Kianfar P. Analysis of damage mechanisms in drilling of composite materials by acoustic emission [J]. Composite Structures, 2015, 131:107-114.
[20] Ning J G, Chu L, Ren H L. A quantitative acoustic emission study on fracture processes in ceramics based on wavelet packet decomposition [J]. Journal of Applied Physics, 2014, 116(8):084901-084901-8.
[21] 冯西桥. 脆性材料的细观损伤理论和损伤结构的安定分析[D]. 北京:清华大学, 1995. FENG Xi-qiao. Micro-failure theory for brittle materials and shakedown analysis of structures with damage [D]. Beijing: Tsinghua University, 1995. (in Chinese)
[22] 宁建国, 任会兰, 方敏杰. 基于椭圆形微裂纹演化与汇合的准脆性材料本构模型[J]. 科学通报, 2012,57(21):1978-1986. NING Jian-guo, REN Hui-lan, FANG Min-jie. A constitutive model based on the evolution and coalescence of elliptical micro-cracks for quasi-brittle materials [J]. Chinese Science Bulletin, 2012, 57(21):1978-1986. (in Chinese)
[23] Haskell N A. Total energy and energy spectral density of elastic wave radiation from propagating faults[J]. Bulletin of the Seismological Society of America, 1964, 54(6A): 1811-1841.
[24] Ohnaka M, Mogi K. Frequency characteristics of acoustic emission in rocks under uniaxial compression and its relation to the fracturing process to failure[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1982, 87(B5): 3873-3884.
[25] Mitiyasu Ohnaka. A physical basis for earthquakes based on the elastic rebound model[J]. Bulletin of the Seismological Society of America, 1976, 66(2):433-451.
[26] Rodríguez P, Arab P B, Celestino T B. Characterization of rock cracking patterns in diametral compression tests by acoustic emission and petrographic analysis[J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 83:73-85.
IdentificationofDamageModesofConcreteunderCompressiveLoadingBasedonWaveletTransform
WANG Zong-lian, REN Hui-lan, NING Jian-guo
(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)
TB303.2
A
1000-1093(2017)09-1745-09
10.3969/j.issn.1000-1093.2017.09.011
2017-01-20
国家自然科学基金项目(11390363、11572049);北京理工大学爆炸科学与技术国家重点实验室自主课题项目(YBKT16-16)
王宗炼(1990—),男,博士研究生。E-mail: zonglianw@163.com
任会兰(1973—),女,教授,博士生导师。E-mail: huilanren@bit.edu.cn
