基于核密度估计的履带车辆传动轴载荷谱编制
2017-10-12刘海鸥张文胜徐宜赵梓烨
刘海鸥, 张文胜, 徐宜, 赵梓烨
(1.北京理工大学 车辆传动国家重点实验室, 北京 100081; 2.中国北方车辆研究所, 北京 100072)
基于核密度估计的履带车辆传动轴载荷谱编制
刘海鸥1, 张文胜1, 徐宜2, 赵梓烨1
(1.北京理工大学 车辆传动国家重点实验室, 北京 100081; 2.中国北方车辆研究所, 北京 100072)
为了建立军用履带车辆传动轴典型路面上的高可靠性载荷谱,通过实车试验采集接近实际使用情况的扭矩载荷及相关行车数据,由最少测试次数判据计算出载荷数据样本的置信度。由于试验载荷数据具有不规则的均幅值二维分布,基于二维核密度估计设计编谱流程,采取2次雨流计数,第1次雨流计数结果用于均幅值极值推断,第2次雨流计数结果用于核密度估计,既能很好地拟合均幅值分布,又能对实测雨流矩阵做合理外推。在获得典型路面使用寿命里程的二维设计载荷谱后,通过等损伤转换方法,将二维谱转化为以幅值为变量的8级程序块谱,并给出传动轴扭矩和转速的联合加载方法。研究结果表明,从疲劳损伤角度选择低载,舍去阈值为第8级幅值的0.8倍,频次和减少99.33%而损伤和只减少0.29%,可加速疲劳加载试验。
兵器科学与技术; 车辆传动; 载荷谱; 核密度估计; 疲劳分析
Abstract: For establishing the high reliability load spectrum for transmission shaft of military tracked vehicle on the typical road, the torque and relevant vehicle data similar to that in real service conditions was collected through vehicle experiments, and the confidence level of load data samples was calculated based on the criteria of least testing times. A load spectrum compiling procedure is designed based on 2-D kernel density estimation on account of the irregular 2-D distribution of amplitude and mean values in test load data. In the load spectrum compiling procedure, two times of rain-flow counting are adopted: the first rain-flow counting result is used to deduce the extrema of amplitude and mean values, and the second rain-flow counting result is used to extrapolate the kernel density. This compiling procedure can not only obtain better fitting of amplitude and mean distribution, but also achieve the reasonable extrapolation of the experimental rain-flow matrix. Goodman equation and the equivalent damage conversion method are used to derive 8-level program block load spectrum from 2-D load spectrum, and a loading method for the combination of torque and rotational speed is presented. 0.8 times of eighth amplitude are chosen as the value of small load from the perspective of fatigue damage, and total cycles are decreased by 99.33% while total damage is decreased only by 0.29%, which can accelerate the fatigue loading test.
Key words: ordnance science and technology; vehicle transmission; load spectrum; kernel density estimation; fatigue analysis
0 引言
载荷谱是进行车辆受载零部件机械结构设计和疲劳试验的基本依据,获得符合实际使用情况的载荷谱是车辆零部件抗疲劳设计的重要前提[1]。由于载荷循环包含幅值和均值两个维度,能反映材料力学特性的双参数雨流计数法,已成为现今载荷谱编制过程中通用的计数方法[2]。基于典型任务的对数当量寿命概率分布,阎楚良等[3]提出具有高置信度的中值疲劳载荷谱编制原理,提高了飞机结构定寿和延寿的可靠性。文献[4-5]分别在军用履带车辆传动装置耐久性评价与疲劳寿命预测方面做了相关研究。在对雨流矩阵做概率分布拟合时,与传统参数法相比,非参数法的拟合效果更具优势,其中核密度估计法得到越来越多的研究和应用[6-9],但其与编谱流程的有机结合则较少被关注。
军用履带车辆的传动装置、行走装置、行驶路面和驾驶操作有别于一般车辆,这些特点使其行驶载荷复杂多变,传动系零部件发生疲劳破坏的故障率高,故编制可信度较高的传动系定寿载荷谱,对车辆的可靠性提升具有重要意义。本文以某型履带车辆传动轴为例,选择一种典型行驶路面,首先通过实车试验测得接近实际使用情况的载荷数据样本,由最少测试次数判据计算样本数据的置信度;然后基于二维高斯核密度估计提出一种新的编谱流程,生成该路面设计使用寿命的多工况二维载荷谱;最后运用疲劳损伤等效方法建立8级程序谱,并从疲劳损伤角度选择低载舍去阈值,可加速疲劳加载试验。
1 载荷数据获取与处理
1.1 测试车辆和试验方法
某型履带车辆的传动系统为综合传动装置,为了测量其传动轴的扭矩载荷,扭矩传感器布置在左侧减速器的输入轴上(见图1),通过粘贴电阻应变片和无线遥测来获取扭矩信号。同时,为了监测车辆的行驶状态,还同步测量了发动机转速、传动轴转速和挡位等信号。
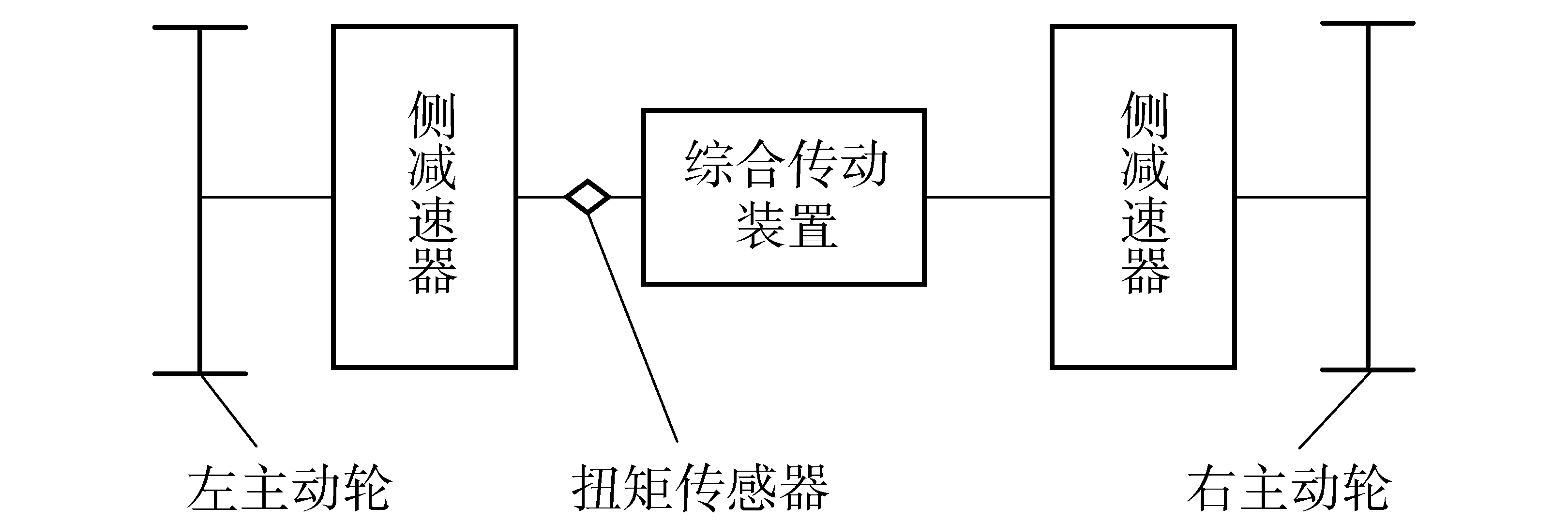
图1 扭矩传感器布置位置Fig.1 Mounting position of torque sensor
车辆可以明显地以路面和挡位划分典型工况,不同路面和挡位下的载荷频率、大小和序列有显著区别[10]。本文采集载荷数据的典型路面选择环形起伏土路,由3名经验丰富的驾驶员完成12圈试验,车辆的挡位分配和换挡频率完全由驾驶员根据路面情况和驾驶习惯所决定。在驾驶员随机驾驶的情况下包含了车辆起步、加速、制动、直行、转弯等各种工况,因此以每圈试验得到的载荷数据作为随机样本,可用于推测起伏土路上履带车传动轴的载荷统计特性。
1.2 数据采集与预处理
恶劣的试验条件会对测试系统造成一定干扰,同时扭矩信号具有瞬变特性,测试时不可避免地引入了对载荷谱编制不利的成分。本次试验中原始载荷数据的不良成分主要为高频噪声,高频噪声表现为频次很高、幅值很小的载荷循环,其对传动轴的疲劳寿命几乎不会产生影响[11],但是对编谱和疲劳加载是不小的负担,为最大程度地保留造成疲劳损伤的载荷循环,高频噪声将在雨流计数后去除。
2 置信度检验
在疲劳可靠性设计中,主要以典型工况载荷时间历程的计数结果作为样本的统计特征[12-13]。本文由每圈试验统计得到的对数当量寿命作为统计量,通过最少测试次数判据检验样本量的置信度[3]。
由载荷时间历程计数得到的载荷循环对应一定的疲劳损伤。设传动轴的当量使用寿命为L,与传动轴所承受的疲劳损伤呈负相关关系。根据Palmgren-Miner线性累积损伤准则,疲劳损伤D可量化为
(1)
式中:ni为各级载荷水平Si作用下的载荷循环次数;Ni为各级载荷水平Si单独作用下的极限循环次数;i=1,2,…,k. 令当量使用寿命为疲劳损伤的倒数,即

(2)
采用疲劳载荷处理TecWare软件计算出12圈扭矩数据的伪损伤[14-15],用于代替实际损伤,可简化最少测试次数的计算过程。然后由(2)式计算出当量寿命L,进而得到对数当量寿命lgL,如表1所示。经检验,本次试验的对数当量寿命以95%置信度服从正态分布。

表1 载荷样本对数当量寿命计算
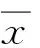
(3)

取置信度γ=80%,相对误差限度δ=5%,求得n=8.1,取整为9,即在该环形起伏土路上载荷试验的最少测试次数为9次,计算过程如表2所示。因为实际测试圈数为12>9,所以根据统计理论可知,

表2 最少测试次数计算
当以本次试验的平均对数当量寿命作为母体均值的估计量时满足80%置信度,相对误差不超过±5%.
3 二维载荷谱的生成
3.1 载荷循环统计计数
在载荷数据的计数环节中,雨流计数法是公认的有效方法,其中又以4点法最为常用[2]。将采集的随机扭矩和车速数据按不同挡位切割,将相同挡位的扭矩和车速连接到一起。扭矩T数据按挡位的统计结果如表3所示。
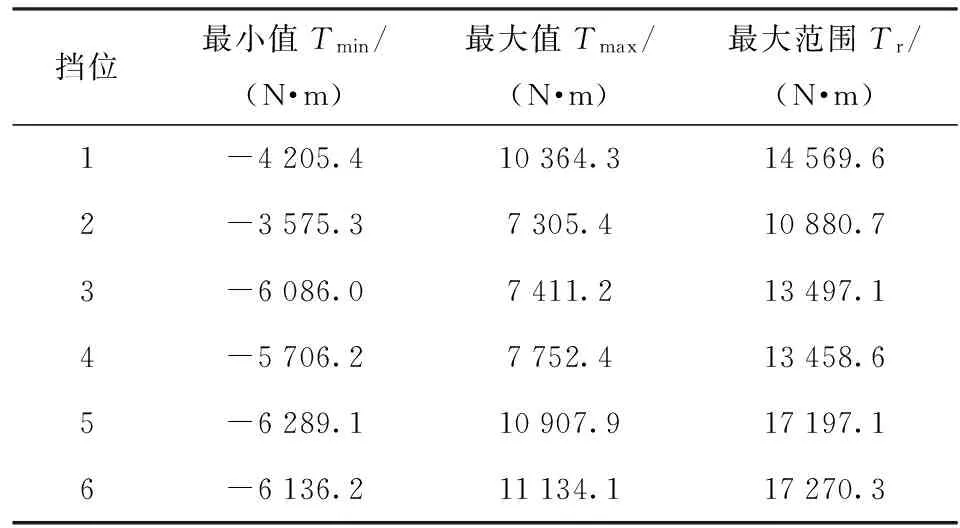
表3 扭矩数据按挡位统计
由表3的统计结果,可初步确定雨流计数的范围和组数,通过4点法雨流计数得到各挡位的雨流矩阵(RFM)。将幅值级别最小(不造成疲劳损伤)的一组载荷循环舍去,即达到去除高频噪声的目的,并可避免去除有效的载荷循环。将所有挡位的RFM合并,绘制载荷循环频次柱状图和等高线图,如图2和图3所示。

图2 试验载荷RFM柱状图Fig.2 Histogram of rain-flow matrix of test loads

图3 试验载荷RFM等高线图Fig.3 Contour map of rain flow matrix of test loads
3.2 基于核密度估计的编谱流程
由于载荷均值和幅值独特的独立分布形式(见图4),导致RFM均值和幅值二维分布呈现出不规则形状。本文采用适用于任意分布形式的二维核密度估计来拟合实测RFM.

图4 RFM的均值和幅值独立分布Fig.4 Distribution of amplitude and mean values of rain-flow matrix
在应用核密度估计过程中,需对均值和幅值二维平面划分网格,即均值和幅值分组。如果雨流计数和核密度估计的均值和幅值分组出现不一致,很容易导致估计失真。图5(a)为由5挡RFM得到的均值直方图,图5(b)为与图5(a)采用的分组不一致时的均值直方图。当重新分组与原始数据不一致时会出现图5(b)的情况。

图5 5挡RFM的均值直方图Fig.5 Mean value histogram of 5th gear RFM
为了解决应用核密度估计时遇到的上述问题,本文的编谱流程将对实测扭矩载荷采用2次雨流计数,操作步骤如下:
1) 基于实测扭矩统计结果,确定第1次雨流计数的扭矩范围;
2) 根据第1次雨流计数结果做均值和幅值极值推断;
3) 由极值推断结果确定第2次雨流计数的扭矩范围;
4) 对第2次雨流计数结果做二维核密度估计,扭矩范围、分组数与步骤3保持一致;
5) 基于二维核密度估计生成均值和幅值二维载荷谱。
为了将二维核密度估计有机结合到载荷谱的编制过程中,提出一种新的编谱流程(见图6),可以很好地拟合实测均值和幅值分布,避免核密度估计分组不一致时产生的失真效果。
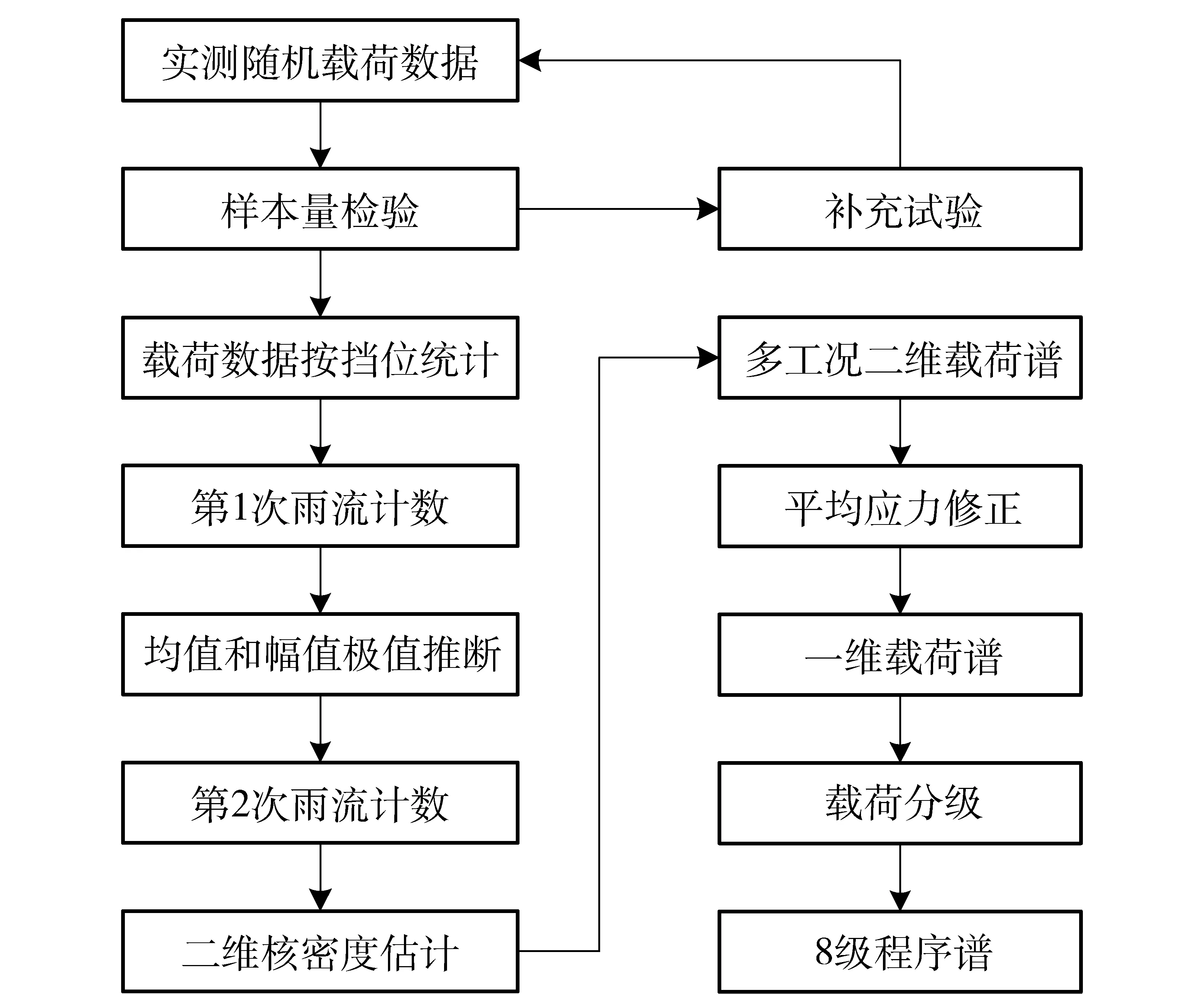
图6 载荷谱编制流程Fig.6 Load spectrum compiling procedure
3.3 均值和幅值极值推断
由第1次雨流计数的结果得到幅值和均值的独立分布,然后分别用载荷函数法拟合。采用Anderson-Darling(AD)统计量作为拟合优度,AD值越小说明分布拟合得越好。选择AD平均值较小的分布作为拟合分布,可得各挡位均值和幅值独立分布的拟合参数,结果如表4和表5所示,载荷幅值的拟合分布选择对数正态分布,均值的拟合分布选择正态分布。

表4 各挡位幅值分布拟合结果

表5 各挡位均值分布拟合结果
取建议概率值P=10-6以确定载荷极值[1],由载荷幅值的对数正态概率密度函数fX(x),可得幅值极大值的推断公式为

(4)
由(4)式可求得各挡位载荷幅值的极大值xmax. 同理,可求得各挡位均值的极大值和极小值。由各挡位均值和幅值极值的最大值计算扭矩范围,并选定分组数做第2次雨流计数。
3.4 二维核密度估计
采用基于高斯核的核密度估计来拟合第2次RFM的均值和幅值分布,二维核密度估计算法如下:
在二维平面R2上有N个独立的样本YN≡{y1,…,yN},来自于未知连续概率密度函数f,高斯核密度估计定义如下:

(5)
式中:高斯核为
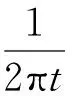
(6)
x=[x1,x2]T,y=[y1,y2]T,x和y的第1变量为幅值,第2变量为均值;t为带宽。
渐近最优平方带宽由(7)式给出:
t*=[2πN(ψ0,2+ψ2,0+2ψ1,1)]-1/3,
(7)
式中:
(8)
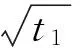
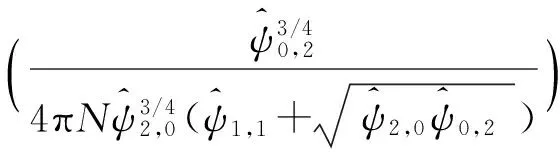
(9)
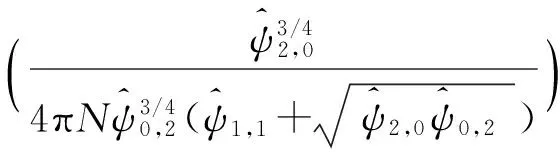
(10)
基于上述算法,可得到各挡位RFM的密度估计,操作步骤如下:
1) 以第2次雨流计数的扭矩范围和分组数划分二维核密度估计网格;
2) 使用改良Sheather-Jones方法计算第2次RFM的最优对角带宽;
3) 对第2次RFM做二维高斯核密度估计;
4) 以各挡位的均值和幅值极值范围修正密度估计,并将密度和归一化。
3.5 多工况二维载荷谱生成
做载荷频次外推时,需知道各工况载荷循环频次的发生频率[17]。假定车辆在q种工况下行驶,各工况的试验里程分别为d1,d2,…,dq,由试验统计得到的各工况载荷循环频次分别为n1,n2,…,nq,则第i个工况的载荷循环在单位里程下发生的频率为

(11)
若车辆的设计使用寿命里程为dl,各工况的行驶里程占使用寿命里程的百分比分别为p1,p2,…,pq,则第i个工况下的行驶里程为pidl,该工况出现的载荷循环频次为Ni=fipidl,于是所有工况下出现的载荷循环总频次为
(12)
设计使用寿命里程取10 000 km,计算出各工况的外推载荷频次如表6所示,则外推比例为
(13)
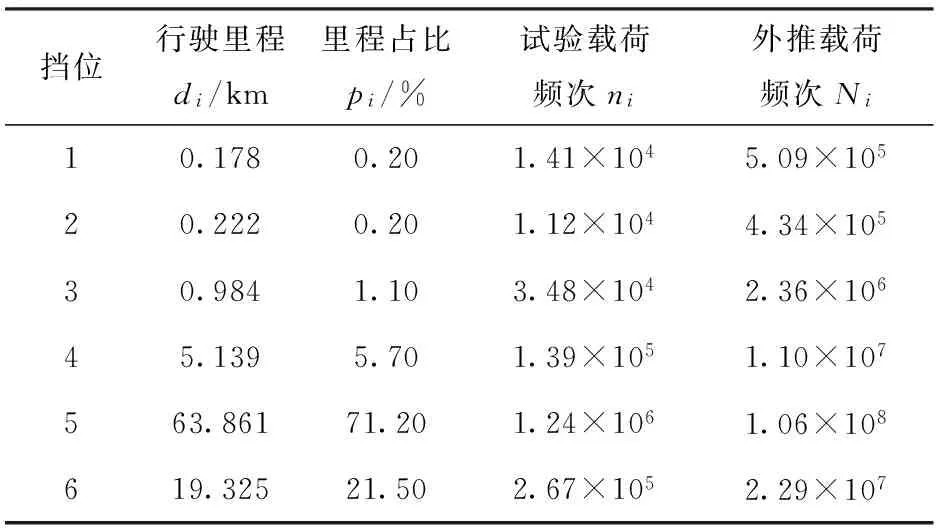
表6 各工况载荷频次外推
由上述推导,可得到多工况二维载荷谱
(14)
多工况二维载荷谱的三维柱状图和等高线图如图7和图8所示。对比实测RFM可以看出,本文所提出的基于核密度估计的载荷谱编制流程能够高度拟合实测均值和幅值二维分布。
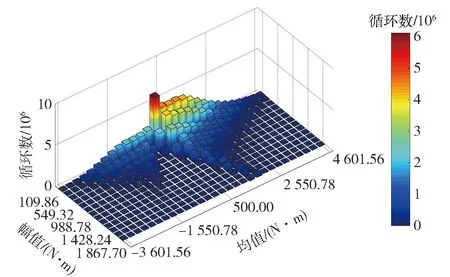
图7 多工况二维载荷谱柱状图Fig.7 Histogram of 2-D load spectrum

图8 多工况二维谱等高线图Fig.8 Contour map of 2-D load spectrum
4 8级程序谱生成与疲劳分析
4.1 8级程序谱生成
程序块谱在疲劳研究及产品设计初期,能够大大节省试验成本与缩短开发周期,应用十分广泛[18]。为获得8级程序块谱,先由二维载荷谱转换成一维载荷谱,最常用的方法是采用Goodman方程做平均应力修正。
采用不等间隔法[1]将一维载荷谱简化成8级块状载荷谱。一维载荷谱的幅值最大值为23 652.8 N·m,乘以不等间隔比例系数即可得到8级幅值水平,如表7所示。

表7 程序块谱各级幅值水平
考虑到高频次、小幅值载荷不造成疲劳损伤但会增加试验成本,故做低载舍去。本文的低载舍去阈值取第8级幅值的0.8倍。由以上方法得到一维载荷谱的对数累积频次曲线,如图9所示。图9(a)为低载舍去前,频次和为1.43×108;图9(b)为低载舍去后,频次和为9.67×105.

图9 一维载荷谱对数累积频次曲线Fig.9 Logarithmic accumulative cycles curves of spectrum
为了观察上述编谱流程对RFM的外推效果,现将实测RFM直接乘以外推倍数,然后做平均应力修正,得到的对数累积频次曲线如图10中的实线所示。从图10可以看出,本文编制出的载荷谱(虚线)与RFM有相似概率密度分布的同时,还能够对未测到的雨流循环进行外推,外推部分与实测部分相比斜率突然变大,意味着外推雨流循环出现的概率大幅较少、频次累积较慢,与实现情况相符,实现了RFM的合理外推。
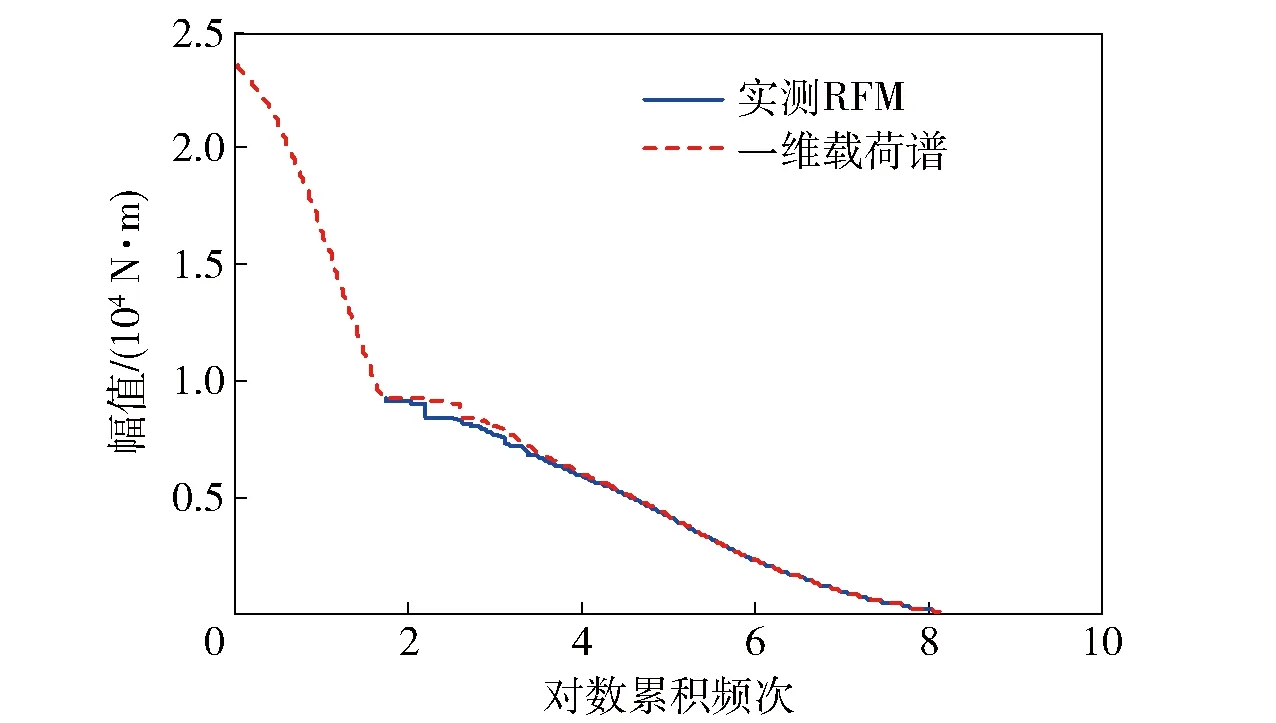
图10 RFM对数累积频次曲线Fig.10 Logarithmic accumulative cycles curve of RFM
将一维载荷谱转换为8级程序谱,采用向上等效方法,将幅值在1级与2级之间的对称载荷循环,采用等损伤方法[19]转换成幅值为1级的对称载荷循环,然后依此类推,将全范围内的对称载荷循环转换为8个幅值级别的对称载荷循环。等效损伤转换公式为
(15)
式中:ne为等效循环频次;Se为等效载荷幅值;m为应力- 寿命曲线的幂指数。8级程序块谱的对数累积频次梯形曲线如图11所示。

图11 8级程序块谱Fig.11 Eight-level program block load spectrum
为了解转速的使用规律,统计了12圈传动轴转速在扭矩维度上的分布情况,如图12蓝线所示。由图12可以观察出:当扭矩在0~3 000 N·m范围内(左数第1级红线),转速稳定在1 807 r/min附近;当扭矩在3 000~5 100 N·m范围内(第2级红线),转速波动较大,其平均值为1 617 r/min;当扭矩大于5 100 N·m时(第3级红线),转速分布越来越稀疏,其平均值为1 490 r/min. 因此,建议台架试验时由以上观察分析结果采取3级转速加载扭矩载荷。

图12 转速在扭矩维度上的分布Fig.12 Distribution of rotational speed on torque
4.2 疲劳损伤计算
本文所研究的传动轴材料为20Cr2Ni4A,材料参数由文献[1]查得,考虑影响疲劳强度的主要因素为有效应力集中系数,通过基本Miner法则计算得到一维载荷谱的疲劳损伤量,计算公式为
(16)
式中:SE为对应无限寿命NE=107的疲劳极限。
一维载荷谱的累积损伤曲线如图13所示。图13(a)为低载舍去前,损伤和为0.010 1;图13(b)为低载舍去后,损伤和为0.010 0. 对比低载舍去前后,频次和减少99.33%,损伤和减少0.29%. 由此可以看出,本文的低载舍去阈值选择合理,在保持损伤和基本不变的情况下大大减少了载荷的加载频次。
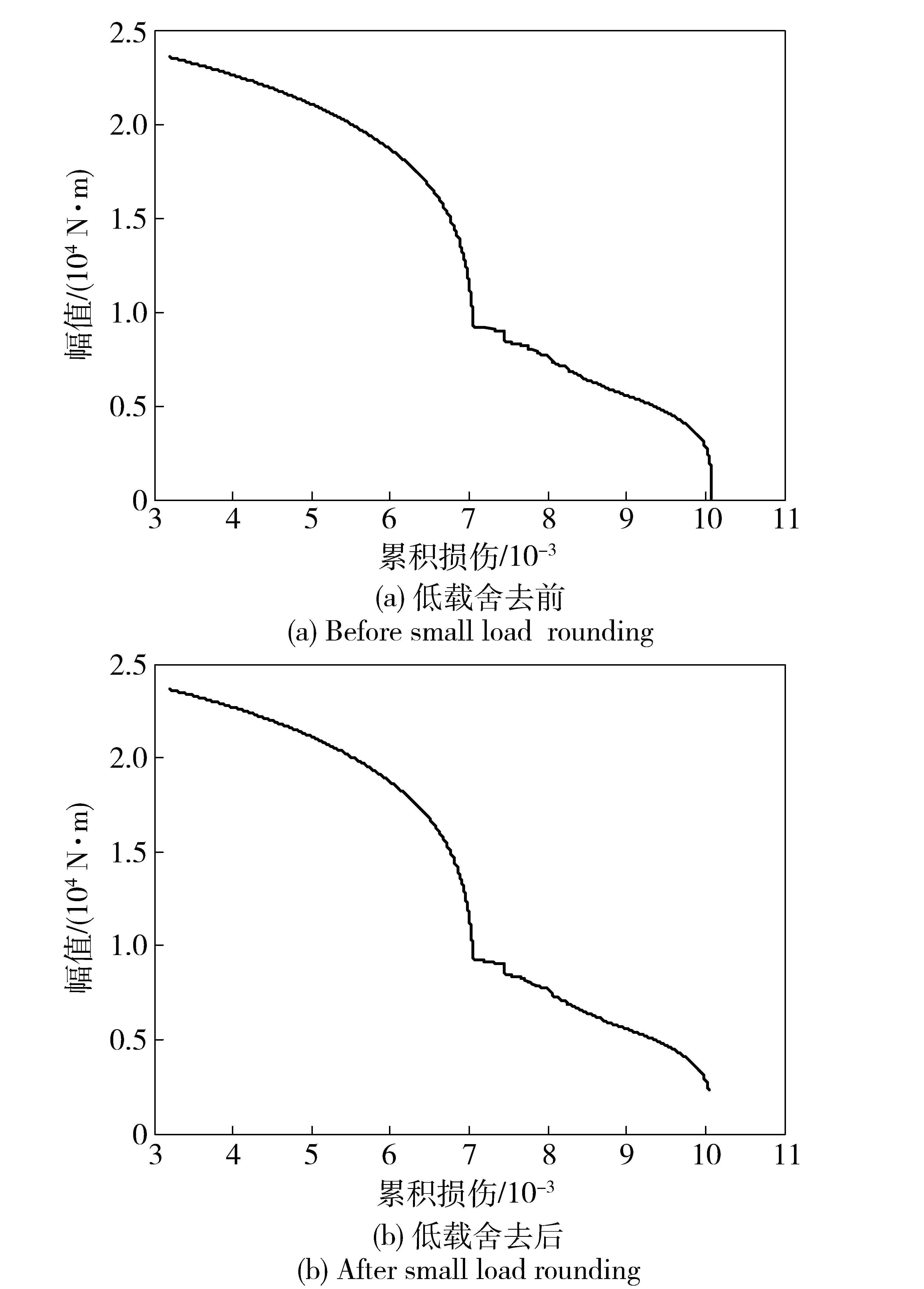
图13 累积疲劳损伤曲线Fig.13 Accumulative fatigue damage curves
5 结论
本文研究了履带车辆传动轴载荷谱的编制方法,得到以下主要结论:
1) 用最少测试次数判据对实测载荷样本数据做检验,表明本次试验数据满足80%置信度,后续可增加试验次数来提高载荷数据的置信水平。
2) 采用二维核密度估计拟合实测RFM的不规则分布,提出一种新的采取两次雨流计数的编谱流程,第1次雨流计数用于均值和幅值极值推断,第2次雨流计数用于核密度估计。从实测RFM与设计载荷谱的对比上看,本文编制出的载荷谱与实测RFM具有高度相似的概率密度分布,同时还实现了RFM的合理外推。
3) 低载舍去阈值取第8级幅值的0.8倍,使得低载舍去后,频次和减少99.33%,损伤和只减少0.29%,验证了该低载舍去阈值的合理性。此外,通过统计传动轴转速在扭矩维度上的分布,给出了3级转速加载扭矩的方法。
References)
[1] 赵少汴,王忠保. 抗疲劳设计:方法与数据[M]. 北京: 机械工业出版社,1997:81-88. ZHAO Shao-bian, WANG Zhong-bao. Anti-fatigue design: me-thods and data[M]. Beijing: China Machine Press, 1997:81-88. (in Chinese)
[2] Lee Y L. Fatigue testing and analysis: theory and practice[M]. London, UK: Butterworth-Heinemann, 2005:77-102.
[3] 阎楚良,高镇同. 飞机高置信度中值随机疲劳载荷谱的编制原理[J]. 航空学报,2000,21(2):118-123. YAN Chu-liang, GAO Zhen-tong. Compilation theory of median stochastic fatigue load spectrum with high confidence level for airplane [J]. Acta Aeronautica et Astonautica Sinica, 2000, 21(2):118-123. (in Chinese)
[4] 安东诺夫В М. 军用履带车辆传动装置[M]. 王红岩,芮强,高连华,等,译. 北京:国防工业出版社, 2014:183-208. Antonov В М. Military tracked vehicle transmission device [M]. WANG Hong-yan, RUI Qiang, GAO Lian-hua, et al, translated. Beijing: National Defense Industry Press, 2014:183-208. (in Chinese)
[5] Zuo F J, Huang H Z, Zhu S P, et al. Fatigue life prediction under variable amplitude loading using a non-linear damage accumulation model[J]. International Journal of Damage Mechanics, 2015,24(5): 767-784.
[6] Botev Z I, Grotowski J F, Kroese D P. Kernel density estimation via diffusion[J]. The Annals of Statistics, 2010, 38(5): 2916-2957.
[7] Wang J X, Liu Y, Zeng X H, et al. Selection method for kernel function in nonparametric extrapolation based on multicriteria decision-making technology[J]. Mathematical Problems in Engineering, 2013 (8) :561-576.
[8] 李莺莺, 杨清淞, 刘志东, 等. 挖掘机液压泵载荷分析及编谱方法研究[J]. 工程机械, 2015,46 (2): 14-20. LI Ying-ying, YANG Qing-song, LIU Zhi-dong, et al. A study on load analysis and compilation method of load spectrum for excavator’s hydraulic pumps[J]. Construction Machinery and Equipment, 2015,46 (2): 14-20. (in Chinese)
[9] 李研. 轮式装载机载荷谱编制中非参数外推方法研究[D].长春:吉林大学,2016:21-38. LI Yan. Research on non-parametric extrapolation method in compiling load spectra of wheel loader[D]. Changchun: Jilin University, 2016:21-38. (in Chinese)
[10] Heuler P, Klätschke H. Generation and use of standardised load spectra and load-time histories[J]. International Journal of Fatigue, 2005, 27(8): 974-990.
[11] Xiong J J, Shenoi R A. A load history generation approach for full-scale accelerated fatigue tests[J]. Engineering Fracture Mechanics, 2008, 75(10):3226-3243.
[12] 闫楚良. 飞机载荷谱实测技术与编制原理[M]. 北京: 航空工业出版社, 2010:212-239. YAN Chu-liang. Measurement technology and compilation theory of load spectrum for aircraft[M]. Beijing: Aviation Industry Press, 2010:212-239. (in Chinese)
[13] 王继新, 季景方, 胡际勇, 等. 基于贝叶斯理论的工程车辆载荷样本长度计算方法[J]. 农业工程学报, 2011, 27(6): 148-151. WANG Ji-xin, JI Jing-fang, HU Ji-yong, et al. Bayesian method for determination of load sample size in engineering vehicles [J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(6): 148-151.(in Chinese)
[14] Lee Y L, Barkey M E, Kang H T. Metal fatigue analysis handbook: practical problem-solving techniques for computer-aided engineering[M]. Oxford, UK: Butterworth-Heinemann, 2011:61-87.
[15] 郑松林, 梁国清, 王治瑞, 等. 考虑低幅锻炼载荷的某轿车摆臂载荷谱编制[J]. 机械工程学报, 2014, 50(16): 147-154. ZHENG Song-lin, LIANG Guo-qing, WANG Zhi-rui, et al. Compilation of automotive lower control arm spectrum based on the low-amplitude training load[J]. Journal of Mechanical Engineering, 2014, 50(16): 147-154.(in Chinese)
[16] Scott D W. Multivariate density estimation: theory, practice, and visualization[M]. 2nd ed. Hoboken, US: John Wiley & Sons, 2015:137-192.
[17] 项昌乐.车辆传动系轴类零件疲劳设计与变矩器动态特性研究[D].北京:北京理工大学,2001:7-26. XIANG Chang-le. The study on fatigue design of the axles and the dynamic characteristics of the torque converter in the vehicle transmission system[D]. Beijing: Beijing Institute of Technology,2001:7-26. (in Chinese)
[18] Kadhim N A, Mustafa M, Varvani-Farahani A. Fatigue life prediction of low-alloy steel samples undergoing uniaxial random block loading histories based on different energy-based damage descriptions[J]. Fatigue & Fracture of Engineering Materials & Structures, 2015, 38(1): 69-79.
[19] 张英爽. 装载机传动系载荷谱的测取与应用研究[D]. 长春: 吉林大学, 2014:20-23. ZHANG Ying-shuang. Research on the load spectra acquisition and application of loader powertrain[D]. Changchun: Jilin University, 2014:20-23. (in Chinese)
LoadSpectrumCompilingforTransmissionShaftofTrackedVehicleBasedonKernelDensityEstimation
LIU Hai-ou1, ZHANG Wen-sheng1, XU Yi2, ZHAO Zi-ye1
(1.National Key Laboratory of Vehicle Transmission, Beijing Institute of Technology, Beijing 100081, China;2.China North Vehicle Research Institute, Beijing 100072, China)
TJ810.3+22
A
1000-1093(2017)09-1830-09
10.3969/j.issn.1000-1093.2017.09.021
2017-01-11
国家国防科技工业局技术基础科研项目(3030021221505)
刘海鸥(1975—), 女, 副教授, 博士。E-mail: bit_lho@bit.edu.cn
