Fine-grained Image Categorization Based on Fisher Vector

Xiaolin Tian, Xin Ding, Licheng Jiao, and Maoguo Gong

Fine-grainedImageCategorizationBasedonFisherVector

Xiaolin Tian*, Xin Ding, Licheng Jiao, and Maoguo Gong

Fine-grained image categorization is a categorization task, where classifying objects should be the same basic-level class and have similar shape or visual appearances. In general, the bag-of-words (BoW) model is widely used for image classification. However, it has a process of damage for the feature quantization in image representation, and also severely limits the descriptive power of the image representation. Fisher vectors employ soft assignments and reduce information loss due to quantization by calculating the gradient for each parameter separately, which have been shown to outperform other global representations on most benchmark datasets. In this paper, the acquired template is represented by Fisher Vector (FV). Using the improved spatial pyramid matching (SPM) to combine FV separately, we use a method, i.e., FV+SPM, to obtain a feature representation. The experimental results show that our method is superior to the most advanced classification method in the Caltech-UCSD Birds dataset.

image categorization; fisher vector; template matching

1 Introduction

Classifying objects have a similar shape or visual appearances, and they are belonging to the same basic-level class. Fine-grained image categorization is designed to achieve this categorization task[1-3]. Fine-grained categorization needs more local information than the basic-level categorization, and the obtained feature should be more discriminative and characteristic. Fine-grained categorization will be widely used in many different applications.

Fine-grained categorization requires an algorithm to discriminate delicate differences among highly similar object classes. Traditional bag-of-words (BoW) approach does not meet the requirements of fine-grained categorization. BoW model is constructed for fine-grained categorization, which can produce more redundant words than the general image categorization. However, that will increase computation complexity. Moreover, BoW model doesn’t describe direction information. Fisher vector (FV)[4]avoids this default and can fit image data. FV is a coding method derived from the Fisher core. Standardized FV is used as a critical step in achieving good performance. A template matching approach is proposed, and it can effectively preserve image detail information. Recently, the performance of template matching has been greatly increased by FV which codes higher order statistics of local features. In this paper, fine-grained image categorization with FV based on template matching is implemented. For training samples, feature points are extracted and the distribution model of these feature points is constructed by Gaussian mixture model (GMM). Accordingly, we can obtain the FV feature by the derivation of the GMM.

The scale and orientation of object in an image need not be specifically processed, because the FV represents the entire distribution feature of image. That is to say, FV feature has the invariant attribution of scale and orientation. Due to the better discriminative and characteristic of FV feature, the proposed method performs well even with simple linear classifiers. Since template represented by FV feature lacks position information of feature points. In this paper, we introduce spatial information based on improved spatial pyramid matching (SPM)[5]. Spatial pyramid is gathered on different spatial resolution in partially disordered images. SPM achieves the statistics on different levels, and it mainly reflects the statistical feature of information distribution.

The remaining part of this paper is organized as follows: Section 2 discusses related work. Section 3 describes the FV and GMM. Section 4 describes templates and feature representation. Section 5 describes image coding based on SPM. Experiment results are described in Section 6, and Section 7 concludes this paper.

2 Related Work

Image categorization has been studied for many years. Perhaps BoW model is the most common method for describing local features in an image[6]. Recently, the BoW model has been greatly enhanced by FV[7]. However, the BoW model discards the spatial order of local descriptors. A codebook-free and annotation-free approach is proposed for fine-grained image categorization in [8]. SPM for modeling the spatial layout of the local features has been developed.

In this paper, we achieve fine-grained image categorization with FV based on template matching. For training samples, feature points are extracted and these feature points are modeled based on Gaussian mixture model (GMM). And then, the FV feature by derivation of the GMM can be obtained. We introduce image coding based on improved SPM. Spatial pyramid is gathered on different spatial resolution in partially disordered images. Due to statistics on different levels, SPM model is able to influence on statistical feature of information distribution.

3 The FV and GMM

In this section, we introduce the Fisher Vector (FV) and establishment of GMM. We first describe the principle of the Fisher kernel (FK)[9], and then describe the GMM model.

3.1 The Fisher Kernel

In this section, we introduce the Fisher Vector (FV) and GMM model. We first describe the principle of the Fisher Kernel (FK)[9]. LetX={xt,t=1,2,…,T} be a sample set of local feature descriptors,Tis the number of the samples.Xcan be described as the following gradient vector[9]:

(1)

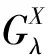
(2)

Fλ=Ex～u λ[▽λloguλ(x)▽λloguλ(x)′]

(3)

Assuming that the above feature distribution is independent and governed by the mixture Gaussian distribution, we can useKGaussian distributions to express these independent distributions. Let the parameterλ={wi,μi,∑i,i=1,2,…,K}, we can obtain the value of logarithm:

(4)

(5)

(6)

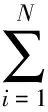
(7)

(8)

(9)

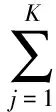
3.2 FV normalization

We now describe two normalization steps after the FV is obtained[10-11].

L2-normalization. When two images contain the same object and have different amount of background information (e.g. the same object at different scales), we will obtain different signatures. Especially, small objects with a small specific information value will be difficult to be detected. To remove the dependence on specific information, we can use L2-normalization[12]to replace Kernel:

(10)

PowerNormalization. The great number of similar Gaussian function is yielded with the increase of the number of Gaussian, which results in redundant FV feature. We intend to use the following function to achieve power normalization in each dimension:

(11)

where 0≤α≤1 is a normalized parameter, and the parameter value will change with the number of Gaussian. In practice, combining L2-normalization with power normalization, we firstly execute power normalization, and then use L2-normalization, which can eliminate the influence of two types of normalization. The categorization performance will be better than non-normalization.

4 Templates and Feature Representation

Fig.1 Acquisition of the templates.

5 Image Coding based on SPM

SPM procedure divides an image into three different levels, i.e., layer 0, layer 1, and layer 2, and then we can deal with statistical image information for each level. The process is shown in Fig.2. The first layer is divided 4 blocks, the second layer is divided 16, and the layeriis divided blocks 2i×2i. The final image is consist of concatenated and normalized statistical information at different levels in different blocks.

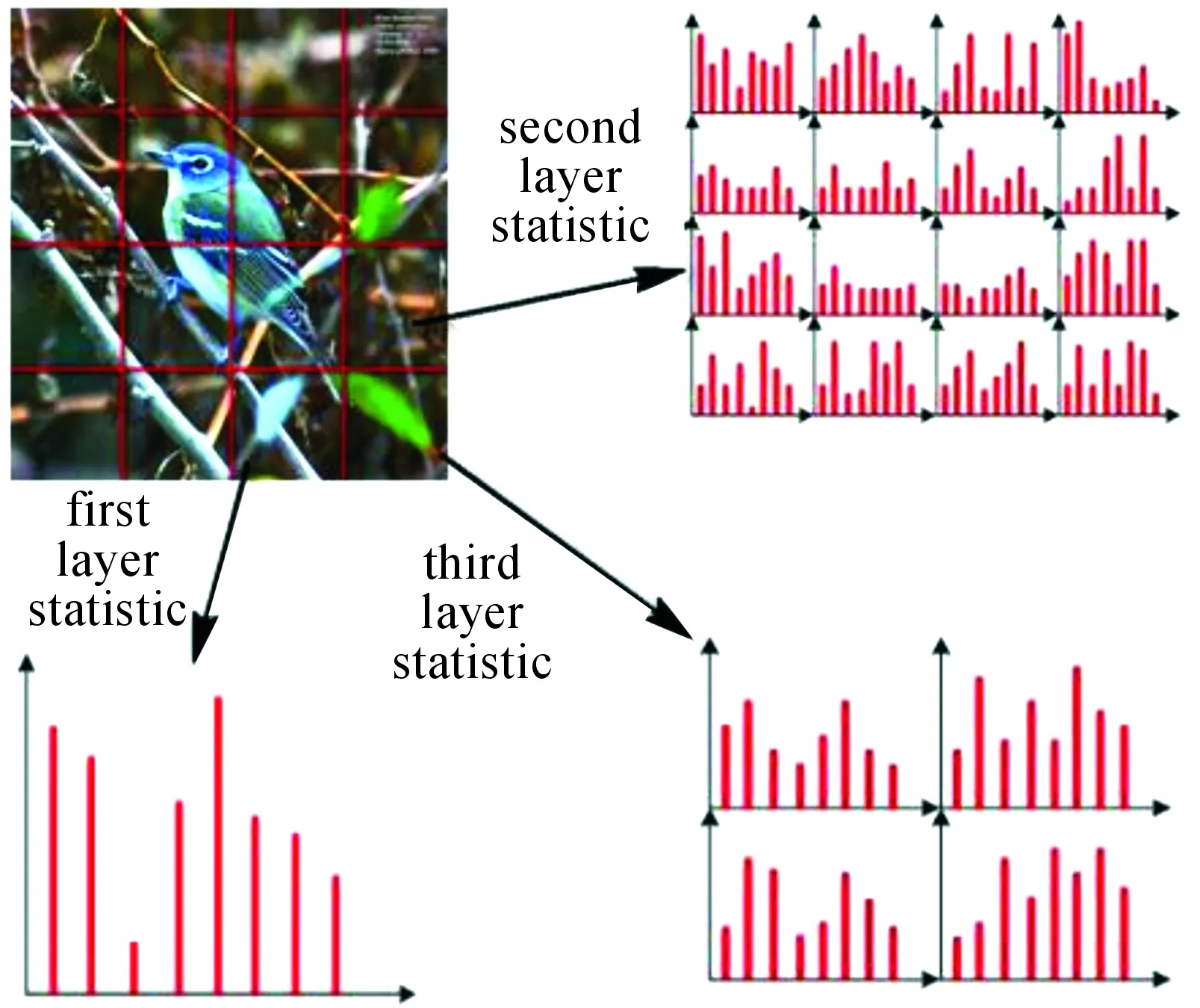
Fig.2 Construction of SPM

Generally, two layers of Pyramid are used to deal with statistical information, which is beneficial for reducing computational complexity[20]. From each block, the three biggest similarity of response diagram is taken at the layer 0. The layer 1 and layer 2 are the same processing step in each block. The three locations with biggest similarity values should have a certain distance, which is beneficial for whole statistics of a block. After obtaining statistical distribution of whole and local similarity, we are able to represent response vector of a template on the image[21]. So that response vectors of all the templates are jointed. Finally, the statistic feature of each image is obtained by matching the same template sets.

Based on above description, the step of proposed algorithm is described as follows:

1) Extract features;

2) Establish GMM based on all the feature points;

3) Obtain templates in the specified training samples;

4) All of the templates are represented by FV;

5) Code feature representation based on SPM;

6) Match each template and image and obtain response diagram of similarity;

7) The spatial hierarchical statistics representation is jointed as image coding;

8) Carry out image categorization using SVM;

9) According to confusion matrix, output the categorization accuracy.

6 Experiments

The proposed method is implemented in MATLAB (Version R2010a) on a machine with an Intel core i5-5200 CPU, 8 GB memory and Microsoft Windows 7 operating system.

Caltech-UCSD Birds dataset (CUB-200)[22]is widely used in the fine-grained image categorization. It contains 15 training images and 10 to 25 test images for each category, which is in total of 200 bird images. For verifying our categorization performance, a part of the image library are used from the Black Capped Vireo to the Downy Woodpecker[23], which contains 13 categories of birds.

CUB-200 dataset has handled a coarse segmentation well, which can be used in our training samples. Take out the target from images as a new training sample set, and get a template in the selected target image. We select templates with five sizes, i.e.,WH=[20 20; 50 50; 100 100; 50 80; 80 50 ], whereWHis width and height of a template in the experiment.

Since images have been segmented roughly in this dataset, we use a method called super-pixel segmentation(SLIC) to deal with the segmented target regions of images in the training samples. The number of super-pixel blocks is initialized 150 blocks, and RGB features of each image are extracted. Using these RGB feature points to establish GMM. Fig.3 shows that the number of GMM affects algorithm performance.

In experiments, we firstly determine how many GMM is the best to implement classification. We randomly select six different locations in each training samples, so that we get 13×15×5×6=5850 templates, which is expressed by FV coding with power normalization and L2-normalization. Finally, we use 1×13 vectors in SPM model that represents the matching result of each template. When the number of GMM is larger and the number of feature point is fewer, the average accuracy rate will decline; when the number of GMM is fewer, it is more difficult to obtain the accurate feature distribution. As a result, five GMM are selected in our experiments.

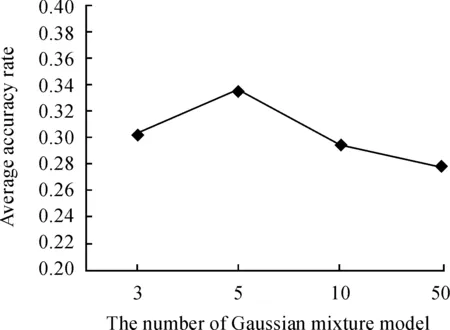
Fig.3TherelationbetweenalgorithmperformanceandnumberofGMM.

Fig.4(a) shows response diagram of a template in an image, where we consider the three maximum similarity values with a certain distance. The distance among the three points with maximum similarity values should larger than 0.1 times the width (height). In Fig.4(b), the image is divided into 2×2 blocks, and we only consider the maximum similarity value of each block; In Fig.4(c), the image is divided into top, middle and bottom part. We only consider the maximum similarity value of each block. The processing procedure of Fig.4(d) is similar to Fig.4(c). Finally, we can get a vector with thirteen dimensions, which represent the coding of a template in an image. In experiments, we extract only the RGB feature and use coding method based on the SPM model. The number of templates, randomly selected from each training image, has great influence on image coding. Fig.5 shows how the number of templates affects algorithm performance.

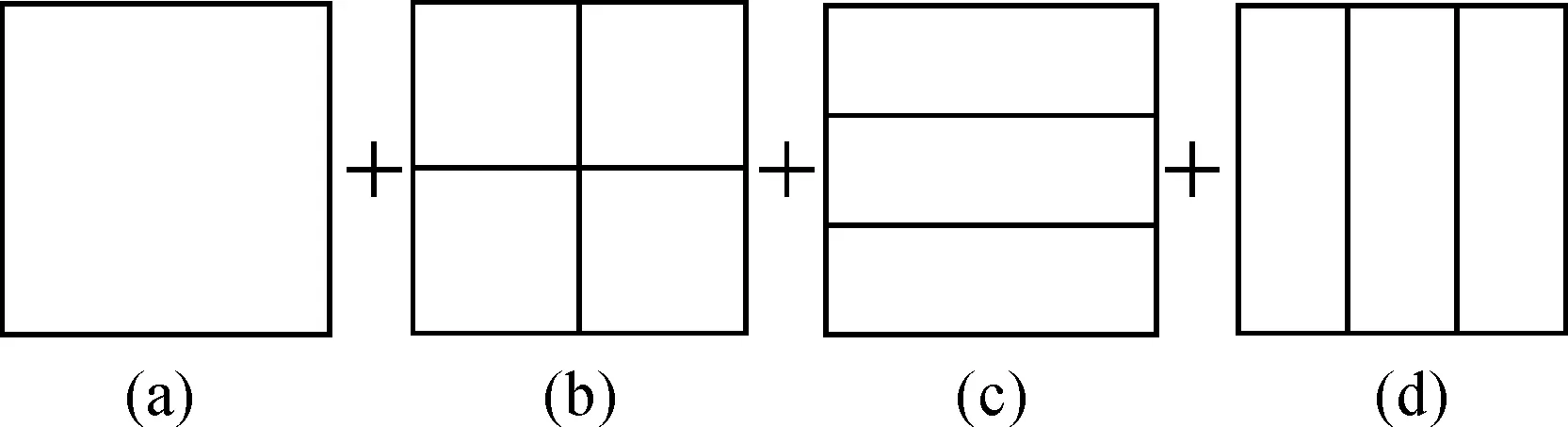
Fig.4 Formation of 1×13 vector

We selected 50 templates from each training image in our experiments. CUB-200 dataset has 13 categories, and each category has 15 training images, from which we select 10 images. And then, we get 13×50×10=6500 templates. Each template corresponds to a 1×13-dimensional image representation. The final dimension of an image is 6500×13=84500. We reduce the dimension of the image representation by principal component analyses (PCA), and implement classification with support vector machine (SVM).

In experiments, it takes 2 minutes 10 seconds for extracting features and FV representation based on SPM needs 44 minutes 20 seconds. It is in total of 46 minutes 30 seconds. For accurately describing image information, FV representation based on SPM is implemented by two traverses in our experiments, which takes most of the time. In addition, we achieve two other models: FV+VQ (Vector Quantization) and FV+LLC (locality-constrained linear coding). The compared methods include: cSIFT+SPM[24], MKL[25], Birdlet[26], and CF+AF[19]. Confusion matrix and mean average precision (MAP) is used as evaluation criteria, and the classification results are shown in Table 1. Compared with other methods from Table 1, we know that our method improves classification performance.

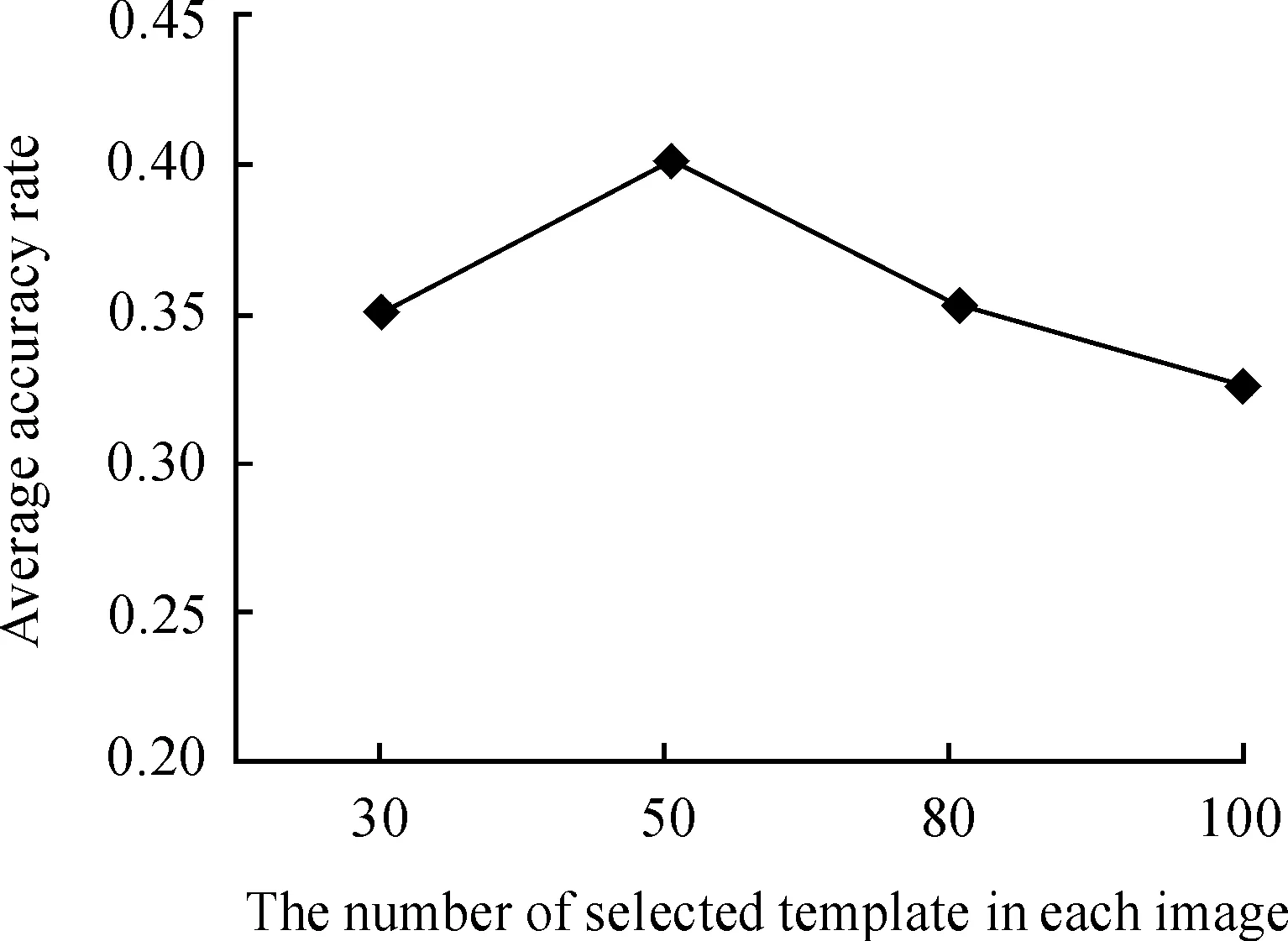
Fig.5Therelationbetweennumberoftemplateandalgorithmperformance.

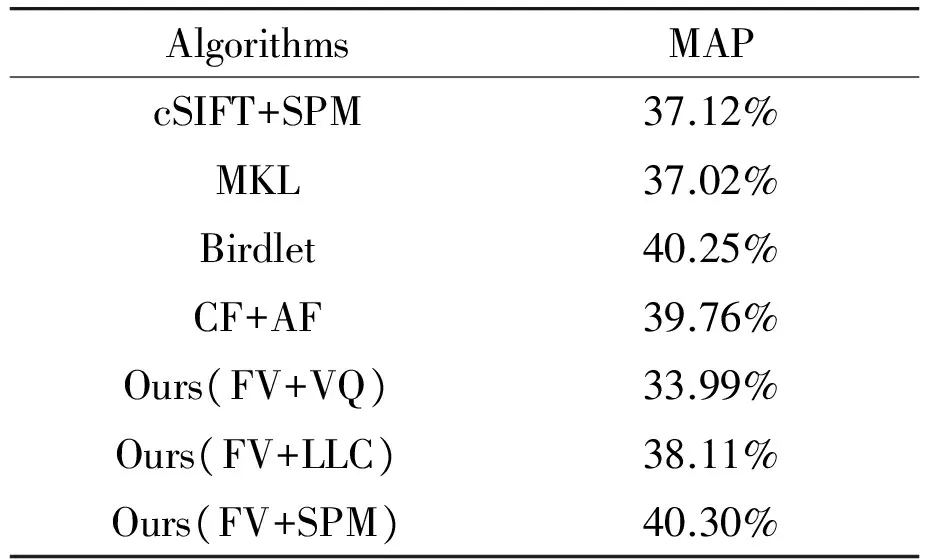
Table 1 Comparison of classification results.

7 Conclusion

In this paper, we use a FV coding method to implement fine-grained image categorization. After extracting feature points and creating GMM model, the statistic feature of FV coding of each image is obtained. Furthermore, FV coding of an image based on SPM is achieved, and the spatial hierarchical statistics is obtained for coding image. Finally, SVM classifier is carried out to finish the image categorization. Generally, our method improves the accuracy rate of fine-grained image categorization compared with other methods.

Acknowledgment

This work was supported by the National Natural Science Foundation of China under Grant 61571342, 61573267, 61473215; by the National Basic Research Program of China under Grant 2013CB329402; by Natural Science Basic Research Plan in Shaanxi Province of China under Grant 2017JM6032.

[1]I. Biederman, S. Subramaniam, M. Bar, P. Kalocsai, and J. Fiser, Subordinate-level object classification reexamined,Psychol.Res., 62(2-3): 131-153, 1999.

[2]S.Branson, C.Wah, F.Schroff, B.Babenko, P.Welinder, P.Perona, and S.Belongie. Visual recognition with humans in the loop, inProceedingsofEuropeanConferenceonComputerVision, Crete, Greece, 2010, pp.438- 451.

[3]A. Hillel and D. Weinshall,Subordinate class recognition using relational object models, inNeuralInformationProcessingSystems2006(NIPS),Canada,2006,pp.73-80.

[4]J. Yang, K. Yu, Y. Gong, and T Huang, Linear spatial pyramid matching using sparse coding for image classification, inProceedingsof2009IEEEConferenceonComputerVisionandPatternRecognition(CVPR), Miami, USA,2009, pp.1794-1801.

[5]S. Lazebnik, C. Schmid, and J. Ponce,Beyond bags of features: spatial pyramid matching for recognizing natural scene categories, inProceedingsof2006IEEEConferenceonComputerVision and Pattern Recognition (CVPR), New York, USA, 2006, pp.2169-2178.

[6]J. Sivic and A. Zisserman,Video google: a text retrieval approach to object matching in videos, inProceedingsof2003IEEEConferenceonComputerVisionandPatternRecognition(CVPR), Madison, USA, 2003, pp.1470-1478.

[7]W. Zheng, S. Gong, and T. Xiang, Associating groups of people, inProceedingsofBritishMachineVisionConference(BMVC), London, 2009, 23.1-23.11

[8]B. B. Yao, G. Bradski and F. F. Li, A codebook-free and annotation-free approach for fine-grained image categorization, inProceedingsof2012IEEEConferenceonComputerVisionandPatternRecognition(CVPR), Rhode Island, USA, 2012, pp.3466-3473.

[9]J. Sanchez, F. Perronnin, and T. Mensink, Image classification with the Fisher Vector: theory and practice,Int.J.Comput.Vis., vol.105,no.3,pp.222-245, 2013.

[10] F. Perronnin, J. Sanchez, and T. Mensink, Improving the Fisher kernel for large-scale image classification, inProceedingsof11thEuropeanConferenceonComputerVision(ECCV), Heraklion, Greece,2010, pp.119-133.

[11] F. Perronnin and C. Dance, Fisher kernels on visual vocabularies for image categorization, inProceedingsof2007IEEEConferenceonComputerVisionandPatternRecognition(CVPR), Minnesota, USA,2007, pp.1-8.

[12] J. Zhang, M. Marszalek, S. Lazebnik, and C. Schmid, Local features and kernels for classification of texture and object categories: a comprehensive study,Int.J.Comput.Vis., vol.73,no.2,pp.213-238,2005.

[13] H. Liu and Z. Su, Template-based multiple codebooks generation for fine-grained shopping classification and retrieval, inProceedingsofinternationalconferenceondigitalhome(ICDH), Guangzhou,China,2014, pp.293-298.

[14] S.Branson, C.Wah, F.Schroff, B.Babenko, and S.Belongie, Visual recognition with humans in the loop, inProceedingsofEuropeanConferenceonComputerVision, Crete, Greece, 2010, pp.438- 451.

[15] D. G. Lowe,Distinctive image features from scale-invariant keypoints,Int.J.Comput.Vis., vol.60,no.2,pp.91-110, 2004.

[16] K. VandeSande, T. Gevers, and C. Snoek, Evaluating color descriptors for object and scene recognition,IEEETrans.PatternAnal.Mach.Intell.,vol. 32,no.9,pp.1582-1596, 2010.

[17] P. S. Hiremath and J. Pujari,Content based image retrieval using color, texture and shape features, inProceedingsof15thInternationalConferenceonAdvancedComputing&Communication(ADCOM), Guwahati,India,2007, pp.780-784.

[18] J. Yu, Z. Qin, T. Wan, and X .Zhang, Feature integration analysis of bag-of-features model for image retrieval,Neurocomputing,vol.120, pp.355-364, 2013.

[19] Li L J, Su H, Xing E, Li.F F, Object bank: A high-level image representation for scene classification and semantic feature sparsification, inNeuralInformationProcessingSystems(NIPS), Whistler, Canada, 2010, pp.719-729.

[20] S. Maji, L. Bourdev, and J. Malik, Action recognition from a distributed representation of pose and appearance, inProceedingsof2011IEEEConferenceonComputerVisionandPatternRecognition(CVPR), Colorado Springs,USA, 2011, pp.3177-3184.

[21] A. Coates and H. Lee, An analysis of single-layer networks in unsupervised feature learning, inProceedingsofinternationalconferenceonArtificialIntelligenceandStatistics(AISTATS), FL, USA, 2011,pp. 215-233.

[22] P.Welinder, S.Branson, T.Mita, C.Wah, F.Schroff, S.Belongie, and P.Perona, Caltech-UCSD Birds 200,California Institute of Technology,CNS-TR-2010-001,2010.

[23] R. Farrell, O. Oza, N. Zhang, and VI Morariu，Birdlets: Subordinate categorization using volumetric primitives and pose-normalized appearance，inProceedingsofIEEEInternationalConferenceonComputerVision(ICCV), Barcelona,Spain,2011，pp.809-818.

[24] S. Lazebnik, C.Schmid, and J. Ponce, Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories, inProceedingsof2006IEEEComputerSocietyConferenceonComputerVisionandPatternRecognition(CVPR2006), NY, USA,2006,pp. 2169-2178.

[25] S. Branson, C.Wah, F.Schroff, B.Babenko, P.Welinder, P.Perona, and S.Belongie.Visual recognition with humans in the loop, inProceedingsof11thEuropeanConferenceonComputerVision(ECCV), Crete, Greece,2010, pp.438- 451.

[26] B. B. Yao, A. Khosla, and F. F. Li,Combining randomization and discrimination for fine-grained image categorization, inProceedingsofIEEEConferenceonComputerVisionandPatternRecognition(CVPR), Colorado Springs,USA, 2011, pp.1577-1584.

XiaolinTianis currently an Associate Professor in the Electronic Engineering School, Xidian University, Xi’an, China. He received PhD degree from Xidian University in 2008. During 2011 and 2012, he was a visiting scholar at Vision Lab, University of California, Los Angeles, USA. His current research interests are in the areas of image and video processing.

LichengJiaoreceived the B.S. degree from Shanghai Jiaotong University, Shanghai, China, in 1982, the M.S. and PhD degrees from Xi’an Jiaotong University, Xi’an, China, in 1984 and 1990, respectively.Since 1992, he has been a Professor with the School of Electronic Engineering, Xidian University, Xi’an, China. He was in charge of about 40 important scientific research projects, and published more than 20 monographs and 100 papers in international journals and conferences. His research interests include image processing, natural computation, machine learning, and intelligent information processing.MaoguoGongreceived the B. Eng degree and Ph.D. degree from Xidian University. Since 2006, he has been a teacher of Xidian University. He was promoted to associate professor and full professor in 2008 and 2010, respectively, both with exceptive admission.Gong’s research interests are broadly in the area of computational intelligence, with applications to optimization, learning, data mining and image understanding. He has published over one hundred papers in journals and conferences, and holds over twenty granted patents as the first inventor. He is leading or has completed over ten projects as the PI, funded by the National Natural Science Foundation of China, the National High Technology Research and Development Program (863 Program) of China and others. He was the recipient of the prestigious National Program for Support of Top-notch Young Professionals (selected by the Central Organization Department of China), the Excellent Young Scientist Foundation (selected by the National Natural Science Foundation of China), the New Century Excellent Talent in University (selected by the Ministry of Education of China), the Young Teacher Award by the Fok Ying Tung Education Foundation, and the National Natural Science Award of China.

2016-12-20; accepted:2017-1-20

the B.S. degree in electronic engineering from the Zhengzhou University, Zhengzhou, China, in 2015. He is currently pursuing the M. S. degree in Xidian University, Xi’an, China.

•Xiaolin Tian, Xin Ding, Licheng Jiao and Maoguo Gong are with Key Laboratory of Intelligent Perception and Image Understanding of Ministry of Education, International Research Center of Intelligent Perception and Computation, International Collaboration Joint Lab in Intelligent Perception and Computation, Xidian University, Xi’an 710071, China.E-mail:xltian@mail.xidian.edu.cn

*To whom correspondence should be addressed. Manuscript