Automated Test Data Generation Based on Particle Swarm Optimization with Convergence Speed Controller

Fangqing Liu, Han Huang, Xueqiang Li, and Zhifeng Hao

AutomatedTestDataGenerationBasedonParticleSwarmOptimizationwithConvergenceSpeedController

Fangqing Liu, Han Huang*, Xueqiang Li, and Zhifeng Hao

Automated test data generation for path coverage (ATDG-PC) plays an important role in software testing. In this paper, ATDG-PC is applied to the case of cloud computing such as Hadoop programs which are more difficult to search for high-rate path coverage than the normal programs. ATDG-PC can be modelled as an optimization problem of search. It’s a challenge because its search scale is usually enormous, while the relationship between the variables and the paths is unknown. First, a rapid meta-heuristic algorithm particle swarm optimization (PSO) was chosen to solve the problem of large-scale search. Second, the strategy of convergence speed controller was used to improve the performance of PSO by mining heuristic information from the found paths. The controller adjusts the convergence speed balance periodically by two conditions and rules. The first strategy slows the convergence speed when the algorithm is premature convergence and is trapped in a local optimum. The second strategy accelerates the convergence speed if the algorithm does not converge after many iterations. The improved particle swarm optimization with convergence speed controller is designed to generate test cases which cover the uncovered paths, while the effectiveness of the proposed algorithm is evaluated by classic Hadoop programs of cloud computing. The experimental results indicate that the proposed algorithm can reduce a great number of test cases for path coverage, compared with other meta-heuristic algorithms for automated test data generation.

automated test data generation; hadoop program; particle swarm optimization; convergence speed controller

1 Introduction

The software of cloud computing is required to be highly correct and stable because of its large number of users. Testing is crucial to its functionality. In recent years, software of cloud computing has been incorporated with an exploding number of systems. However, the complexity of software is exploding and the testing work becomes more and more difficult. Test data generation is to generate a set of test data for testing the adequacy of new or revised software application. In order to acquire high-quality software, exhaustive testing is needed. However, bugs exist in each software while we have finite resources in the lifecycle of software development[1].

In the course of software development, more than 50% of consumption was spent on the process of testing[1]. Software testing is a kind of labor-intensive work which costs a lot in software development cycle. This process accounts for more than half of the total overhead. If the process of software testing can be automated, the human resource will be saved. The cost of software development can be greatly reduced at the same time. Automated test data generation technique will help to find more bugs under the condition of finite cost[2].

The software testing methods can be divided into black-box testing and white-box testing.Black-box testing is also called the functional testing, which means that the whole logic of the software system is not exactly known, and we only need to examine whether each function has been achieved properly. On the other hand, the white-box testing, also named structural testing, is based on the fact that the test engineer knows the details about the software program. Compared with functional testing, the structural testing is considered to be more effective. This testing method has been widely applied and studied in the field of software test. Under structural software testing, Joseph R. Horgan[3]demonstrated that the coverage is effective and acceptable.

There are two types of methods for software testing data generation. One is a static method, and the other is a dynamic method. The static method does not execute the testing problem. On the contrary, it uses the method of symbolic execution to generate test data under certain coverage criterion. There are many limitations when using symbolic execution. For example, this method is not suitable for analyzing complex software program. Miller and Spooner[4]firstly proposed using the dynamic method to generate test data in software testing. At the same time, the dynamic technique generates test data which can be modelled as an optimization problem[5]. Actually, most of the software testing techniques are dynamic.

In the process of testing by the dynamic method, two kinds of evaluation criteria were proposed. The first criterion was evaluating based on the branch distance between the position and target, the second criterion was evaluating based on the similarity. The criterion based on evaluating the branch distance was firstly proposed by Nigel Tracey[6]. The fitness of input data was evaluated by comparing the difference between the actual value and the target coverage in each judgement branch. Many evolutionary computation algorithms[1, 7, 8]got the optimum solution by optimizing branch distances. The other criterion was based on evaluating the problem control flow graph. The algorithms can compare the similarity between the path generated by input data and the target path. In this way, the similarity was optimized by the evolutionary algorithms. For example, Yao[9]used GA to generate test data based on the path coverage using similarity criterion. Cao et al.[10]applied the similarity criterion to the fitness function.

The problem of automated test data generation for path coverage (ATDG-PC) can be commonly modelled as a complex optimization problem. The problem cannot be solved by the simplest strategy like random search or hill climbing[11]when its domain of input is large. Meta-heuristic algorithm with automated test data generation transforms software testing research to the optimization problems[12].

There are two categories of meta-heuristic algorithms for the ATDG-PC introduced as follows.

The first one is genetic algorithm (GA). Lin[13]proposed a GA with a fitness function based on Hamming distance to generate the case to cover the required paths. Wang[14]and Suresh[15]also took GA as the solution tools for ATCG-PC. Zhang[16]introduced the concept of multi-population to improve GA for ATCG-PC. Bouchachia[7]proposed an immune strategy to strengthen the global search capacity of GA. GA has a capacity of stochastic global search, but its computational complexity is high. As a result, it would take many test cases to complete the assignment of covering paths. The GAs commonly converges slowly, and their operators are not specifically designed to mine the heuristic information for solution. Therefore, hybrid swarm intelligence algorithms were proposed as faster meta-heuristic algorithms for improvement.

The second category is hybrid swarm intelligence algorithm. Ding[17]divided the population of GA into several swarms which were impacted by particle swarm optimization (PSO) to increase the diversity of the population. Similarly, Girgis[18]composited GA and PSO to solve ATCG-PC. Srivastava[19]proposed a meta-heuristic algorithm of GA and ant colony optimization (ACO) to increase the discovering rate of the uncovered paths. Mala[20]indicated that artificial bee colony algorithm overcomes ACO for ATCG-PC. The afore-mentioned hybrid swarm intelligence algorithms only use fitness function to evaluate the quality of the found path but do not lead the algorithm search in the next generation.

In this paper, we applied the particle swarm optimization[21]with convergence speed controller (CSC) to solve ATCG-PC problem. Particle swarm optimization converges fast, but it may prematurely converge and be trapped in local optimum. The idea of convergence speed controller is aimed to solve this problem. There are two adaptive adjusting approaches: the first one is slowing down the convergence speed when the particle prematurely converges, and the second one is accelerating the convergence speed of PSO when the particle cannot update its best solution in a preset time. After applying the CSC operator into PSO, the algorithm performs much better for test data generation problem.

This paper is structured as follows. The model of ATCG-PC and its evaluation function are outlined in Section 2. Section 3 introduces the particle swarm optimization based on convergence speed controller for ATCG-PC. Comparing result of the experiments for ATCG-PC problem are presented in Section 4 before concluding this paper in Section 5.

2 Automated Test Data Generation for Path Coverage

In this section, the problem description of automated test data generation for path coverage and evaluation function for the solution to ATDG-PC will be introduced.

2.1 Problem formulation

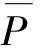
2.2 Evaluation function

In order to evaluate the generated test data, an evaluation function to show the distinction between the current position and the target position is needed. The purpose of our algorithm is to achieve 100% path coverage. The purpose of ATDG-PC is to find out at least one test case that covers each path. One of the most effective approaches is to use the heuristic information from the generated test data and the covered paths to find the uncovered paths. The proposed evaluation function is designed to be adaptively updating the message according to the covered paths. The equation of evaluation function is presented by Expression (1):

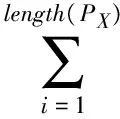
(1)

wherelenght(PX) is the number of vertexes alongPX, andf(PX,i) is the branch evaluation value of test caseXini-th vertex. We pay attention to the uncovered breach in thei-th judgement vertex ofPX, andf(PX,i) is calculated by Expression(2):

(2)

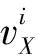
When we deal with the character string instead of number as the test data, we cannot straightly use the criterion listed in Table 1. However, each string can be identified as a list of integer number whose value is in the range of [0,127]. Once the input domain of string is changed to integer number, the criterion of Table 1 can be used to calculate the cost value of each vertex about the judgement branch of character string.

Table 1 Criterion of cost value.

*Kis a constant value.

*aandbare variables that appear in the branch node of the tested problem. They may be a known value or a complex value calculated by the preceding part of the program.

2.3 Encoding of problem input

In this subsection, we will discuss the encoding method of ATDG-PC and the challenges among the testing Hadoop programs. Considering the precision of the problems and the cost of the algorithm, we unified the input domain of the numerical problem into integers. Some real number values may be produced in the process of generating the new individuals. We will use thekintegers to present a string whilekis the length of the string. For this kind of testing problems, we assume that this set of input string is (s1,s2, …,sk), whilekis the input dimension. In order to simplify the complexity of the problem, we set the length of each character to be a constant. The length of all strings are fixed with value m. We used the ASCII code to encode each individual character. A string of lengthmin this case can be regarded as an array ofmdimensions. All arrays’ input domains are in the range of [0, 127]. Consequently, the search space of our test problem is [0, 127]k*m, which is really a large searching area. The large search space provides a challenge for the meta-heuristic algorithms.

3 Particle Swarm Optimization Based on Convergence Speed Controller

A great number of researchers applied PSO for optimization problem since PSO was simple to be programmed and converged fast. Four categories of PSOs can be classified: changing velocity strategies[22], hybrid searching operator with PSO[23], controlling the parameters[24]and using multi swarm[25].

There are two kinds of convergence speed operators discussed in this paper.The operator of the speed of swarm convergence[26]reflects the swarm diversity. The operator of global attractor convergence[27]presents the speed of particle toward optimality. Therefore, the proposed CSC designed two conditions and two rules to adjust the convergence speed.

3.1 Process of PSO-CSC

PSO is a kind of robust meta-heuristic algorithm. The particles in the algorithm are updated by the information provided from the best particle in the population, current particle’s historical best position and the old position of the current particle. Kennedy and Eberhart[28]first proposed this algorithm in 1995. Each particle in the population is on behalf of a test case. It means that the position of the particle is a test case of the test data set. The position of the particleis updated to generate new test cases as their new positions. When a new path is covered, it means that the position of the particle is right because the test case covers the target path.

Algorithm1：PSO⁃CSCfortestdatagenerationproblem Input：atestproblemϕ Output：atestsuiteXcoverstheproblem1 //Step1：Initialization2 Initializetheentireswarmofparticles’positionandvelocity，t=0，D=0andgBest=X1，recordeachpathofϕtobeuncovered3 foreachparticlei∈{1，2，…，K}do45678 gBest=Xi； iff(pBesti)>f(gBesti)then gBest=pBesti end AddXitoXifauncoveredpathiscoveredbyXi9 end10 //EndofStep111 whileterminationcriterionisnotmetdo121314151617181920212223242526272829303132333435 363738394041 t=t+1 //Step2：ParticleUpdating foreachparticlei∈{1，2，…，K}do foreachdimensionj∈{1，2，…，n}do vji=χ∗vji+c1∗r1∗(pBestji-xji)+c2∗r2∗(gBestj-xji) xji=xji+vji end iff(Xi)>f(pBesti)then pBesti=Xi end iff(pBesti)>f(gBest)then pBesti=pBesti end AddXitoXifauncoveredpathiscoveredbyXi end //EndofStep2 //Step3：convergencespeedcontroller iftmodτ=0then D=D+τ ifconditionIismetthen | RunRuleItoslowdownthespeedofswarmconvergence； end ifconditionIIismetthen | RunRuleIItoslowdownthespeedofswarmconvergence； D=0 end end foreachparticlei∈{1，2，…，K}do AddXitoXifauncoveredpathiscoveredbyXi end //EndofStep342 end43 ∗Theterminalcriterionofthisalgorithmisalltheindependentpathofϕiscoveredorthetestcasenumberexceedpresetvalue108

We will discuss the encoding about the PSO. The particles in the population represent the input value of automated software testing. Each particle in population contains two attributes, i.e., position and velocity. The position attribute is ak-dimensional vector, whilekpresents the dimension about input data. The position of the particle in thek-dimensional space presents a test case. The velocity of the particle affects the update of particle’s position. Each time, the position is updated by adding the distance passed by the unit time to the old position vectorvi. Clearly, the attribute of velocity is the most important direct factor that influences the particle’s position with updated iteration.

The two basic steps: Step 1 and Step 2 in Algorithm 1 are the basic procedures of PSO[21]modified to solve ATDG-PC. Letvandxbe the particle’s vector for velocity and position,nbe the input dimension about the test program, andKbe the population size of particle.pBestiis the historical best position of thei-th particle while thegBestrepresents the best-so-far particle position in the swarm. According to the parameter setting, χ is the inertia weight of former position.r1andr2are float random numbers in the range of [0,1].There are three important parameters which enhance the performance about the particle swarm optimization:

(1) The inertia weight of former position χ. (2) The weight of the difference value between particle’s best position and current positionc1. (3) And the weight of the historical best position reduces the current positionc2.

We compared the performance among different parameter settings. Finally, we found that the combination ofχ=0.4,c1=2,c2=1.5 achieved the best performance. In the following experiment, we will employ this parameter setting.

The procedure of PSO-CSC is provided in Step 3, whereτis a positive integer. The convergence speed controller examines the particle convergence condition everyτtimes. Condition I is to deal with the premature situation, and Condition II is implemented when the PSO converges too slowly.

3.2 Rule I and condition I for path exploration

The premature of particles is evaluated by the cosine similarity between two selected particles. In Condition I, the CSC framework will randomly select two particlesaandbin swarm when the cosine similarity value is greater than presetδ1. Meanwhile, not all the paths are covered. The position of the particles should be reset randomly, the velocity should be initialized to zero. The cosine calculation equation is listed as follows:

(3)

ConditionI:cos(Xa,Xb) >δ1

(4)

whereδ1is a threshold value indicating the particle similarity which is in the range of (0, 1). When the Condition I is satisfied, Rule I is triggered for path exploration. However, some heuristic attributes such aspBest1,…,pBestkandgBestare not modified. Hence, Rule I is likely to slow down the convergence speed without losing the searching ability of PSO.

The pseudo-code of Rule I which is contained in Step 3 of Algorithm 1 is presented as follows:

Algorithm2：PSO⁃CSCRuleI Input：X1，…，XK；V1，…，VK；pBest1，…，pBestKandgBest Output：newX1，…，Xk；newV1，…，VK；unchangedpBest1，…，pBestKandgBest1 foreachparticlei∈{1，2，…，K}do2345 foreachdimensionj∈{1，2，…，n}do xji←random(xjmin，xjmax)；vji←0； end6 end

Although Rule I seems to have no difference with population initialization. The most important heuristic informationpBest1,…,pBestkandgBestare saved. The new initial population will not search randomly. Instead, those heuristic information will help to quickly search the new initial population. The new particles converge around the historical best solution, the optimum solution may be close to the old local optimal solution.

3.3RuleIIandConditionIItoexploituncoveredpaths

Rule II is designed to accelerate the convergence speed when the global attractor convergence speed need to be accelerated. In the judgement of Condition II, we need to record the computational timetand a sequence ofgBest(t) string, wheret=NτandN= 1, 2,…. Therefore, the judgement of Condition II is presented as follows:

ConditionII:f(gBest(t-τ))-f(gBest(t))<

δ2|f(gBest(t-τ))|

(5)

whereδ2> 0 is a threshold value to measure the difference of evaluation function. Because thegBest(t) is the particle with the greatest function value aftertiterations, it always holds thatf(gBest(t-τ))≥f(gBest(t)). Hence, the left side of Expression (5) is more than or equal to zero.

The pseudo-code of Rule II which is contained in Step 3 of Algorithm 1 is presented as follows:

Algorithm3：PSO⁃CSCRuleIIInput：X1，…，XK；V1，…，VK；pBest1，…，pBestKandgBestOutput：newX1，…，Xk；newpBest1，…，pBestKandgBest；unchangedV1，…，VK1 foreachparticlei∈{1，2，…，K}do2345678 foreachdimensionj∈{1，2，…，n}do xji←gBestj+N(0，σj)； end pBesti=Xi； iff(pBesti)>f(gBest)then gBest=gBesti end9 end

Rule II reveals whether the evaluation function value has a significant improvement in a cycle ofτgenerations. When the Condition II is satisfied, the Rule II is applied to accelerate the convergence speed for exploiting uncovered paths. Thej-th dimension of thei-th particle of the swarm should be reset bygBestj+ N (0,σj), and thepBestof each particle and thegBestof the swarm are updated. The standard deviation of the normal distribution is adaptively changed by the following equation:

(6)

The reason we used Expression (6) is based on an assumption that the probability of a global optimal solution near the current optimal solution is greater than that near the lower quality solution. The new population generated by Rule II is restricted to a certain range ofgBest. And this certain range is determined by the fitness ofgBest. The higher the fitness value is, the closer the new population is togBest.

4 Experiment result

4.1 Benchmark functions

In this section, we present the experimental results to verify the effectiveness of the PSO with convergence speed controller for the ATDG-PC problem. Five classic benchmark functions[29]of cloud computing are chosen for the experiment. The five programs are commonly used in the research field of cloud and fog computing. For example, “Word Check” is a useful program in dealing with large amount of datum; “Word Count” is an important task in the field of cloud; “Sort”, “Table Association” and “String Verify” are widely implicated in the field of cloud computing. “Trie Tree”[30]is a program related to a data structure of cloud computing. The detailed information of the benchmark problems for the test data generation is listed in Table 2.

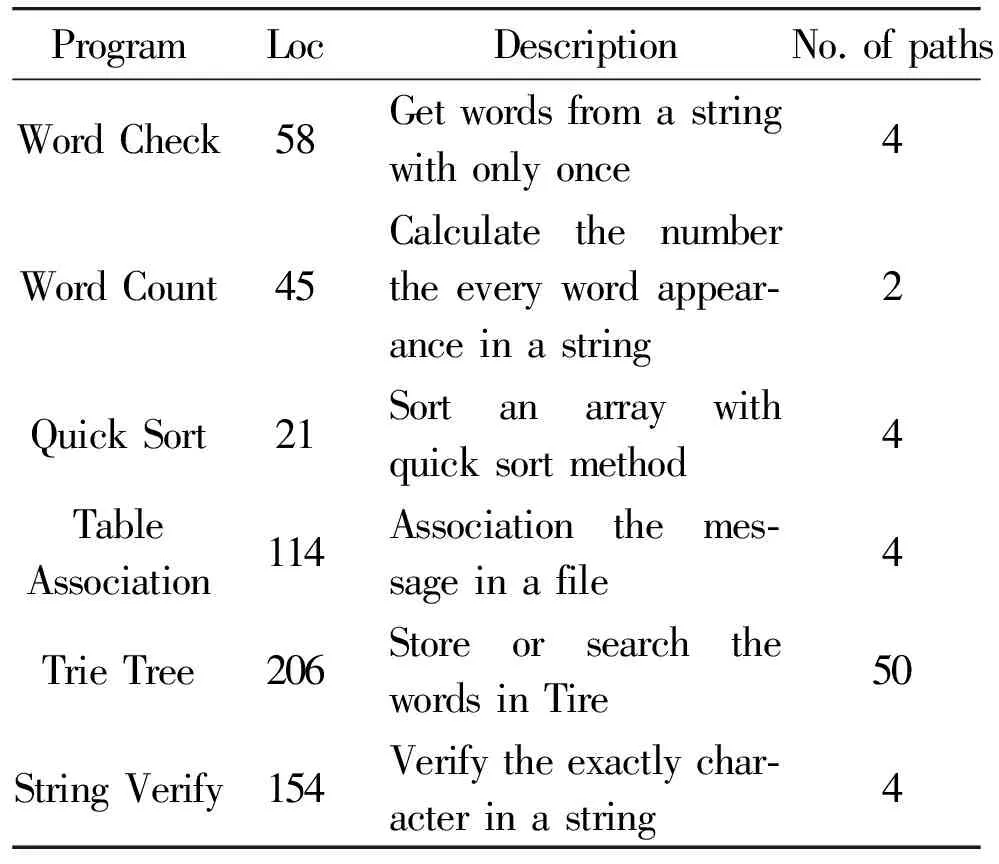
Table 2 Tested programs

* Loc presents the line number of each testing problem.

Path coverage is the most effective white-box test technique. We note that it is a challenge to generate test suite for covering all paths. We choose the overhead of effective test cases which are used to cover all the paths in order to evaluate the performance of each compared algorithm. The experiment does not use the running time as a benchmark comparing criterion because the running time is sensitive to the working environment. Therefore, it is difficult to compare each algorithm in the criterion of running time.

4.2 Experiment setting

In the experiment, PSO-CSC is compared with other three kinds of algorithms, including the PSO[21], ABC[1], and the common random search strategy. All of the meta-heuristic algorithms are strictly implemented following the same parameter setting. There are two terminal criteria in our experiments. The first criterion is to generate the test cases which cover all the paths. The second criterion is the overhead of test cases which exceeds the preset value. This preset number of maximum test case is 108. All of the parameters of PSO-CSC are listed in Table 3.

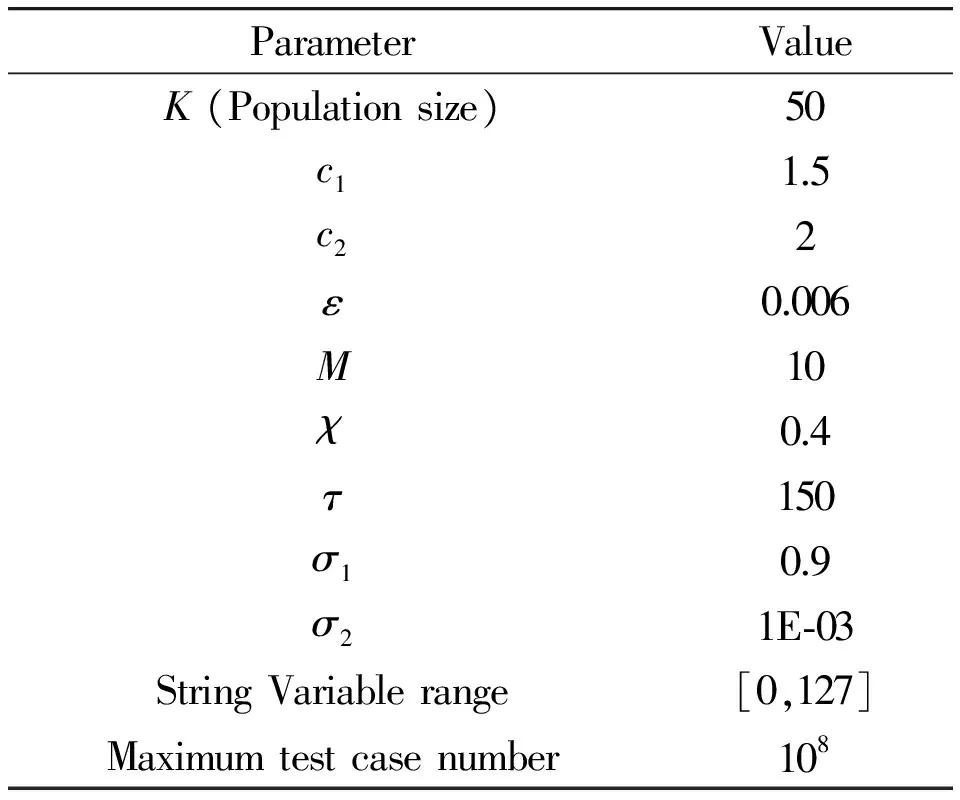
Table 3 Parameters of PSO-CSC

There are six test problems listed in Table 2. Considering that the input of four test problems is formed by the character string. The ASCII code is used to present each input character. The input range of each character is [0,127]. Each string is formed by a list of integers. In contrast, the input of “Sort” is a list of integers in the range of [1,100]. We encode all the input values of the test problems to a series of integer number that the fitness function can be introduced in section 2. If the real number is taken as the input value, the cost of all strategies will be particularly large. All the input values are positive integers considering the accuracy and consuming.

4.3 Experimental results

In our experiment, each program runs 30 times for each benchmark test program with the same parameter settings, while the test case consumption of each run for each algorithm is recorded. The experimental results are listed in Table 4, “Average” is the average value of test cases consumption. “Std” is the standard deviation of test case consumption. Considering the “Average” cost value that commonly has the magnitude of difference, we do not need to make significant analysis in the experiment. S.rate is on behalf of the rate that the algorithm covers all paths within the maximum test case number.

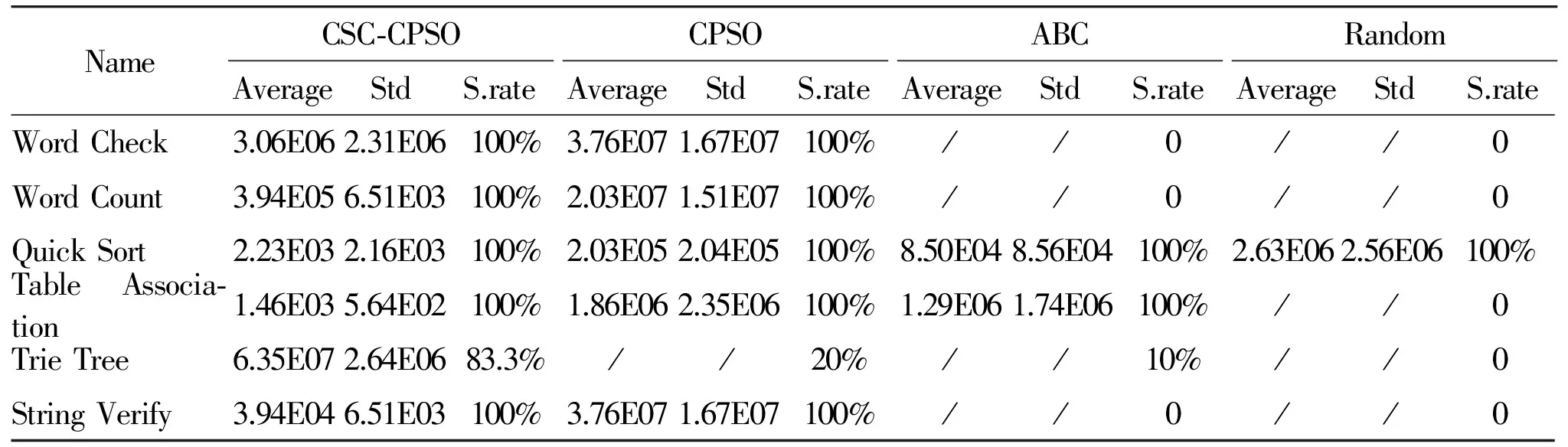
Table 4 Comparing results of six tested programs

The number of test cases used to implement the 100% path coverage(ATDG-PC) of the test problem was the evaluation criterion for each algorithm. The meta-heuristic algorithm we chosen to compare would be evaluated for each generation. In our experiments, we do not select time consumption as our standard. Because time consumption is affected by the operating environment and many other factors. The time consumption of the problem would be influenced by the running processes and operation system even under the identical configurations of the machine.

As we can see from Table 4, PSO-CSC has good performance in all the test problems. First, only PSO-CSC and PSO two algorithms could achieve 100% path coverage in the test problem “Word Check”, “Word Count” and “String Verify”. In contrast, the artificial bee colony algorithm (ABC) and stochastic strategy (Random) did not even achieve 100% path coverage once. Although both the PSO-CSC and PSO meet the coverage criterion in each trial, the PSO-CSC uses less test case consumption. Especially in the test problems of “Word Count” and “String Verify”, the average cost of PSO-CSC has magnitude of difference with the average cost of the PSO. Second, three meta-heuristic algorithms can achieve 100% path coverage for 30 trials in the test problems of “Quick Sort” and “Table Association”. And our proposed PSO-CSC uses the minimum average cost of the test cases. We can see that the overhead of PSO-CSC has magnitude of difference with other strategies. Our proposed PSO-CSC strategy was able to achieve 100% path coverage for 30 trials with 83%*30 =24 times in the test problem “Trie Tree”. While the PSO algorithm with the best performance in other strategies had only 20% success rate. That means other algorithms could achieve 100% path coverage within the maximum number of test cases just 6 times for 30 trials.

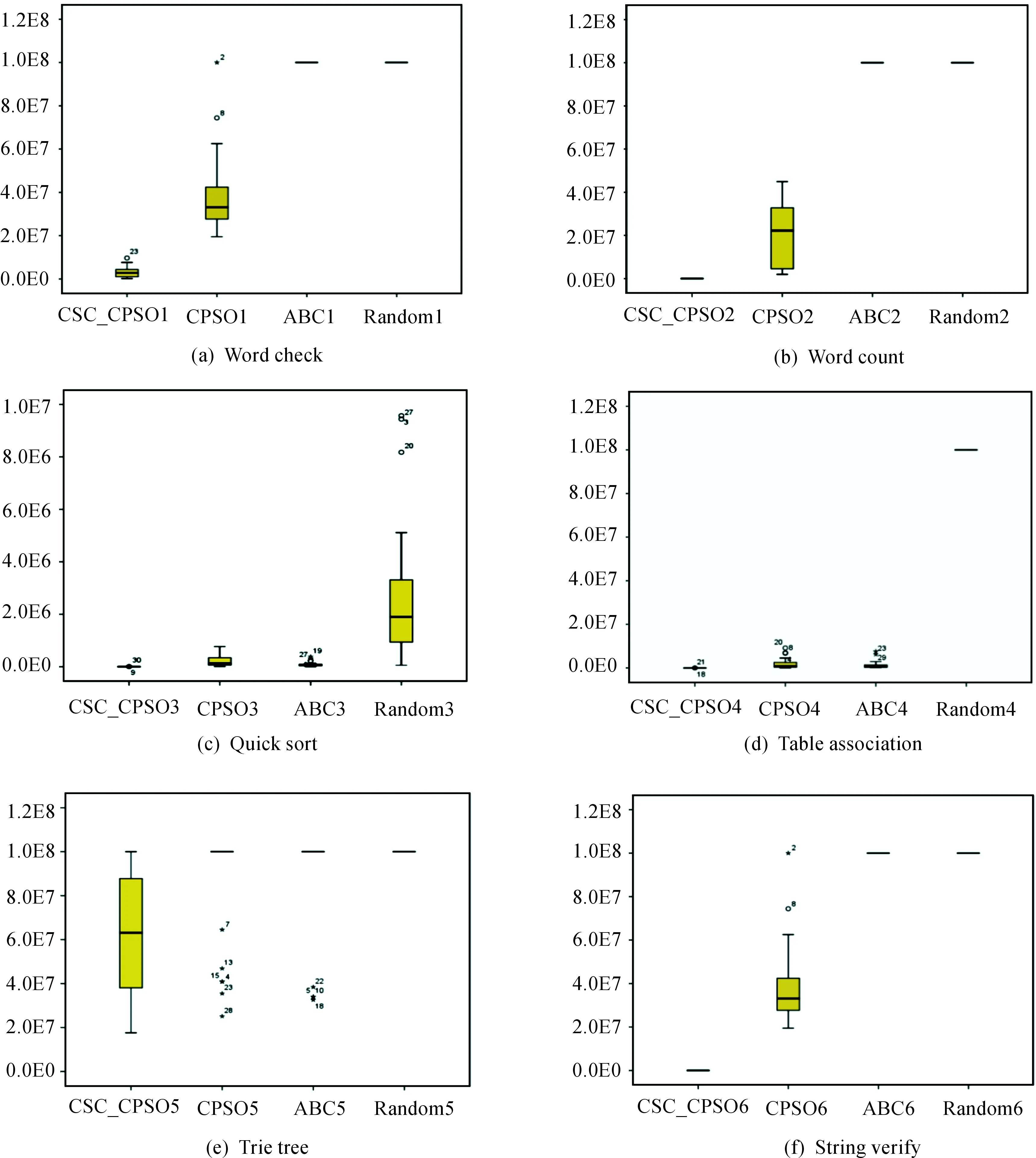
Fig.1 Plot boxes of the test cases number for benchmark functions.

1There are four comparing strategies in those plot boxes, i.e., PSO-CSC, PSO, ABC and Random from left to right.

2Each row below a test problem, they are Word Check, Word Count, Quick Sort, Table Association, Trie Tree and String Verify from (a) to (f).

Fig. 1 depicts the distribution of test cases overhead for comparing algorithms. Fig. 1 shows that the PSO-CSC’s test cases consumption are much smaller than PSO algorithms in sub-figure (a),(b) and (f). Other strategies like ABC and Random can not achieve 100% path coverage. PSO’s cost of test cases is relatively scattered. As we can see, the median of PSO-CSC’s data distribution was much smaller than that of the PSO. In the test problem of subfigure (c) and (d), PSO-CSC, PSO and ABC could achieve 100% path coverage. And the difference between different strategies is not significant. In fact, Table 4 shows that PSO-CSC’s overhead is significantly smaller than that of other algorithms. We can see from the subfigure (e) that PSO-CSC could achieve 100% path coverage for most times in the test problem “Trie Tree”. While the PSO and ABC were only achieving 100% path coverage several times in the test problem “Trie Tree”. It is clear that the proposed CSC strategy could greatly help the PSO overcome premature convergence problem and found the optimal solution.

In summary, the aim of this research is using convergence speed controller to improve the effectiveness of the PSO for ATDG-PC problem in the field of cloud computing. Good performance of the PSO-CSC should be attributed to the two rules of the convergence speed controller. Rule I avoided the premature convergence of PSO. Rule II accelerated the converge speed of PSO when the population was converged too slowly. The experiment results show that our method can efficiently help PSO to utilize useful heuristic information. Our method can achieve the best coverage rate within the minimum number of test cases.

5 Conclusion

In this paper, the convergence speed controller was applied to improve the particle swarm optimization’s ability for solving automated test data generation problem. The CSC framework was designed to slow down the convergence speed of PSO when it was trapped in local optimum. CSC also helps PSO to accelerate the convergence when it converged too slowly. The CSC helps the PSO to adaptively utilize the heuristic information to search for the uncovered paths. We record the number of test cases for covering all of the paths. The experiment result reveals that our method can stably use very low test case consumption to cover all the paths. The successful use of CSC to improve PSO’s performance for ATDG-PC problem boosts our confidence in applying CSC in other meta-heuristic algorithms. Since CSC is an additional operator, it can be added to other heuristic algorithms. In our future works, we will design the suitable CSC framework for differential meta-heuristic methods.

AcknowledgmentThis work is supported by National Natural Science Foundation of China(61370102), Guangdong Natural Science Funds for Distinguished Young Scholar (2014A030306050), the Ministry of Education-China Mobile Research Funds(MCM20160206) and Guangdong High-level personnel of special support program(2014TQ01X664).

[1]D.J.Mala, V.Mohan, and M.Kamalapriya, Automated software test optimisation framework an artificial bee colony optimisation-based approach,IetSoftware, vol.4,no.5, pp.334-348, 2010.

[2]B.Korel, Automated software test data generation,IEEETransactionsonSoftwareEngineering,vol.16,no.8, pp.870-879, 1990.

[3]J.R.Horgan, S.London, and M.R.Lyu, Achieving software quality with testing coverage measures,Computer, vol.27, no.9,pp.60-69, 1994.

[4]W.Miller and D.L.Spooner, Automatic generation of floating-point test data,IEEETransactionsonSoftwareEngineering, vol.2, no.3, pp.223-226, 1976.

[5]L.A.Clarke and A system to generate test data and symbolically execute programs,IEEETransactionsonSoftwareEngineering, SE-2 (3), pp.215-222, 1976.

[6]N.Tracey, J.Clark, and K.Mander, The way forward for unifying dynamic test-case generation: The optimisation-based approach, inInternationalWorkshoponDependableComputingandItsApplications,pp.169-180, 1994.

[7]A.Bouchachia, An immune genetic algorithm for software test data generation, inInternationalConferenceonHybridIntelligentSystems, pp.84-89, 2007.

[8]J.Kempka, P.Mcminn, and D.Sudholt, Design and analysis of different alternating variable searches for search-based software testing,TheoreticalComputerScience,605 (C),pp.1-20, 2015.

[9]X.J.YAO and D.W.GONG, Test data generation for multiple paths based on local evolution.,ChineseJournalofElectronics,24(CJE-1), pp.46-51,2015.

[10] Y.Cao, C.Hu, and L.Li, Search-based multi-paths test data generation for structure-oriented testing., inGeneticandEvolutionaryComputationConference,GecSummit2009,Proceedings, Shanghai, China, pp.25-32, 2009.

[11] S.Ali, L.C.Briand, H.Hemmati, and R.K.Panesar-Walawege, A systematic review of the application and empirical investigation of search-based test case generation,IEEETransactionsonSoftwareEngineering,vol.36, no.6,pp.742-762, 2011.

[12] M.Bohme and S.Paul, A probabilistic analysis of the efficiency of automated software testing,IEEETransactionsonSoftwareEngineering,pp.1-1, 2015.

[13] J.C.Lin and P.L.Yeh, Automatic test data generation for path testing using gas,InformationSciences,vol.131,pp.47-64, 2001.

[14] L.Wang, Y.Zhai, and H.Hou, Genetic algorithms and its application in software test data generation, inInternationalConferenceonComputerScienceandElectronicsEngineering, pp.617-620, 2012.

[15] Y.Suresh and S.K.Rath, A genetic algorithm based approach for test data generation in basis path testing,ComputerScience,2014.

[16] N.Zhang, B.Wu, and X.Bao, Automatic generation of test cases based on multi-population genetic algorithm,InternationalJournalofMultimediaandUbiquitousEngineering,vol.10,no.6, pp.113-122, 2015.

[17] R.Ding, X.Feng, S.Li, and H.Dong, Automatic generation of software test data based on hybrid particle swarm genetic algorithm,ElectricalandElectronicsEngineering, pp.670-673, 2012.

[18] M.R.Girgis, A.S.Ghiduk, and E.H.Abdelkawy, Automatic data flow test paths generation using the genetical swarm optimization technique,InternationalJournalofComputerApplications,vol.116,no.22, pp.25-33, 2015.

[19] P.R.Srivastava, V.Ramachandran, M.Kumar, G.Talukder, V.Tiwari, and P.Sharma, Generation of test data using meta heuristic approach, inTENCON2008-2008IEEERegion10Conference, 2008, pp.1-6.

[20] D.J.Mala, M.Kamalapriya, R.Shobana, and V.Mohan, A non-pheromone based intelligent swarm optimization technique in software test suite optimization, inInternationalConferenceonIntelligentAgentandMultiAgentSystems, 2009, pp.1-5.

[21] B.Y.Shi and R.Eberhart, A modified particle swarm optimizer,in 1998 IEEE International Conference on Evolutionary Computation Proceedings.IEEE World Congress on Computational Intelligence, 2010, pp.69-73.

[22] J.J.Liang, A.K.Qin, and S.Baskar, Comprehensive learning particle swarm optimizer for global optimization of multimodal functions,IEEETransactionsonEvolutionaryComputation, vol.10,no.3,pp.281-295, 2006.

[23] Z.Zhan and J.Zhang, Adaptive particle swarm optimization,IEEETransactionsonSystemsManandCyberneticsPartBCyberneticsAPublicationoftheIEEESystemsManandCyberneticsSociety,vol.5579,no.6,pp.202-211, 2011.

[24] A.Ratnaweera, S.K.Halgamuge, and H.C.Watson, Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients,IEEETransactionsonEvolutionaryComputation,vol.8,no.3, pp.240-255, 2004.

[25] J.J.Liang and P.N.Suganthan, Dynamic multi-swarm particle swarm optimizer, inSwarmIntelligenceSymposium, 2005,2005, pp.124-129.

[26] V.D.B.Frans and A.P.Engelbrecht, A convergence proof for the particle swarm optimiser,FundamentaInformaticae,vol.105,no.4,pp.341-374, 2010.

[27] M.Schmitt and R.Wanka, Particle swarm optimization almost surely finds local optima, inConferenceonGeneticandEvolutionaryComputation,2013, pp.57-72.

[28] R.Eberhart and J.Kennedy, A new optimizer using particle swarm theory, inInternationalSymposiumonMICROMachineandHumanScience, 1995,pp.39-43.

[29] L.Chuck, Hadoop in Action,PostsandTelecomPress, 2011.

[30] J.Shu, X.Sun, L.Zhou, and J.Wang, Efficient keyword search scheme in encrypted cloud computing environment,InternationalJournalofGridandDistributedComputing,2014.

HanHuangreceived the B.Man.degree in Applied Mathematics, in 2002, and the Ph.D.degree in Computer Science from the South China University of Technology (SCUT),Guangzhou, in 2008.Currently, he is a professor at School of Software Engineering in SCUT.His research interests include evolutionary computation, swarm intelligence and their application.Dr.Huang is a senior member of CCF and member of IEEE.XueqiangLireceived the Ph.D.degree in computer application technology from the South China University of technology, Guangdong, China,in 2012.He is a lecturer of the Faculty of Information Engineering in Guangdong Medical University since 2012.His research interests include Evolutionary algorithm, multi-objective optimization and other metaheuristics for solving two-echelon vehicle routing problems.

ZhifengHaoreceived the B.Sc.degree in mathematics from Sun Yatsen University, Guangzhou, China, in 1990, and the Ph.D.degree in mathematics from Nanjing University, Nanjing, China, in 1995.He is currently a Professor with the School of Computer, Guangdong University of Technology, Guangzhou, and the School of Mathematics and Big Date, Foshan University, Foshan, China.His current research interests include various aspects of algebra, machine learning, data mining, and evolutionary algorithms.

2016-12-20; accepted: 2017-01-20

the B.E.degree in Software engineering from South China University of Technology, Guangzhou, China, in 2016.He is currently a postgraduate student majored in software engineering in School of Software Engineering, South China University of technology, Guangzhou, China.His current research interests include automated software test case generation and evolutionary computation for software testing.

•Fangqing Liu, Han Huang are with School of Software Engineering, South China University of Technology, Guangzhou 510006,China. E-mail: 564376030@qq.com; hhan@scut.edu.cn.

•Xueqiang Li is with School of Information Engineering, Guangdong Medical University, Dong Guan 523808, China. E-mail: lxqchn@163.com.

•Zhifeng Hao is with School of Mathematics and Big Data, Foshan University, Foshan, P. O. Box, China. E-mail: zfhao@fosu.edu.cn.

*To whom correspondence should be addressed. Manuscript