A Multi-Objective Evolutionary Approach to Selecting Security Solutions

Yunghee Lee, Tae Jong Choi, and Chang Wook Ahn

AMulti-ObjectiveEvolutionaryApproachtoSelectingSecuritySolutions

Yunghee Lee, Tae Jong Choi, and Chang Wook Ahn*

In many companies or organizations, owners want to deploy the most efficient security solutions at a low cost. In this paper, we propose a method of choosing the best security solution from various security solutions using multi-objective genetic algorithm considering cost and weakness-decrease. The proposed system can support the best security solutions in various aspects of security issues. We use the NSGA-II algorithm, which has been verified in a variety of fields, to provide a comparison with existing genetic algorithms. Our scheme has increased the dominant area by more than 30% compared with the previous scheme and can provide a more diverse solution set.

security; evolutionary algorithm; multi-objective genetic algorithm; artificial intelligence

1 Introduction

As the information technology systems and the Internet grew, so did the number of malicious threats to information[1]. To prevent information threats like this, organizations and enterprises study security solutions to secure information separately from their usual work. Security solutions are generally physical and logical countermeasures to prevent the failure and destruction of the information systems[2]. But in most cases, companies do not want to spend a lot of money on improving security. Because investing in security solutions does not seem to be effiective in a short time. Moreover, in order to invest in security solutions, companies have to choose how much to invest in what measures, but it is very difficult to make such a choice without knowing the exact threats and the effiectiveness of countermeasures. In this paper, we describe the selection of a security solution using NSGA-II, a kind of multi-objective genetic algorithm. This will help any business or organization easily choose the best security solution. This paper is organized as follows. In Section 2, we talk about genetic algorithms (GA) and Pareto-optimization. In Section 3, we explain a multi-objective genetic algorithm. We design a creating security solution and Weakness Decrease Point (WDP) for experiment and explain the program code in Section 4. The system we propose is presented in Section 5. Section 6 concludes the paper.

2 Related works

In this section, we talk about Pareto-optimality after the simple description of genetic algorithm and knapsack problem.

2.1GeneticalgorithmandKnapsackProblem

Genetic algorithm is a kind of heuristic search based on the phenomenon of nature. It was firstly designed by John Holland in 1975. This is one of the techniques to solve the optimization problem by calculation based on the natural evolutionary process. In general, if it is impossible to obtain an optimized solution of a problem through a formal formula, or if it is too complicated, it may be efficient to solve the problem through a genetic algorithm. However,the genetic algorithm does not always find a global optimal solution. This only helps to find solutions that are close to the optimal solution in a short time. Therefore, genetic algorithms are generally useful for problems classified as non- deterministic polynomial (NP) time problems[3].

The knapsack problem is one of the most suitable problems to solve with genetic algorithm. The knapsack problem is a matter of finding out what items we need to fill the bag to make it the most valuable. The size of the items that can be stored in the bag is fixed, and each item has a predetermined value and size. Therefore, if the item can be split, we can easily find the global optimal solution to this problem with the greedy algorithm. But if they can not break apart, this problem can not be solved with a formal formula. Thus, in this case, this problem becomes an NP-completeness problem[4,5]. If we use a genetic algorithm to solve the knapsack problem, we can find an efficient solution for a short time. Recently, various studies related to the research we are trying to do have been preceded[6].

2.2 Pareto-optimality

If you use a simple genetic algorithm to solve the knapsack problem, the sum of the sizes will naturally approach the maximum size. If you have a budget and do not have any problems with using your whole budget, you can solve this problem using the simple genetic algorithm. But companies and organizations want to find low-cost, high-efficiency solutions and deploy it. Therefore unlike a simple genetic algorithm that considers only one objective, in the real world, it is necessary to find the optimal solution considering both the cost and the WDP. Sometimes, a problem may have more than just two objectives. If that happens, the problem will be much more complicated than when considering only one objective. In this paper, we propose a method to solve the problem by considering two objectives: cost and WDP.

In general, we use the concept of “Pareto-optimality” when there are multiple objectives to find the global optimal solution of the problem. For example, the cost and WDP of security solutions to address security flaws are shown in Table 1. As shown in Fig.1, the data in Table1 can be charted. In the Fig.1, the X axis represents (100-cost) and the y axis means WDP: Decrease of dangerous.

In the Fig.1 the solution in the upper right is observed to be more effiective and better.The optimal solution is the top-most, right-most solution in the chart. However, in general, higher WDPs result in higher costs, making it difficult to find the ideal solution like that. Instead, we can find a Pareto- optimal that is superior to other solutions[7]. The squares on the chart show Pareto-dominance easily. For example, R2 has a very high WDP, which is very helpful in solving security problems, but solution R2 is not an optimal solution because there is a solution R5 with a lower cost and higher WDP. At this point, Solution R2 is said to be a Pareto-dominated entity. When we create a chart like the one shown in the Fig.1, we call the unconstrained solution Pareto-optimal for any other solution, and call the set a Pareto-optimal set. The line that the pareto-optimal set forms is called the Pareto-frontier. Ultimately, what we are looking for is a Pareto-optimal set.

Table 1 The list of solution sets that generated randomly.

Fig.1Charttoselectbestsolutionfromvariouscandidates.

3 Multi-objective genetic algorithm:NSGA-II

There are many kinds of multi-objective genetic algorithms (MOGA) to solve many types of problems: NPGA, NSGA, SPEA, etc. All of them are very popular MOGA solutions and in this paper, we use the NSGA-II algorithm for solving the problem. Because NSGA-II is the lightest and fastest method of MOGA known so far. NSGA-II is a new advanced technique compared with NSGA, a conventional multi-objective genetic algorithm. It can finish the cal- culation in less time than NSGA and introduces the concept of non-dominant ranking. In addition, NSGA-II introduced a concept called Crowding Distance.Therefore, this scheme can distribute resources more efficiently than existing algorithms. Another thing that NSGA-II is diffierent from NSGA is Elitism. Elitism is the scheme of keeping the superior population among the population to the next generation. Therefore, solutions with a high fitness are not easily lost through generations[8]. The NSGA-II algorithm is easy to use and can quickly find solutions with a high fitness. And it has very high performance so that this algorithm is very popular[9].

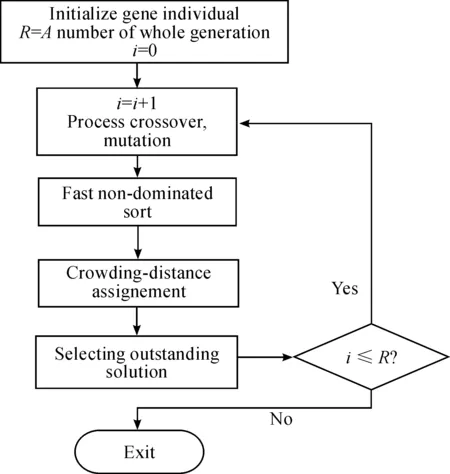
Fig.2 Flowchart for NSGA-II algorithm.

The NSGA-II algorithm is shown in Fig.2[10]. Non-dominated rand means the rank that how many other solutions are dominating the solution. In other words, a lower non-dominated rank is a better solution. For example, there is a solution named A. If any solution is a dominating solution A, the non- dominated rank of solution A is zero. Thus, in the same generation, the Pareto optimal solution has the highest priority, and the solution farther from it has an increasingly lower priority. Like this, the non-dominated rank alignment process allows solutions to converge on the Pareto-optimal set. And Crowding Distance is a solution to see how many solutions are gathered in a small area when the charts are shown like Fig.1. This is a value that is calculated to help the solutions with the same non-dominated rank have diversity. Each solution has a high Crowding Distance value if it is less similar to the neighboring solution. This is an element for selecting an object with a diffierent property from the set of genetic entities belonging to the same non-dominated rank[8].

3.1 Performance improvement

We used diffierent mutations and crossover types to improve performance. Mutation and crossover are very important components in the genetic algo rithm. There are many types of mutation and crossover: Uniform Mutation, Parent-Centric Crossover, Bit Flip Mutation, Half-Uniform Crossover and etc. In this paper, we use the Simulated Binary Crossover (SBX) for crossover process and Polynomical Mutation (PM) for mutation process in NSGA-II. SBX is the operator that has the search ability similar to that of a single-point binary-coded crossover operator[11]. And the PM is the operator that is widely used in evolutionary optimization algorithms as a variation operator[12]. It attempts to simulate the offispring distribution of binary-encoded bit-flip mutation on real-valued decision variables. In this paper, the type of the value to be calculated was binary, but we used PM because the PM showed better performance than the bit flip mutation. PM is similar to SBX, it favors offispring nearer to the parent[13].

And we set the population size for the genetic algorithm to 500 and the number of generations to 15000.

4 Creating security solution and WDP

We need to create a variety of virtual security solutions for the experiment, each with an introduction cost and a WDP. However, WDP is a value that can not be easily quantified. Therefore, in this paper, we use a reasonable random number as a WDP to create a sample virtual security solution.

First, we need to create 500 random numbers to be used as the cost of introducing a virtual security solution. The total sum of 500 random numbers is 1000000. After doing that, we sort 100 random random numbers and put them into the array arr [ ]. Then we use the source code below to create a WDP corresponding to each cost, and place it in the array arr2 [ ].

for (i=0;i<500; i++)

{

arr2[i]=gaussianRand(arr[i], STD);

// STD is the standard deviation of gaussian random function

// We setted STD to 50

if (arr2[i] <=0)

arr2[i] = rand()% arr[i] +1;

}

double gaussianRand(double mean, double stddev)

{ // gaussian random number generater function static double n2= 0.0;

static int n2_cached = 0;

if (!n2_cached)

{

doublex,y,r;

do

{

x=2.0*rand()/RAND_MAX-1;

y=2.0*rand()/RAND_MAX-1;

r=x*x+y*y;

} while (r==0.0 ||r> 1.0);

{

double d=sqrt(-2.0*log(r)/r);

double n1=x*d;

n2=y*d;

double result = n1*stddev + mean;

n2_cached = 1;

return result;

}

{

else

{

n2_cached= 0;

return n2*stddev+ mean;

}

}

So we can make the meaningful random WDP. Weakness decrease point will almost be proportional to security solutions cost. But there can be rarely too high Weakness Decrease Pointcsecurity solutions cost or the opposite case.

5 Proposed scheme

In this section, we suggest techniques for selecting the best security solution using NSGA-II, the MOGA mentioned in the previous section. As we mentioned in Section 1, businesses and organizations want security solutions that can get the most out of their business with minimal cost. Park et al. have released a solution for this problem[14]. They tried to solve this problem using the simple genetic algorithm and used a list of 10 virtual security solutions in the experiment. In order to compare the two schemes, we have coded programs that perform as well as the simple genetic algorithms used in Park et al.’s paper[14], and have created more new virtual security solution lists and experimented. We compared the results obtained using our scheme with those obtained using Park et al.’s scheme[14]. As a result of using the scheme of Park et al.[14], we could find three optimal solutions.

And also important in the genetic algorithm is the fitness evaluation function. It is called as the fitness function. In the simple genetic algorithm used by Park et al.[14], the fitness function considers only one objective: WDP. In MOGA, however, we can use multiple objectives for fitness functions.

(1)

(2)

In this paper, we used two fitness functions as shown in Equations 1 and 2.Equation 1 uses (100000-the total cost of the solution) values for fitness calculations, and Equation 2 uses the entire WDP of the solution for fitness calculations.nis the number of the whole chromosomes, in other words,nmeans the number of solutions.vcmeans each chromosome structure.vc.dincludes the decrease point of security weakness, andvc.cincludes the cost for selecting that solution.vc.sincludes the binary number for checking whether each solution was selected or not selected. So ifvc.s’s value is 0, that means the solution was not selected.

Fig.3ThegraphaboutselectingsecuritysolutionusingNSGA-II.

Fig.3 compares the best virtual security solutions selected using the NSGA-II algorithm to the best virtual security solutions selected using the simple genetic algorithm. The horizontal axis indicates the value off1, and the vertical axis indicates the value off2. The results of using the existing Park et al.’s scheme[14]have reversed the cost value for easy comparison. Therefore, the cost of the original research is actually 100000 times the original cost. For the sake of clarity, we plotted the results of original research as red squares and the results of our research as black dots. Using the NSGA-II-based security solution selection scheme we have studied, we can confirm that the selected security solution set forms the Pareto-frontier and completely dominates the results of existing papers. The results of this paper provide a variety of choices, from low cost solution selection to high cost solution selection.

6 Conclusion

In this paper, we propose a scheme to efficiently select the security solutions required by corporations and organizations using NSGA-II in terms of various objectives: cost and value. The proposed method was able to find optimal solutions considering various objectives and showed superiority in the process and performance of fitness evaluation compared to existing papers using simple genetic algorithm. More detailed study on how to quantify the Weakness Decrease Point (WDP) should be conducted and the stability and performance of NSGA-III developed by NSGA-II should be verified.

Acknowledgment

This research was supported by X-Project funded by the Ministry of Science, ICT & Future Planning (NRF-2016R1E1A2A02946533) and also supported by Institute for Information & communications Technology Promotion (IITP) grant funded by the Korea government (MSIP) (No.B0717-17-0070).

[1]S.W.Chai, Economic effiects of personal information protection, Korea Consumer Agency,vol.33, pp.43-64,2008.

[2]Y.O.Kwon and B.D.Kim, The effiect of information security breach and security investment announcement on the market value of korean firms,InformationSystemReview, vol.9,no.1, pp.105-120, 2007.

[3]M.Mitchell,Anintroductiontogeneticalgorithms,USA: MIT press,1996.

[4]Kellerer and Hans,Knapsackproblems, Berlin, Germany: Springling Press,2004.

[5]S.Martello and P.Toth, Knapsack problems: Algorithms and computer implementations,JournaloftheOperationalResearchSociety, 42(6), 513-513.

[6]P.C.Chu and J.E.Beasley, A genetic algorithm for the multidimensional knapsack problem,Journalofheuristics,vol.4, no.1, pp.63-86, 1998.

[7]J.Horn, N.Nafpliotis, and D.Goldberg, A niched pareto genetic algorithm for multiobjective optimization, inProceedingsof1stIEEEConferenceonEvolutionaryComputation, Florida,USA,1994, pp.82-87.

[8]J.Yoon, J.Lee, and D.Kim, Feature selection in multi-label classification using nsga-ii algorithm,JournalofKIISE:SoftwareandApplications,vol.40,no.3, pp.133-140, 2013.

[9]K.Deb, A.Pratap, S.Agarwal, and T.Meyarivan, A fast and elitist multi objective genetic algorithm: Nsga-ii,IEEETransactionsonEvolutionaryCompution,vol.6,no.2,pp.182-197,2002.

[10] S.T.Khu and H.Madsen, Multi-objective calibration with pareto preference ordering: An application to rainfall-runoffi model calibration,WaterRe-wourcesResearch,vol.41,no.3,pp.1-14,2005.

[11] D.Kalyanmoy and K.Amarendra, Real-coded genetic algorithms with simulated binary crossover: studies on multimodel and multiobjective problems,ComplexSystems, vol.9,no.6,pp.431-454, 1995.

[12] M.Hamdan, A dynamic polynomial mutation for evolutionary multi-objective optimization algorithms,InternationalJounalonArtificialIntelligenceTools,vol.20,no.1,pp.209-219, 2011.

[13] K.Deb and D.Deb, Analysing mutation schemes for real-parameter genetic algorithms,InternationalJournalofArtificialIntelligenceandSoftComputting, vol.4,no.1,pp.1-28, 2014.

[14] J.Park, Y.Bang, G.Lee, and K.Nam, Generation of security measure by using simple genetic algorithm, inProceedingsofKIISEConference30, 2003,vol.21,pp.769-771.

TaeJongChoiis working as a postdoctoral researcherin at Sungkyunkwan University (SKKU), Republic of Korea. He received Ph.D. degree from the Department of Electrical and Computer Engineering at SKKU in 2017. His research interests include evolutionary algorithms, machine learning, deep learning, and the applications of artificial intelligence.ChangWookAhnis working as a Professor in the School of Electrical Engineering and Computer Science, Gwangju Institute of Science and Technology (GIST), Gwangju, Republic of Korea. From 2008 to 2016, he was an Assistant/Associate Professor at the Department of Computer Engineering, Sungkyunkwan University (SKKU), Suwon, Republic of Korea. He received his PH.D. degree from the Department of Information and Communications, GIST. His research interests include genetic algorithms, multi-objective optimization, neural networks, and the applications of evolutionary machine learning techniques.

2016-12-20; accepted:2017-01-20

B.S. degree from the Department of Cyber Security at Kyung-Il University, Kyungsan, Republic of Korea, in 2012. He is currently a M.S. candidate in the Department of Computer Engineering at Sungkyunkwan University, Suwon, Republic of Korea. Also, he is currently working as a researcher at Gwangju Institute of Science and Technology (GIST). His research interests include genetic algorithms, Artificial Intelligence, multi-objective optimization and the cyber security.

•Tae Jong Choi is with Department of Computer Engineering, Sungkyunkwan University, 2066, Seobu-ro, Jangan-gu, Suwon-si, Gyeonggi-do, Republic of Korea.

•Yunghee Lee and Chang Wook Ahn are with School of Electrical Engineering and Computer Science, Gwangju Institute of Science and Technology (GIST).E-mail: cwan@gist.ac.kr(Chang Wook Ahn).

*To whom correspondence should be addressed. Manuscript