A Common Strategy to Improve Community Detection Performance Based on the Nodes’ Property
2017-10-11WeiDuandXiaochenHe
Wei Du and Xiaochen He
ACommonStrategytoImproveCommunityDetectionPerformanceBasedontheNodes’Property
Wei Du and Xiaochen He*
In order to improve the community detection results, a novel strategy based on the nodes’ property is used for the detecting algorithm. For a given community structure of a network, the value of the modularity will be changed when a node is moved from one community to another. Accordingly, this new strategy readjusts the affiliation between a node and its community to get a bigger value of the modularity. The results of community detection for some classic networks, which are from Ucinet and Pajek networks, indicate that the new algorithm achieves better community structure (bigger value of modularity) than other methodologies based on modularity, such as Girvan and Newman’s algorithm, Newman’s algorithm, Aaron’s algorithm and Blondel’s algorithm.
community structure; networks; node;modularity
1 Introduction
Most of the social networks do not consist of an undifferentiated mass of nodes but have some subgroup structures. Within those subgroups, the network connections are denser and between them the connections are sparser. This complex characteristic of network is called community structure and has been one of the key objectives of network analysis in various domains such as sociology, biology and computer science, and has attracted considerable attention in complex network[1]. Community structure measurement and detection are two key issues in this research field. The modularityQdefined by Girvan and Newman is the milestone of community structure study and a suitable criterion for community structure measurement[2], although there are still some arguments[3,4]. Currently, community structure detecting methods have been the hot spot in many domains and disciplines[5].
According to the operation of the community splitting or combining during the detection process, the detection algorithms can be divided into three categories[6]: the first is a “top-down dividing” strategy, which firstly takes the whole network as a single community and then divides a big community into small subgroups repetitively[2,7]. The “top-down dividing” strategy needs to compute the edge-betweenness which has high computational complexity, and the modularity cannot be fully exploited either. Another is a “bottom-up merging” strategy, which treats each node as a community and then merges two small communities to form a big one[1,8-10]. This strategy overcomes the disadvantages of the former strategy, but different orderings of merging may lead to different detections. The third one is a “mixed optimizing” strategy, combining both advantages of the aforementioned two strategies. The heuristic methods by optimizing the modularity such as simulated annealing techniques[11]and genetic algorithm[12]are representative ones of this strategy. Each community structure detection algorithm mainly solves two problems synchronously: one is to set the number of network communities; the other is to rightly distribute the nodes to one of the communities. These two issues always correlate and influence each other.

For a given division community structure, this paper discusses the influence that the network node in different community may have, and put forward a simple mechanism based on this idea to modify the current community structure detection algorithms. The rest of the paper is divided into three parts. The second part is to introduce the mechanism of algorithm based on node characteristics after discussing the definition of modularity. The third part is to compare the community structure detection results between the improved algorithm and the existing algorithms using the classical network data, and to clarify the availability and validity of our improved algorithm. The fourth part is the conclusions and further researches.
2 The Algorithm

(1)


Fig.1Therelationshipbetweennodeiandthecommunities.
If nodeiis removed from communitypand set it as an independent community, the change of modularity can be computed by Equation (2):
(2)
Then by merging nodeiinto the communityq, the change of modularity can be computed by Equation (3):
(3)
By combining the above two operations together, i.e. removing the nodeifrom communitypand placing it in another communityq, the gain of the modularity (ΔQ) will become Equation (4):
ΔQ=ΔQp→i→q=ΔQi→q+ΔQp→i=
(4)
Obviously, if ΔQ>0, then the nodeilocated in communityqis more suitable than in communityp, and if the degree of nodei,di=1 or ΔQ<0, the nodeiwill stay in its original communityp.
The above analysis has discussed the effects by moving one node from one community to another community, while moving more nodes will have a similar effect because ΔQcan be superposed. In this paper, we mainly focus on moving nodes one by one. For a community structureτ(V) of a network, which is obtained by a detecting algorithm, such as Newman’s algorithm in ref[1], Bodel’s algorithm in ref[10], and so on, a common strategy based on the above discussion to modify the recent community detecting algorithms can be described as following briefly:

Algorithm:theframeworkofthenewalgorithmbasedonthenode’sproperty1: Input:COM(c),whichisthenodesetincommunityc,c=1,2,…m;2: repeat3: foreachnodeiinCOM(p)do4: computerΔQp→i→qaccordingtoequation4;5: ΔQq′←maxqΔQp→i→q;6: ifΔQq′>07: movenodeifromCOM(p)toCOM(q′);8: endif9: endfor10:untilc=m11:Output:COM
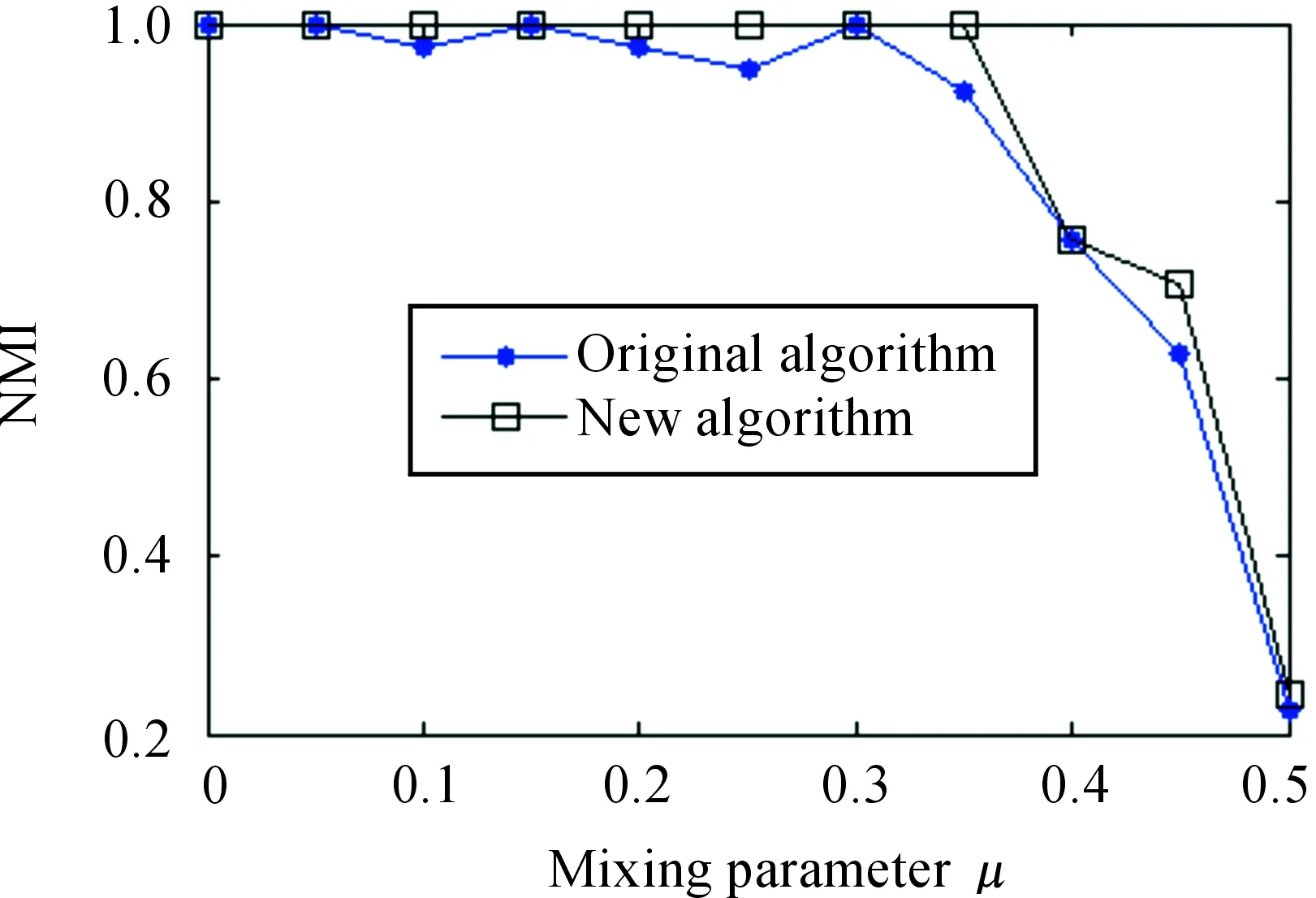
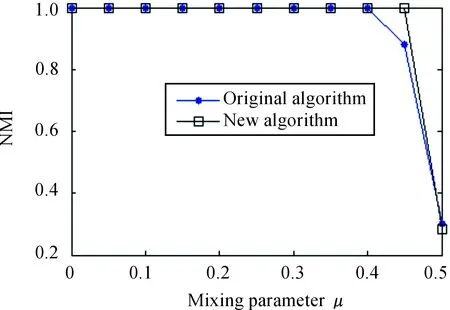
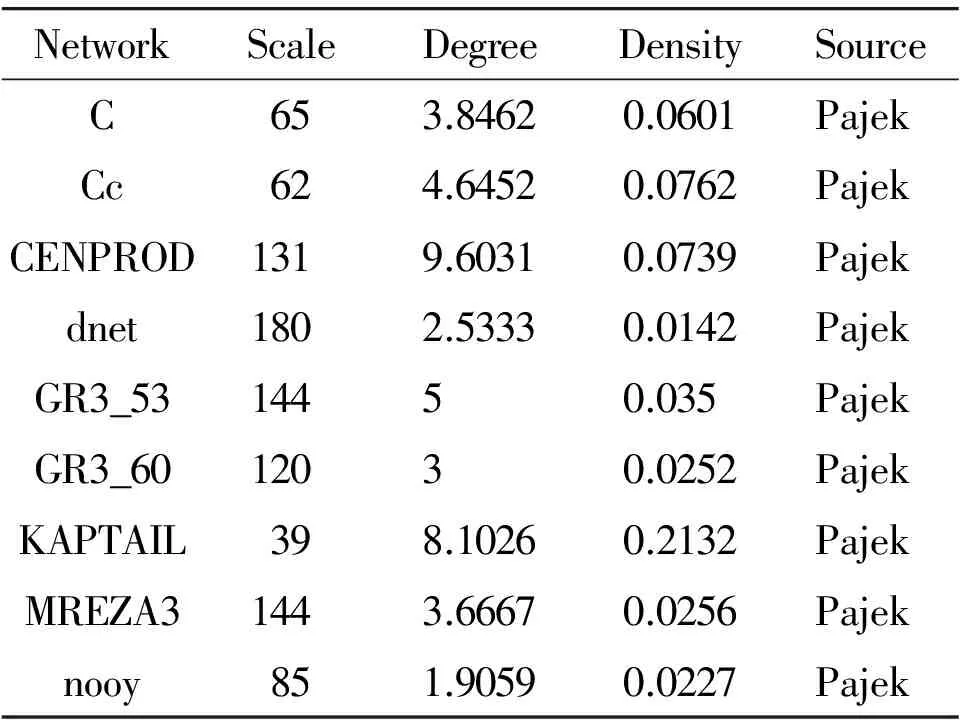
This new algorithm is performed based on the existing community structureτ(V)={V1,V2,…,Vm}. Hence, it can be used to improve the detection result acquired by any other detecting algorithm. Because the network has been separated tomcommunities, the new algorithm at most exploresn×mtimes. Due tom< In this section, four other algorithms are compared with the new algorithm. The first is Girvan and Newman’s algorithm (denoted as G) based on betweenness analysis with the complexity ofO(m2n), wheremis the number of network edges andnis the number of nodes[2]. The second is Newman et al.’s algorithm (denoted as N) based on modularity change costingO((m+n)n)[1]. The third is Clauset et al. algorithm (denoted as A) modified from N algorithms with the running timeO(mdlogn), wheredrepresents the depth of the dendrogram describing the community structure[8]. The fourth is heuristic method as proposed by Blondel et al. (denoted as B), and the complexity of which isO(n2)[10]. G algorithm is a typical “top-down dividing” strategy, while N, A and B algorithms are very popular “bottom-up merging” strategy. The G Algorithm results are obtained by Ucinet 6.212, and other experiments are run in Matlab 7.0 on a PC with IntelRCoreTM2 DUO CPU T6400 @2.00 GHz. 3.1 Computer-generated network In this paper, the computer-generated network in our experiment is a benchmark network proposed by Lancichinetti et al [17]. The network contains 128 nodes, four communities that each has 32 nodes. The degree of each node is 16, which is divided into inside-link and outer-link by a fractionμ. It can be expressed as Equation (5): kout=μki kin=(1-μ)ki (5) wherekoutis the links of nodeiwith the other nodes of the network, andkinis the links of nodeiwith the other nodes of its community. Whenμ<0.5, the links of a node connected nodes inside its group are more than the links connected nodes in other three communities. And this network was used to test the efficiency of the modified algorithm. A similarity measurement Normalized Mutual Information (NMI) described in[17] was used to estimate the efficiency of the modified algorithm by calculating the similarity between detecting community structure and actual community structure generated by computer. Its formula is expressed as Equation (6): (6) wherecA(cB) is the number of groups in partitionA(B),Ci(Cj)is the sum of elements ofCin rowi(columnj), andNis the number of nodes. IfA=B, thenI(A,B)=1, and it means that the algorithm can correctly detect the real partition of network; and with a smallerI(A,B), the efficiency of the algorithm is worse. And 11 different sets of computer-generated data were used as the experimental test data, with the mixing parameterμranging from 0 to 0.5. For eachμ, the corresponding NMI are generated by the average of 10 independent runs. Fig.2 shows the average NMI for A algorithm and its modified algorithm when the mixing parameter increases from 0 to 0.5. Fig.2NMIversusmixingparameterμforAalgorithmanditsmodifiedalgorithm. As shown in Fig.2, when the value of mixing parameterμis less than 0.35, the detecting result of A algorithm is unstable, but the result of modified algorithm can always find the correct community partition (NMI equal to 1). With the value of mixing parameterμincreases (μ>0.35), the community structure begins to become fuzzy. The NMI of the two algorithms are decreased significantly, which means that it is more difficult to detect the community structure by the two algorithms. But the detecting result from the modified algorithm is always superior to the result from the A algorithm, obtained a greater NMI. This feature can be shown in Fig.3, which is the NMI versus mixing parameterμforNalgorithm and its modified algorithm. But in Fig.3, whenμis greater than or equal to 4, the advantage of two algorithms begins to disappear. For example, whenμ=0.4, two algorithms get the same NMI value. This means that the detection result is the same. And for the subsequentμ, the difference between the two algorithms NMI value is still very small. Thus, when the community structure begins to be fuzzy, for N algorithm, the efficiency of the modified algorithm is not very obvious. Fig.3NMIversusmixingparameterμforNalgorithmanditsmodifiedalgorithm. Fig.4 shows the average NMI for B algorithm and its modified algorithm. Fig.4NMIversusmixingparameterμforBalgorithmandit’smodifiedalgorithm. As shown in Fig.4, the B algorithm and its modified algorithm can detect the correct community structure whenμ<0.4. And the modified algorithm can still correctly detect the community structure whenμ=0.45. And at this time, the community structure has become fuzzy, and is hard to be detected. It should be noted that whenμ=0.5 each node has half of its links with the other nodes of other communities. This means that the community structure is very fuzzy. So no matter what kind of algorithms can hardly find the actual partition of the network. 3.2 Standard Networks In order to analyze the applicability of the new algorithm, we tested the dolphins network, the lesmis network and some standard networks available in the social network analysis software, Pajek and Ucinet. The parameters for these networks are summarized in Table 1, where the original asymmetric networks are symmetrized. The modularity’s values of the community structure detecting results obtained from these four typical algorithms are shown in the column “Original algorithm” in Table 2 separately. And the corresponding results for the algorithm are shown in column “New algorithm” in Table 2. Table 1 Parameters for the classic networks. ① www-personal.umich.edu/~mejn/ NetworkScaleDegreeDensitySourceC653.84620.0601PajekCc624.64520.0762PajekCENPROD1319.60310.0739Pajekdnet1802.53330.0142PajekGR3_5314450.035PajekGR3_6012030.0252PajekKAPTAIL398.10260.2132PajekMREZA31443.66670.0256Pajeknooy851.90590.0227Pajek Note: For the standard network provided by Ucinet*http://www.analytictech.com/downloaduc6.htmand Pajek*http://vlado.fmf.uni-lj.si/pub/networks/pajek/default.htm, we have done symmetrical transform for the non-symmetric 0-1 network Table 2 The comparison between original algorithm and new algorithm. Note: G algorithm result was obtained by Ucient 6.212, the values of the modularity were calculated to three decimal places. “/” represents the algorithm that can’t provide result. *** means the correspondingp<0.001; ** means the correspondingp<0.01; * means the correspondingp<0.05; + means the correspondingp<0.1. There are different community detection results for the same network by using these four algorithms. According to the value of the modularity, B algorithm performs better than others. All the test results show that the new algorithm has significantly improved the original algorithms. Specifically, the new algorithm has improved the detecting results of 61.1% networks for G Algorithm, 61.1% for N algorithm, 77.8% for A algorithm, and 35.3% for B algorithm respectively. This paper presents an improved algorithm for community structure detecting based on the node features. Based on the known community division, the movement of a node in the network from one community to another may lead the change of the modularity value. The new algorithm based on this feature readjusts the affiliation of node and community in order to obtain the maximum modularity value, i.e. the new community structure. According to the experiments of representative detection algorithm for classic network data, we believe that our improved algorithm can optimize the community detection result of the original algorithm, and obtain a greater modularity without significant computation increscent. The community detection is an NP-hard problem. For a given network, theoretically, it is hard to obtain an optimal detection result of modularity. Thus, the improvement of the algorithm efficiency and the accuracy of precise results are always the important research problem in the community structure. It is a useful attempt that this paper proposed an improved algorithm based on the node feature. But our algorithm is a correction of other algorithm from which the community detection result is obtained. How to merge our algorithm to other algorithm, or how to effectively combine our improvement strategy into other algorithm in algorithm execution, should be considered in further studies. AcknowledgmentThis work is jointly supported by the Young Fund of the Social Science of Ministry of Education of China (12YJC840005), the National Natural Science Foundation of China (71071128), and the Key Program of the National Social Science Foundation of China (12AZD110). [1]M.E.J.Newman, Fast algorithm for detecting community structure in networks.PhysicalReviewE, vol.69, no.6, pp.066133-066133, 2004. [2]M.Girvan and M.E.J.Newman, Community structure in social and biological networks,ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica, vol.99, no.12, pp.7821-7826, 2002. [3]S.Fortunatoand M.Barthélemy, Resolution limit in community detection,ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica, vol.104, no.1, pp.36-41, 2007. [4]Z.Li,S.Zhang, R.Wang,X.Zhang, and L.Chen,Quantitative function for community detection.PhysicalReviewE, vol.77, no.2, pp.257-260, 2008. [5]M.E.J.Newman, A.L.Barabàsi, and D.J.Watts, The Structure and Dynamic of Networks.New Jersey,USA:Princeton University Press, 2006. [6]F.Santo, Community detection in graphs,Physics, vol.486, no.3-5, pp.75-174, 2010. [7]S.White and P.Smyth, A Spectral Clustering Approach to Finding Communities in Graphs, inSIAMInternationalConferenceonDataMining, Newport Beach, California,USA, 2005. [8]C.Clauset, M.E.J.Newman, and C.Moore, Finding community structure in very large networks,PhysicalReviewE, vol.70, pp.264-277, 2004. [9]X.Wang, G.Chen, and H.Lu, A very fast algorithm for detecting community structures in complex networks.PhysicaA:StatisticalMechanicsanditsApplications, vol.384, no.2, pp.667-674, 2007. [10] V.D.Blondel, J.L.Guillaume, R.Lambiotte, and E.Lefebvre, Fast unfolding of communities in large networks.JournalofStatisticalMechanics:TheoryandExperiment, vol.2008, no.10, pp.155-168, 2008. [11] A.Medus, G.Acuna, and C.O.Dorso, Detection of community structures in networks via global optimization.PhysicaA:StatisticalMechanicsanditsApplications, vol.358, no.2-4, pp.593-604, 2005. [12] M.Tasgin, Community Detection Model using Genetic Algorithm in Complex Networks and Its Application in Real-Life Networks, MS Thesis, Graduate Program in Computer Engineering, Bogazici University, 2005. [13] O.D.Richard, E.H.Peter, and G.S.David,PatternClassification,SecondEdition.New York,USA: John Wiley & Sons, Inc, 2001. [14] U.Brandes, D.Delling, M.Gaertler, R.Goerke, M.Hoefer, Z.Nikoloski, and D.Wagner, Maximizing Modularity is hard,Physics, 2006. [15] F.Radicchi, C.Castellano, F.Cecconi, V.Loreto, and D.Parisi, Defining and identifying communities in networks.InProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica, USA, 2004, vol.101, no.9, pp.2658-2663. [16] A.Lancichinetti, S.Fortunato, and F.Radicchi, New benchmark in community detection.PhysicalReviewE, vol.78, no.4, pp.561-570, 2008. [17] L.Danon, A.Daz-Guilera, J.Duch, and A.Arenas, Comparing community structure identification.JournalofStatisticalMechanics:TheoryandExperiment, vol.2005, no.9, pp.09008, 2005. 2016-11-13; revised: 2016-12-07; accepted: 2016-12-08 •Wei Du and Xiaochen He are with the School of Public Policy and Administration, Center for Administration Complexity Science, Xi’an Jiaotong University, Xi’an 710049, China. E-mail:duwei@mail.xjtu.edu.cn; hexiaochen121vip@163.com *To whom correspondence should be addressed. Manuscript3 Experimental Results
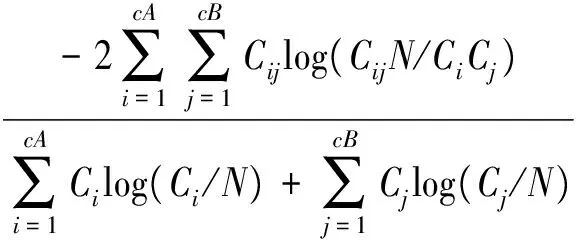



4 Conclusion
杂志排行
CAAI Transactions on Intelligence Technology的其它文章
- A Multi-Objective Evolutionary Approach to Selecting Security Solutions
- Fine-grained Image Categorization Based on Fisher Vector
- Second Order Differential Evolution Algorithm
- Change Detection in Synthetic Aperture Radar Images Based on Fuzzy Restricted Boltzmann Machine
- Automated Test Data Generation Based on Particle Swarm Optimization with Convergence Speed Controller
- Research on Micro-blog New Word Recognition Based on SVM
